21 января 2020 smart-lab.ru
Ещё до того как я познакомился с критерием Келли, я уже успел наработать собственную широкую базу риск-оценок. И вопрос отказа от этого критерия для меня был, по сути, риторическим, тем более, что Келли, как бы мы того не хотели, достаточно примитивный (упрощённый) критерий. Но прежде чем отказываться от критерия хорошо бы вообще понять что это такое, учитывая, что критерий представляет весьма простое решение сложной задачи и интересен именно этим.
Для примера возьмём игру с нулевым E, в которой выигрыши распределены равномерно, с вероятностью 50/50 и представлены множеством {+50%,-50%}. За некоторое количество повторений, например за два раунда, мы будем иметь следующее распределение финансового результата:
25% случаев — выигрыш 125% капитала до 2.25 (два выигрыша подряд)
25% случаев — проигрыш 75% капитала до 0.25 (два проигрыша подряд)
50% случаев — проигрыш 25% до 0.75 (один выигрыш и один проигрыш)
Рассчитав статистические моменты этого распределения легко убедиться, что средний выигрыш, как это положено, будет равен нулю, а наиболее вероятный вариант (мода) будет представлен проигрышем 25% капитала. Теперь, если варьировать ставку, можно убедиться, что с ростом ставки математическое ожидание по крайней мере не снижается, а мода, то есть наиболее вероятный исход — падает.
Проиллюстрируем этот эффект для сколь-либо длительной подобной игры:
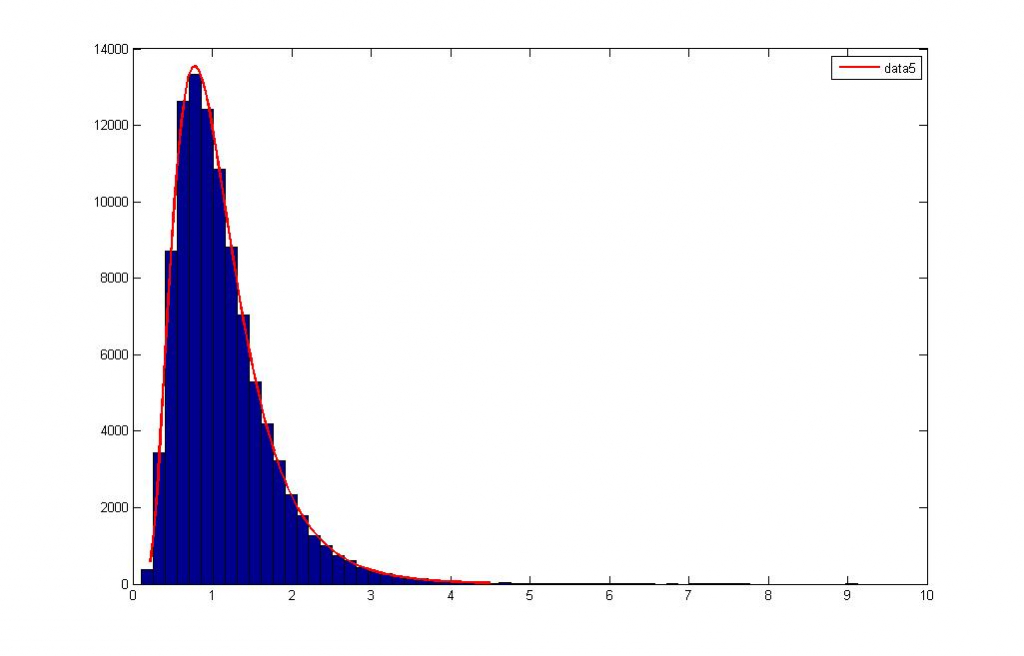
Иллюстрация — распределение результатов длительной игры с высокими рисками. По оси X — итоговый капитал к концу игры, по оси Y — абсолютная частота выпадения соответствующих событий.
Видно, что для высоких рисков любая игра постепенно превращается в лотерею, где частые закономерные убытки компенсируются редкими, но высокими прибылями. У распределения растёт скос, а вместе с ним и вероятность неудачи. Так, например, при ставках (выигрышах) в 100% данная игра превратиться в игру «пан или пропал» с 75% вероятностью полного, тотального разорения (достаточно одной неудачи) и 25% вероятностью ошеломительного успеха.
Выбирать стратегию ставок в данном случае мы можем несколькими способами:
Ограничение предела рисков/убытков — если, например, мы несем репутационные риски или имеем ограниченный капитал
Максимизацией прибыли за счёт использования максимально доступных плеч — если конкретные риски нам не важны
Максимизацией прибыли наиболее вероятного сценария, если предел убытка не ограничен, но ограничен капитал и его диверсификация.
Как известно, для подобного рода распределений (представляющих динамическое изменение ставок в соответствии с размером капитала), мода, то есть наиболее вероятный сценарий, достигает максимума при вариации параметров задачи одновременно с достижением максимума следующей величиной:
Который соответствует ставке K (в долях от капитала):
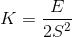
Продемонстрируем итоговое распределение для игр со ставкой, соответствующей Kелли/2 (максимум моды) и ставкой 2*Келли для игры 60/40 :
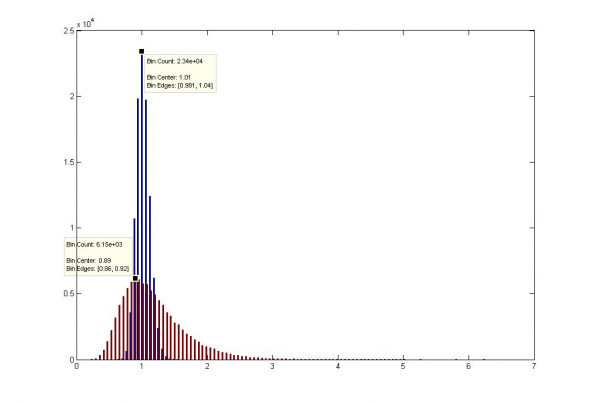
Иллюстрация — снижение моды и увеличение положительного скоса распределения при росте ставок. Келли/2 — синяя гистограмма, 2*Келли — красная.
Но если мы хотим ещё увеличить риски, но, при этом не допустить вырождения игры в «пан или пропал», сохранив её более-менее закономерный итог, то мы можем поставить другое ограничение :
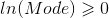
набирая риски до тех пор, пока пик распределения не уйдет в отрицательную зону, тогда:
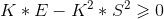

И эта задача уже полностью соответствует критерию Келли.
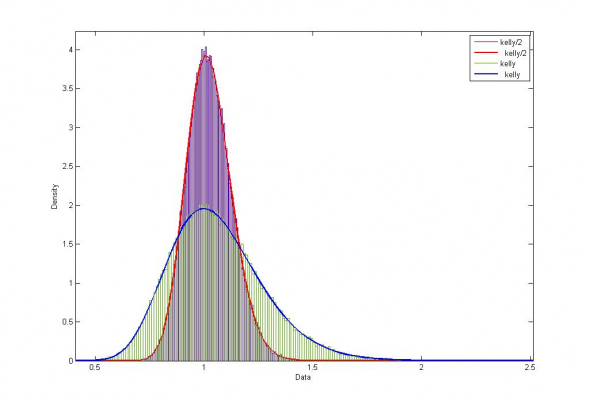
Иллюстрация — полученные распределения финансовых результатов игр для ставок Келли/2 (сиреневая гистограмма) и Келли (салатовая гистограмма).
Таким образом, что мы можем сказать о Келли?
Стратегии по Келли полностью игнорируют риски и не допускают динамического управления ими.
Связь ограничения рисков и ставок для стратегий Келли слабая (по сути, в неявном виде она опосредована через моду).
Стратегия Келли/2 представляет из себя более стабильный вариант, максимизирующий фин. результат наиболее вероятного сценария.
Стратегия Келли — предельный случай, граница ставок, сразу за которой игра превращается в лотерею.
Распространённые утверждения о падении ожидаемой доходности (матожидания) с ростом ставок, по крайней мере, сомнительны.
/ (C) Источник
Не является индивидуальной инвестиционной рекомендацией
При копировании ссылка обязательна Нашли ошибку: выделить и нажать Ctrl+Enter
Для примера возьмём игру с нулевым E, в которой выигрыши распределены равномерно, с вероятностью 50/50 и представлены множеством {+50%,-50%}. За некоторое количество повторений, например за два раунда, мы будем иметь следующее распределение финансового результата:
25% случаев — выигрыш 125% капитала до 2.25 (два выигрыша подряд)
25% случаев — проигрыш 75% капитала до 0.25 (два проигрыша подряд)
50% случаев — проигрыш 25% до 0.75 (один выигрыш и один проигрыш)
Рассчитав статистические моменты этого распределения легко убедиться, что средний выигрыш, как это положено, будет равен нулю, а наиболее вероятный вариант (мода) будет представлен проигрышем 25% капитала. Теперь, если варьировать ставку, можно убедиться, что с ростом ставки математическое ожидание по крайней мере не снижается, а мода, то есть наиболее вероятный исход — падает.
Проиллюстрируем этот эффект для сколь-либо длительной подобной игры:

Иллюстрация — распределение результатов длительной игры с высокими рисками. По оси X — итоговый капитал к концу игры, по оси Y — абсолютная частота выпадения соответствующих событий.
Видно, что для высоких рисков любая игра постепенно превращается в лотерею, где частые закономерные убытки компенсируются редкими, но высокими прибылями. У распределения растёт скос, а вместе с ним и вероятность неудачи. Так, например, при ставках (выигрышах) в 100% данная игра превратиться в игру «пан или пропал» с 75% вероятностью полного, тотального разорения (достаточно одной неудачи) и 25% вероятностью ошеломительного успеха.
Выбирать стратегию ставок в данном случае мы можем несколькими способами:
Ограничение предела рисков/убытков — если, например, мы несем репутационные риски или имеем ограниченный капитал
Максимизацией прибыли за счёт использования максимально доступных плеч — если конкретные риски нам не важны
Максимизацией прибыли наиболее вероятного сценария, если предел убытка не ограничен, но ограничен капитал и его диверсификация.
Как известно, для подобного рода распределений (представляющих динамическое изменение ставок в соответствии с размером капитала), мода, то есть наиболее вероятный сценарий, достигает максимума при вариации параметров задачи одновременно с достижением максимума следующей величиной:
[img]https://latex.codecogs.com/gif.latex?Max(Mode)&space;=&space;Max(E-S^2)[/img]
Который соответствует ставке K (в долях от капитала):
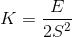
Продемонстрируем итоговое распределение для игр со ставкой, соответствующей Kелли/2 (максимум моды) и ставкой 2*Келли для игры 60/40 :

Иллюстрация — снижение моды и увеличение положительного скоса распределения при росте ставок. Келли/2 — синяя гистограмма, 2*Келли — красная.
Но если мы хотим ещё увеличить риски, но, при этом не допустить вырождения игры в «пан или пропал», сохранив её более-менее закономерный итог, то мы можем поставить другое ограничение :
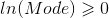
набирая риски до тех пор, пока пик распределения не уйдет в отрицательную зону, тогда:
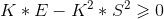

И эта задача уже полностью соответствует критерию Келли.

Иллюстрация — полученные распределения финансовых результатов игр для ставок Келли/2 (сиреневая гистограмма) и Келли (салатовая гистограмма).
Таким образом, что мы можем сказать о Келли?
Стратегии по Келли полностью игнорируют риски и не допускают динамического управления ими.
Связь ограничения рисков и ставок для стратегий Келли слабая (по сути, в неявном виде она опосредована через моду).
Стратегия Келли/2 представляет из себя более стабильный вариант, максимизирующий фин. результат наиболее вероятного сценария.
Стратегия Келли — предельный случай, граница ставок, сразу за которой игра превращается в лотерею.
Распространённые утверждения о падении ожидаемой доходности (матожидания) с ростом ставок, по крайней мере, сомнительны.
/ (C) Источник
Не является индивидуальной инвестиционной рекомендацией
При копировании ссылка обязательна Нашли ошибку: выделить и нажать Ctrl+Enter


