20 июля 2017 utmedia
Когда вы видите, что формируется определенная графическая модель, другие трейдеры тоже, вероятнее всего, ее заметят. Как же получить преимущество при торговле по графическим формациям? Попробуем разобраться в этой статье.
Большинство технических методов, включающих работу с графическими формациями, основаны на простом поиске торговых сигналов и не проходят строгого тестирования с точки зрения статистики. Все то, что мы читаем о графических формациях в интернете, книгах или журнальных статьях, является, в большинстве случаев, изложением личных наблюдений авторов, которые сумели подметить нечто, что они сочли ценным и достойным того, чтобы поделиться этой информацией с широкой общественностью.
Прежде чем рисковать деньгами на своем торговом счете, работая с любой графической формацией нужно задаться следующими вопросами: Давала ли исторически торговля данной формации преимущество? Каково арифметическое значение такого преимущества? Какое преимущество можно ожидать, исходя из исторических показателей данной формации? В чем разница между теоретическим преимуществом и реальным преимуществом, которое можно получить, торгуя по данной формации в реальном времени? Цель данной статьи - помочь вам найти ответы на эти вопросы.
Преимущество над другими игроками
В каком случае игру на удачу можно назвать "честной"? Короткий ответ звучит так: когда средний ожидаемый выигрыш для всех соперников в каждой игре равен нулю. Когда средний ожидаемый выигрыш в каждой игре для одного из игроков не равен нулю, можно считать, что у него есть преимущество (положительное или отрицательное) над другими игроками.
Упрощенно говоря, нам нужно от игры, чтобы, с одной стороны, она не была честной (в понимании приведенного определения), а с другой стороны - чтобы нам было позволено играть в нее, имея на своей стороне положительное преимущество.
В случае простой игры на удачу, где вероятности исходов известны, легко можно вычислить, имеет ли игрок преимущество, а также точное значение такого преимущества. Например, для рулетки с двойным нулем можно вычислить, что у игрока есть отрицательное преимущество в размере 5.26% (и, соответственно, у казино есть положительное преимущество 5.26%). Это означает, что, в среднем, для каждой ставки $x на колесе рулетки, казино может надеяться получить чистую прибыль в размере 5.26% от х$.
Приведу два примера без использования строгих математических формулировок, чтобы помочь вам понять начальную идею, которую мы впоследствии распространим на графические формации.
Пример 1: Игра с монеткой
Вам предлагается игра, в которой подбрасывается монетка, а вы делаете умозрительные ставки до подбрасывания. Умозрительная ставка (УС) - это база, на основании которой будут рассчитываться прибыль или убыток. Если выпадет решка, вы потеряете 1.2 УС (т. е. 1.2$ с каждого 1$ УС). Если выпадет орел, вы получите 2.3 УС (т. е. 2.3$ за каждый 1$ УС). Далее предположим, что вероятность выпадения орла составляет 50% (соответственно, вероятность выпадения решки - тоже 50%). Это означает, что сама по себе монетка является "честной", так как ни орел, ни решка не имеют преимущества.
Но будет ли такая игра с подбрасыванием монетки честной для вас? Вы можете надеяться, что после каждых двух подбрасываний, в среднем, будете получать один орел и одну решку. Если вы всегда будете ставить 1$, то на каждой решке будете терять 1.2$, а каждый орел будет приносить вам выигрыш 2.5$. Таким образом, после двух подбрасываний, вложив сумму 2$, вы получите чистую прибыль в размере 0.30$. Это означает, что такая игра, в среднем, все же не является честной, так как после каждых двух подбрасываний вы можете ожидать прибыль в размере 0.30$. Если разделить эту прибыль на сумму УС 2$, то получим 0.15 или 15%. Это - преимущество, которое имеет игрок в данной игре. С практической точки зрения, делая умозрительную ставку $x при каждом подбрасывании, вы можете рассчитывать на получение прибыли, в среднем, в размере 15% от х (т. е. 0.15x$) при каждом подбрасывании.
Пример 2: Игра с кубиками
В этой игре вы делаете свою условную ставку и бросаете кубик. Если на кубике выпадает 1 или 2, вы теряете деньги в размере УС. Но если выпадает 3 или больше, вы получаете 55% от УС. Есть ли у вас преимущество в данной игре? Предположим, что вы всегда делаете УС в размере 1$.
Тогда, в среднем, после шести бросков, можно ожидать, что выпадут разные грани кубика, и вы потеряете, в общей сложности, 2$ (по 1$ при выпадении 1 и 2), но заработаете 2.20$ (по 0.55$ за каждое выпадение 3, 4, 5, 6). Таким образом, в среднем, для каждых шести бросков, ваша суммарная ставка будет составлять 6$ (по 1$ за раз), а общая чистая прибыль - 0.20$ (2.20$-2.00$). Это означает, что данная игра также не является честной и дает вам преимущество. Чтобы вычислить это преимущество, нужно разделить чистую прибыль 0.20$ на сумму УС 6$, что даст примерно 0.0333 или 3.33%.
В приведенных примерах нам были известны точные вероятности исходов для монетки и кубика (вероятность выпадения 2 на кубике равна 1/6). Мы также знали уровень выплаты для каждого из исходов. Это позволяет легко вычислить преимущество. В случаях, когда мы не знаем ни вероятности исходов, ни выплаты на УС, нужно проводить моделирование по методу Монте-Карло при постоянной УС, чтобы рассчитать общую чистую прибыль, а затем - разделить ее на сумму УС, чтобы получить значение преимущества в такой игре. Когда мы говорим о графических формациях, имеются достаточные исторические данные, позволяющие оценить историческое преимущество определенной модели и вычислить значение такого преимущества.
Случай с графическими формациями
Чтобы рассчитать преимущество графической формации, нужно учитывать следующее:
Следует избегать нечеткого описания формации. Если формация определена нечетко, есть риск, что ваши решения по ней тоже будут нечеткими. Формации, которые могут находиться алгоритмически, компьютером, подходят лучше всего, так как они позволяют быстро и объективно собрать несколько случаев, пригодных для нашего исследования.
Нужно задавать определенное пороговое значение цены, которое будет служить сигналом о том, что модель не сработала так, как мы ожидали. Например, это может быть уровень стоп-лосс. Это важно для определения потерь, когда формация не срабатывает. (Например, для вершины в виде "голова и плечи", рост цены выше уровня головы обычно считается окончанием медвежьего смысла данной модели). Учитывая описание графических формаций с точки зрения технического анализа, и чтобы избежать конкретных проявлений преимущества одних формаций над другими, такой граничный уровень должен учитывать размеры формации, что облегчит принятие решений в целом и обеспечит единообразие оценки.
Необходимо иметь четкое определение того, чего вы ожидаете от формации (например, достижения целевого уровня цены). Если вы считаете, что формация должна привести к ценовому движению, но у него нет конкретной ценовой цели, нужно особое внимание уделить тому, каким должно быть это движение, и как оно определяется. Это позволит получить четкий метод единообразного расчета прибыли. Например, направленные движения легко можно описывать величиной коррекций. Любая коррекция, превышающая конкретное пороговое значение, автоматически будет говорить об окончании направленного движения.
Это, по сути, является рассмотрением формации в контексте определенной системы торговли. Именно так следует поступать, если вы хотите вычислить, имеет ли ваша система преимущество.
Вы предполагаете, что будете входить в рынок, когда выполняются конкретные условия, и выходить, когда также выполняются конкретные условия. Вам также заранее известно, сколько денег вы потеряете, если ваша формация не сработает. Определив цену входа, уровень стоп-лосса и то, как будет производиться расчет прибыли при торговле данной формации, можно провести тестирование на истории с использованием максимально большого количества случаев появления данной формации. Пусть P - это прибыль (положительная или отрицательная) от формации, определяемая как:
P = (Цена выхода - Цена входа) для сделок в лонг по формациям, которые считаются бычьими
P = (Цена входа - Цена выхода) для сделок в шорт по формациям, которые считаются медвежьими.
Пусть S - это удаленность стоп-лосса от цены входа:
S = | Цена входа - Уровень стоп-лосса |
(где | ? | обозначает модуль - абсолютное значение).
Тогда дробь:
PF = P/S
- это прибыль (в долларовом выражении) от формации, если вы торгуете по ней, используя умозрительную ставку в размере 1$ в каждой сделке. Это обеспечивает такую же нормализацию, как и постоянный размер умозрительной ставки 1$ в рассмотренных выше примерах с монеткой и кубиком.
Учтите, что если цена задевает стоп-лосс, и вы выходите из сделки точно на его уровне, то PF всегда будет больше или равен -1. Но если ваш выход на основании стоп-лосса заранее не определен (например, если цена проходит стоп-лосс с гэпом, что случается в реальных условиях, или когда вы считаете, что для подтверждения несрабатывания формации цена должна пройти дальше стопового уровня), тогда S и PF могут быть меньше -1. Учтите также, что PF практически играет роль коэффициента прибыли (отсюда и название PF - profit factor), так как, если ваша умозрительная ставка равна А$, когда достигается стоп-лосс, то прибыль будет в PF раз больше, чем А$.
Простое арифметическое среднее значений PF по всем историческим формациям отражает предполагаемое историческое преимущество для данной формации на основании тестирования на истории.
Преимущество графической формации "чашка"
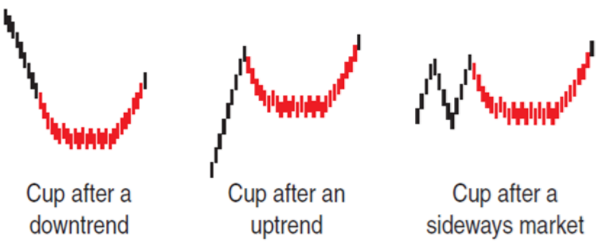
Этот пример я презентовал на конференции Международной федерации технического анализа IFTA в 2014 году в контексте более широкой темы, чтобы указать на достоинства алгоритмической идентификации графических формаций. Идеи, содержащиеся в данном примере, вы можете применить к формациям, которые захотите исследовать. Я рассматривал "чашку", которая представляет собой закругляющуюся базу или закругляющееся дно, которое возникает после нисходящего тренда (рисунок 1).
Рисунок 1. Примеры «чашки» (закругляющееся дно)
В целом, считается, что "чашка" имеет бычьи последствия для движения цены. Хотя важно, как ведут себя объемы во время формирования "чашки", а сама формация имеет много разновидностей (например, "чашка с ручкой"), для простоты я решил не учитывать в своем исследовании объемы и разновидности, а сосредоточиться на последствиях данной ценовой формации. В своей презентации на IFTA я использовал немного видоизмененный алгоритм идентификации "чашки", который представил в своих статьях еще в 2006 году.
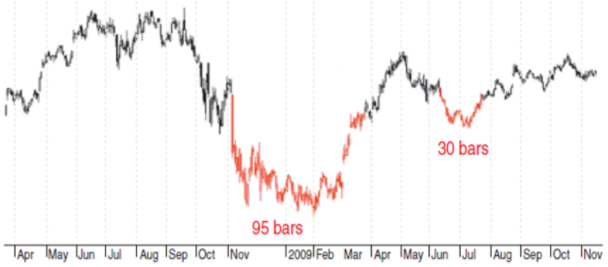
Я использовал дневные графики акций, входящих в S&P 500, за период с 1982 по 2014 годы, где нашел, в общей сложности, 3991 четкую "чашку" различной продолжительности (под "четкой" я подразумеваю, что пересечение по времени любых двух "чашек" на одном графике не превышало 70%). На рисунке 2 показаны примеры "чашек", найденных данным алгоритмом на дневном графике.
Рисунок 2. «Чашки» на дневном графике
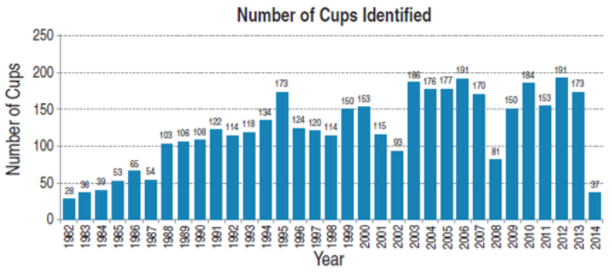
На рисунке 3 вы видите количество выявленных "чашек" с разбивкой по годам, а на рисунке 4 - процент частоты встречаемости длительности "чашек".
Рисунок 3. Количество найденных чашек по годам
Рисунок 4. Диаграмма частотного распределения длительности чашек
Почти половина (46%) всех чашек имели длительность от 20 до 30 дней
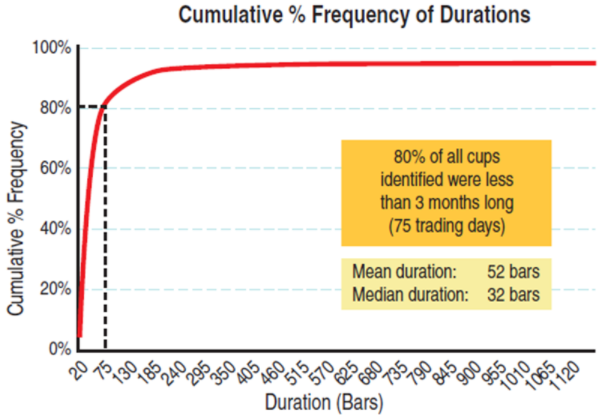
Минимальная длительность составила 20 баров, а максимальная - 1162 бара. Средняя длительность составила 32 бара, а 80% всех найденных "чашек" имели длительность не более 75 баров (см. рисунок 5).
Рисунок 5. Кумулятивная диаграмма частотного распределения «чашек» по длительности
Вот как я определял стоп-лосс для "чашек". Пусть Н - это High бара идентификации (High бара, на котором идентифицируется "чашка"), а L - самый нижний Low в "чашке". Тогда высота от H до L в процентном отношении составляет:
(H - L)/Hx100%
Величина стоп-лосса в этом случае задается как 0.7 от этой высоты в процентах. Так, например (см. рисунок 6), если H = 200, а L = 140, то высота от H до L в процентном отношении составляет 30%. 0.7 от 30% равно 21%. Поэтому уровень стоп-лосса - на 21% ниже цены входа (200), то есть - 158.
Рисунок 6. Установка начального стоп-лосса
Поскольку считается, что формация "чашка" приводит к движению цены вверх, а стандартной ценовой цели для нее не существует, я предположил, что моя система торговли работает только на покупку, открывая сделки на уровне High бара идентификации с подтягиванием начального стопа (следящий стоп). Выход из сделки производится только по срабатыванию стопового ордера. Обратите внимание, что следящий стоп естественным образом связан с высотой "чашки" в процентном отношении, чтобы обеспечить единообразие анализа всех "чашек".
Почему я использовал значение 0.7 в качестве коэффициента для начального стопа, а не 0.5, 0.8 или 1? Особого смысла в этом нет. Это просто пример. Так как начальный стоп впоследствии становится следящим, то применение разных значений этого коэффициента приведет к анализу бычьих последствий данной формации с разных точек зрения. Если быть более точным, значение этого коэффициента определяет величину коррекции, которую вы допускаете при бычьем движении. Например, установив значение 0.2, вы можете проанализировать, порождают ли "чашки" мгновенные и сильные тренды (небольшие, по отношению к высоте "чашки" в процентах, коррекции). Значение 0.7, как мне показалось, хорошо соответствовало общей идее, так как давало достаточно, но не слишком много, пространства для коррекций. Никто не мешает вам исследовать разные значения этого коэффициента, чтобы выяснить, какое из них приводит к наилучшим результатам. Чтобы определить прибыль/убыток, я принимал в расчет гэпы, приводящие к проскакиванию ценой уровня следящего стопа. Я также установил требование, что следящий стоп должен пройти через цену закрытия, чтобы служить сигналом к выходу. В качестве значения для выхода я использовал Low бара выхода (чтобы учесть проскальзывание), поэтому PF мог принимать значения меньше -1.
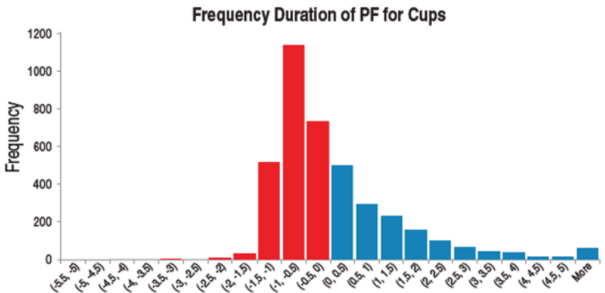
Диаграмма распределения PF для всех "чашек" приведена на рисунке 7. Среднее значение составляет 0.166, или 16.6%, и это - историческое преимущество формации "чашка" за период с 1982 по 2014 год. Прошу заметить, что это - с точки зрения системы, которая использовалась для оценки бычьих последствий данной формации.
Эти результаты интересны тем, что, согласно им, на каждый 1$, который вы поставили бы на бычьи последствия формации "чашка", можно было бы получить, в среднем, 0.16$ прибыли.
Интересно также, что только 39% сделок по этой системе были прибыльными. Это означает, что было много убытков, но маленьких; а прибыльных сделок было меньше, чем убыточных, но они были достаточно крупными (рисунок 7). Этого и следовало ожидать, так как применение начального стопа предотвращало появление крупных убытков, а следящий стоп позволял прибыли расти.
Рисунок 7. Диаграмма частотного распределения PF «чашек» за период с 1982 по 2014 год
Если количество исторических PF достаточно большое, а распределение PF не слишком отличается от нормального распределения, то можно применить статистический тест, носящий название "параметрический t-критерий Стьюдента" (это практически то же самое, что и статистический z-тест для крупных выборок), чтобы вычислить так называемый "доверительный интервал" для математического ожидания PF (то есть доверительный интервал для преимущества для всех "чашек"). Например, предполагая, что использованная в данном исследовании историческая выборка 3991 "чашки" является не субъективной выборкой из всего множества "чашек" (так как период времени с 1982 по 2014 год достаточно длительный и охватывает разные рыночные условия), тест Стьюдента показал, что доверительный интервал для общего преимущества формации "чашка" - от 9.1% до 24% с доверием 99%. Другими словами, расчетные значения исторических PF свидетельствуют, что есть 99% уверенности в том, что истинное преимущество "чашки" как бычьей формации находится в пределах от 9.1% до 24%.
Большинство технических методов, включающих работу с графическими формациями, основаны на простом поиске торговых сигналов и не проходят строгого тестирования с точки зрения статистики. Все то, что мы читаем о графических формациях в интернете, книгах или журнальных статьях, является, в большинстве случаев, изложением личных наблюдений авторов, которые сумели подметить нечто, что они сочли ценным и достойным того, чтобы поделиться этой информацией с широкой общественностью.
Прежде чем рисковать деньгами на своем торговом счете, работая с любой графической формацией нужно задаться следующими вопросами: Давала ли исторически торговля данной формации преимущество? Каково арифметическое значение такого преимущества? Какое преимущество можно ожидать, исходя из исторических показателей данной формации? В чем разница между теоретическим преимуществом и реальным преимуществом, которое можно получить, торгуя по данной формации в реальном времени? Цель данной статьи - помочь вам найти ответы на эти вопросы.
Преимущество над другими игроками
В каком случае игру на удачу можно назвать "честной"? Короткий ответ звучит так: когда средний ожидаемый выигрыш для всех соперников в каждой игре равен нулю. Когда средний ожидаемый выигрыш в каждой игре для одного из игроков не равен нулю, можно считать, что у него есть преимущество (положительное или отрицательное) над другими игроками.
Упрощенно говоря, нам нужно от игры, чтобы, с одной стороны, она не была честной (в понимании приведенного определения), а с другой стороны - чтобы нам было позволено играть в нее, имея на своей стороне положительное преимущество.
В случае простой игры на удачу, где вероятности исходов известны, легко можно вычислить, имеет ли игрок преимущество, а также точное значение такого преимущества. Например, для рулетки с двойным нулем можно вычислить, что у игрока есть отрицательное преимущество в размере 5.26% (и, соответственно, у казино есть положительное преимущество 5.26%). Это означает, что, в среднем, для каждой ставки $x на колесе рулетки, казино может надеяться получить чистую прибыль в размере 5.26% от х$.
Приведу два примера без использования строгих математических формулировок, чтобы помочь вам понять начальную идею, которую мы впоследствии распространим на графические формации.
Пример 1: Игра с монеткой
Вам предлагается игра, в которой подбрасывается монетка, а вы делаете умозрительные ставки до подбрасывания. Умозрительная ставка (УС) - это база, на основании которой будут рассчитываться прибыль или убыток. Если выпадет решка, вы потеряете 1.2 УС (т. е. 1.2$ с каждого 1$ УС). Если выпадет орел, вы получите 2.3 УС (т. е. 2.3$ за каждый 1$ УС). Далее предположим, что вероятность выпадения орла составляет 50% (соответственно, вероятность выпадения решки - тоже 50%). Это означает, что сама по себе монетка является "честной", так как ни орел, ни решка не имеют преимущества.
Но будет ли такая игра с подбрасыванием монетки честной для вас? Вы можете надеяться, что после каждых двух подбрасываний, в среднем, будете получать один орел и одну решку. Если вы всегда будете ставить 1$, то на каждой решке будете терять 1.2$, а каждый орел будет приносить вам выигрыш 2.5$. Таким образом, после двух подбрасываний, вложив сумму 2$, вы получите чистую прибыль в размере 0.30$. Это означает, что такая игра, в среднем, все же не является честной, так как после каждых двух подбрасываний вы можете ожидать прибыль в размере 0.30$. Если разделить эту прибыль на сумму УС 2$, то получим 0.15 или 15%. Это - преимущество, которое имеет игрок в данной игре. С практической точки зрения, делая умозрительную ставку $x при каждом подбрасывании, вы можете рассчитывать на получение прибыли, в среднем, в размере 15% от х (т. е. 0.15x$) при каждом подбрасывании.
Пример 2: Игра с кубиками
В этой игре вы делаете свою условную ставку и бросаете кубик. Если на кубике выпадает 1 или 2, вы теряете деньги в размере УС. Но если выпадает 3 или больше, вы получаете 55% от УС. Есть ли у вас преимущество в данной игре? Предположим, что вы всегда делаете УС в размере 1$.
Тогда, в среднем, после шести бросков, можно ожидать, что выпадут разные грани кубика, и вы потеряете, в общей сложности, 2$ (по 1$ при выпадении 1 и 2), но заработаете 2.20$ (по 0.55$ за каждое выпадение 3, 4, 5, 6). Таким образом, в среднем, для каждых шести бросков, ваша суммарная ставка будет составлять 6$ (по 1$ за раз), а общая чистая прибыль - 0.20$ (2.20$-2.00$). Это означает, что данная игра также не является честной и дает вам преимущество. Чтобы вычислить это преимущество, нужно разделить чистую прибыль 0.20$ на сумму УС 6$, что даст примерно 0.0333 или 3.33%.
В приведенных примерах нам были известны точные вероятности исходов для монетки и кубика (вероятность выпадения 2 на кубике равна 1/6). Мы также знали уровень выплаты для каждого из исходов. Это позволяет легко вычислить преимущество. В случаях, когда мы не знаем ни вероятности исходов, ни выплаты на УС, нужно проводить моделирование по методу Монте-Карло при постоянной УС, чтобы рассчитать общую чистую прибыль, а затем - разделить ее на сумму УС, чтобы получить значение преимущества в такой игре. Когда мы говорим о графических формациях, имеются достаточные исторические данные, позволяющие оценить историческое преимущество определенной модели и вычислить значение такого преимущества.
Случай с графическими формациями
Чтобы рассчитать преимущество графической формации, нужно учитывать следующее:
Следует избегать нечеткого описания формации. Если формация определена нечетко, есть риск, что ваши решения по ней тоже будут нечеткими. Формации, которые могут находиться алгоритмически, компьютером, подходят лучше всего, так как они позволяют быстро и объективно собрать несколько случаев, пригодных для нашего исследования.
Нужно задавать определенное пороговое значение цены, которое будет служить сигналом о том, что модель не сработала так, как мы ожидали. Например, это может быть уровень стоп-лосс. Это важно для определения потерь, когда формация не срабатывает. (Например, для вершины в виде "голова и плечи", рост цены выше уровня головы обычно считается окончанием медвежьего смысла данной модели). Учитывая описание графических формаций с точки зрения технического анализа, и чтобы избежать конкретных проявлений преимущества одних формаций над другими, такой граничный уровень должен учитывать размеры формации, что облегчит принятие решений в целом и обеспечит единообразие оценки.
Необходимо иметь четкое определение того, чего вы ожидаете от формации (например, достижения целевого уровня цены). Если вы считаете, что формация должна привести к ценовому движению, но у него нет конкретной ценовой цели, нужно особое внимание уделить тому, каким должно быть это движение, и как оно определяется. Это позволит получить четкий метод единообразного расчета прибыли. Например, направленные движения легко можно описывать величиной коррекций. Любая коррекция, превышающая конкретное пороговое значение, автоматически будет говорить об окончании направленного движения.
Это, по сути, является рассмотрением формации в контексте определенной системы торговли. Именно так следует поступать, если вы хотите вычислить, имеет ли ваша система преимущество.
Вы предполагаете, что будете входить в рынок, когда выполняются конкретные условия, и выходить, когда также выполняются конкретные условия. Вам также заранее известно, сколько денег вы потеряете, если ваша формация не сработает. Определив цену входа, уровень стоп-лосса и то, как будет производиться расчет прибыли при торговле данной формации, можно провести тестирование на истории с использованием максимально большого количества случаев появления данной формации. Пусть P - это прибыль (положительная или отрицательная) от формации, определяемая как:
P = (Цена выхода - Цена входа) для сделок в лонг по формациям, которые считаются бычьими
P = (Цена входа - Цена выхода) для сделок в шорт по формациям, которые считаются медвежьими.
Пусть S - это удаленность стоп-лосса от цены входа:
S = | Цена входа - Уровень стоп-лосса |
(где | ? | обозначает модуль - абсолютное значение).
Тогда дробь:
PF = P/S
- это прибыль (в долларовом выражении) от формации, если вы торгуете по ней, используя умозрительную ставку в размере 1$ в каждой сделке. Это обеспечивает такую же нормализацию, как и постоянный размер умозрительной ставки 1$ в рассмотренных выше примерах с монеткой и кубиком.
Учтите, что если цена задевает стоп-лосс, и вы выходите из сделки точно на его уровне, то PF всегда будет больше или равен -1. Но если ваш выход на основании стоп-лосса заранее не определен (например, если цена проходит стоп-лосс с гэпом, что случается в реальных условиях, или когда вы считаете, что для подтверждения несрабатывания формации цена должна пройти дальше стопового уровня), тогда S и PF могут быть меньше -1. Учтите также, что PF практически играет роль коэффициента прибыли (отсюда и название PF - profit factor), так как, если ваша умозрительная ставка равна А$, когда достигается стоп-лосс, то прибыль будет в PF раз больше, чем А$.
Простое арифметическое среднее значений PF по всем историческим формациям отражает предполагаемое историческое преимущество для данной формации на основании тестирования на истории.
Преимущество графической формации "чашка"
Этот пример я презентовал на конференции Международной федерации технического анализа IFTA в 2014 году в контексте более широкой темы, чтобы указать на достоинства алгоритмической идентификации графических формаций. Идеи, содержащиеся в данном примере, вы можете применить к формациям, которые захотите исследовать. Я рассматривал "чашку", которая представляет собой закругляющуюся базу или закругляющееся дно, которое возникает после нисходящего тренда (рисунок 1).
Рисунок 1. Примеры «чашки» (закругляющееся дно)
В целом, считается, что "чашка" имеет бычьи последствия для движения цены. Хотя важно, как ведут себя объемы во время формирования "чашки", а сама формация имеет много разновидностей (например, "чашка с ручкой"), для простоты я решил не учитывать в своем исследовании объемы и разновидности, а сосредоточиться на последствиях данной ценовой формации. В своей презентации на IFTA я использовал немного видоизмененный алгоритм идентификации "чашки", который представил в своих статьях еще в 2006 году.
Я использовал дневные графики акций, входящих в S&P 500, за период с 1982 по 2014 годы, где нашел, в общей сложности, 3991 четкую "чашку" различной продолжительности (под "четкой" я подразумеваю, что пересечение по времени любых двух "чашек" на одном графике не превышало 70%). На рисунке 2 показаны примеры "чашек", найденных данным алгоритмом на дневном графике.
Рисунок 2. «Чашки» на дневном графике
На рисунке 3 вы видите количество выявленных "чашек" с разбивкой по годам, а на рисунке 4 - процент частоты встречаемости длительности "чашек".
Рисунок 3. Количество найденных чашек по годам
Рисунок 4. Диаграмма частотного распределения длительности чашек
Почти половина (46%) всех чашек имели длительность от 20 до 30 дней
Минимальная длительность составила 20 баров, а максимальная - 1162 бара. Средняя длительность составила 32 бара, а 80% всех найденных "чашек" имели длительность не более 75 баров (см. рисунок 5).
Рисунок 5. Кумулятивная диаграмма частотного распределения «чашек» по длительности
Вот как я определял стоп-лосс для "чашек". Пусть Н - это High бара идентификации (High бара, на котором идентифицируется "чашка"), а L - самый нижний Low в "чашке". Тогда высота от H до L в процентном отношении составляет:
(H - L)/Hx100%
Величина стоп-лосса в этом случае задается как 0.7 от этой высоты в процентах. Так, например (см. рисунок 6), если H = 200, а L = 140, то высота от H до L в процентном отношении составляет 30%. 0.7 от 30% равно 21%. Поэтому уровень стоп-лосса - на 21% ниже цены входа (200), то есть - 158.
Рисунок 6. Установка начального стоп-лосса
Поскольку считается, что формация "чашка" приводит к движению цены вверх, а стандартной ценовой цели для нее не существует, я предположил, что моя система торговли работает только на покупку, открывая сделки на уровне High бара идентификации с подтягиванием начального стопа (следящий стоп). Выход из сделки производится только по срабатыванию стопового ордера. Обратите внимание, что следящий стоп естественным образом связан с высотой "чашки" в процентном отношении, чтобы обеспечить единообразие анализа всех "чашек".
Почему я использовал значение 0.7 в качестве коэффициента для начального стопа, а не 0.5, 0.8 или 1? Особого смысла в этом нет. Это просто пример. Так как начальный стоп впоследствии становится следящим, то применение разных значений этого коэффициента приведет к анализу бычьих последствий данной формации с разных точек зрения. Если быть более точным, значение этого коэффициента определяет величину коррекции, которую вы допускаете при бычьем движении. Например, установив значение 0.2, вы можете проанализировать, порождают ли "чашки" мгновенные и сильные тренды (небольшие, по отношению к высоте "чашки" в процентах, коррекции). Значение 0.7, как мне показалось, хорошо соответствовало общей идее, так как давало достаточно, но не слишком много, пространства для коррекций. Никто не мешает вам исследовать разные значения этого коэффициента, чтобы выяснить, какое из них приводит к наилучшим результатам. Чтобы определить прибыль/убыток, я принимал в расчет гэпы, приводящие к проскакиванию ценой уровня следящего стопа. Я также установил требование, что следящий стоп должен пройти через цену закрытия, чтобы служить сигналом к выходу. В качестве значения для выхода я использовал Low бара выхода (чтобы учесть проскальзывание), поэтому PF мог принимать значения меньше -1.
Диаграмма распределения PF для всех "чашек" приведена на рисунке 7. Среднее значение составляет 0.166, или 16.6%, и это - историческое преимущество формации "чашка" за период с 1982 по 2014 год. Прошу заметить, что это - с точки зрения системы, которая использовалась для оценки бычьих последствий данной формации.
Эти результаты интересны тем, что, согласно им, на каждый 1$, который вы поставили бы на бычьи последствия формации "чашка", можно было бы получить, в среднем, 0.16$ прибыли.
Интересно также, что только 39% сделок по этой системе были прибыльными. Это означает, что было много убытков, но маленьких; а прибыльных сделок было меньше, чем убыточных, но они были достаточно крупными (рисунок 7). Этого и следовало ожидать, так как применение начального стопа предотвращало появление крупных убытков, а следящий стоп позволял прибыли расти.
Рисунок 7. Диаграмма частотного распределения PF «чашек» за период с 1982 по 2014 год
Если количество исторических PF достаточно большое, а распределение PF не слишком отличается от нормального распределения, то можно применить статистический тест, носящий название "параметрический t-критерий Стьюдента" (это практически то же самое, что и статистический z-тест для крупных выборок), чтобы вычислить так называемый "доверительный интервал" для математического ожидания PF (то есть доверительный интервал для преимущества для всех "чашек"). Например, предполагая, что использованная в данном исследовании историческая выборка 3991 "чашки" является не субъективной выборкой из всего множества "чашек" (так как период времени с 1982 по 2014 год достаточно длительный и охватывает разные рыночные условия), тест Стьюдента показал, что доверительный интервал для общего преимущества формации "чашка" - от 9.1% до 24% с доверием 99%. Другими словами, расчетные значения исторических PF свидетельствуют, что есть 99% уверенности в том, что истинное преимущество "чашки" как бычьей формации находится в пределах от 9.1% до 24%.
Не является индивидуальной инвестиционной рекомендацией | При копировании ссылка обязательна | Нашли ошибку - выделить и нажать Ctrl+Enter | Жалоба