1 октября 2017 Trade Like A Pro
Среди множества различных информационных источников порой довольно трудно найти необходимую информацию и собрать ее в единое целое. Связано это по большей части с тем, что большинство авторов книг, статей и курсов по трейдингу – люди, далекие от математики. Поэтому многие вещи описываются поверхностно, некоторые моменты трактуются вообще неверно. Вторая проблема заключается в том, что многие любители Форекс также люди, глубоко не разбирающиеся в этой самой математике, а некоторые нюансы того же мани менеджмента было бы сложно понять, не углубляясь в дебри формул.
Сегодня мы с вами разберем, что же такое критерий Келли и как его применять на рынке без сложных формул и математических терминов. Все выводы и доказательства, исследования, теоремы и прочие сложности — будут опущены, а вместо этого я расскажу о самих результатах всех страшных вышеперечисленных вещей простым и понятным языком.
История критерия Келли
Как и стратегии Д‘Аламбера с Мартингейлом, критерий Келли известен любителям ставок на спорт уже много лет. Проблему оптимальной ставки пытаются решить еще с восемнадцатого столетия, с обсуждения Даниилом Бернулли Санкт-Петербургского Парадокса. Даже в этом вопросе точки зрения разделились – одни пытаются минимизировать вероятность потерять весь депозит за определенное количество будущих сделок, другие же, наоборот, хотят за это количество сделок получить максимально возможный прирост. Еще один подход состоит в том, чтобы оценить деньги, используя функцию полезности. Иными словами, все сводится к тому, чтобы максимально полезно использовать свой депозит. Даниил Бернулли в 18 веке использовал функцию полезности при попытке решения Санкт-Петербургского Парадокса, но безуспешно.
О формуле вспомнил Джон Ларри Келли в 1956 году, заметив ее некоторые интересные свойства. В то время он работал на фирму AT&T Bell Laboratories, занимающуюся телекоммуникациями, электронными и компьютерными системами. Строго говоря, эта формула была им применена именно в этой сфере. Затем, пятью годами позже эти свойства были изучены и обобщены в исследовании Бримана. Ну а уже Марковиц в том же году решил применить формулу к ценным бумагам. А спустя еще год, в 1962 году, Эдвард О. Торп подробно описал критерий в первом издании своей книги Beat the Dealer («Побить дилера»). Такая вот нелегкая история у этого критерия, названного не в честь реального автора и получившего распространение на финансовых рынках также по воле совсем другого человека.
Что такое критерий Келли и как его рассчитать?
Критерий Келли обладает рядом свойств для заданной торговой системы с положительным математическим ожиданием и вот самые «волшебные» из них:
размер капитала неограниченно растет;
вероятность разорения игрока стремится к нулю при увеличении числа трейдов.
И действительно, при применении критерия Келли капитал будет расти быстрее, чем при применении любого другого метода управления средствами. На самом деле, определяя размер лота по этому методу, трейдер действует оптимально, но только в очень частном случае. Под самой оптимальностью тут понимается вот что:
максимально быстрое достижение капиталом заранее заданной величины;
достижение максимальной величины капитала после фиксированного числа сделок.
Пахнет разгоном, не так ли? Совершенно верно, и немного позже вы поймете, почему.
А для начала давайте разберемся с формулой критерия Келли. В литературе можно найти огромное количество различных формул для расчета, и все они будут верны. В сети встречается очень много вариантов формул для беттинга, которые также авторы статей пытаются применить к финансовым рынкам. Самая общая из встреченных мной формул выглядит так:
X = p – q/w, где:
p – вероятность выигрыша;
q – вероятность проигрыша;
w – средняя величина выигрыша (также часто рекомендуют использовать среднюю величину выигрыша относительно среднего проигрыша).
Исходя из формулы, вы всегда должны ставить в каждой сделке x от размера вашего капитала. То есть если x = 0.1, то при каждой сделке нужно ставить 10% от вашего капитала. Приведенную выше формулу далее давайте будем называть «простым» критерием Келли.
Если TAKE PROFIT = STOP LOSS, т.е. W=1, формула упрощается до: F = P(W) — P(L).
Таким образом, если вероятность выигрыша составляет 60%, то F=20%.
Давайте попробуем применить критерий Келли, высчитанный по такой формуле, к системе со стопом, тремя уровнями тейкпрофита, безубытком, двумя различными видами трейлинг стопа и выходом по стохастику:
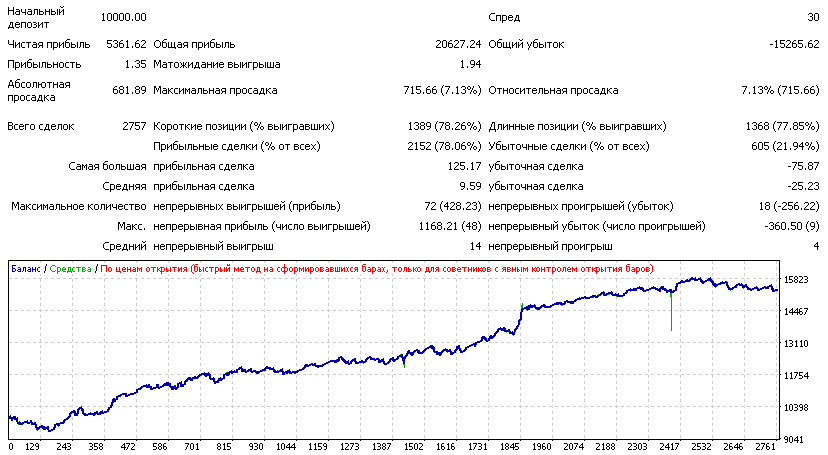
Система имеет 78.06% прибыльных сделок со средней прибылью 9.59$ и средним убытком -25,23$.
Давайте перенесем статистику в Excel, чтобы дальше производить наши вычисления. Построим график прироста депозита фиксированным лотом 0.1:
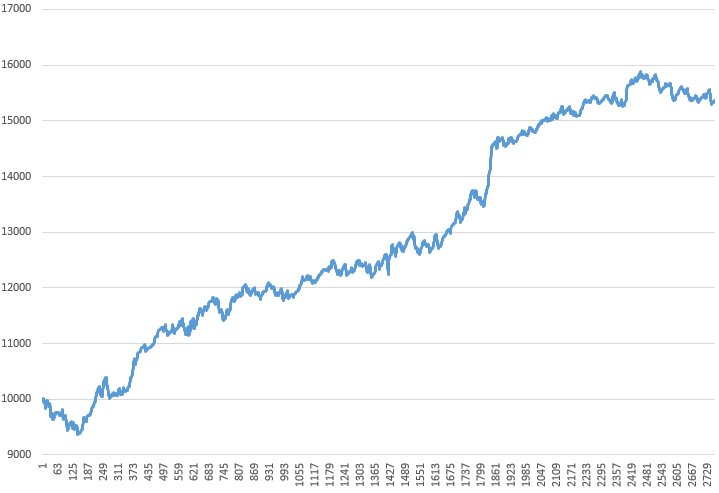
Теперь рассчитаем для нашей системы критерий Келли по формуле X = p – q/w:
Х = 78,06 – 21,94/(9,59/25,23) = 20,32%.
Соответствующий график:
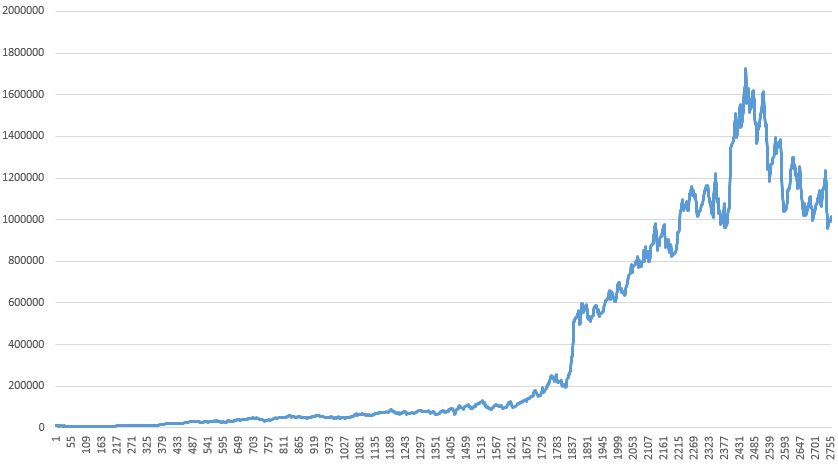
Наш депозит показал пик на отметке 1 724 000, а затем мы попали в серию неудачных сделок, что снизило наш баланс до 997 000.
Оптимальность критерия Келли
Относительная скорость роста капитала в зависимости от выбранного плеча будет пропорциональна k-0.5*k^2, где k — критерий Келли. Первое слагаемое понятно — в первом приближении скорость должна быть пропорциональна плечу, так вроде бы и следует из здравого смысла. Второе слагаемое описывает убыток пересчета, который при небольших плечах практически незаметен, но быстро увеличивается с ростом плеча и после Келли жестко убивает доходность в ноль — территория больших критериев заканчивается «ямой для особо жадных».

С увеличением плеча прибыль растет линейно, а убыток пересчета, как видно из формулы, нарастает квадратично. Это приводит к тому, что с увеличением плеча общая доходность торговли растет все меньше и меньше, а после достижения некоторого оптимума начинает падать и вскоре уходит в минус. Получается странная вещь – имеем, к примеру, довольно неплохую стратегию с множеством прибыльных сделок, принимаем решение поднять плечо до максимума с целью выжать побольше дохода, и в результате неожиданно получаем полную потерю счета.
Скорость роста достигает оптимума при значении плеча Nk, соответствующему критерию Келли, и с дальнейшим повышением плеча начинает снижаться, быстро достигая нуля и уходя в отрицательную зону для избыточно больших плеч («яма для жадных»). Теперь должно быть понятно, что есть оптимальное плечо, на котором мы имеем максимальную доходность, и выше которого убыток пересчета начитает убивать прибыль. С увеличением плеча выше оптимального, несмотря на растущую волатильность счета, итоговая прибыль становится все меньше и меньше.
Выходит, нельзя повышать плечо, не зная заранее его оптимальный по Келли уровень для используемой стратегии. Результаты могут неприятно удивить. Выше критерия Келли следует обрыв доходности вниз, можно влететь в него и попасть в «яму для жадных». Именно поэтому не стоит использовать полученный критерий без искусственного уменьшения.
Ограничения стандартной формулы
Почти нигде не написано, что в такой формулировке критерий Келли предполагает, что в торговой системе могут быть только результаты:
-1хСтавка (то есть трейдер проигрывает при х=0.1 ровно 10% от депозита);
+ wхСтавка (то есть или выигрыш w, или проигрыш -1).
Такой вариант, как вы видите, довольно частный случай, в котором исхода у сделки может быть только два – либо стоп лосс, либо тейк профит. А вот более обобщенный вариант, где возможно большое число различных результатов каждой сделки (например, в системах с применением безубытка, трейлинг стопа и выхода по системе), такой вариант расчета не подойдет.
Поэтому необходимо обобщить формулу расчета критерия Келли. Опуская теоретические выкладки, доказательства и формулировки, я приведу лишь конечный результат.
Обобщенная формула критерия Келли
Пусть у нас есть торговая система, которая дала следующие результаты {ai,ki} при i=0…n, где k – количество сделок с одним результатом, a – их результат, i – количество сделок. Чтобы было понятнее: мы совершили по системе кучу сделок и разбили эти сделки по результатам. Получилось у нас, например, 10 сделок по бу (0%), 30 сделок с профитом 2%, 20 сделок с убытком -3% и так далее. Таких вариантов у нас может быть сколько угодно много, их i штук. В каждом таком наборе у нас количество сделок с одним результатом (k) и сам результат (a). Если a>0, то сделка или сделки закрылись с прибылью, если a<0, то с убытком.
Сделки с нулевым результатом можно отбросить, на конечный результат системы они не влияют. Теперь будем считать, что все сделки (или кучки сделок с одинаковыми результатами) у нас упорядочены по возрастанию, при этом у нас есть хотя бы одна кучка убыточных сделок, то есть a1 0. А случается такое, когда математические ожидание системы положительно. Если сумма всех aiki меньше либо равно нулю, система обречена на слив и никакая система управления капиталом тут не поможет.
Введем функцию:
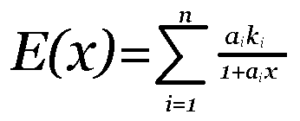
Известно, что существует и единственно 01, то, ставя x, трейдер пришел к успеху.
И последний пункт, касающийся скорее сравнения двух систем. Пусть у нас есть две системы {a1i,k1i} и {a2i,k2i} с положительным математическим ожиданием, которые были испытаны на одинаковом интервале времени. Первая система сделала i1 сделок, вторая i2 сделок, трейдер ставил в первой системе х1, во второй х2. Тогда первая система будет эффективней второй, если G1(x1,i1)>G2(x2,i2).
В итоге при решении уравнения из пункта 2, мы получим критерий Келли. Решать это уравнение лучше всего при помощи специализированных математических программ, например, MathCAD. Можно также воспользоваться Excel и инструментом «Поиск решения». Четвертый и пятый пункты служат для оценки эффективности торговой системы и позволяют оценить средний прирост капитала. Рассчитанный по данной формуле, критерий Келли будет обладать всеми достоинствами, перечисленными выше – нулевой вероятностью разорения и оптимальной скоростью прироста капитала.
Применение на практике
Скорее всего, если вы дочитали до этого места, вы все равно так и не поняли, как же рассчитать критерий Келли. Разберемся на простом примере. Итак, у нас есть трендовая система, которая сделала 100 сделок, 10 из которых дали результат +20%, еще 30 дали +40%, остальные были проигрышными – двадцать по -30% и сорок по -10%. Напомню: доход и убыток считаются, как процент от размера капитала до сделки. Система делает всего 30 сделок в год – система трендовая, скажем, на дневках, работает по одной валютной паре. Итак, мы имеем 4 различных исхода +0.2, +0.4, -0.3, -0.1, а повторялись они 10, 30, 20 и 40 раз, то есть у нас есть a1…a4 и k1…k4. Для начала давайте проверим, что математические ожидание положительно, иначе не имеет смысла применять критерий Келли. Подставим в формулу из 1 пункта: 0.2*10+0.4*30-0.3*20-0.1*40 = 2+12-6-4 = 4>0, все хорошо, система может давать прибыль. Составим уравнение из пункта 2:
E(x) = 0.2*10/(1+0.2х) + 0.4*30/(1+0.4х) — 0.3*30/(1-0.3х) — 0.1*40/(1-0.1х) = 2/(1+0.2х)+12/(1+0.4х)-6/(1-0.3х)-4/(1-0.1х) и E(x) = 0. Также у нас есть критерий – при E(f)=0 у нас есть единственный корень уравнения 0
Сегодня мы с вами разберем, что же такое критерий Келли и как его применять на рынке без сложных формул и математических терминов. Все выводы и доказательства, исследования, теоремы и прочие сложности — будут опущены, а вместо этого я расскажу о самих результатах всех страшных вышеперечисленных вещей простым и понятным языком.
История критерия Келли
Как и стратегии Д‘Аламбера с Мартингейлом, критерий Келли известен любителям ставок на спорт уже много лет. Проблему оптимальной ставки пытаются решить еще с восемнадцатого столетия, с обсуждения Даниилом Бернулли Санкт-Петербургского Парадокса. Даже в этом вопросе точки зрения разделились – одни пытаются минимизировать вероятность потерять весь депозит за определенное количество будущих сделок, другие же, наоборот, хотят за это количество сделок получить максимально возможный прирост. Еще один подход состоит в том, чтобы оценить деньги, используя функцию полезности. Иными словами, все сводится к тому, чтобы максимально полезно использовать свой депозит. Даниил Бернулли в 18 веке использовал функцию полезности при попытке решения Санкт-Петербургского Парадокса, но безуспешно.
О формуле вспомнил Джон Ларри Келли в 1956 году, заметив ее некоторые интересные свойства. В то время он работал на фирму AT&T Bell Laboratories, занимающуюся телекоммуникациями, электронными и компьютерными системами. Строго говоря, эта формула была им применена именно в этой сфере. Затем, пятью годами позже эти свойства были изучены и обобщены в исследовании Бримана. Ну а уже Марковиц в том же году решил применить формулу к ценным бумагам. А спустя еще год, в 1962 году, Эдвард О. Торп подробно описал критерий в первом издании своей книги Beat the Dealer («Побить дилера»). Такая вот нелегкая история у этого критерия, названного не в честь реального автора и получившего распространение на финансовых рынках также по воле совсем другого человека.
Что такое критерий Келли и как его рассчитать?
Критерий Келли обладает рядом свойств для заданной торговой системы с положительным математическим ожиданием и вот самые «волшебные» из них:
размер капитала неограниченно растет;
вероятность разорения игрока стремится к нулю при увеличении числа трейдов.
И действительно, при применении критерия Келли капитал будет расти быстрее, чем при применении любого другого метода управления средствами. На самом деле, определяя размер лота по этому методу, трейдер действует оптимально, но только в очень частном случае. Под самой оптимальностью тут понимается вот что:
максимально быстрое достижение капиталом заранее заданной величины;
достижение максимальной величины капитала после фиксированного числа сделок.
Пахнет разгоном, не так ли? Совершенно верно, и немного позже вы поймете, почему.
А для начала давайте разберемся с формулой критерия Келли. В литературе можно найти огромное количество различных формул для расчета, и все они будут верны. В сети встречается очень много вариантов формул для беттинга, которые также авторы статей пытаются применить к финансовым рынкам. Самая общая из встреченных мной формул выглядит так:
X = p – q/w, где:
p – вероятность выигрыша;
q – вероятность проигрыша;
w – средняя величина выигрыша (также часто рекомендуют использовать среднюю величину выигрыша относительно среднего проигрыша).
Исходя из формулы, вы всегда должны ставить в каждой сделке x от размера вашего капитала. То есть если x = 0.1, то при каждой сделке нужно ставить 10% от вашего капитала. Приведенную выше формулу далее давайте будем называть «простым» критерием Келли.
Если TAKE PROFIT = STOP LOSS, т.е. W=1, формула упрощается до: F = P(W) — P(L).
Таким образом, если вероятность выигрыша составляет 60%, то F=20%.
Давайте попробуем применить критерий Келли, высчитанный по такой формуле, к системе со стопом, тремя уровнями тейкпрофита, безубытком, двумя различными видами трейлинг стопа и выходом по стохастику:

Система имеет 78.06% прибыльных сделок со средней прибылью 9.59$ и средним убытком -25,23$.
Давайте перенесем статистику в Excel, чтобы дальше производить наши вычисления. Построим график прироста депозита фиксированным лотом 0.1:

Теперь рассчитаем для нашей системы критерий Келли по формуле X = p – q/w:
Х = 78,06 – 21,94/(9,59/25,23) = 20,32%.
Соответствующий график:

Наш депозит показал пик на отметке 1 724 000, а затем мы попали в серию неудачных сделок, что снизило наш баланс до 997 000.
Оптимальность критерия Келли
Относительная скорость роста капитала в зависимости от выбранного плеча будет пропорциональна k-0.5*k^2, где k — критерий Келли. Первое слагаемое понятно — в первом приближении скорость должна быть пропорциональна плечу, так вроде бы и следует из здравого смысла. Второе слагаемое описывает убыток пересчета, который при небольших плечах практически незаметен, но быстро увеличивается с ростом плеча и после Келли жестко убивает доходность в ноль — территория больших критериев заканчивается «ямой для особо жадных».

С увеличением плеча прибыль растет линейно, а убыток пересчета, как видно из формулы, нарастает квадратично. Это приводит к тому, что с увеличением плеча общая доходность торговли растет все меньше и меньше, а после достижения некоторого оптимума начинает падать и вскоре уходит в минус. Получается странная вещь – имеем, к примеру, довольно неплохую стратегию с множеством прибыльных сделок, принимаем решение поднять плечо до максимума с целью выжать побольше дохода, и в результате неожиданно получаем полную потерю счета.
Скорость роста достигает оптимума при значении плеча Nk, соответствующему критерию Келли, и с дальнейшим повышением плеча начинает снижаться, быстро достигая нуля и уходя в отрицательную зону для избыточно больших плеч («яма для жадных»). Теперь должно быть понятно, что есть оптимальное плечо, на котором мы имеем максимальную доходность, и выше которого убыток пересчета начитает убивать прибыль. С увеличением плеча выше оптимального, несмотря на растущую волатильность счета, итоговая прибыль становится все меньше и меньше.
Выходит, нельзя повышать плечо, не зная заранее его оптимальный по Келли уровень для используемой стратегии. Результаты могут неприятно удивить. Выше критерия Келли следует обрыв доходности вниз, можно влететь в него и попасть в «яму для жадных». Именно поэтому не стоит использовать полученный критерий без искусственного уменьшения.
Ограничения стандартной формулы
Почти нигде не написано, что в такой формулировке критерий Келли предполагает, что в торговой системе могут быть только результаты:
-1хСтавка (то есть трейдер проигрывает при х=0.1 ровно 10% от депозита);
+ wхСтавка (то есть или выигрыш w, или проигрыш -1).
Такой вариант, как вы видите, довольно частный случай, в котором исхода у сделки может быть только два – либо стоп лосс, либо тейк профит. А вот более обобщенный вариант, где возможно большое число различных результатов каждой сделки (например, в системах с применением безубытка, трейлинг стопа и выхода по системе), такой вариант расчета не подойдет.
Поэтому необходимо обобщить формулу расчета критерия Келли. Опуская теоретические выкладки, доказательства и формулировки, я приведу лишь конечный результат.
Обобщенная формула критерия Келли
Пусть у нас есть торговая система, которая дала следующие результаты {ai,ki} при i=0…n, где k – количество сделок с одним результатом, a – их результат, i – количество сделок. Чтобы было понятнее: мы совершили по системе кучу сделок и разбили эти сделки по результатам. Получилось у нас, например, 10 сделок по бу (0%), 30 сделок с профитом 2%, 20 сделок с убытком -3% и так далее. Таких вариантов у нас может быть сколько угодно много, их i штук. В каждом таком наборе у нас количество сделок с одним результатом (k) и сам результат (a). Если a>0, то сделка или сделки закрылись с прибылью, если a<0, то с убытком.
Сделки с нулевым результатом можно отбросить, на конечный результат системы они не влияют. Теперь будем считать, что все сделки (или кучки сделок с одинаковыми результатами) у нас упорядочены по возрастанию, при этом у нас есть хотя бы одна кучка убыточных сделок, то есть a1 0. А случается такое, когда математические ожидание системы положительно. Если сумма всех aiki меньше либо равно нулю, система обречена на слив и никакая система управления капиталом тут не поможет.
Введем функцию:
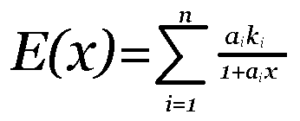
Известно, что существует и единственно 01, то, ставя x, трейдер пришел к успеху.
И последний пункт, касающийся скорее сравнения двух систем. Пусть у нас есть две системы {a1i,k1i} и {a2i,k2i} с положительным математическим ожиданием, которые были испытаны на одинаковом интервале времени. Первая система сделала i1 сделок, вторая i2 сделок, трейдер ставил в первой системе х1, во второй х2. Тогда первая система будет эффективней второй, если G1(x1,i1)>G2(x2,i2).
В итоге при решении уравнения из пункта 2, мы получим критерий Келли. Решать это уравнение лучше всего при помощи специализированных математических программ, например, MathCAD. Можно также воспользоваться Excel и инструментом «Поиск решения». Четвертый и пятый пункты служат для оценки эффективности торговой системы и позволяют оценить средний прирост капитала. Рассчитанный по данной формуле, критерий Келли будет обладать всеми достоинствами, перечисленными выше – нулевой вероятностью разорения и оптимальной скоростью прироста капитала.
Применение на практике
Скорее всего, если вы дочитали до этого места, вы все равно так и не поняли, как же рассчитать критерий Келли. Разберемся на простом примере. Итак, у нас есть трендовая система, которая сделала 100 сделок, 10 из которых дали результат +20%, еще 30 дали +40%, остальные были проигрышными – двадцать по -30% и сорок по -10%. Напомню: доход и убыток считаются, как процент от размера капитала до сделки. Система делает всего 30 сделок в год – система трендовая, скажем, на дневках, работает по одной валютной паре. Итак, мы имеем 4 различных исхода +0.2, +0.4, -0.3, -0.1, а повторялись они 10, 30, 20 и 40 раз, то есть у нас есть a1…a4 и k1…k4. Для начала давайте проверим, что математические ожидание положительно, иначе не имеет смысла применять критерий Келли. Подставим в формулу из 1 пункта: 0.2*10+0.4*30-0.3*20-0.1*40 = 2+12-6-4 = 4>0, все хорошо, система может давать прибыль. Составим уравнение из пункта 2:
E(x) = 0.2*10/(1+0.2х) + 0.4*30/(1+0.4х) — 0.3*30/(1-0.3х) — 0.1*40/(1-0.1х) = 2/(1+0.2х)+12/(1+0.4х)-6/(1-0.3х)-4/(1-0.1х) и E(x) = 0. Также у нас есть критерий – при E(f)=0 у нас есть единственный корень уравнения 0
Не является индивидуальной инвестиционной рекомендацией | При копировании ссылка обязательна | Нашли ошибку - выделить и нажать Ctrl+Enter | Жалоба

