1 сентября 2022 Доходъ
В случаях, когда вы знаете риск и ожидаемую доходность различных инвестиционных портфелей, и все они вас устраивают, оценка уровня диверсификации может быть дополнительным инструментом выбора подходящей структуры инвестиций или ее улучшения. В этой статье мы расскажем о методах измерения такого уровня.
Когда нужно измерять уровень диверсификации
Прежде всего, необходимо отметить, что диверсификация, хотя и является эффективным способом снижения несистематического (нерыночного) риска инвестиций, не является панацеей от всех проблем, возникающих при инвестировании, а излишний ее уровень может быть вреден для затрат (и, в конечном счете, доходности) портфеля, а также для инвестиционных целей/стратегий инвесторов.
Базовый уровень диверсификации (скажем, наличие от 10 до 20 различных бумаг в портфеле акций) необходим, потому что все мы можем ошибаться, когда принимаем решения об активных инвестициях (выбираем акции или классы активов) и, тем более, когда не принимаем таких решений (например, инвестируя в базовые портфели фондов акций и облигаций в удобной для себя пропорции).
Но метрики, описываемые в этой статье, скорее, являются лишь дополнительными инструментами для принятия решений - например, когда вам необходимо сравнить похожие портфели или понять нуждается портфель в улучшении.
Данные для иллюстрации уровней диверсификации
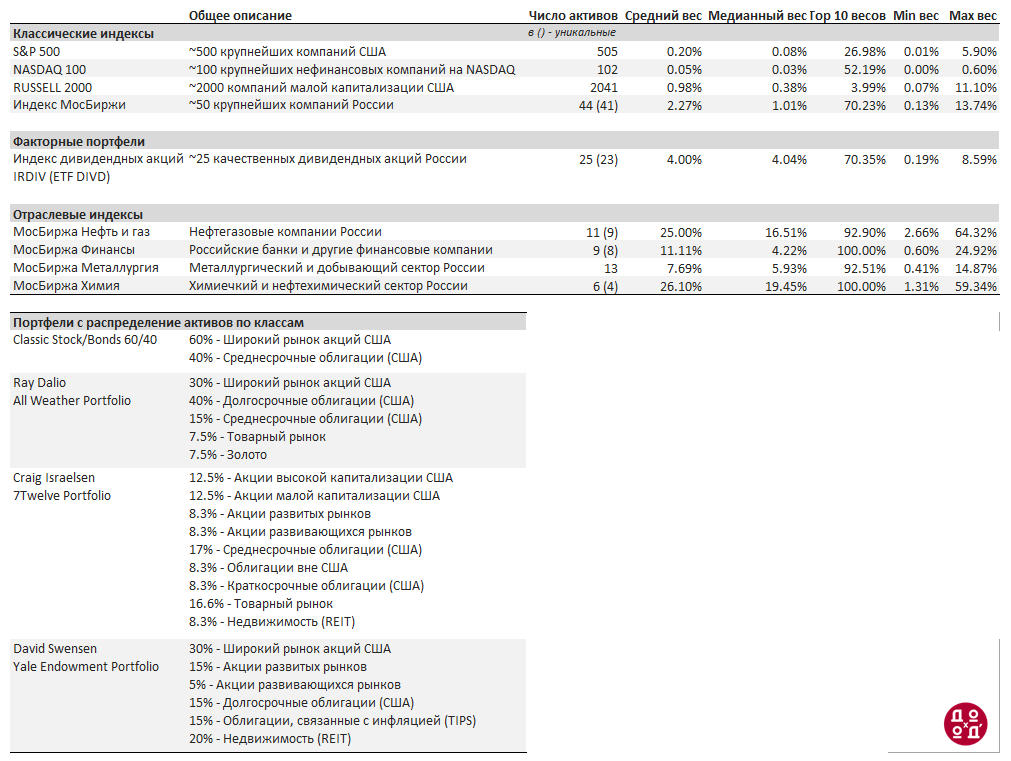
Для иллюстрации различных уровней диверсификации, мы провели расчет показателей, описанных ниже, для 10 индексных портфелей акций и 4-х портфелей, инвестирующих в разные классы активов (через ETF). Таблицы ниже дают их общее описание. В конце статьи вы найдете таблицу с итогами расчетов.
Показатели диверсификации
Ниже мы рассмотрим следующие показатели оценки уровня диверсификации:
Индекс Херфиндаля-Хиршмана;
Энтропия Шенона;
Энтропия Ягера;
Коэффициент концентрации;
Внутрипортфельная корреляция и ее производные.
1. Индекс Херфиндаля-Хиршмана (Herfindail index)
Данный индекс изначально был разработан Альбертом Отто Хиршманом для оценки монополизации рынка, и представлял из себя корень из суммы квадратов долей всех участников рынка.
Пять лет спустя он был повторно разработан Оррисом К. Херфиндалем, который не знал о работе своего предшественника, но с небольшим изменением: теперь он стал считаться как сумма квадратов долей всех участников рынка, без корня.
Позже этот показатель стал использоваться для оценки диверсификации портфеля акций - веса акций заменили доли участников рынка.
Основная задача индекса Херфиндаля – определить, не сконцентрирована ли большая доля средств в одном активе. Он расчитывается согласно следующей формуле:
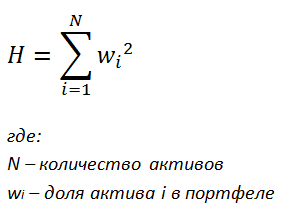
Чем меньше значение индекса, тем портфель менее концентрирован и наоборот.
Максимальная диверсификация будет достигаться при равном значении долей стремящемся к нулю.
Таким образом, для данного показателя важно, что бы в портфеле было много активов, а их доли были приближены к равным.
Для оценки монополизации рынка используются следующие пороговые значения:
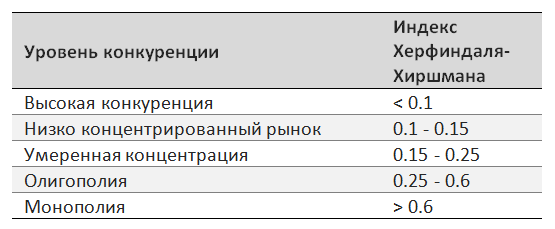
Для портфеля акций эти значения в целом справедливы. Вы можете "монополизировать" свой портфель, если уверены в перспективах выбранных акций и понимаете риски такой концентрации отельных акций.
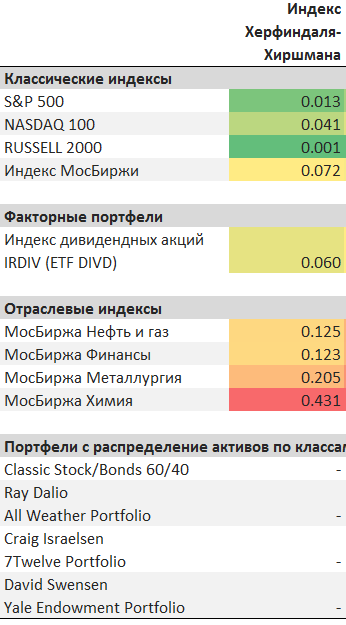
Индекс Russel 2000 ожидаемо получает наивысшее значение данного показателя за счет большого количества активов и достаточно низкой концентрации средств в одной позиции. Индекс химического сектора МосБиржи также ожидаемо хуже - с 6 акциями в составе (и 4 акциями уникальных эмитентов) и почти 60% долей в бумагах Фосагро.
Интересно, что наш индекс дивидендных акций IRDIV (на его основе собран ETF DIVD) показывает более высокое значение индекса, чем индекс МосБиржи. Так получается за счет более равных весов (собственно меньшей концентрации активов) в IRDIV.
Ограничения
Индекс Херфиндаля-Хиршмана имеет смысл применять только для портфелей с одним типов активов. Различная природа взаимосвязи доходностей, например, акций и облигаций, снижают эффективность оценки диверсификации только на основе весов активов.
При прочих равных, этот индекс не отличает концентрацию на одного эмитента. Поэтому входные данные необходимо корректировать соответствующим образом и/или устанавливать отдельное ограничение веса на одного эмитента.
2. Энтропия Шенона (Shanon entropy)
Данный показатель был разработан Клодом Элвудом Шеноном, американским инженером и криптоаналитиком и математиком. Именно он придумал использовать слово «бит», в том понимании, в котором мы его понимаем сегодня.
Энтропия – это мера неопределенности в какой-либо системе, она характеризует конкретность информации.
Если вы высоко оцениваете перспективы какой-то акции и активно управление портфелем, то, вероятно, ее доля в вашем портфеле будет относительно высокой. Ваша уверенность в этом активе, в теории, снижает неопределенность, а вслед за ней снижается энтропия.
Допустим у нас есть два портфеля: один состоит из двух активов с равными долями по 50%, а другой из 20 активов по 5%.
В первом случае считается, что вы уверены в результативности двух активов, и поэтому вложились только в них.
Во втором случае, вы недостаточно уверены в своем выборе или просто знаете, что ошибок и случайностей не избежать, поэтому, предпочли разбить свой портфель на 20 частей.
Таким образом, идеальное значение с точки зрения энтропии равное нулю, вы получите, если купите только один единственный актив, в котором будете на 100% уверенны. Неопределенность будет минимальной, но это, конечно, недостижимо в реальном мире.
Другая крайность - максимизация энтропии (неопределенности), что будет означать идеальную диверсификацию - "недоверие" к множеству активов в портфеле с маленькими равными весами.
Энтропия Шенона рассчитывается согласно следующей формуле:

Чем больше значение, тем больше уровень диверсификации.
Максимальный результат будет достигаться при равном значении весов стремящимся к нулю.
В данной модели, в сравнении с индексом Херфиндаля, отдается предпочтение портфелям с большим количеством активов. В соответствии с этим и расположились оценки для исследуемых портфелей.
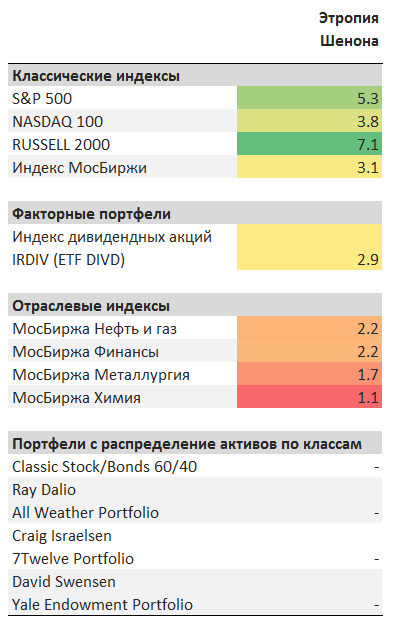
Ограничения
Энтропия Шенона имеет ограничения для применения аналогичные индексу Херфиндаля-Хиршмана.
3. Энтропия Ягера (Yager entropy)
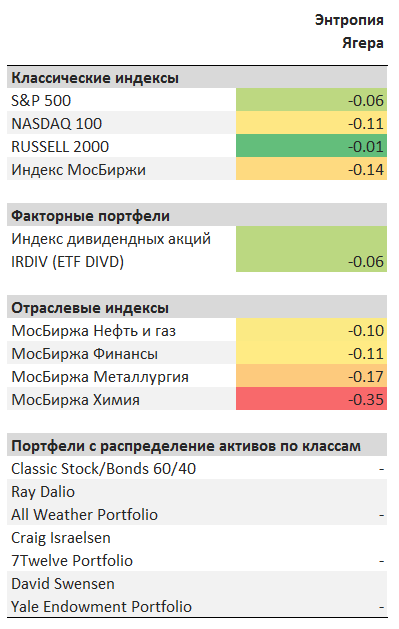
Энтропия Ягера позволяет выявить, насколько веса активов в портфеле отличаются друг от друга. Другими словами - это универсальный инструмент для поиска наиболее равновзвешенных портфелей.

Максимальное значение – ноль, достигается при условии, что все доли равны.
Чем больше различие между весами долей, тем меньше (меньше нуля) значение энтропии Ягера и портфель считается менее диверсифицированным.
Ограничения
Энтропия Ягера имеет ограничения для применения аналогичные индексу Херфиндаля-Хиршмана.
4. Коэффициент концентрации (Concentration coefficient)
Коэффициент концентрации выполняет схожую функцию с энтропией Ягера – выявление портфелей с неравномерным распределением средств, что может привести к высокой концентрации вложений.
Однако, в данной модели учитывается также количество активов в портфеле. К примеру, если в энтропии Ягера портфель с двумя долями по 50% будет считаться лучше портфеля с распределением 1 актив - 2%, и 98 активов по 1%, то тут будет наоборот.
Формула для расчета коэффициента концентрации следующая:
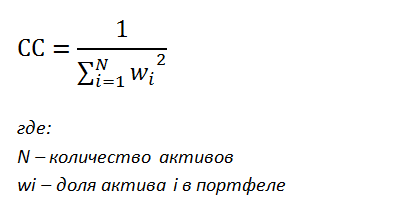
Минимальная концентрация достигается при значении коэффициента равного бесконечности - при бесконечном количестве долей стремящимся к нулю, которые будут равны между собой.
Максимальная концентрация достигается при значении равным единице - при вложении всех средств в один единственный актив.
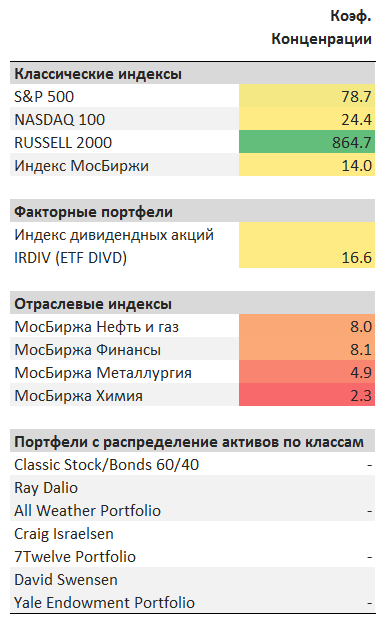
Ограничения
Коэффициент концентрации имеет ограничения для применения аналогичные индексу Херфиндаля-Хиршмана.
5. Внутрипортфельная корреляция (Intra-portfolio correlation - IPC)
Внутрипортфельная корреляция приносит кое-что новое в наши расчеты, а именно позволяет использовать для оценки уровня диверсификации не только веса активов в портфеле, но и корреляцию (взаимосвязь) между ними. Это, в частности, позволяет оценить более сложны портфели, состоящие из различных классов активов (акции, облигации, товары и пр.).
Этот показатель измеряет средневзвешенное значение для всех уникальных корреляций активов в портфеле. Формула для расчета следующая:
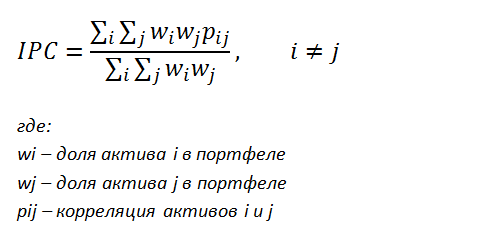
Чем ниже внутрипортфельная корреляция, тем более диверсифицированным является портфель.
Полученный результат варьируется от -1 до 1, где -1 означает, что вы снизили диверсифицируемый (несистематический, нерыночный) риск на 100%, а 1 - что такой риск не снижен совсем.
Отрицательные значения IPC, как правило, говорят о применении коротких позиций или других методик хеджирования.
Следующая таблица связывает показатель IPC с уровнем снижения несистематического риска (IPC%).
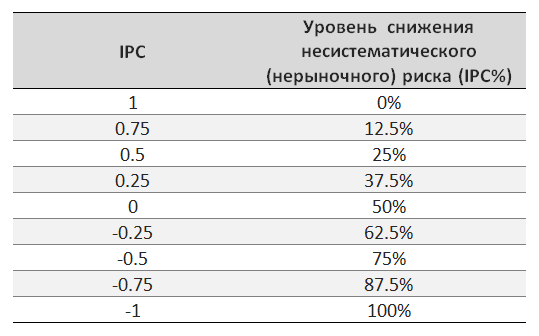
Для облегчения перевода показателя IPC в IPC% можно использовать следующую формулу:
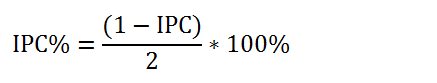
Таблица ниже отражает результаты расчётов IPC и IPC%. Для сравнения приведен также показатель средней корреляции внутри портфеля (если бы он был равновзвешанным).
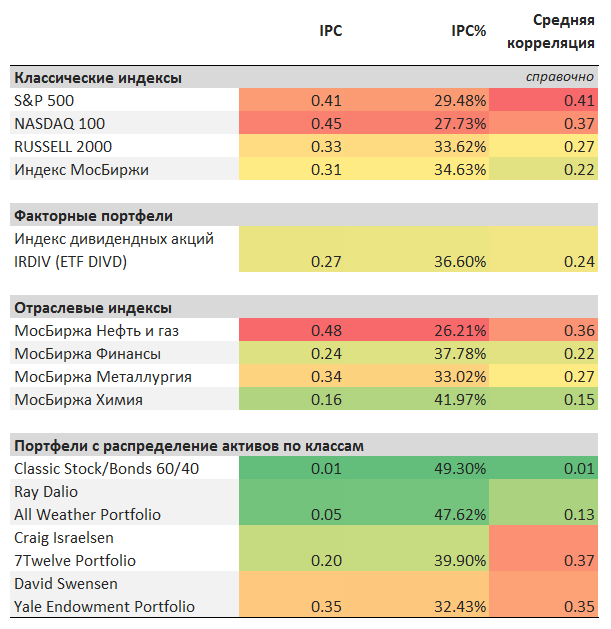
IPC3 - уточнение IPC%
IPC3 – это коэффициент диверсификации, который учитывает в себе сразу несколько показателей - коэффициент концентрации (CC) и уровень снижения диверсифицируемого риска (IPC%). Формула для его расчета следующая:
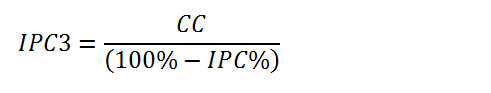
Чем больше значение показателя IPC3, тем более диверсифицированным является портфель.
Это означает, что у в портфеле есть большое число активов без ярко выраженной концентрации в одном из них, с учетом того, что активы имеют низкий уровень корреляции между собой.
К сожалению, вследствие использования коэффициента концентрации IPC3 нельзя применить для сложных портфелей, содержащих несколько классов активов.
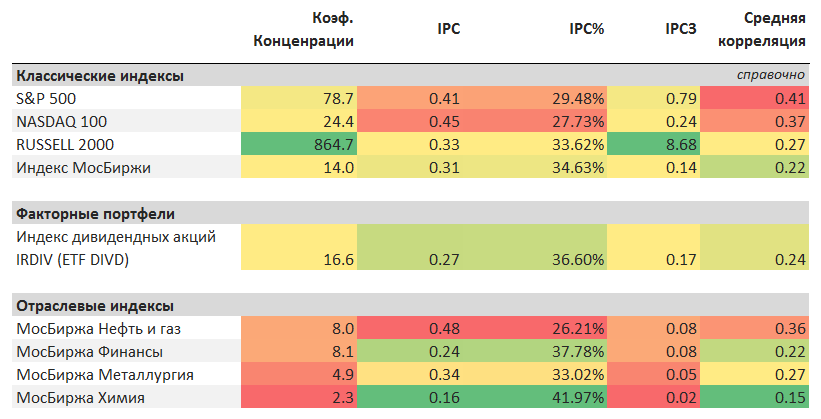
Как можно увидеть в таблице ниже такое уточнение IPC% может быть очень полезным.
Подробнее о показателях IPC можно почитать здесь и здесь (оба документа на английском).
Итоги расчетов
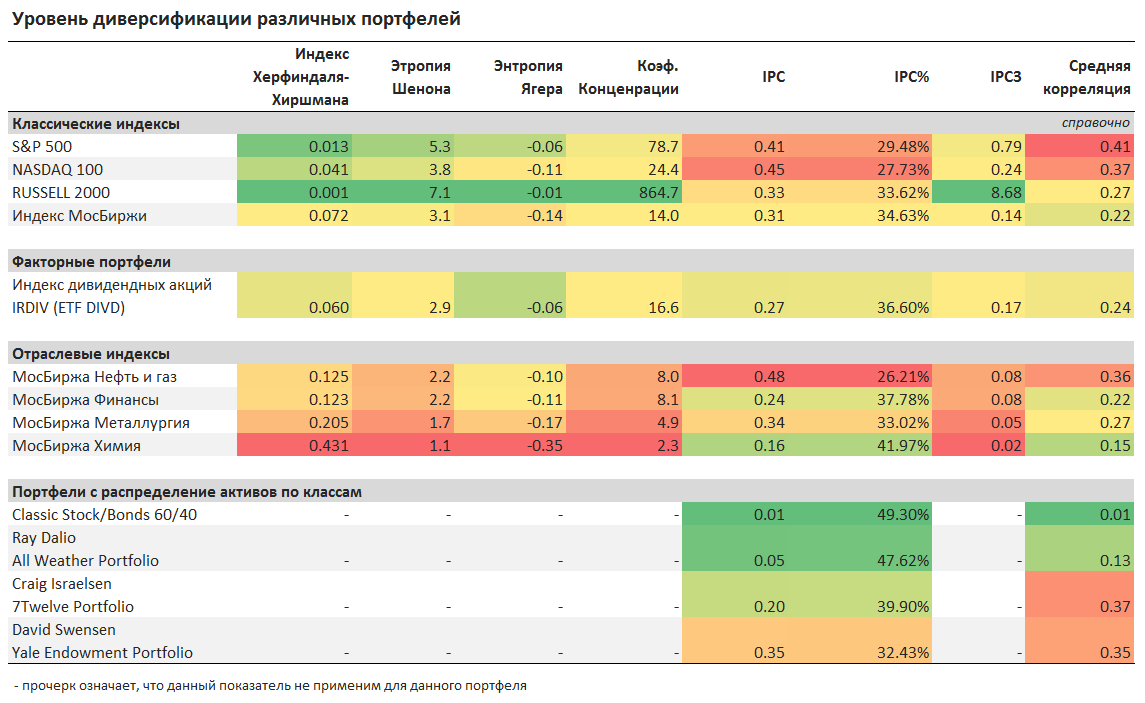
В таблице ниже приведены результаты расчета показателей уровня диверсификации для всех анализируемых портфелей.
В завершении еще раз повторим, что уровень диверсификации тесно связан с инвестиционным профилем инвестора и не нужно стремится к максимуму диверсификации во всех случаях. Общее правило - больше уверенности в портфеле и больше понимания его риска позволяет формировать менее диверсифицированные портфели и наоборот.
Когда нужно измерять уровень диверсификации
Прежде всего, необходимо отметить, что диверсификация, хотя и является эффективным способом снижения несистематического (нерыночного) риска инвестиций, не является панацеей от всех проблем, возникающих при инвестировании, а излишний ее уровень может быть вреден для затрат (и, в конечном счете, доходности) портфеля, а также для инвестиционных целей/стратегий инвесторов.
Базовый уровень диверсификации (скажем, наличие от 10 до 20 различных бумаг в портфеле акций) необходим, потому что все мы можем ошибаться, когда принимаем решения об активных инвестициях (выбираем акции или классы активов) и, тем более, когда не принимаем таких решений (например, инвестируя в базовые портфели фондов акций и облигаций в удобной для себя пропорции).
Но метрики, описываемые в этой статье, скорее, являются лишь дополнительными инструментами для принятия решений - например, когда вам необходимо сравнить похожие портфели или понять нуждается портфель в улучшении.
В контексте практического применения расчета уровня диверсификации также нужно сказать, что при базовом подходе он определяется "автоматически" (само собой) при оптимизации портфеля (математическими методами).
Однако оптимизация обычно проводится на ограниченном наборе инструментов и сравнение диверсификации оптимальных портфелей, собранных из различных таких наборов бывает особенно полезной (в частности, при формировании больших глобальных портфелей).
Показатели диверсификации также могут использоваться непосредственно в качестве ограничений (минимальных требований к концентрации портфеля) в процессе оптимизации.
Однако оптимизация обычно проводится на ограниченном наборе инструментов и сравнение диверсификации оптимальных портфелей, собранных из различных таких наборов бывает особенно полезной (в частности, при формировании больших глобальных портфелей).
Показатели диверсификации также могут использоваться непосредственно в качестве ограничений (минимальных требований к концентрации портфеля) в процессе оптимизации.
Данные для иллюстрации уровней диверсификации
Для иллюстрации различных уровней диверсификации, мы провели расчет показателей, описанных ниже, для 10 индексных портфелей акций и 4-х портфелей, инвестирующих в разные классы активов (через ETF). Таблицы ниже дают их общее описание. В конце статьи вы найдете таблицу с итогами расчетов.
Показатели диверсификации
Ниже мы рассмотрим следующие показатели оценки уровня диверсификации:
Индекс Херфиндаля-Хиршмана;
Энтропия Шенона;
Энтропия Ягера;
Коэффициент концентрации;
Внутрипортфельная корреляция и ее производные.
1. Индекс Херфиндаля-Хиршмана (Herfindail index)
Данный индекс изначально был разработан Альбертом Отто Хиршманом для оценки монополизации рынка, и представлял из себя корень из суммы квадратов долей всех участников рынка.
Пять лет спустя он был повторно разработан Оррисом К. Херфиндалем, который не знал о работе своего предшественника, но с небольшим изменением: теперь он стал считаться как сумма квадратов долей всех участников рынка, без корня.
Позже этот показатель стал использоваться для оценки диверсификации портфеля акций - веса акций заменили доли участников рынка.
Основная задача индекса Херфиндаля – определить, не сконцентрирована ли большая доля средств в одном активе. Он расчитывается согласно следующей формуле:
Чем меньше значение индекса, тем портфель менее концентрирован и наоборот.
Максимальная диверсификация будет достигаться при равном значении долей стремящемся к нулю.
Таким образом, для данного показателя важно, что бы в портфеле было много активов, а их доли были приближены к равным.
Для оценки монополизации рынка используются следующие пороговые значения:
Для портфеля акций эти значения в целом справедливы. Вы можете "монополизировать" свой портфель, если уверены в перспективах выбранных акций и понимаете риски такой концентрации отельных акций.
Индекс Russel 2000 ожидаемо получает наивысшее значение данного показателя за счет большого количества активов и достаточно низкой концентрации средств в одной позиции. Индекс химического сектора МосБиржи также ожидаемо хуже - с 6 акциями в составе (и 4 акциями уникальных эмитентов) и почти 60% долей в бумагах Фосагро.
Интересно, что наш индекс дивидендных акций IRDIV (на его основе собран ETF DIVD) показывает более высокое значение индекса, чем индекс МосБиржи. Так получается за счет более равных весов (собственно меньшей концентрации активов) в IRDIV.
Ограничения
Индекс Херфиндаля-Хиршмана имеет смысл применять только для портфелей с одним типов активов. Различная природа взаимосвязи доходностей, например, акций и облигаций, снижают эффективность оценки диверсификации только на основе весов активов.
При прочих равных, этот индекс не отличает концентрацию на одного эмитента. Поэтому входные данные необходимо корректировать соответствующим образом и/или устанавливать отдельное ограничение веса на одного эмитента.
2. Энтропия Шенона (Shanon entropy)
Данный показатель был разработан Клодом Элвудом Шеноном, американским инженером и криптоаналитиком и математиком. Именно он придумал использовать слово «бит», в том понимании, в котором мы его понимаем сегодня.
Энтропия – это мера неопределенности в какой-либо системе, она характеризует конкретность информации.
Если вы высоко оцениваете перспективы какой-то акции и активно управление портфелем, то, вероятно, ее доля в вашем портфеле будет относительно высокой. Ваша уверенность в этом активе, в теории, снижает неопределенность, а вслед за ней снижается энтропия.
Допустим у нас есть два портфеля: один состоит из двух активов с равными долями по 50%, а другой из 20 активов по 5%.
В первом случае считается, что вы уверены в результативности двух активов, и поэтому вложились только в них.
Во втором случае, вы недостаточно уверены в своем выборе или просто знаете, что ошибок и случайностей не избежать, поэтому, предпочли разбить свой портфель на 20 частей.
Таким образом, идеальное значение с точки зрения энтропии равное нулю, вы получите, если купите только один единственный актив, в котором будете на 100% уверенны. Неопределенность будет минимальной, но это, конечно, недостижимо в реальном мире.
Другая крайность - максимизация энтропии (неопределенности), что будет означать идеальную диверсификацию - "недоверие" к множеству активов в портфеле с маленькими равными весами.
Энтропия Шенона рассчитывается согласно следующей формуле:
Чем больше значение, тем больше уровень диверсификации.
Максимальный результат будет достигаться при равном значении весов стремящимся к нулю.
В данной модели, в сравнении с индексом Херфиндаля, отдается предпочтение портфелям с большим количеством активов. В соответствии с этим и расположились оценки для исследуемых портфелей.
Ограничения
Энтропия Шенона имеет ограничения для применения аналогичные индексу Херфиндаля-Хиршмана.
3. Энтропия Ягера (Yager entropy)
Энтропия Ягера позволяет выявить, насколько веса активов в портфеле отличаются друг от друга. Другими словами - это универсальный инструмент для поиска наиболее равновзвешенных портфелей.
Максимальное значение – ноль, достигается при условии, что все доли равны.
Чем больше различие между весами долей, тем меньше (меньше нуля) значение энтропии Ягера и портфель считается менее диверсифицированным.
Ограничения
Энтропия Ягера имеет ограничения для применения аналогичные индексу Херфиндаля-Хиршмана.
4. Коэффициент концентрации (Concentration coefficient)
Коэффициент концентрации выполняет схожую функцию с энтропией Ягера – выявление портфелей с неравномерным распределением средств, что может привести к высокой концентрации вложений.
Однако, в данной модели учитывается также количество активов в портфеле. К примеру, если в энтропии Ягера портфель с двумя долями по 50% будет считаться лучше портфеля с распределением 1 актив - 2%, и 98 активов по 1%, то тут будет наоборот.
Формула для расчета коэффициента концентрации следующая:
Минимальная концентрация достигается при значении коэффициента равного бесконечности - при бесконечном количестве долей стремящимся к нулю, которые будут равны между собой.
Максимальная концентрация достигается при значении равным единице - при вложении всех средств в один единственный актив.
Ограничения
Коэффициент концентрации имеет ограничения для применения аналогичные индексу Херфиндаля-Хиршмана.
5. Внутрипортфельная корреляция (Intra-portfolio correlation - IPC)
Внутрипортфельная корреляция приносит кое-что новое в наши расчеты, а именно позволяет использовать для оценки уровня диверсификации не только веса активов в портфеле, но и корреляцию (взаимосвязь) между ними. Это, в частности, позволяет оценить более сложны портфели, состоящие из различных классов активов (акции, облигации, товары и пр.).
Этот показатель измеряет средневзвешенное значение для всех уникальных корреляций активов в портфеле. Формула для расчета следующая:
Чем ниже внутрипортфельная корреляция, тем более диверсифицированным является портфель.
Полученный результат варьируется от -1 до 1, где -1 означает, что вы снизили диверсифицируемый (несистематический, нерыночный) риск на 100%, а 1 - что такой риск не снижен совсем.
Отрицательные значения IPC, как правило, говорят о применении коротких позиций или других методик хеджирования.
Следующая таблица связывает показатель IPC с уровнем снижения несистематического риска (IPC%).
Для облегчения перевода показателя IPC в IPC% можно использовать следующую формулу:
Таблица ниже отражает результаты расчётов IPC и IPC%. Для сравнения приведен также показатель средней корреляции внутри портфеля (если бы он был равновзвешанным).
IPC3 - уточнение IPC%
IPC3 – это коэффициент диверсификации, который учитывает в себе сразу несколько показателей - коэффициент концентрации (CC) и уровень снижения диверсифицируемого риска (IPC%). Формула для его расчета следующая:
Чем больше значение показателя IPC3, тем более диверсифицированным является портфель.
Это означает, что у в портфеле есть большое число активов без ярко выраженной концентрации в одном из них, с учетом того, что активы имеют низкий уровень корреляции между собой.
К сожалению, вследствие использования коэффициента концентрации IPC3 нельзя применить для сложных портфелей, содержащих несколько классов активов.
Как можно увидеть в таблице ниже такое уточнение IPC% может быть очень полезным.
Индекс химического сектора МосБиржи имеет очень хороший показатель IPC% вследствие относительно низкой корреляции (см. среднюю корреляцию) внутри портфеля, но при этом он является высококонцентрированным, поэтому коэффициент IPC3 более адекватно оценивает его общую диверсификацию.
Подробнее о показателях IPC можно почитать здесь и здесь (оба документа на английском).
Итоги расчетов
В таблице ниже приведены результаты расчета показателей уровня диверсификации для всех анализируемых портфелей.
Особое внимание стоит обратить на показатель внутрепортфельной корреляции (IPC) и его производные (IPC%) для портфелей с разнообразными классами активов. Более высокий уровень диверсфикации здесь отлично показывает преимущества глобальных диверсифицированных портфелей.
В завершении еще раз повторим, что уровень диверсификации тесно связан с инвестиционным профилем инвестора и не нужно стремится к максимуму диверсификации во всех случаях. Общее правило - больше уверенности в портфеле и больше понимания его риска позволяет формировать менее диверсифицированные портфели и наоборот.
Не является индивидуальной инвестиционной рекомендацией | При копировании ссылка обязательна | Нашли ошибку - выделить и нажать Ctrl+Enter | Жалоба

