Задачи на расчёт оптимизации производства товаров и услуг
Задачи на расчёт оптимизации производства товаров и услуг были включены во вторую часть ЕГЭ по математике профильного уровня недавно.
Эти задачи связаны со знанием некоторых специфических математических моделей из области экономики, с умением переводить сформулированные в виде текста условия в уравнения и неравенства и пониманием того, как решения полученных уравнений и неравенств соотносятся с условием задачи. Кроме владения математическим инструментарием, для успешного решения подобных задач требуется умение строить простейшие математические модели по заданным условиям.
Разберём экономические задачи, в которых можно обойтись без исследования целевой функции, решив их с помощью логического перебора.
Задачи для разбора взяты из реальных вариантов ЕГЭ прошлых лет, которые размещены на популярном среди школьников и учителей сайте РЕШУ ЕГЭ.
Задача 1. Рассчитать наибольший доход, который можно получить
У фермера есть два поля, каждое площадью 10 га. На каждом из них можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 300 ц/га, а на втором — 200 ц/га. Урожайность свёклы на первом поле равна 200 ц/га, на втором — 300 ц/га.
Фермер может продавать картофель по цене 10 000 руб./ц, а свёклу — по цене 13 000 руб./ц. Какой наибольший доход может получить фермер?
Решение
Свёкла стоит дороже, следовательно, продавать её более выгодно. Учитывая то, что на втором поле урожайность свёклы выше, его следует засадить только этой культурой.
Доход от продажи свёклы со второго поля составит:
10 га * 300 ц/га * 13 000 руб./ц = 39 000 000 руб.
Урожайность свёклы на первом поле равна 200 ц/га.
Если всё первое поле засеять свёклой, то доход составит:
10 га * 200 ц/га * 13 000 руб./ц = 26 000 000 руб.
Если всё первое поле засеять картофелем, то доход составит:
10 га * 300 ц/га * 10 000 = 30 000 000 руб.
С единицы площади первого поля доход от картофеля будет больше, чем доход от свёклы. Следовательно, всё первое поле следует засеять картофелем.
Таким образом, наибольший возможный доход фермера равен:
39 млн + 30 млн = 69 млн руб.
Ответ: 69 млн руб.
Задача 2. Рассчитать объём продукции, который может быть произведён
В двух шахтах добывают алюминий и никель. В первой шахте имеется 20 рабочих, каждый из которых готов трудиться пять часов в день. При этом один рабочий за час добывает 1 кг алюминия или 2 кг никеля. Во второй шахте имеется 100 рабочих, каждый из которых готов трудиться пять часов в день. При этом один рабочий добывает за час 2 кг алюминия или 1 кг никеля.
Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом шахты договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?
Решение
Пусть в первой шахте х рабочих, а во второй — у рабочих заняты на добыче алюминия (х и у — целые; x 0; y 0).

По условию на 2 кг алюминия приходится 1 кг никеля, то есть алюминия необходимо добывать вдвое больше.
Значит, 5х + 10у = 2 * (700 – 10х – 5у), откуда 5х + 4у = 280 (1), следовательно: 5х = 280 – 4y.
Из равенства (1) следует, что наибольшее возможное значение у равно 70 (при х = 0).
Пусть s — масса сплава (две части алюминия и одна часть никеля), которая втрое больше массы добытого никеля, следовательно:
s = 3 * (700 – 10х – 5у) = 3 * (700 – 2(280 – 4у) – 5у) = 3 * (700 – 560 + 8у – 5у) = 3 * (140 + 3у).
Так как наибольшее возможное значение у равно 70, то наибольшее значение массы сплава составляет:
s = 3 * (140 + 3 * 70) = 1050 кг
Таким образом, 70 рабочих второй шахты должны быть заняты на добыче алюминия, остальные 30 рабочих второй шахты и все 20 рабочих первой шахты — на добыче никеля.
При этом будет добыто 700 кг алюминия и 350 кг никеля, а масса сплава составит 1050 кг.
Ответ: 1050 кг.
В следующей задаче главная сложность для получения её математической модели — понять, какая величина выбирается в качестве неизвестной.
Задача 3. Рассчитать максимально возможную прибыль
Фабрика, которая производит пищевые полуфабрикаты, выпускает блинчики со следующими видами начинки: ягодная и творожная. В таблице приведены себестоимость и отпускная цена, а также производственные возможности фабрики по каждому виду продукта при полной загрузке всех мощностей только данным видом.

Для выполнения условий ассортиментности, которые предъявляются торговыми сетями, продукции каждого вида должно быть выпущено не менее 15 т. Предполагая, что вся продукция фабрики находит спрос (реализуется без остатка), найдите максимально возможную прибыль, которую может получить фабрика от производства блинчиков за один месяц.
Решение
Пусть x — доля мощностей завода, занятых под производство блинчиков с ягодной начинкой, а y — доля мощностей, занятых под производство блинчиков с творожной начинкой, следовательно: x + y = 1.
90x т — производится блинчиков с ягодной начинкой.
75y т — производится блинчиков с творожной начинкой.
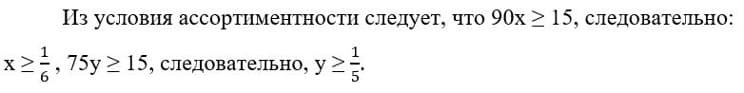
Прибыль с 1 т блинчиков с ягодной начинкой: 100 – 70 = 30 тыс. руб.
Прибыль с 1 т блинчиков с творожной начинкой: 135 – 100 = 35 тыс. руб.
Общая прибыль с произведённой за месяц продукции составит:
S (x, y) = 30 * 90х + 35 * 75y = 2700х + 2625у = 75 * (36x + 35y)
Следует найти наибольшее значение функции S (x, y) = 75 * (36x + 35y) при выполнении следующих условий:
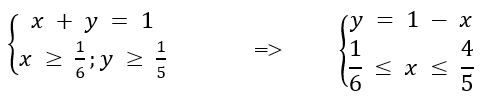
Подставляя у = 1 − x в выражение 36x + 35y, получаем:
36x + 35 * (1 − x) = x + 35
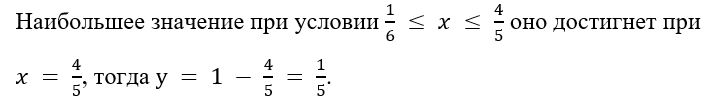
Максимально возможная прибыль завода за месяц составит:
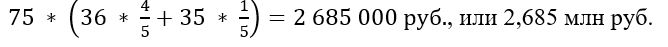
Ответ: 2,685 млн руб.
Задачи на расчёт оптимизации производства товаров и услуг были включены во вторую часть ЕГЭ по математике профильного уровня недавно.
Эти задачи связаны со знанием некоторых специфических математических моделей из области экономики, с умением переводить сформулированные в виде текста условия в уравнения и неравенства и пониманием того, как решения полученных уравнений и неравенств соотносятся с условием задачи. Кроме владения математическим инструментарием, для успешного решения подобных задач требуется умение строить простейшие математические модели по заданным условиям.
Разберём экономические задачи, в которых можно обойтись без исследования целевой функции, решив их с помощью логического перебора.
Задачи для разбора взяты из реальных вариантов ЕГЭ прошлых лет, которые размещены на популярном среди школьников и учителей сайте РЕШУ ЕГЭ.
Задача 1. Рассчитать наибольший доход, который можно получить
У фермера есть два поля, каждое площадью 10 га. На каждом из них можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 300 ц/га, а на втором — 200 ц/га. Урожайность свёклы на первом поле равна 200 ц/га, на втором — 300 ц/га.
Фермер может продавать картофель по цене 10 000 руб./ц, а свёклу — по цене 13 000 руб./ц. Какой наибольший доход может получить фермер?
Решение
Свёкла стоит дороже, следовательно, продавать её более выгодно. Учитывая то, что на втором поле урожайность свёклы выше, его следует засадить только этой культурой.
Доход от продажи свёклы со второго поля составит:
10 га * 300 ц/га * 13 000 руб./ц = 39 000 000 руб.
Урожайность свёклы на первом поле равна 200 ц/га.
Если всё первое поле засеять свёклой, то доход составит:
10 га * 200 ц/га * 13 000 руб./ц = 26 000 000 руб.
Если всё первое поле засеять картофелем, то доход составит:
10 га * 300 ц/га * 10 000 = 30 000 000 руб.
С единицы площади первого поля доход от картофеля будет больше, чем доход от свёклы. Следовательно, всё первое поле следует засеять картофелем.
Таким образом, наибольший возможный доход фермера равен:
39 млн + 30 млн = 69 млн руб.
Ответ: 69 млн руб.
Задача 2. Рассчитать объём продукции, который может быть произведён
В двух шахтах добывают алюминий и никель. В первой шахте имеется 20 рабочих, каждый из которых готов трудиться пять часов в день. При этом один рабочий за час добывает 1 кг алюминия или 2 кг никеля. Во второй шахте имеется 100 рабочих, каждый из которых готов трудиться пять часов в день. При этом один рабочий добывает за час 2 кг алюминия или 1 кг никеля.
Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом шахты договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?
Решение
Пусть в первой шахте х рабочих, а во второй — у рабочих заняты на добыче алюминия (х и у — целые; x 0; y 0).

По условию на 2 кг алюминия приходится 1 кг никеля, то есть алюминия необходимо добывать вдвое больше.
Значит, 5х + 10у = 2 * (700 – 10х – 5у), откуда 5х + 4у = 280 (1), следовательно: 5х = 280 – 4y.
Из равенства (1) следует, что наибольшее возможное значение у равно 70 (при х = 0).
Пусть s — масса сплава (две части алюминия и одна часть никеля), которая втрое больше массы добытого никеля, следовательно:
s = 3 * (700 – 10х – 5у) = 3 * (700 – 2(280 – 4у) – 5у) = 3 * (700 – 560 + 8у – 5у) = 3 * (140 + 3у).
Так как наибольшее возможное значение у равно 70, то наибольшее значение массы сплава составляет:
s = 3 * (140 + 3 * 70) = 1050 кг
Таким образом, 70 рабочих второй шахты должны быть заняты на добыче алюминия, остальные 30 рабочих второй шахты и все 20 рабочих первой шахты — на добыче никеля.
При этом будет добыто 700 кг алюминия и 350 кг никеля, а масса сплава составит 1050 кг.
Ответ: 1050 кг.
В следующей задаче главная сложность для получения её математической модели — понять, какая величина выбирается в качестве неизвестной.
Задача 3. Рассчитать максимально возможную прибыль
Фабрика, которая производит пищевые полуфабрикаты, выпускает блинчики со следующими видами начинки: ягодная и творожная. В таблице приведены себестоимость и отпускная цена, а также производственные возможности фабрики по каждому виду продукта при полной загрузке всех мощностей только данным видом.

Для выполнения условий ассортиментности, которые предъявляются торговыми сетями, продукции каждого вида должно быть выпущено не менее 15 т. Предполагая, что вся продукция фабрики находит спрос (реализуется без остатка), найдите максимально возможную прибыль, которую может получить фабрика от производства блинчиков за один месяц.
Решение
Пусть x — доля мощностей завода, занятых под производство блинчиков с ягодной начинкой, а y — доля мощностей, занятых под производство блинчиков с творожной начинкой, следовательно: x + y = 1.
90x т — производится блинчиков с ягодной начинкой.
75y т — производится блинчиков с творожной начинкой.
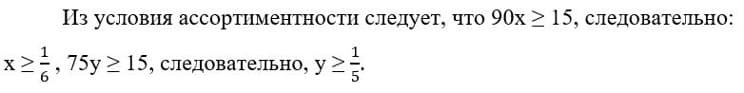
Прибыль с 1 т блинчиков с ягодной начинкой: 100 – 70 = 30 тыс. руб.
Прибыль с 1 т блинчиков с творожной начинкой: 135 – 100 = 35 тыс. руб.
Общая прибыль с произведённой за месяц продукции составит:
S (x, y) = 30 * 90х + 35 * 75y = 2700х + 2625у = 75 * (36x + 35y)
Следует найти наибольшее значение функции S (x, y) = 75 * (36x + 35y) при выполнении следующих условий:
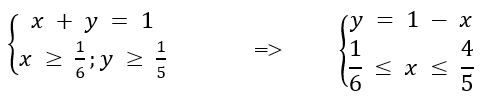
Подставляя у = 1 − x в выражение 36x + 35y, получаем:
36x + 35 * (1 − x) = x + 35
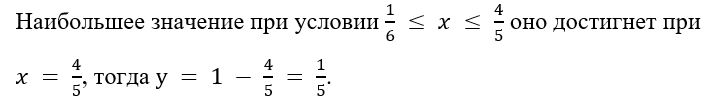
Максимально возможная прибыль завода за месяц составит:
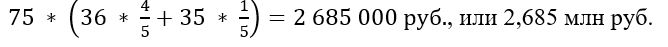
Ответ: 2,685 млн руб.
https://journal.open-broker.ru/
Не является индивидуальной инвестиционной рекомендацией | При копировании ссылка обязательна | Нашли ошибку - выделить и нажать Ctrl+Enter | Жалоба

