Продолжаем цикл статей, посвящённых решению экономических задач ЕГЭ по математике профильного уровня.
Задача на тему продажи ценных бумаг наиболее выгодным способом при имеющихся условиях была впервые предложена на ЕГЭ по математике профильного уровня 2017 года. Разберём две задачи, связанные с пенсионным фондом и ценными бумагами.
Задачи для разбора взяты из реальных вариантов ЕГЭ прошлых лет, которые размещены на популярном среди школьников и учителей сайте РЕШУ ЕГЭ.
Задача 1. Рассчитать процент r, при котором ценные бумаги можно будет продать в конце определённого года для получения наибольшей прибыли.
Пенсионный фонд владеет ценными бумагами, которые стоят t2 тыс. руб. в конце года t (t = l, 2, ...). В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счёт в банке, при этом в конце каждого следующего года сумма на счёте будет увеличиваться в 1 + r раз. Пенсионный фонд хочет продать ценные бумаги в конце такого года, чтобы в конце 25-го года сумма на его счёте была наибольшей. Расчёты показали, что для этого ценные бумаги нужно продавать строго в конце 21-го года. При каких положительных значениях r это возможно?
Решение
I способ. В конце года стоимость ценных бумаг растёт по заданному правилу. Будем считать, что одно и то же количество бумаг стоит в конце 1-го, 2-го, ..., 25-го годов соответственно (тыс. руб.):
12, 22, ..., 202, 212, 222, 232, 242, 252
Рассчитаем доход при продаже ценных бумаг в конце любого года, кроме последнего, и размещении этих денежных средств в банке под r процентов годовых. Размещённая сумма до 25-го года будет увеличиваться в 1 + r раз ежегодно и составит соответственно:
1-й год: 12 * (1 + r)24
2-й год: 22 * (1 + r)23
…
20-й год: 202 * (1 + r)5
21-й год: 212 * (1 + r)4
22-й год: 222 * (1 + r)3
23-й год: 232 * (1 + r)2
24-й год: 242 * (1 + r)
По условию задачи сумма в конце 25-го года будет наибольшей, если продажа состоялась в 21-м году, то есть наибольшая сумма равна 212 * (1 + r)4. Сравним эту сумму с соседними членами последовательности, получим два неравенства:

Внимание! Из того, что доход при продаже бумаг в конце 21-го года больше, чем доход при их продаже в конце 20-го и 22-го годов, не следует, что этот доход больше, чем при продаже в любой другой год, а именно это оговорено в условии. Поэтому решение следует дополнить.
Определим, во сколько раз увеличивается стоимость ценных бумаг по сравнению с их стоимостью в предыдущий год, если фонд не продаёт ценные бумаги, а хранит их:
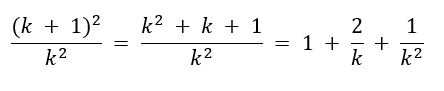
Полученное отношение убывает с ростом k, поэтому если фонд хранит ценные бумаги, не продавая их, с течением лет прирост дохода падает, приближаясь к единице. В силу этого, если момент продажи наступил в конце 21-го года, то он не мог наступить ни раньше, ни позже.
II способ. В случае продажи пенсионным фондом ценных бумаг в конце года k в конце 25-го года на его счёте будет:
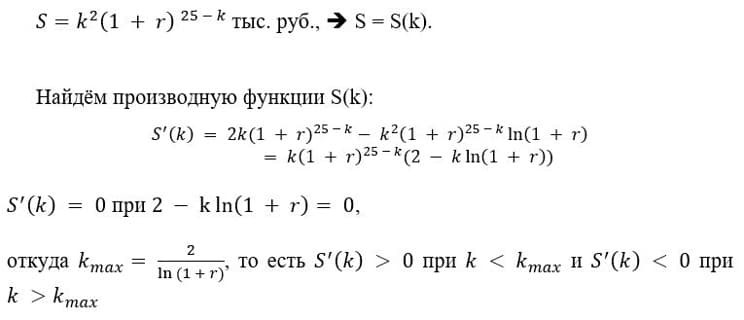
По условию задачи продавать бумаги следует в конце 21-го года. Следовательно, доход, полученный при продаже бумаг в конце 21-го года, больше, чем при их продаже в конце 20-го и 22-го года.
Согласно монотонности функции, S(k): S(21) > S(20) и S(21) < S(22), что гарантирует выполнение условия S(21) > S(k) для всех k, отличных от 21.
Необходимо и достаточно решить систему неравенств:
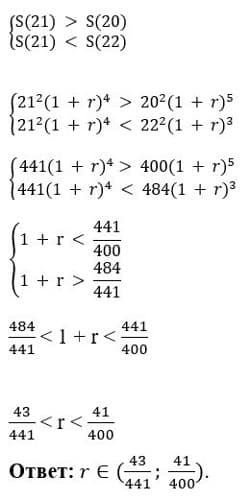
Задача 2. Рассчитать, в конце какого года надо продать акции, чтобы прибыль была максимальной
Пенсионный фонд владеет акциями, цена которых к концу года t становится равной t2 тыс. руб. (то есть к концу первого года они стоят 1 тыс. руб., к концу второго — 4 тыс. руб. и так далее), в течение 20 лет. В конце любого года можно продать акции по их рыночной цене на конец года и положить вырученные деньги в банк под 25% годовых. В конце какого года нужно продать акции, чтобы прибыль была максимальной?
Решение
I способ. Пусть акции проданы в конце года t-го за t2 тыс. руб. Вырученная при этом сумма положена в банк на оставшиеся (20 − t) лет под 25% годовых.

Точка максимума лежит в интервале (8; 10).

Задача на тему продажи ценных бумаг наиболее выгодным способом при имеющихся условиях была впервые предложена на ЕГЭ по математике профильного уровня 2017 года. Разберём две задачи, связанные с пенсионным фондом и ценными бумагами.
Задачи для разбора взяты из реальных вариантов ЕГЭ прошлых лет, которые размещены на популярном среди школьников и учителей сайте РЕШУ ЕГЭ.
Задача 1. Рассчитать процент r, при котором ценные бумаги можно будет продать в конце определённого года для получения наибольшей прибыли.
Пенсионный фонд владеет ценными бумагами, которые стоят t2 тыс. руб. в конце года t (t = l, 2, ...). В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счёт в банке, при этом в конце каждого следующего года сумма на счёте будет увеличиваться в 1 + r раз. Пенсионный фонд хочет продать ценные бумаги в конце такого года, чтобы в конце 25-го года сумма на его счёте была наибольшей. Расчёты показали, что для этого ценные бумаги нужно продавать строго в конце 21-го года. При каких положительных значениях r это возможно?
Решение
I способ. В конце года стоимость ценных бумаг растёт по заданному правилу. Будем считать, что одно и то же количество бумаг стоит в конце 1-го, 2-го, ..., 25-го годов соответственно (тыс. руб.):
12, 22, ..., 202, 212, 222, 232, 242, 252
Рассчитаем доход при продаже ценных бумаг в конце любого года, кроме последнего, и размещении этих денежных средств в банке под r процентов годовых. Размещённая сумма до 25-го года будет увеличиваться в 1 + r раз ежегодно и составит соответственно:
1-й год: 12 * (1 + r)24
2-й год: 22 * (1 + r)23
…
20-й год: 202 * (1 + r)5
21-й год: 212 * (1 + r)4
22-й год: 222 * (1 + r)3
23-й год: 232 * (1 + r)2
24-й год: 242 * (1 + r)
По условию задачи сумма в конце 25-го года будет наибольшей, если продажа состоялась в 21-м году, то есть наибольшая сумма равна 212 * (1 + r)4. Сравним эту сумму с соседними членами последовательности, получим два неравенства:

Внимание! Из того, что доход при продаже бумаг в конце 21-го года больше, чем доход при их продаже в конце 20-го и 22-го годов, не следует, что этот доход больше, чем при продаже в любой другой год, а именно это оговорено в условии. Поэтому решение следует дополнить.
Определим, во сколько раз увеличивается стоимость ценных бумаг по сравнению с их стоимостью в предыдущий год, если фонд не продаёт ценные бумаги, а хранит их:
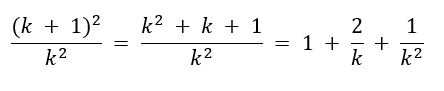
Полученное отношение убывает с ростом k, поэтому если фонд хранит ценные бумаги, не продавая их, с течением лет прирост дохода падает, приближаясь к единице. В силу этого, если момент продажи наступил в конце 21-го года, то он не мог наступить ни раньше, ни позже.
II способ. В случае продажи пенсионным фондом ценных бумаг в конце года k в конце 25-го года на его счёте будет:
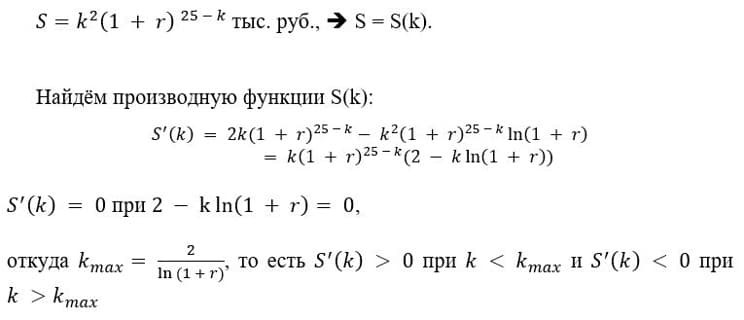
По условию задачи продавать бумаги следует в конце 21-го года. Следовательно, доход, полученный при продаже бумаг в конце 21-го года, больше, чем при их продаже в конце 20-го и 22-го года.
Согласно монотонности функции, S(k): S(21) > S(20) и S(21) < S(22), что гарантирует выполнение условия S(21) > S(k) для всех k, отличных от 21.
Необходимо и достаточно решить систему неравенств:
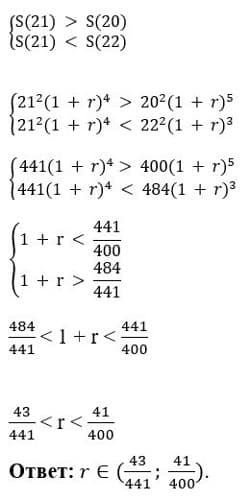
Задача 2. Рассчитать, в конце какого года надо продать акции, чтобы прибыль была максимальной
Пенсионный фонд владеет акциями, цена которых к концу года t становится равной t2 тыс. руб. (то есть к концу первого года они стоят 1 тыс. руб., к концу второго — 4 тыс. руб. и так далее), в течение 20 лет. В конце любого года можно продать акции по их рыночной цене на конец года и положить вырученные деньги в банк под 25% годовых. В конце какого года нужно продать акции, чтобы прибыль была максимальной?
Решение
I способ. Пусть акции проданы в конце года t-го за t2 тыс. руб. Вырученная при этом сумма положена в банк на оставшиеся (20 − t) лет под 25% годовых.

Точка максимума лежит в интервале (8; 10).

https://journal.open-broker.ru/
Не является индивидуальной инвестиционной рекомендацией | При копировании ссылка обязательна | Нашли ошибку - выделить и нажать Ctrl+Enter | Жалоба

