13 февраля 2018 Trade Like A Pro
Есть мнение, что Оптимальное F – это единственный лучший метод управления капиталом. Концепция «оптимального f», наверное, известна каждому валютному спекулянту, который хоть сколь-либо серьезно интересовался мани менеджментом и управлением капиталом. Главный популяризатор этой идеи, американский автор Ральф Винс, хорошо знаком с Ларри Вильямсом – легендарным фьючерсным трейдером. Сам же Винс не является практикующим трейдером, и многие ставят это ему в упрек. Сегодня мы углубимся в эту тему подробно, разберем плюсы и минусы метода оптимальной фракции, расчет, а также рассмотрим модификации подхода.
История
Ральф заметил у Келли ошибку, состоящую в том, что формула критерия Келли первоначально предназначалась для определения направления потока электронных частиц, а затем использована для блэкджека. Беда в том, что блэк-джек – это совсем не то же самое, что торговля акциями или валютами. В блэкджеке ваш потенциальный проигрыш на каждой ставке ограничен фишками, которые вы ставите, в то время как ваш потенциальный выигрыш остается всегда одинаковым в отношении поставленных фишек.
При работе на рынке размеры наших выигрышей и проигрышей постоянно меняются. Иногда мы получаем большие выигрыши, иногда крошечные. Наши убытки подчиняются тому же закону — их размер случаен. Ральф придумал формулу, подобную формуле Келли и названную им «оптимальная F», но в отличие от формулы Келли — ее можно адаптировать к торговле на рынках.
Оптимальное F (образовано от слова «фракция») – доля депозита, при которой мы будем иметь максимальную прибыль. Естественно, оптимальное f — величина не постоянная, и по мере совершения сделок значение будет меняться. То есть необходимо делать пересчет.
Если графически представить изменение конечного депозита (TWR) от размера процента использования средств (F), то зависимость будет описываться кривой:
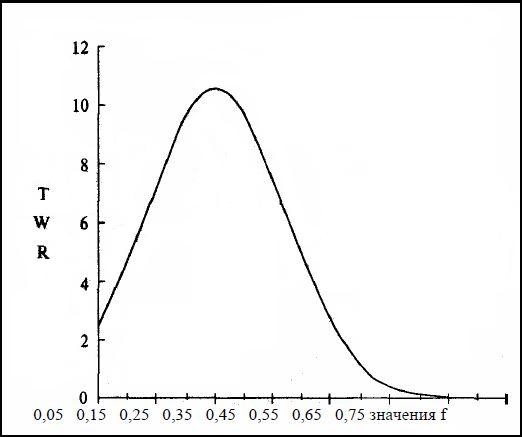
Как вы видите, при инвестировании слишком малой части депозита мы будем иметь и небольшую прибыль. Если увеличивать риски, величина конечного депозита также будет расти до определенного момента. При дальнейшем повышении рисков конечный депозит начнет падать. Этот самый момент, когда рост депозита максимальный, как раз и соответствует оптимальной f. Таким образом — вполне логично предположить, что оптимальным решением для трейдера будет использование при каждой сделке такого процента от депозита, который будет находиться в точке верхнего экстремума данной кривой.
Ну что же, давайте для наших исследований сгенерируем случайную торговую систему.
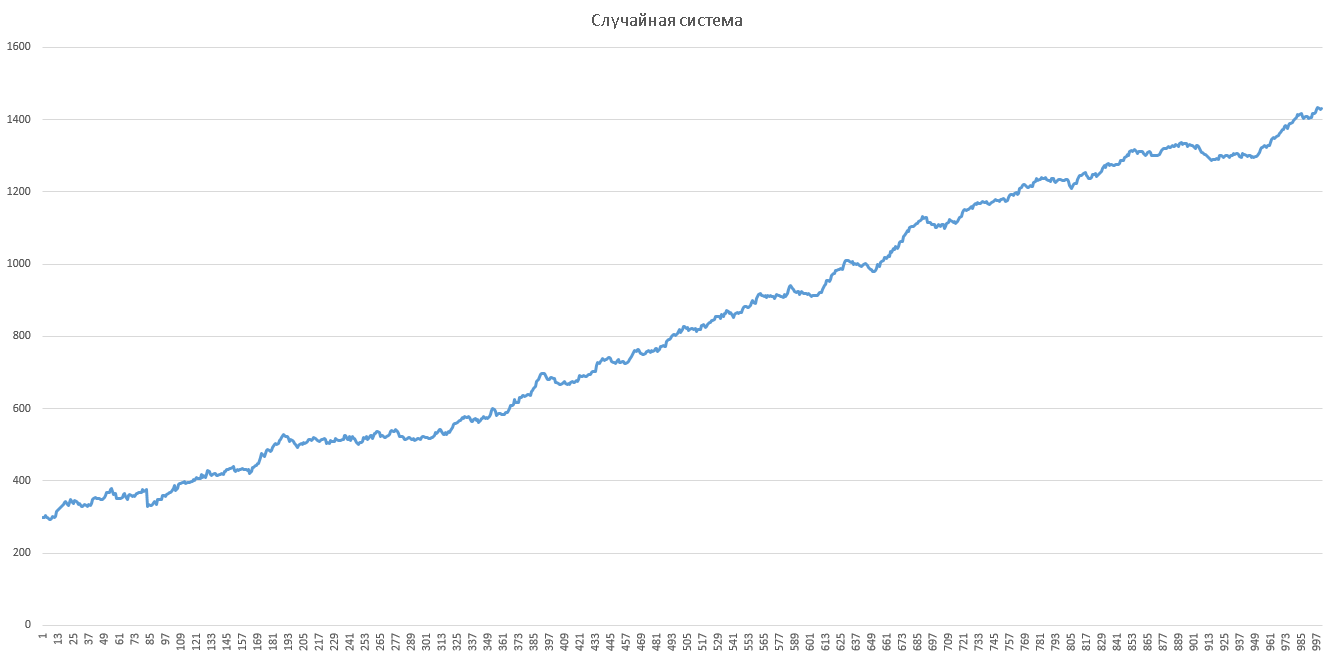
Основные статистические показатели системы получились следующими:
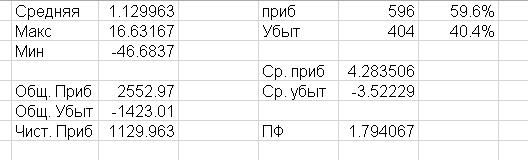
При создании ТС я воспользовался генератором случайных чисел по нормальному распределению:
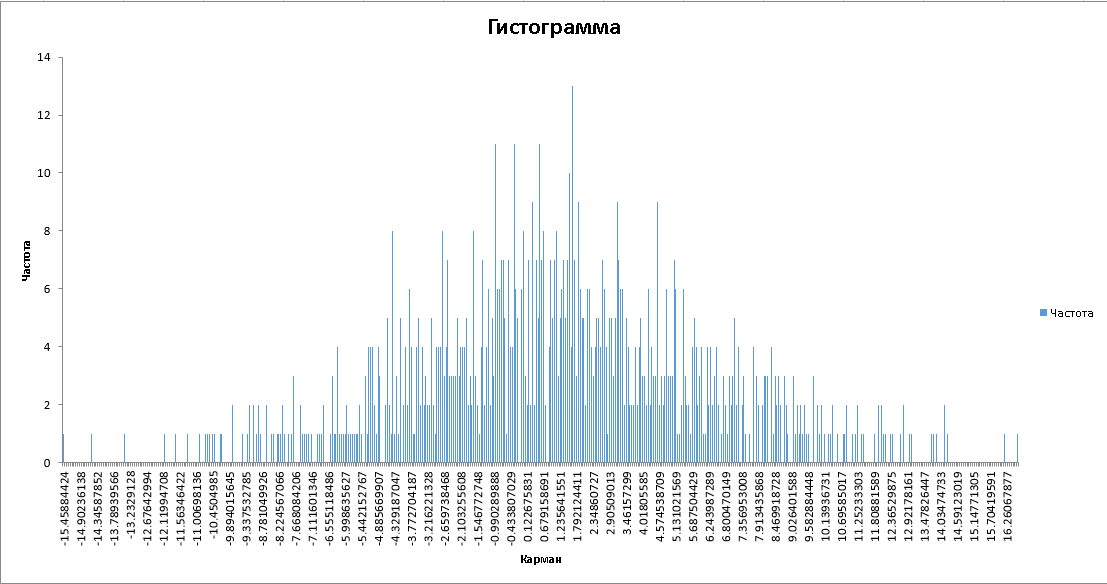
Математическое ожидание нашей торговой системы вышло немного больше 1, а стандартное отклонение около 4, что вполне сгодится для наших целей.
Теперь введем систему мани менеджмента – в каждой сделке будем рисковать определенным процентом от нашего капитала (в данном случае 3%):
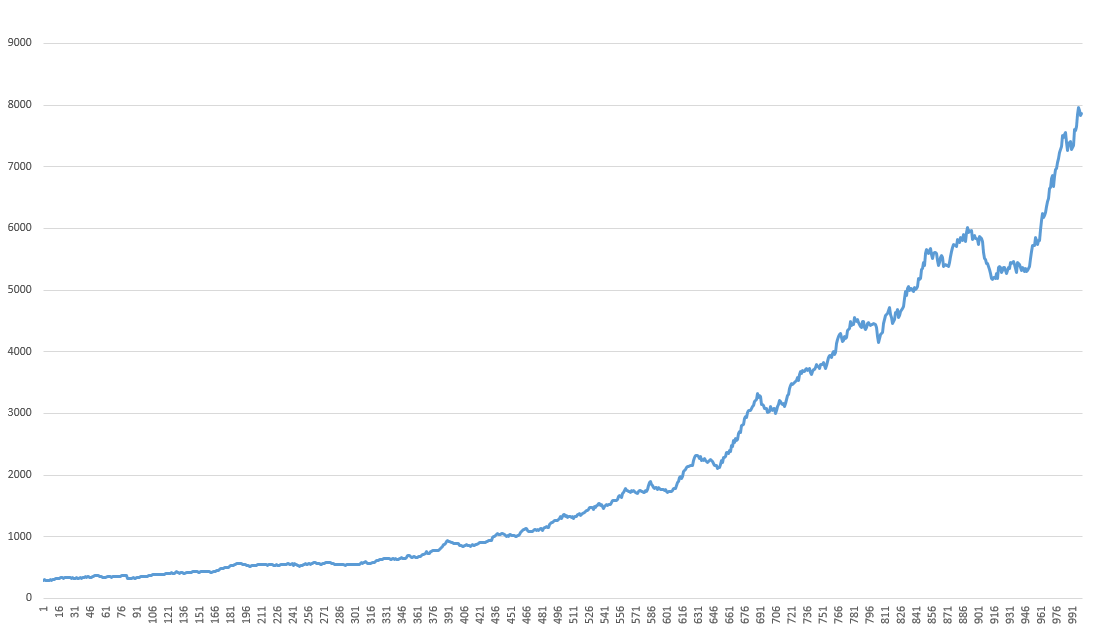
Все, что нам остается сделать – найти такой процент риска, при котором наш конечный баланс будет максимальным. Для этого мы, как обычно, можем воспользоваться встроенным в эксель функционалом поиска решений, который нашел оптимальное значение в 20%:
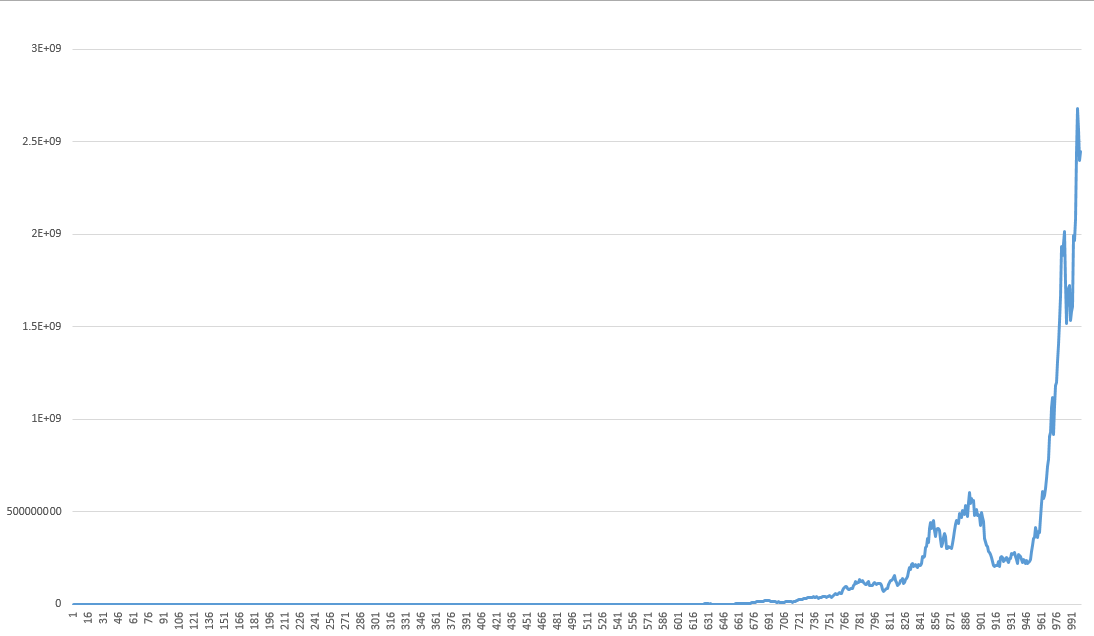
Для расчета обычно используют не величину конечного капитала, а TWR. Это показатель, характеризующий относительный конечный капитал, или, проще говоря, то, во сколько раз мы увеличили наш изначальный депозит. И в данном примере максимальный TWR составил 8159238.337 при риске 20%. Иными словами, оптимальная f конкретно для данной системы составляет 0,2.
Как вы видели на графике в самом начале, оптимальная f – это, по сути, экстремум, выше и ниже которого находятся уже неоптимальные значения TWR:

Из графика видно, что оптимальная F для нашей системы составляет 0,2 или 20% риска на сделку. При этом, если мы будем закладывать риск 21%, это даст конечный результат такой же, как если бы мы рисковали 18%. При этом если мы прибавим буквально еще один процент и будем рисковать 22%, счет будет слит.
Расчет оптимального f
Давайте подробнее остановимся на расчете оптимального f. Для расчета оптимального f необходимо сначала вычислить прибыль за определенный период – HPR.
Далее рассчитывается TWR, как произведение всех HPR, то есть:
Ну, и в итоге, мы вычисляем среднее геометрическое HPR (G), которое рассчитывается как корень в степени n от TWR: G=TWR^(1/n), где n — общее количество сделок.
Все параметры для вычисления у нас известны, кроме значения f. Ваша задача – пошагово перебирать f от 0,01 до 1 таким образом, чтобы найти максимальное G. При этом f, при котором G максимально, и будет оптимальным f.
Опасность оптимальной f
Оптимальность f таит в себе большую опасность. Вы наверняка обратили внимание, что в нашем примере оптимальная f составила 20 и при этом при риске 22% мы просто сливаем все подчистую. Отклонение всего на 10% от оптимального значения приводит к фатальным для вашего счета последствиям.
Но дело в том, что когда мы обсуждаем TWR, то допускаем использование дробных лотов. Например, вы можете торговать 5,4789 лотами, если именно это требуется в какой-либо момент. Расчет TWR допускает дробные лоты, чтобы его значение всегда было одинаково для данного набора торговых результатов вне зависимости от их последовательности. Вы можете усомниться в правильности такого подхода, поскольку при реальной торговле это невыполнимо. В реальной жизни вы не можете торговать подобными дробными лотами. Этот аргумент правильный. Но если мы будем использовать только круглые значения лотов для расчета, неправильным станет сам расчет. При этом, чем ближе вы находитесь к оптимальному f, тем лучше. И с другой стороны, немного промахнувшись, вы сольете свой счет.
Очевидно, что чем больше капитализация счета, тем более точно вы сможете придерживаться оптимального f, так как сумма в долларах, требуемая под один лот, составит меньший процент от общего баланса.
Многие профессионалы используют фиксированную долю при торговле, но эта доля никогда не была даже близко такой высокой, как оптимальная f. Дело в том, что Ральф Винс, бесспорно, профессионал своего дела и отличный теоретик. Но сильно напрягает одна деталь. Дело в том, что как бы мы ни пытались предсказать размер максимальной убыточной сделки, всегда есть немалая вероятность того, что в будущем эта величина может быть превышена. Мы более-менее хорошо можем предсказывать средние величины вроде математического ожидания или средней прибыльной сделки при условии достаточного количества статистики. Но максимально убыточная, максимально прибыльная сделка, максимальная просадка – все это довольно плохо предсказуемые величины. Именно поэтому от оптимального f не так уж и много толку, ведь немного ошибившись в этой самой максимальной убыточной сделке мы ошибемся в оптимальном f. А ошибившись в оптимальном f всего на процент-другой мы получаем маржин колл.
И все же, нельзя сказать, что эта формула совсем уж бесполезна. Более того, в некоторых частных случаях, например, для бинарных опционов или для систем с жесткими стопами и профитами (правда, такие системы, на мой взгляд, сами по себе неоптимальные), она является точной. Поэтому, если вы точно знаете ваш максимальный убыток, данный способ управления капиталом вам вполне подойдет.
Давайте проверим мою точку зрения – сгенерируем еще 1000 сделок с теми же характеристиками – средним значением 1 и стандартным отклонением 5. При этом мы будем использовать ту же оптимальную f, равную 20%.
Добавим 1000 сделок:
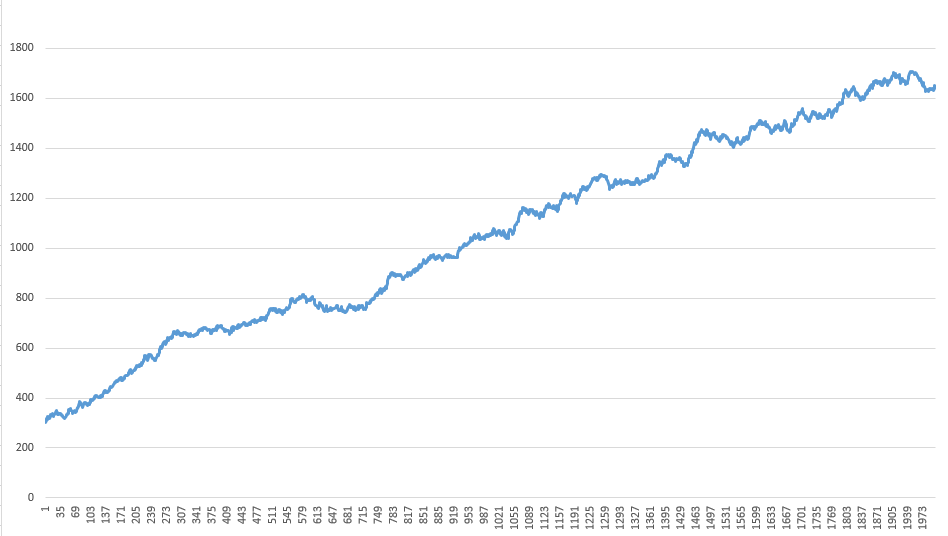
И посмотрим на торговлю при том же риске 20%:
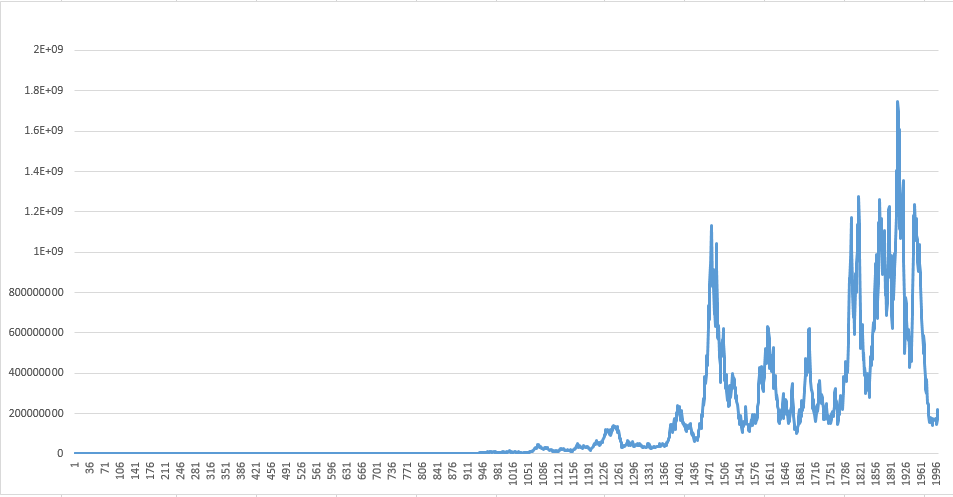
Как видите, оптимальным этот уровень риска уже не назовешь. Он просто на просто изменился.
Допустим, оптимальная фракция для предыдущих 100 сделок составляла 15%, в последующих 100 сделках эта доля может оказаться равной 9%. Если для предыдущих 100 сделок оптимальной была доля 15% и вы решили провести 100 следующих сделок с той же фракцией, то вы вполне можете ошибиться и легко выйти за пределы суммы на вашем торговом счете.
Практическое применение стратегии оптимальной фракции оптимизирует прошлые сделки. Поэтому очередная сделка сразу попадает в последовательность, и оптимальная доля повторно оптимизируется. И будет оптимизироваться при заключении каждой сделки. То есть в реальной торговле вы после каждой сделки должны будете заново рассчитывать оптимальную фракцию.
Кроме того, торговля совершенно непредсказуема, несмотря на все показатели, которые можно вычислить на основе имеющейся статистики. С помощью логики мы можем всего лишь сделать определенные выводы относительно разумных ожиданий и вероятностей. Никакое математическое выражение не может нам гарантировать, что из N количества сделок 50% будут прибыльными, а остальные 50% принесут убытки. Торговые стратегии формируются на основе логики и в значительной степени рыночной статистики. Поведение рынка меняется. То, что вчера представлялось благоприятным, сегодня может стать опасным.
Найдется еще сотня других и достаточно логичных причин, почему метод оптимальной фракции безупречен с математической точки зрения, но оказывается довольно опасным в практическом применении. Однако некоторые моменты, которые я анализировал выше, показывают, что нет смысла продолжать обсуждение этой темы далее. Риск сам по себе является достаточно веским аргументом против того, чтобы использовать метод оптимальной фракции. Если вы считаете, что сумеете справиться с риском, то убедитесь в том, что хорошо понимаете этот метод, прежде чем начнете применять его в своей торговой практике.
Итак, основная проблема оптимальной фракции, как вы уже поняли, состоит в ее привязке к максимальной убыточной сделке. В случае использования жестких стоп лоссов это не страшно, но, когда выходы из сделок в убыточной зоне в основном происходят по сигналам с рынка, оптимальная f становится не оптимальной и завышенной, что грозит сливом депозита или же серьезными потерями.
Предположим, в течение торгового дня произошло событие, вызвавшее на рынке шок, и до этого шока волатильность была достаточно низкой. Само собой, в таких условиях ваша оптимальная f будет очень высока и велика вероятность того, что вы в этот самый неудачный день войдете в рынок с риском процентов тридцать, который обернется в итоге во все 50% убытка.
Именно по перечисленным выше причинам и используют различные модификации метода оптимального f, с которыми мы сейчас и познакомимся.
Разбавленная оптимальная фракция
Для того, чтобы избежать слива депозита при небольшом отклонении, был предложен метод разбавления оптимальной фракции (diluted optimal f). По сути — разбавленная оптимальная f является процентной частью от оптимальной f. Данная техника используется, во-первых, для того, чтобы в результате оптимизации на исторических данных оптимальная величина капитала не была переоценена и, во-вторых, для того, чтобы трейдер мог сам регулировать свой риск (количество используемого в торговле капитала) при использовании оптимальной f.
Формула расчета очень проста:
Вы можете, например, задать X = 0.5 и быть уверенными, что половина рассчитанной на истории оптимальной f вряд ли когда-либо превысит в будущем реальную оптимальную f.
Недостатки тут те же, что и при оптимальном f, но вероятность переоценки риска, которая может привести к сливу счета, в этом случае существенно ниже.
Безопасная фракция
Безопасная фракция (Secure f) является частью капитала, вовлеченного в каждую сделку при ограничении просадки и максимизации прибыли. Безопасная фракция имеет некоторые преимущества перед оптимальной фракцией, поскольку опирается не на максимальный убыток, а на некоторые другие факторы. Стратегия похожа на технику оптимальной f c той лишь разницей, что при использовании оптимальной f ваша стратегия оптимизируется по прибыли с учетом максимальной просадки за расчетный период исторических данных, а при использовании безопасной f вы сами ограничиваете эту просадку.
Расчет тоже довольно прост. Вместо максимальной убыточной сделки мы просто используем максимальную просадку в валюте. Работа по методу безопасной фракции менее рискованная, чем при использовании оптимальной фракции, но рост капитала будет проходить существенно медленнее, особенно на небольших депозитах.
Заключение
Сегодня мы познакомились с такими методами мани менеджмента, как оптимальная и безопасная фракция. С точки зрения логики и математики оба этих метода расчета риска выглядят очень привлекательно. Однако, как мы сегодня убедились, и у этих методов есть свои недостатки. Немалое количество трейдеров на рынке форекс считает, что рисковать нужно по максимуму и направляют свои усилия именно на максимальный прирост депозита. Иными словами, существует очень большое количество так называемых «разгонщиков депозитов». И именно для них такие методы управления капиталом, как оптимальная фракция и критерий Келли могут показаться отличным решением.
Тем же трейдерам, которые также не против высоких рисков, но при этом не любят терять депозиты слишком часто, я могу порекомендовать использовать более легкую безопасную фракцию или же разбавленную оптимальную фракцию, которые избавят от вероятности применения слишком большого риска.
История
Ральф заметил у Келли ошибку, состоящую в том, что формула критерия Келли первоначально предназначалась для определения направления потока электронных частиц, а затем использована для блэкджека. Беда в том, что блэк-джек – это совсем не то же самое, что торговля акциями или валютами. В блэкджеке ваш потенциальный проигрыш на каждой ставке ограничен фишками, которые вы ставите, в то время как ваш потенциальный выигрыш остается всегда одинаковым в отношении поставленных фишек.
При работе на рынке размеры наших выигрышей и проигрышей постоянно меняются. Иногда мы получаем большие выигрыши, иногда крошечные. Наши убытки подчиняются тому же закону — их размер случаен. Ральф придумал формулу, подобную формуле Келли и названную им «оптимальная F», но в отличие от формулы Келли — ее можно адаптировать к торговле на рынках.
Оптимальное F (образовано от слова «фракция») – доля депозита, при которой мы будем иметь максимальную прибыль. Естественно, оптимальное f — величина не постоянная, и по мере совершения сделок значение будет меняться. То есть необходимо делать пересчет.
Если графически представить изменение конечного депозита (TWR) от размера процента использования средств (F), то зависимость будет описываться кривой:

Как вы видите, при инвестировании слишком малой части депозита мы будем иметь и небольшую прибыль. Если увеличивать риски, величина конечного депозита также будет расти до определенного момента. При дальнейшем повышении рисков конечный депозит начнет падать. Этот самый момент, когда рост депозита максимальный, как раз и соответствует оптимальной f. Таким образом — вполне логично предположить, что оптимальным решением для трейдера будет использование при каждой сделке такого процента от депозита, который будет находиться в точке верхнего экстремума данной кривой.
Ну что же, давайте для наших исследований сгенерируем случайную торговую систему.

Основные статистические показатели системы получились следующими:

При создании ТС я воспользовался генератором случайных чисел по нормальному распределению:

Математическое ожидание нашей торговой системы вышло немного больше 1, а стандартное отклонение около 4, что вполне сгодится для наших целей.
Теперь введем систему мани менеджмента – в каждой сделке будем рисковать определенным процентом от нашего капитала (в данном случае 3%):

Все, что нам остается сделать – найти такой процент риска, при котором наш конечный баланс будет максимальным. Для этого мы, как обычно, можем воспользоваться встроенным в эксель функционалом поиска решений, который нашел оптимальное значение в 20%:

Для расчета обычно используют не величину конечного капитала, а TWR. Это показатель, характеризующий относительный конечный капитал, или, проще говоря, то, во сколько раз мы увеличили наш изначальный депозит. И в данном примере максимальный TWR составил 8159238.337 при риске 20%. Иными словами, оптимальная f конкретно для данной системы составляет 0,2.
Как вы видели на графике в самом начале, оптимальная f – это, по сути, экстремум, выше и ниже которого находятся уже неоптимальные значения TWR:

Из графика видно, что оптимальная F для нашей системы составляет 0,2 или 20% риска на сделку. При этом, если мы будем закладывать риск 21%, это даст конечный результат такой же, как если бы мы рисковали 18%. При этом если мы прибавим буквально еще один процент и будем рисковать 22%, счет будет слит.
Расчет оптимального f
Давайте подробнее остановимся на расчете оптимального f. Для расчета оптимального f необходимо сначала вычислить прибыль за определенный период – HPR.
HPR=1+f*(-сделка/наибольший проигрыш), где:
f — риск в каждой сделке;
сделка — прибыль или убыток в конкретной сделке (в случае убытка выражение в скобках у вас получится отрицательным, как и итоговое значение);
наибольший проигрыш — наибольший убыток за сделку (отрицательное число).Далее рассчитывается TWR, как произведение всех HPR, то есть:
TWR = HPR1*HPR2*….*HPRn, где n – последняя сделка в вашей выборке.Ну, и в итоге, мы вычисляем среднее геометрическое HPR (G), которое рассчитывается как корень в степени n от TWR: G=TWR^(1/n), где n — общее количество сделок.
Все параметры для вычисления у нас известны, кроме значения f. Ваша задача – пошагово перебирать f от 0,01 до 1 таким образом, чтобы найти максимальное G. При этом f, при котором G максимально, и будет оптимальным f.
Опасность оптимальной f
Оптимальность f таит в себе большую опасность. Вы наверняка обратили внимание, что в нашем примере оптимальная f составила 20 и при этом при риске 22% мы просто сливаем все подчистую. Отклонение всего на 10% от оптимального значения приводит к фатальным для вашего счета последствиям.
Но дело в том, что когда мы обсуждаем TWR, то допускаем использование дробных лотов. Например, вы можете торговать 5,4789 лотами, если именно это требуется в какой-либо момент. Расчет TWR допускает дробные лоты, чтобы его значение всегда было одинаково для данного набора торговых результатов вне зависимости от их последовательности. Вы можете усомниться в правильности такого подхода, поскольку при реальной торговле это невыполнимо. В реальной жизни вы не можете торговать подобными дробными лотами. Этот аргумент правильный. Но если мы будем использовать только круглые значения лотов для расчета, неправильным станет сам расчет. При этом, чем ближе вы находитесь к оптимальному f, тем лучше. И с другой стороны, немного промахнувшись, вы сольете свой счет.
Очевидно, что чем больше капитализация счета, тем более точно вы сможете придерживаться оптимального f, так как сумма в долларах, требуемая под один лот, составит меньший процент от общего баланса.
Многие профессионалы используют фиксированную долю при торговле, но эта доля никогда не была даже близко такой высокой, как оптимальная f. Дело в том, что Ральф Винс, бесспорно, профессионал своего дела и отличный теоретик. Но сильно напрягает одна деталь. Дело в том, что как бы мы ни пытались предсказать размер максимальной убыточной сделки, всегда есть немалая вероятность того, что в будущем эта величина может быть превышена. Мы более-менее хорошо можем предсказывать средние величины вроде математического ожидания или средней прибыльной сделки при условии достаточного количества статистики. Но максимально убыточная, максимально прибыльная сделка, максимальная просадка – все это довольно плохо предсказуемые величины. Именно поэтому от оптимального f не так уж и много толку, ведь немного ошибившись в этой самой максимальной убыточной сделке мы ошибемся в оптимальном f. А ошибившись в оптимальном f всего на процент-другой мы получаем маржин колл.
И все же, нельзя сказать, что эта формула совсем уж бесполезна. Более того, в некоторых частных случаях, например, для бинарных опционов или для систем с жесткими стопами и профитами (правда, такие системы, на мой взгляд, сами по себе неоптимальные), она является точной. Поэтому, если вы точно знаете ваш максимальный убыток, данный способ управления капиталом вам вполне подойдет.
Давайте проверим мою точку зрения – сгенерируем еще 1000 сделок с теми же характеристиками – средним значением 1 и стандартным отклонением 5. При этом мы будем использовать ту же оптимальную f, равную 20%.
Добавим 1000 сделок:

И посмотрим на торговлю при том же риске 20%:

Как видите, оптимальным этот уровень риска уже не назовешь. Он просто на просто изменился.
Допустим, оптимальная фракция для предыдущих 100 сделок составляла 15%, в последующих 100 сделках эта доля может оказаться равной 9%. Если для предыдущих 100 сделок оптимальной была доля 15% и вы решили провести 100 следующих сделок с той же фракцией, то вы вполне можете ошибиться и легко выйти за пределы суммы на вашем торговом счете.
Практическое применение стратегии оптимальной фракции оптимизирует прошлые сделки. Поэтому очередная сделка сразу попадает в последовательность, и оптимальная доля повторно оптимизируется. И будет оптимизироваться при заключении каждой сделки. То есть в реальной торговле вы после каждой сделки должны будете заново рассчитывать оптимальную фракцию.
Кроме того, торговля совершенно непредсказуема, несмотря на все показатели, которые можно вычислить на основе имеющейся статистики. С помощью логики мы можем всего лишь сделать определенные выводы относительно разумных ожиданий и вероятностей. Никакое математическое выражение не может нам гарантировать, что из N количества сделок 50% будут прибыльными, а остальные 50% принесут убытки. Торговые стратегии формируются на основе логики и в значительной степени рыночной статистики. Поведение рынка меняется. То, что вчера представлялось благоприятным, сегодня может стать опасным.
Найдется еще сотня других и достаточно логичных причин, почему метод оптимальной фракции безупречен с математической точки зрения, но оказывается довольно опасным в практическом применении. Однако некоторые моменты, которые я анализировал выше, показывают, что нет смысла продолжать обсуждение этой темы далее. Риск сам по себе является достаточно веским аргументом против того, чтобы использовать метод оптимальной фракции. Если вы считаете, что сумеете справиться с риском, то убедитесь в том, что хорошо понимаете этот метод, прежде чем начнете применять его в своей торговой практике.
Итак, основная проблема оптимальной фракции, как вы уже поняли, состоит в ее привязке к максимальной убыточной сделке. В случае использования жестких стоп лоссов это не страшно, но, когда выходы из сделок в убыточной зоне в основном происходят по сигналам с рынка, оптимальная f становится не оптимальной и завышенной, что грозит сливом депозита или же серьезными потерями.
Предположим, в течение торгового дня произошло событие, вызвавшее на рынке шок, и до этого шока волатильность была достаточно низкой. Само собой, в таких условиях ваша оптимальная f будет очень высока и велика вероятность того, что вы в этот самый неудачный день войдете в рынок с риском процентов тридцать, который обернется в итоге во все 50% убытка.
Именно по перечисленным выше причинам и используют различные модификации метода оптимального f, с которыми мы сейчас и познакомимся.
Разбавленная оптимальная фракция
Для того, чтобы избежать слива депозита при небольшом отклонении, был предложен метод разбавления оптимальной фракции (diluted optimal f). По сути — разбавленная оптимальная f является процентной частью от оптимальной f. Данная техника используется, во-первых, для того, чтобы в результате оптимизации на исторических данных оптимальная величина капитала не была переоценена и, во-вторых, для того, чтобы трейдер мог сам регулировать свой риск (количество используемого в торговле капитала) при использовании оптимальной f.
Формула расчета очень проста:
Diluted optimal f = Optimal f * X, гдеХ — выбранный вами процент от оптимальной fВы можете, например, задать X = 0.5 и быть уверенными, что половина рассчитанной на истории оптимальной f вряд ли когда-либо превысит в будущем реальную оптимальную f.
Недостатки тут те же, что и при оптимальном f, но вероятность переоценки риска, которая может привести к сливу счета, в этом случае существенно ниже.
Безопасная фракция
Безопасная фракция (Secure f) является частью капитала, вовлеченного в каждую сделку при ограничении просадки и максимизации прибыли. Безопасная фракция имеет некоторые преимущества перед оптимальной фракцией, поскольку опирается не на максимальный убыток, а на некоторые другие факторы. Стратегия похожа на технику оптимальной f c той лишь разницей, что при использовании оптимальной f ваша стратегия оптимизируется по прибыли с учетом максимальной просадки за расчетный период исторических данных, а при использовании безопасной f вы сами ограничиваете эту просадку.
Расчет тоже довольно прост. Вместо максимальной убыточной сделки мы просто используем максимальную просадку в валюте. Работа по методу безопасной фракции менее рискованная, чем при использовании оптимальной фракции, но рост капитала будет проходить существенно медленнее, особенно на небольших депозитах.
Заключение
Сегодня мы познакомились с такими методами мани менеджмента, как оптимальная и безопасная фракция. С точки зрения логики и математики оба этих метода расчета риска выглядят очень привлекательно. Однако, как мы сегодня убедились, и у этих методов есть свои недостатки. Немалое количество трейдеров на рынке форекс считает, что рисковать нужно по максимуму и направляют свои усилия именно на максимальный прирост депозита. Иными словами, существует очень большое количество так называемых «разгонщиков депозитов». И именно для них такие методы управления капиталом, как оптимальная фракция и критерий Келли могут показаться отличным решением.
Тем же трейдерам, которые также не против высоких рисков, но при этом не любят терять депозиты слишком часто, я могу порекомендовать использовать более легкую безопасную фракцию или же разбавленную оптимальную фракцию, которые избавят от вероятности применения слишком большого риска.
Не является индивидуальной инвестиционной рекомендацией | При копировании ссылка обязательна | Нашли ошибку - выделить и нажать Ctrl+Enter | Жалоба

