5 декабря 2018 Trade Like A Pro
Вряд ли вы найдете хоть одного новичка на рынке Forex, который не знал бы, что такое фрактал. Да и вне рынка о таком понятии слышало немало людей. Фракталы известны уже почти век, хорошо изучены и имеют многочисленные приложения в жизни. В основе этого явления лежит очень простая идея: бесконечное по красоте и разнообразию множество фигур можно получить из относительно простых конструкций при помощи всего двух операций — копирования и масштабирования.
Фракталы применяются на финансовых рынках уже довольно давно – даже в классических торговых стратегиях есть упоминания о них. Например, известная торговая стратегия Билла Вильямса Profitunity использует фракталы как один из элементов системы. Сегодня этот индикатор — герой нашего обзора: мы узнаем историю его появления, посмотрим, какие бывают фракталы, а в теме на форуме вы сможете ознакомиться более чем с сотней разновидностей этого индикатора)
Что такое фрактал?
У понятия «фрактал» нет строгого определения. Поэтому это слово не является математическим термином. Обычно так называют геометрическую фигуру, которая удовлетворяет одному или нескольким из следующих свойств:
— обладает сложной структурой при любом увеличении;
— является (приближенно) самоподобной;
— обладает дробной хаусдорфовой (фрактальной) размерностью, которая больше топологической;
— может быть построена рекурсивными процедурами.
История возникновения
На рубеже XIX и XX веков изучение фракталов носило скорее эпизодический, нежели систематический характер. Раньше математики, в основном, изучали объекты, которые поддавались исследованию при помощи общих методов и теорий.
В 1872 году немецкий математик Карл Вейерштрасс построил пример непрерывной функции, которая нигде не дифференцируема. Однако его построение было целиком абстрактно и трудно для восприятия. Поэтому в 1904 году швед Хельге фон Кох придумал непрерывную кривую, которая нигде не имеет касательной, причем ее довольно просто нарисовать. Оказалось, что она обладает свойствами фрактала. Один из вариантов этой кривой носит название «снежинка Коха».
Идеи самоподобия фигур подхватил француз Поль Пьер Леви, будущий наставник Бенуа Мандельброта. В 1938 году вышла его статья «Плоские и пространственные кривые и поверхности, состоящие из частей, подобных целому», в которой описан еще один фрактал — С-кривая Леви. Все эти вышеперечисленные фракталы можно условно отнести к одному классу конструктивных (геометрических) фракталов.
Другой класс — динамические, или алгебраические фракталы, к которым относится и множество Мандельброта. Первые исследования в этом направлении относятся к началу XX века и связаны с именами французских математиков Гастона Жюлиа и Пьера Фату. В 1918 году вышел почти двухсотстраничный труд Жюлиа, посвященный итерациям комплексных рациональных функций, в котором описаны множества Жюлиа — целое семейство фракталов, близко связанных с множеством Мандельброта. Этот труд был удостоен приза Французской академии, однако в нем не содержалось ни одной иллюстрации, так что оценить красоту открытых объектов было невозможно. Несмотря на то, что это работа прославила Жюлиа среди математиков того времени, о ней довольно быстро забыли.
Вновь внимание к работам Жюлиа и Фату обратилось лишь полвека спустя, с появлением компьютеров: именно они сделали видимыми богатство и красоту мира фракталов. Ведь Фату никогда не мог посмотреть на изображения, которые мы сейчас знаем, как изображения множества Мандельброта, потому что необходимое количество вычислений невозможно провести вручную. Первым, кто использовал для этого компьютер, был Бенуа Мандельброт.
В 1982 году вышла книга Мандельброта «Фрактальная геометрия природы», в которой автор собрал и систематизировал практически всю имевшуюся на тот момент информацию о фракталах и в легкой и доступной манере изложил ее. Основной упор в своем изложении Мандельброт сделал не на тяжеловесные формулы и математические конструкции, а на геометрическую интуицию читателей.
Благодаря иллюстрациям, полученным при помощи компьютера и историческим байкам, которыми автор умело разбавил научную составляющую монографии, книга стала бестселлером, а фракталы стали известны широкой публике. Их успех среди не математиков во многом обусловлен тем, что с помощью весьма простых конструкций и формул, которые способен понять и старшеклассник, получаются удивительные по сложности и красоте изображения.
Когда персональные компьютеры стали достаточно мощными, то появилось даже целое направление в искусстве — фрактальная живопись, причем заниматься ею мог практически любой владелец компьютера. Сейчас в интернете можно легко найти множество сайтов, посвященных этой тематике.
После этого краткого экскурса в историю давайте, теперь, ознакомимся с классификацией типов фракталов на сегодняшний день.
Геометрические фракталы
Именно с них, как вы уже поняли, и начиналась история фракталов. Этот тип фракталов получается путем простых геометрических построений. Сначала изображается основа. Затем некоторые части основы заменяются на фрагмент. На каждом следующем этапе части уже построенной фигуры, аналогичные замененным частям основы, вновь заменяются на фрагмент, взятый в подходящем масштабе. Всякий раз масштаб уменьшается. Когда изменения становятся визуально незаметными, считают, что построенная фигура хорошо приближает фрактал и дает представление о его форме. Для получения самого фрактала нужно бесконечное число этапов. Меняя основу и фрагмент — можно получить много разных геометрических фракталов.
Геометрические фракталы хороши тем, что, с одной стороны, являются предметом достаточного серьезного научного изучения, а с другой стороны — их можно увидеть. Даже человек, далекий от математики, найдет в них что-то для себя. Такое сочетание редко в современной математике, где все объекты задаются с помощью непонятных слов и символов.
Многие геометрические фракталы можно нарисовать буквально на листочке бумаги в клетку. Важно понимать, что все получаемые изображения являются лишь конечными приближениями бесконечных, по своей сути, фракталов. Но всегда можно нарисовать такое приближение, что глаз не будет различать совсем мелкие детали и наше воображение сможет создать верную картину фрактала.
Например, имея достаточно большой лист миллиметровой бумаги и запас свободного времени, можно вручную нарисовать такое точное приближение к ковру Серпинского, что с расстояния в несколько метров невооруженный глаз будет воспринимать его как настоящий фрактал. Компьютер позволит сэкономить время и бумагу и при этом еще увеличить точность рисования.
Снежинка Коха
Это один из самых первых исследованных учеными фракталов. Снежинка получается из трех копий кривой Коха, которая впервые появилась в статье шведского математика Хельге фон Коха в 1904 году. Эта кривая была придумана как пример непрерывной линии, к которой нельзя провести касательную ни в одной точке. Линии с таким свойством были известны и раньше, но кривая Коха замечательна простотой своей конструкции.
Кривая Коха непрерывна, но нигде не дифференцируема. Грубо говоря, именно для этого она и была придумана — как пример такого рода математических «уродцев».
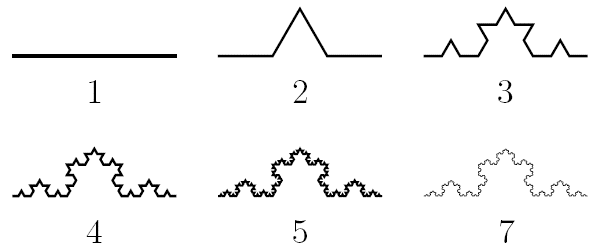
Кривая Коха имеет бесконечную длину. Пусть длина исходного отрезка равна 1. На каждом шаге построения мы заменяем каждый из составляющих линию отрезков на ломаную, которая в 4/3 раза длиннее. Значит, и длина всей ломаной на каждом шаге умножается на 4/3: длина линии с номером n равна (4/3)n–1. Поэтому предельной линии ничего не остается, кроме как быть бесконечно длинной.



Снежинка Коха ограничивает конечную площадь. И это при том, что ее периметр бесконечен. Это свойство может показаться парадоксальным, но оно очевидно — снежинка полностью помещается в круг, поэтому ее площадь заведомо ограничена. Площадь можно посчитать, и для этого даже не нужно особых знаний — формулы площади треугольника и суммы геометрической прогрессии проходят в школе.
Снежинка Коха «наоборот»
Снежинка Коха «наоборот» получается, если строить кривые Коха внутрь исходного равностороннего треугольника.

Линии Чезаро
Вместо равносторонних треугольников используются равнобедренные с углом при основании от 60° до 90°. На рисунке ниже угол равен 88°.
Квадратный вариант
Тут достраиваются квадраты.
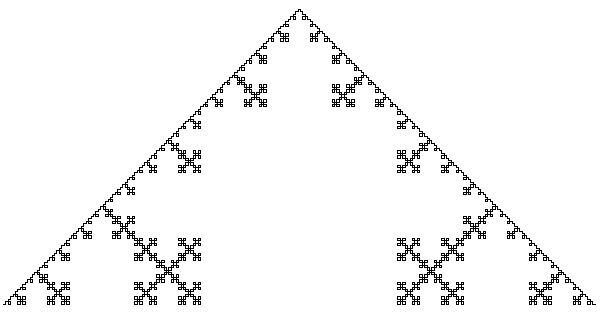
Пирамида Коха
Т-квадрат
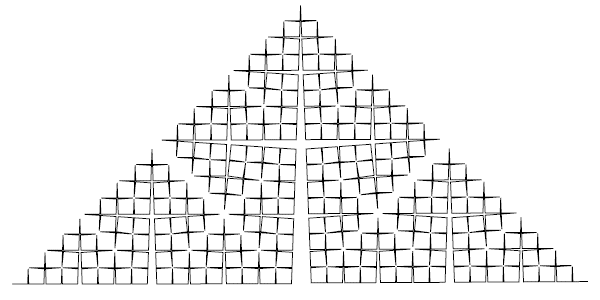
Построение начинается с единичного квадрата. Первый шаг: закрасить в центре белым цветом квадрат со стороной 1/2. Затем нужно мысленно разделить квадрат на 4 одинаковых и в центре каждого из них закрасить квадрат со стороной 1/4. Дальше каждый из этих 4 квадратов снова делится на 4 части, всего получится 16 квадратиков, и с каждым из них нужно проделать то же самое. И так далее.

Фрактальная размерность закрашена белым и равна log24 = 2. Она всюду плотна в исходном квадрате. Это означает, что какую бы точку квадрата мы ни взяли, в любой, сколь угодно малой ее окрестности найдутся закрашенные точки. То есть в итоге почти всё стало белым — площадь остатка равна 0, а фрактал занимает площадь 1. Зато длина границы закрашенной части бесконечна.
H-фрактал
Всё начинается с фигуры в виде буквы Н, у которой вертикальные и горизонтальные отрезки равны. Затем к каждому из 4 концов фигуры пририсовывается ее копия, уменьшенная в два раза. К каждому концу (их уже 16) пририсовывается копия буквы Н, уменьшенная уже в 4 раза. И так далее. В пределе получится фрактал, который визуально почти заполняет некоторый квадрат. Н-фрактал всюду плотен в нём. То есть в любой окрестности любой точки квадрата найдутся точки фрактала. Очень похоже на то, что происходит с Т-квадратом. Это не случайно, ведь, если присмотреться, видно, что каждая буква Н содержится в своем маленьком квадратике, который был дорисован на таком же шаге.
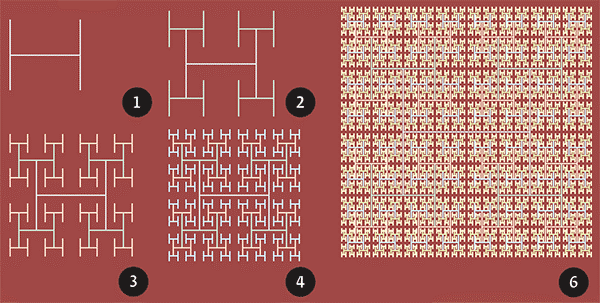
Можно сказать (и доказать), что Н-фрактал заполняет свой квадрат (англ. space-filling curve). Поэтому его фрактальная размерность равна 2. Суммарная длина всех отрезков при этом бесконечна.
Принцип построения Н-фрактала применяют при производстве электронных микросхем: если нужно, чтобы в сложной схеме большое число элементов получило один и тот же сигнал одновременно, то их можно расположить в концах отрезков подходящей итерации Н-фрактала и соединить соответствующим образом.
Дерево Мандельброта
Дерево Мандельброта получается, если рисовать толстые буквы Н, состоящие из прямоугольников, а не из отрезков:
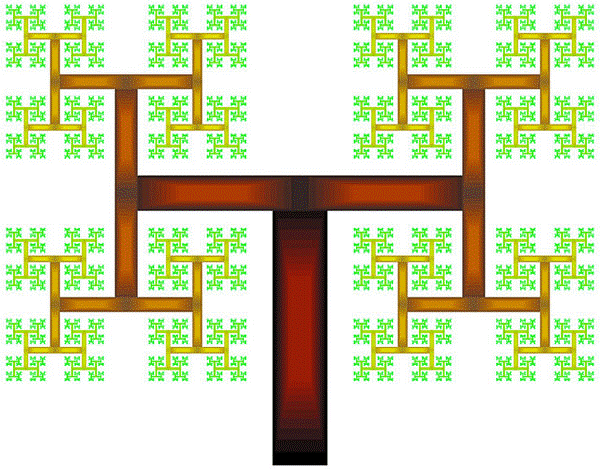
Дерево Пифагора
Называется так потому, что каждая тройка попарно соприкасающихся квадратов ограничивает прямоугольный треугольник и получается картинка, которой часто иллюстрируют теорему Пифагора — «пифагоровы штаны во все стороны равны».
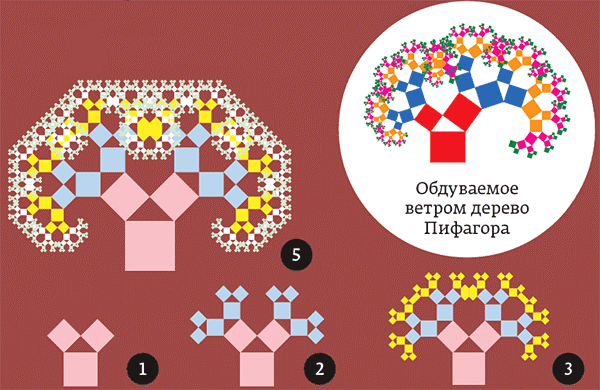
Хорошо видно, что всё дерево ограничено. Если самый большой квадрат единичный, то дерево поместится в прямоугольник 6 × 4. Значит, его площадь не превосходит 24. Но, с другой стороны, каждый раз добавляется в два раза больше троек квадратиков, чем в предыдущий, а их линейные размеры в √2 раз меньше. Поэтому на каждом шаге добавляется одна и та же площадь, которая равна площади начальной конфигурации, то есть 2. Казалось бы, тогда площадь дерева должна быть бесконечна! Но, на самом деле, противоречия здесь нет, потому что довольно быстро квадратики начинают перекрываться и площадь прирастает не так быстро. Она всё-таки конечна, но, по всей видимости, до сих пор точное значение неизвестно, и это открытая проблема.
Если менять углы при основании треугольника, то будут получаться немного другие формы дерева. А при угле 60° все три квадрата окажутся равными, а дерево превратится в периодический узор на плоскости:
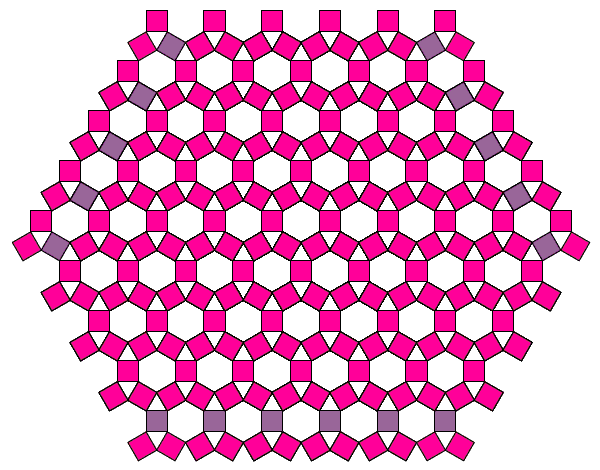
Можно даже заменять квадраты на прямоугольники. Тогда дерево будет больше похоже на настоящие деревья. А при некоторой художественной обработке получаются довольно реалистичные изображения.
Кривая Пеано
Впервые такой объект появился в статье итальянского математика Джузеппе Пеано в 1890 году. Пеано пытался найти хоть сколько-нибудь наглядное объяснение того, что отрезок и квадрат равномощны (если рассматривать их как множества точек), то есть в них «одинаковое» количество точек. Эта теорема была ранее доказана Георгом Кантором в рамках придуманной им теории множеств. Однако подобные противоречащие интуиции результаты вызывали большой скепсис по отношению к новой теории. Пример Пеано — построение непрерывного отображения из отрезка на квадрат — стал хорошим подтверждением правоты Кантора.

Любопытно, что в статье Пеано не было ни одной иллюстрации. Иногда выражение «кривая Пеано» относят не к конкретному примеру, а к любой кривой, которая заполняет часть плоскости или пространства.
Кривая Гильберта
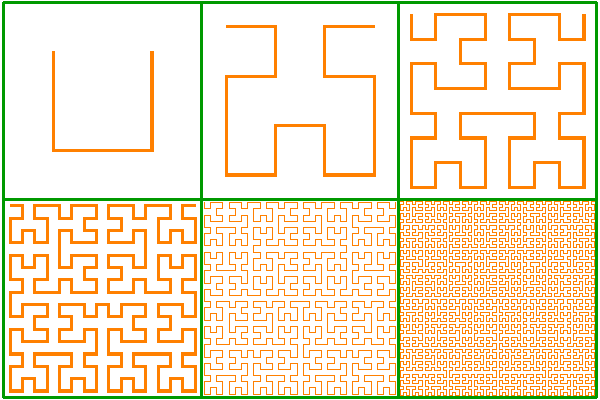
Эта кривая (кривая Гильберта) была описана Давидом Гильбертом в 1891 году. Мы можем увидеть лишь конечные приближения к тому математическому объекту, который имеется в виду — сам он получится в пределе только после бесконечного числа операций.
Фрактал «Греческий крест»
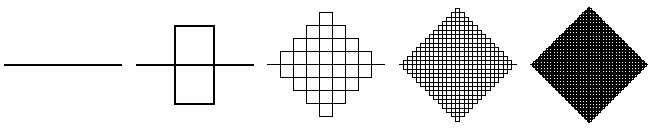
Еще один интересный пример — фрактал «Греческий крест».
Кривая Госпера

Кривая Госпера, или снежинка Госпера – еще одна из вариаций кривых линий.
Кривая Леви
Хотя этот объект изучал еще итальянец Эрнесто Чезаро в 1906 году, его самоподобие и фрактальные свойства исследовал в 1930-х годах француз Поль Пьер Леви. Фрактальная размерность границы этого фрактала примерно равна 1,9340. Но это довольно сложный математический результат, а точное значение неизвестно.

За сходство с буквой «С», написанной витиеватым шрифтом, ее еще называют С-кривой Леви. Если приглядеться, то можно заметить, что кривая Леви похожа на форму кроны дерева Пифагора.
Куб Гильберта
А есть еще и трехмерные аналоги таких линий. Например, трехмерная кривая Гильберта, или куб Гильберта.

Элегантная металлическая версия трехмерной кривой Гильберта (третья итерация), созданная профессором компьютерных наук Калифорнийского университета в Беркли Карло Секином.
Треугольник Серпинского
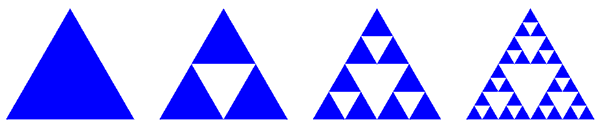
Этот фрактал описал в 1915 году польский математик Вацлав Серпинский. Чтобы его получить, нужно взять равносторонний треугольник с внутренностью, провести в нём средние линии и выкинуть центральный из четырех образовавшихся маленьких треугольников. Дальше эти же действия нужно повторить с каждым из оставшихся трех треугольников, и т.д. На рисунке показаны первые три шага, а на флэш-демонстрации вы можете потренироваться и получить шаги вплоть до десятого.
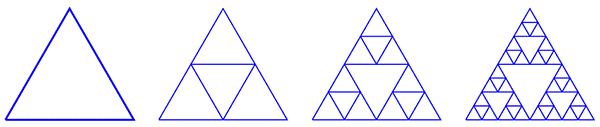
Выкидывание центральных треугольников — не единственный способ получить в итоге треугольник Серпинского. Можно двигаться «в обратном направлении»: взять изначально «пустой» треугольник, затем достроить в нём треугольник, образованный средними линиями, затем в каждом из трех угловых треугольников сделать то же самое, и т.д. Поначалу фигуры будут сильно отличаться, но с ростом номера итерации они будут всё больше походить друг на друга, а в пределе совпадут.
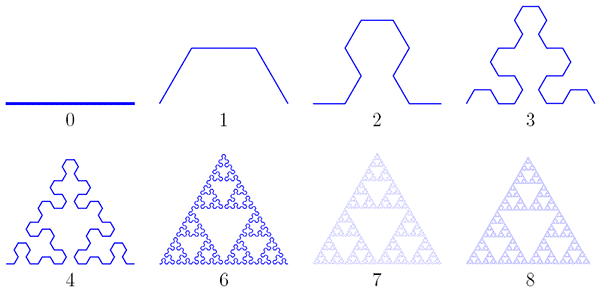
Следующий способ получить треугольник Серпинского еще больше похож на обычную схему построения геометрических фракталов с помощью замены частей очередной итерации на масштабированный фрагмент. Здесь на каждом шаге составляющие ломаную отрезки заменяются на ломаную из трех звеньев (она сама получается в первой итерации). Откладывать эту ломаную нужно попеременно то вправо, то влево. Видно, что уже восьмая итерация очень близка к фракталу, и чем дальше, тем ближе будет подбираться к нему линия.
Ковер (квадрат, салфетка) Серпинского
На треугольниках уважаемый математик не остановился и 1916 году им была описана квадратная версия. Ему удалось доказать, что любая кривая, которую можно нарисовать на плоскости без самопересечений, гомеоморфна какому-то подмножеству этого дырявого квадрата. Как и треугольник, квадрат можно получить из разных конструкций. Справа изображен классический способ: разделение квадрата на 9 частей и выбрасывание центральной части. Затем то же повторяется для оставшихся 8 квадратов, и т.д.

Как и у треугольника, у квадрата нулевая площадь. Фрактальная размерность ковра Серпинского равна log38, вычисляется аналогично размерности треугольника.
Пирамида Серпинского

Один из трехмерных аналогов треугольника Серпинского. Строится аналогично, с учетом трехмерности происходящего: 5 копий начальной пирамиды, сжатой в два раза, составляют первую итерацию, ее 5 копий составят вторую итерацию и так далее. Фрактальная размерность равна log25. У фигуры нулевой объем (на каждом шаге половина объема выбрасывается), но при этом площадь поверхности сохраняется от итерации к итерации, и у фрактала она такая же, как и у начальной пирамиды.
Губка Менгера
Обобщение ковра Серпинского в трехмерное пространство. Чтобы построить губку, нужно бесконечное повторение процедуры: каждый из кубиков, из которых состоит итерация, делится на 27 втрое меньших кубиков, из которых выбрасывают центральный и его 6 соседей. То есть каждый кубик порождает 20 новых, в три раза меньших. Поэтому фрактальная размерность равна log320. Этот фрактал является универсальной кривой: любая кривая в трехмерном пространстве гомеоморфна некоторому подмножеству губки. У губки нулевой объем (так как на каждом шаге он умножается на 20/27), но при этом бесконечно большая площадь.

Геометрических фракталов имеется еще огромное множество, а площадь поверхности этой странички, к сожалению, не бесконечна. Поэтому давайте перейдем к следующему типу фракталов – алгебраическому.
Динамические (алгебраические) фракталы
Фракталы этого типа возникают при исследовании нелинейных динамических систем (отсюда и название). Поведение такой системы можно описать комплексной нелинейной функцией (многочленом) f(z).
Множества Жюлиа
Возьмем какую-нибудь начальную точку z0 на комплексной плоскости. Теперь рассмотрим бесконечную последовательность чисел на комплексной плоскости, каждое следующее из которых получается из предыдущего: z0, z1 = f(z0), z2 = f(z1), … zn+1 = f(zn). В зависимости от начальной точки z0 такая последовательность может вести себя по-разному: стремиться к бесконечности при n → ∞; сходиться к какой-то конечной точке; циклически принимать ряд фиксированных значений; возможны и более сложные варианты.
Таким образом, любая точка z комплексной плоскости имеет свой характер поведения при итерациях функции f(z), а вся плоскость делится на части. При этом точки, лежащие на границах этих частей, обладают таким свойством: при сколь угодно малом смещении характер их поведения резко меняется (такие точки называют точками бифуркации). Так вот, оказывается, что множества точек, имеющих один конкретный тип поведения, а также множества бифуркационных точек часто имеют фрактальные свойства. Это и есть множества Жюлиа для функции f(z).
Множество Мандельброта
Оно строится немного иначе. Рассмотрим функцию fc(z) = z2 + с, где c — комплексное число. Построим последовательность этой функции с z0 = 0, в зависимости от параметра с она может расходиться к бесконечности или оставаться ограниченной. При этом все значения с, при которых эта последовательность ограничена, как раз и образуют множество Мандельброта. Оно было детально изучено самим Мандельбротом и другими математиками, которые открыли немало интересных свойств этого множества.
Видно, что определения множеств Жюлиа и Мандельброта похожи друг на друга. На самом деле эти два множества тесно связаны. А именно, множество Мандельброта — это все значения комплексного параметра c, при которых множество Жюлиа fc(z) связно (множество называется связным, если его нельзя разбить на две непересекающиеся части, с некоторыми дополнительными условиями).
Фрактал Галлея
Такие фракталы получаются, если в качестве правила для построения динамического фрактала использовать формулу Галлея для поиска приближенных значений корней функции. Формула довольно громоздкая, так что кто хочет, может посмотреть ее в Википедии. Идея метода почти та же, что используется для рисования динамических фракталов: берем какое-нибудь начальное значение (как обычно, здесь речь идет о комплексных значениях переменных и функций) и применяем к нему много раз формулу, получая последовательность чисел. Почти всегда она сходится к одному из нулей функции (то есть значению переменной, при котором функция принимает значение 0). Метод Галлея, несмотря на громоздкость формулы, работает эффективнее метода Ньютона: последовательность сходится к нулю функции быстрее.
Фрактал Ньютона
Еще один тип динамических фракталов составляют фракталы (так называемые бассейны) Ньютона. Формулы для их построения основаны на методе решения нелинейных уравнений, который был придуман великим математиком еще в XVII веке. Применяя общую формулу метода Ньютона zn+1 = zn – f(zn)/f'(zn), n = 0, 1, 2, … для решения уравнения f(z) = 0 к многочлену zk – a, получим последовательность точек: zn+1 = ((k – 1)znk – a)/kznk–1, n = 0, 1, 2, … . Выбирая в качестве начальных приближений различные комплексные числа z0, будем получать последовательности, которые сходятся к корням этого многочлена. Поскольку корней у него ровно k, то вся плоскость разбивается на k частей — областей притяжения корней. Границы этих частей имеют фрактальную структуру (заметим в скобках, что если в последней формуле подставить k = 2, а в качестве начального приближения взять z0 = a, то получится формула, которую реально используют для вычисления квадратного корня из a в компьютерах). Наш фрактал получается из многочлена f(z) = z3 – 1.
Применение фракталов в промышленности и быту
Ученые – очень увлеченные личности. Их хлебом не корми, дай пофантазировать на абстрактные темы. Но мы с вами люди практичные, и, прочитав все то, что написано выше, у многих уже наверняка возник резонный вопрос: «ну и че?». Так вот, что же все-таки привнесло это знание в мир?
Во-первых, фракталы используются в компьютерных системах, причем очень плотно. Наиболее полезным использованием фракталов в компьютерной науке является фрактальное сжатие данных. В основе этого вида сжатия лежит тот факт, что реальный мир хорошо описывается фрактальной геометрией. При этом картинки сжимаются гораздо лучше, чем это делается обычными методами (такими как jpeg или gif). Другое преимущество фрактального сжатия в том, что при увеличении картинки не наблюдается эффекта пикселизации (увеличения размеров точек до размеров, искажающих изображение). При фрактальном же сжатии, после увеличения, картинка часто выглядит даже лучше, чем до него.
Во-вторых, это механика жидкостей и, как следствие, нефтяная промышленность. Дело в том, что изучение турбулентности в потоках очень хорошо подстраивается под фракталы. Турбулентные потоки хаотичны и поэтому их сложно точно смоделировать. И здесь помогает переход к их фрактальному представлению, что сильно облегчает работу инженерам и физикам, позволяя им лучше понять динамику сложных потоков. При помощи фракталов также можно смоделировать языки пламени. Пористые материалы хорошо представляются во фрактальной форме в связи с тем, что они имеют очень сложную геометрию. Это используется в нефтяной науке.
В-третьих, приходя вечером с завода домой, ложась на любимый боевой диван, вы включаете телевизор, который тоже имеет отношение к фракталам. Дело в том, что для передачи данных на расстояния используются антенны, имеющие фрактальные формы, что сильно уменьшает их размеры и вес.
Использование фрактальной геометрии при проектировании антенных устройств было впервые применено американским инженером Натаном Коэном, который жил тогда в центре Бостона, где была запрещена установка на зданиях внешних антенн. Коэн вырезал из алюминиевой фольги фигуру в форме кривой Коха и затем наклеил ее на лист бумаги, а затем присоединил к приемнику. Оказалось, что такая антенна работает не хуже обычной. И хотя физические принципы такой антенны не изучены до сих пор, это не помешало Коэну обосновать собственную компанию и наладить их серийный выпуск. В данный момент американская фирма Fractal Antenna System разработала антенну нового типа. Теперь можно отказаться от использования в мобильных телефонах торчащих наружных антенн — так называемая фрактальная антенна располагается прямо на основной плате внутри аппарата.
Кроме того, фракталы используются для описания кривизны поверхностей. Неровная поверхность характеризуется комбинацией из двух разных фракталов. Еще они используются в разработке биосенсорных взаимодействий, исследованиях биения сердца, моделировании хаотических процессов, в частности при описании моделей популяций животных и так далее.
Фрактальная структура рынка
Вся эта ода фракталам была бы напрасной, если бы не фрактальная природа финансовых рынков. Да, наконец мы дошли до обсуждения того самого вопроса, ради которого я эту статью и писал.
Итак, в настоящее время применяется много способов анализа финансовых рынков, на основе которых трейдеры создают свои торговые стратегии. Среди различных инструментов анализа и прогноза фрактальный анализ стоит немного в стороне. Это отдельная разносторонняя и интересная теория для обсуждения и изучения. Первое впечатление говорит о простоте тематики, однако копни глубже, и будет видно много скрытых нюансов.
Понимание фракталов — это ключ к видению скрытой информации о рынке. А ведь именно она является одним из ключевых факторов рыночного успеха спекулянта и залогом большой стабильной прибыли.
14 октября 2010 года ушел из жизни Бенуа Мандельброт — человек, во многом изменивший наше представление об окружающих нас предметах и обогативший наш язык словом «фрактал».

Как вы уже знаете, именно благодаря Мандельброту мы знаем, что фракталы окружают нас повсюду. Некоторые из них непрерывно меняются, как движущиеся облака или пламя, в то время как другие, подобно береговым линиям, деревьям или нашим сосудистым системам — сохраняют структуру, приобретенную в процессе эволюции. При этом реальный диапазон масштабов, где наблюдаются фракталы, простирается от расстояний между молекулами в полимерах до расстояния между скоплениями галактик во Вселенной. Богатейшая коллекция таких объектов собрана в знаменитой книге Мандельброта «Фрактальная геометрия природы».
Важнейшим классом природных фракталов являются хаотические временные ряды, или упорядоченные во времени наблюдения характеристик различных природных, социальных и технологических процессов. Среди них имеются как традиционные (геофизические, экономические, медицинские), так и те, которые стали известными относительно недавно (ежедневные колебания уровня преступности или ДТП в регионе, изменения количества показов определенных сайтов в интернете и т.д.). Эти ряды, обычно, порождаются сложными нелинейными системами, которые имеют самую различную природу. Однако у всех характер поведения повторяется на разных масштабах. Наиболее популярными их представителями являются финансовые временные ряды (в первую очередь цены акций и курсы валют).
Самоподобная структура таких рядов известна очень давно. В одной из своих статей Мандельброт писал, что его интерес к котировкам на фондовом рынке начался с высказывания одного из биржевиков: «…Движения цен большинства финансовых инструментов внешне похожи на разных масштабах времени и цены. По внешнему виду графика наблюдатель не может сказать, относятся данные к недельным, дневным или же часовым изменениям».
Мандельброт, занимающий совершенно особое место в финансовой науке, имел славу «ниспровергателя основ», вызывая среди экономистов явно неоднозначное к себе отношение. С момента возникновения современной финансовой теории, основанной на концепции общего равновесия, он был одним из главных ее критиков и до конца жизни пытался найти ей приемлемую альтернативу. Однако именно Мандельброт разработал систему понятий, которая при соответствующей модификации, как оказалось, позволяет не только построить эффективный прогноз, но и предложить, видимо, единственное на данный момент эмпирическое обоснование классической теории финансов.
Основной характеристикой фрактальных структур является фрактальная размерность D, введенная Феликсом Хаусдорфом в 1919 году. Для временных рядов чаще используют индекс Херста H, который связан с фрактальной размерностью соотношением D = 2 – H и является показателем персистентности (способности сохранять определенную тенденцию) временного ряда.
Обычно различают три принципиально разных режима, которые могут существовать на рынке: при Н = 0,5 поведение цен описывается моделью случайного блуждания; при Н > 0,5 цены находятся в состоянии тренда (направленного движения вверх или вниз); при H < 0,5 цены находятся в состоянии флэта, или частых колебаний в достаточно узком диапазоне цен. Однако для надежного вычисления H (так же как и D) требуется слишком много данных, что исключает возможность использования этих характеристик в качестве показателей, определяющих локальную динамику временного ряда.
Как известно, базовой моделью финансовых временных рядов является модель случайного блуждания, впервые полученная Луисом Башелье для описания наблюдений за ценами акций на Парижской фондовой бирже. В результате переосмысления этой модели, которая иногда наблюдается в поведении цен, возникла концепция эффективного рынка, на котором цена в полной мере отражает всю доступную информацию.
Для существования такого рынка достаточно предположить, что на нем действует большое число полностью информированных рациональных агентов, которые мгновенно реагируют на поступающую информацию и корректируют цены, приводя их в состояние равновесия. Все основные результаты классической теории финансов (портфельная теория, модель CAPM, модель Блэка—Шоулза и другие) были получены в рамках именно такого подхода. В настоящее время концепция эффективного рынка продолжает играть доминирующую роль и в финансовой теории, и в финансовом бизнесе.
Тем не менее, к началу 60-х годов прошлого века эмпирические исследования показали, что сильные изменения цен на рынке происходят значительно чаще, чем предсказывала основная модель эффективного рынка (модель случайного блуждания). Одним из первых, кто подверг концепцию эффективного рынка всесторонней критике, был как раз Мандельброт.
Действительно, если корректно вычислить значение показателя H для какой-либо акции, то оно, вероятнее всего, будет отлично от H = 0,5, которое соответствует модели случайного блуждания. Мандельброт нашел все возможные обобщения этой модели, которые могут иметь отношение к реальному поведению цен. Как оказалось, это, с одной стороны, процессы, названные им полетом Леви, а с другой — процессы, которые он назвал обобщенным броуновским движением.
Для описания поведения цен обычно используют концепцию фрактального рынка, которую принято рассматривать в качестве альтернативы эффективному рынку. Концепция предполагает, что на рынке есть широкий спектр агентов с разными инвестиционными горизонтами и, следовательно, разными предпочтениями. Эти горизонты меняются от нескольких минут для внутридневных трейдеров до нескольких лет для крупных банков и инвестиционных фондов.
Устойчивым положением на таком рынке является режим, при котором «средняя доходность не зависит от масштаба, если не считать умножения на соответствующий масштабный коэффициент». Фактически речь идет о целом классе режимов, каждый из которых определяется своим значением показателя H. При этом значение H = 0,5 оказывается одним из многих возможных и, следовательно, равноправным с любым другим значением. Эти и другие близкие соображения стали поводом для серьезных сомнений относительно существования действительного равновесия на фондовом рынке.
Посмотрите на ценовые графики снизу:
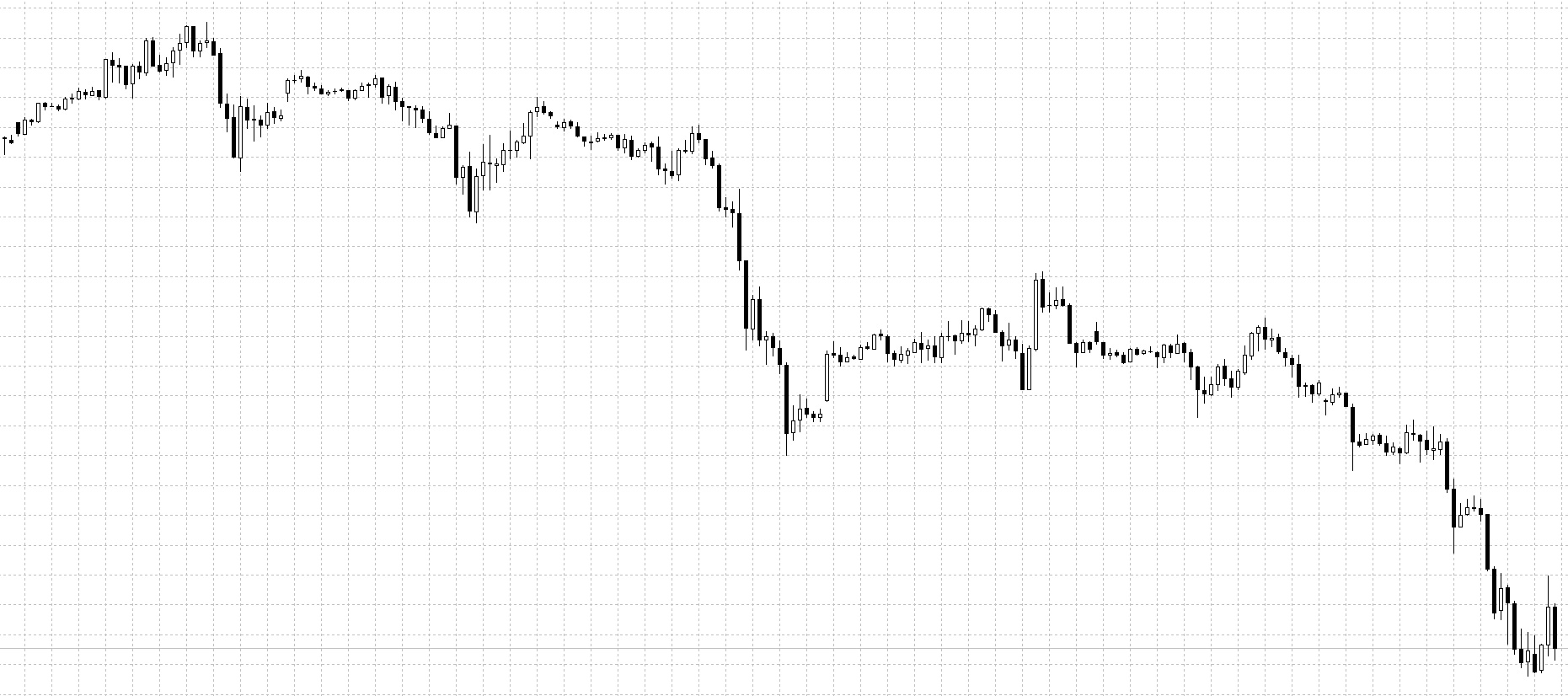
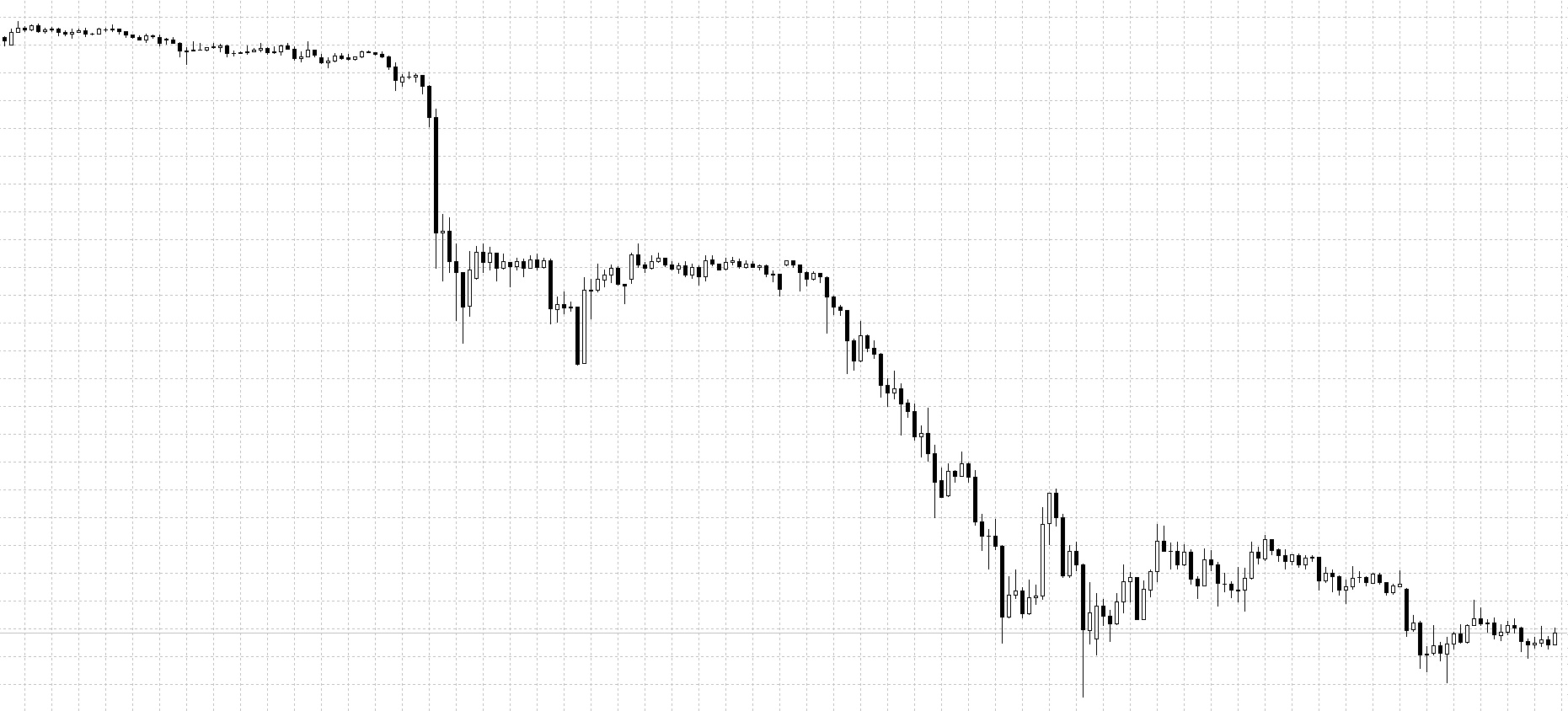
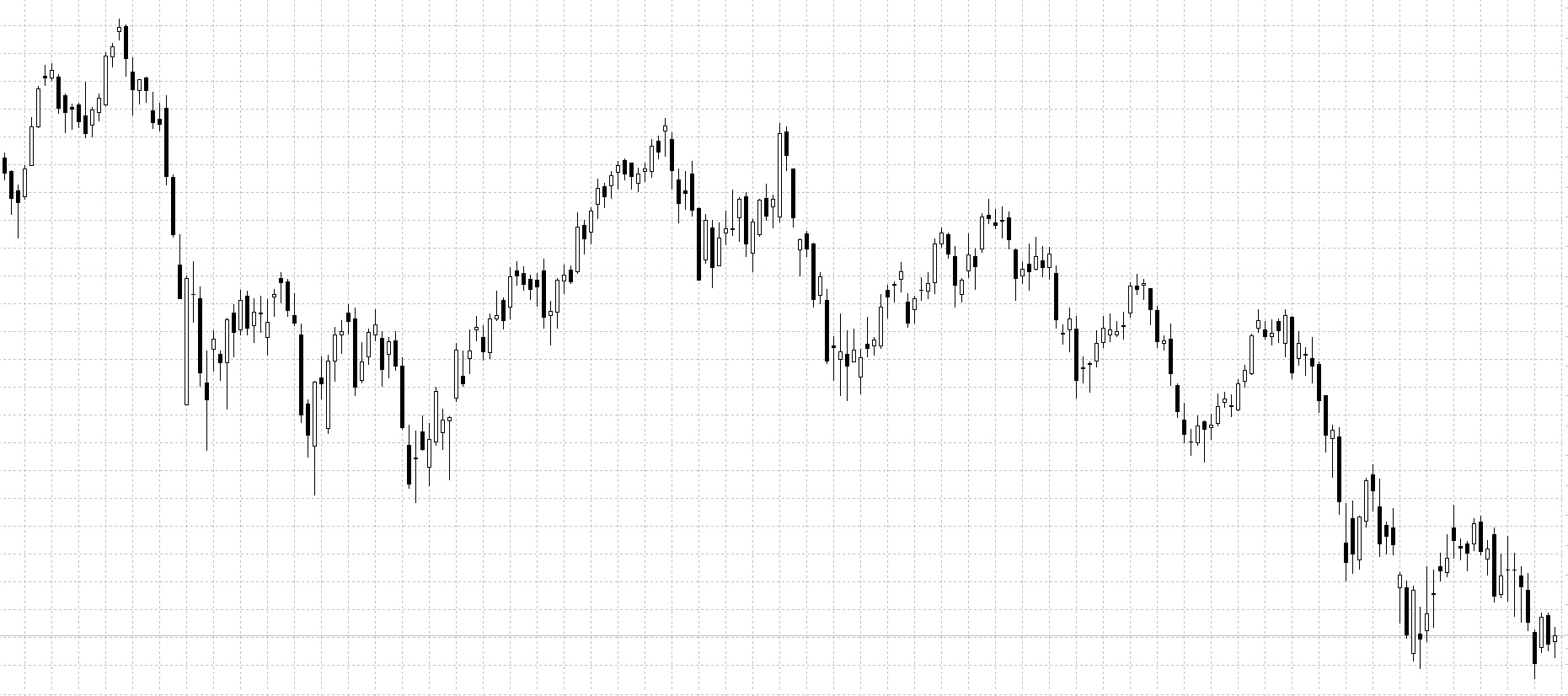
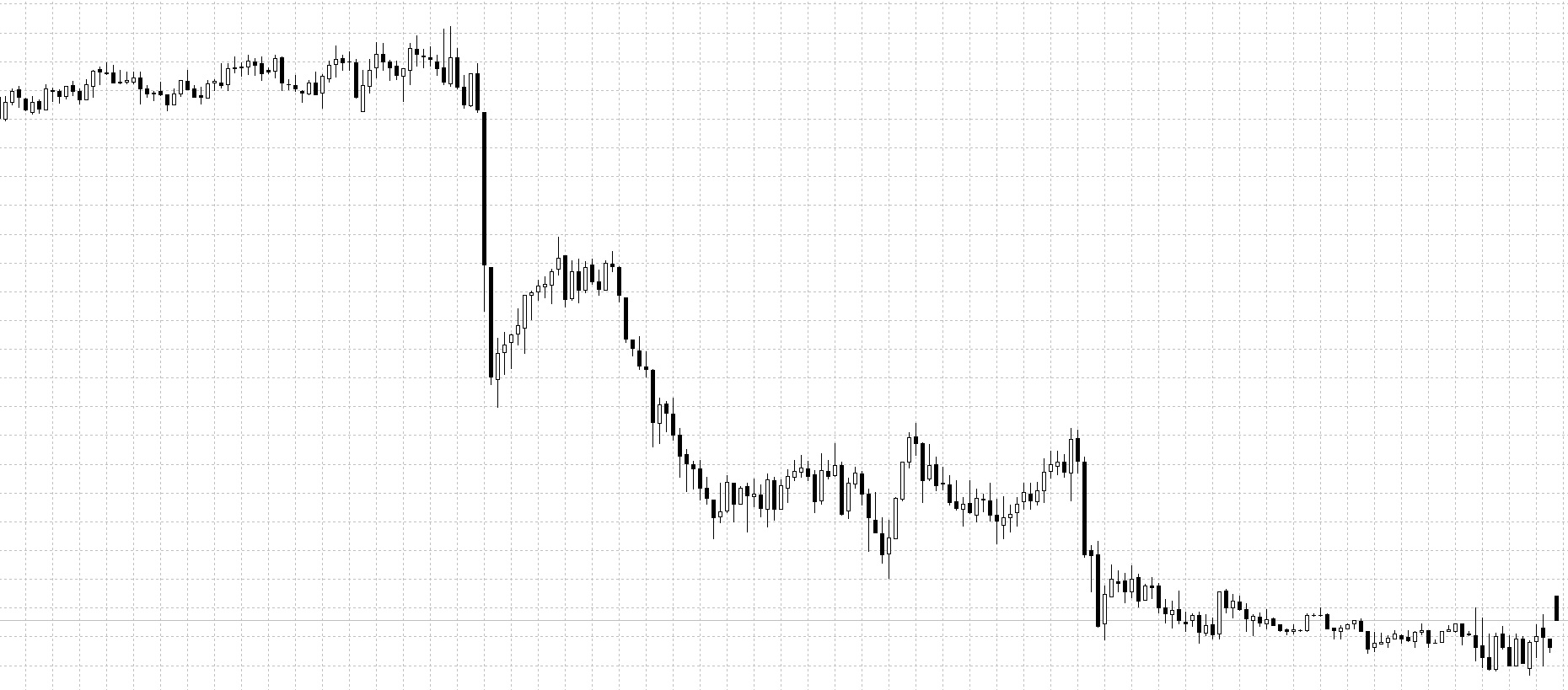
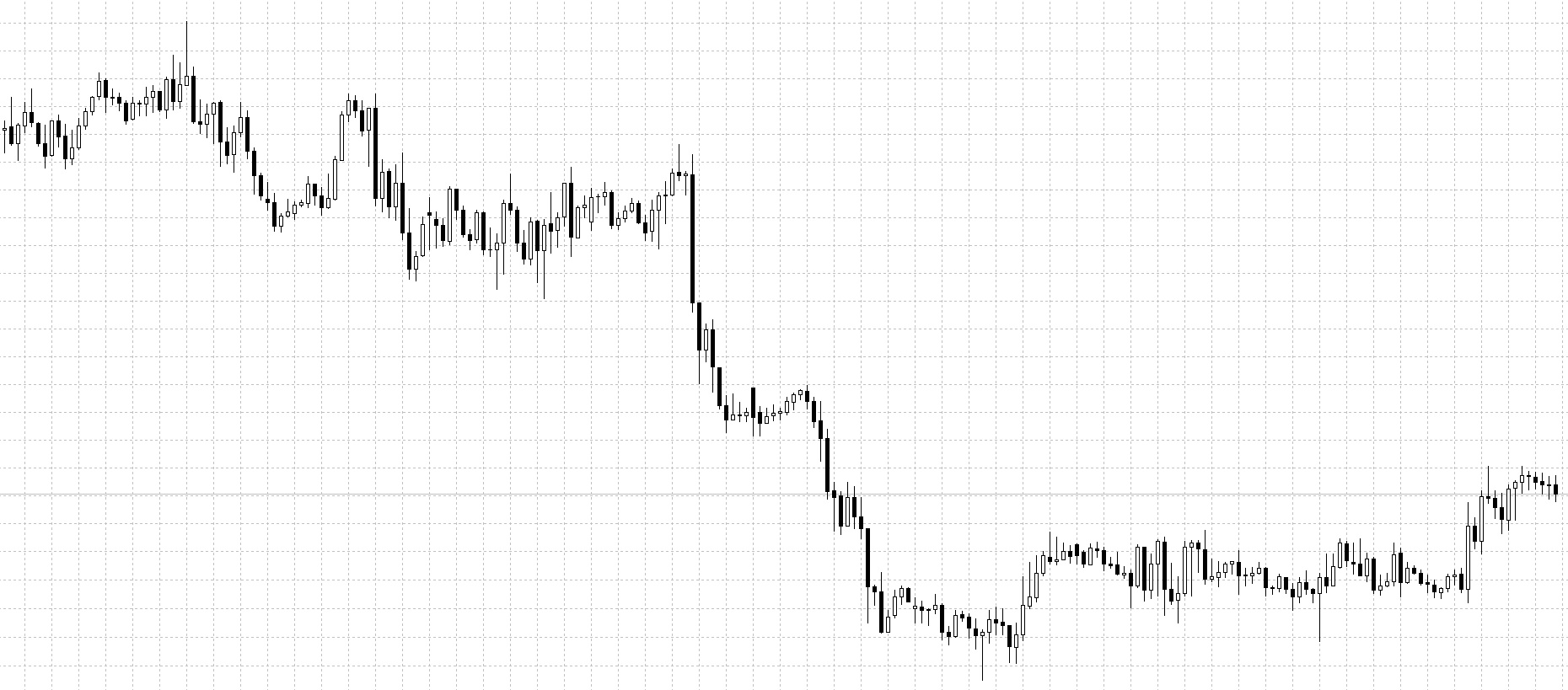
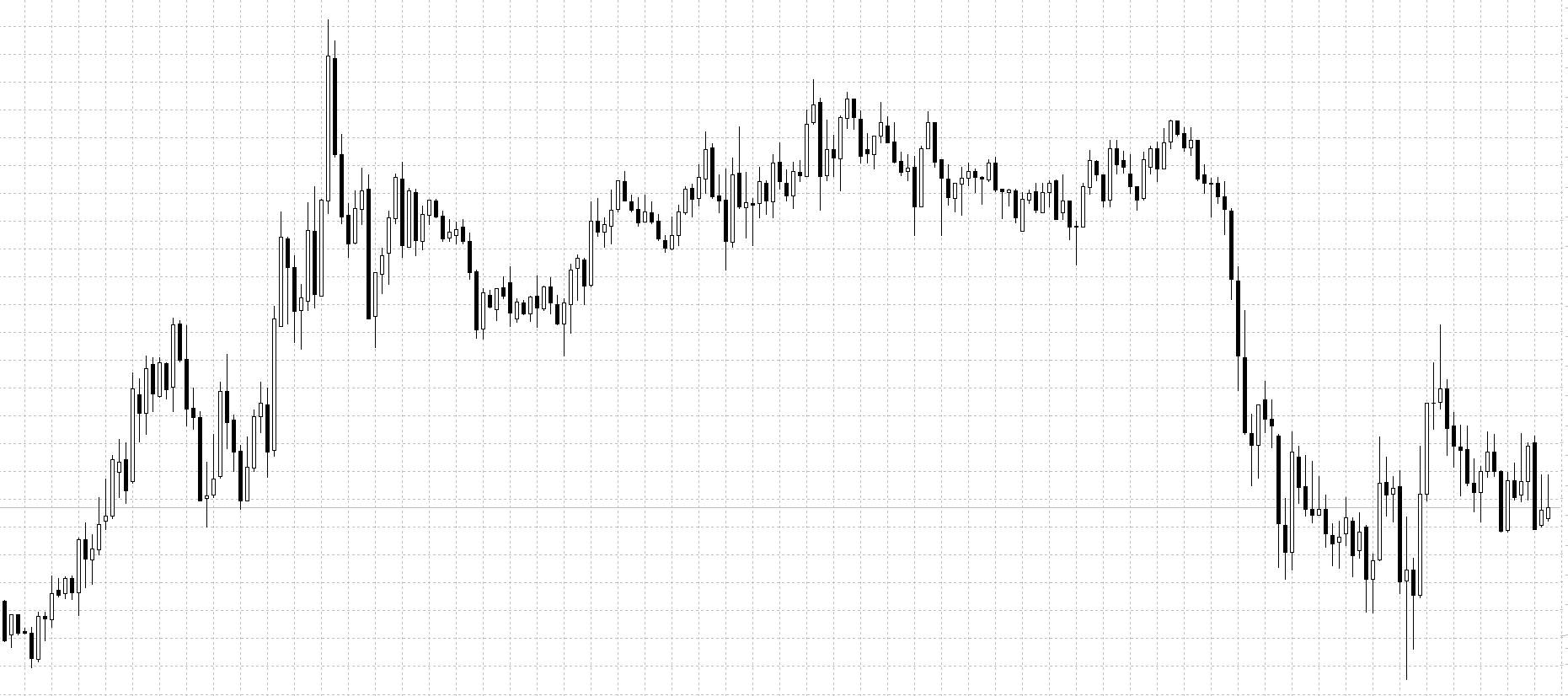
Видно, что цена совершает постоянные колебания, образовывая при этом структуру повторяющегося характера. Просматривается она на всех рынках, независимо от временного масштаба.
На изображении представлены графики: BRN M30, BTCUSD H1, DAX30 D1, EURSGD M5, USDCHF H1, XAUUSD M15. Без подписей и разъяснений вряд ли кто-нибудь сможет отличить их друг от друга.
Этих графики не совсем похожи друг на друга, но имеют некоторые общие модели. На заданном промежутке времени цена движется в одном направлении, затем меняет свое направление на обратное и частично восстанавливает предыдущее движение, после вновь разворачивается. Не имеет значения, какой таймфрейм используется для графиков — все они выглядят примерно одинаково (постоянные колебания), так же, как и фракталы.
Колебания образуют волны рынка. Что такое волна? Это импульс и коррекция к нему (движение-разворот-движение в обратном направлении, частично восстанавливающее предыдущее). Такие движения образуют волны.
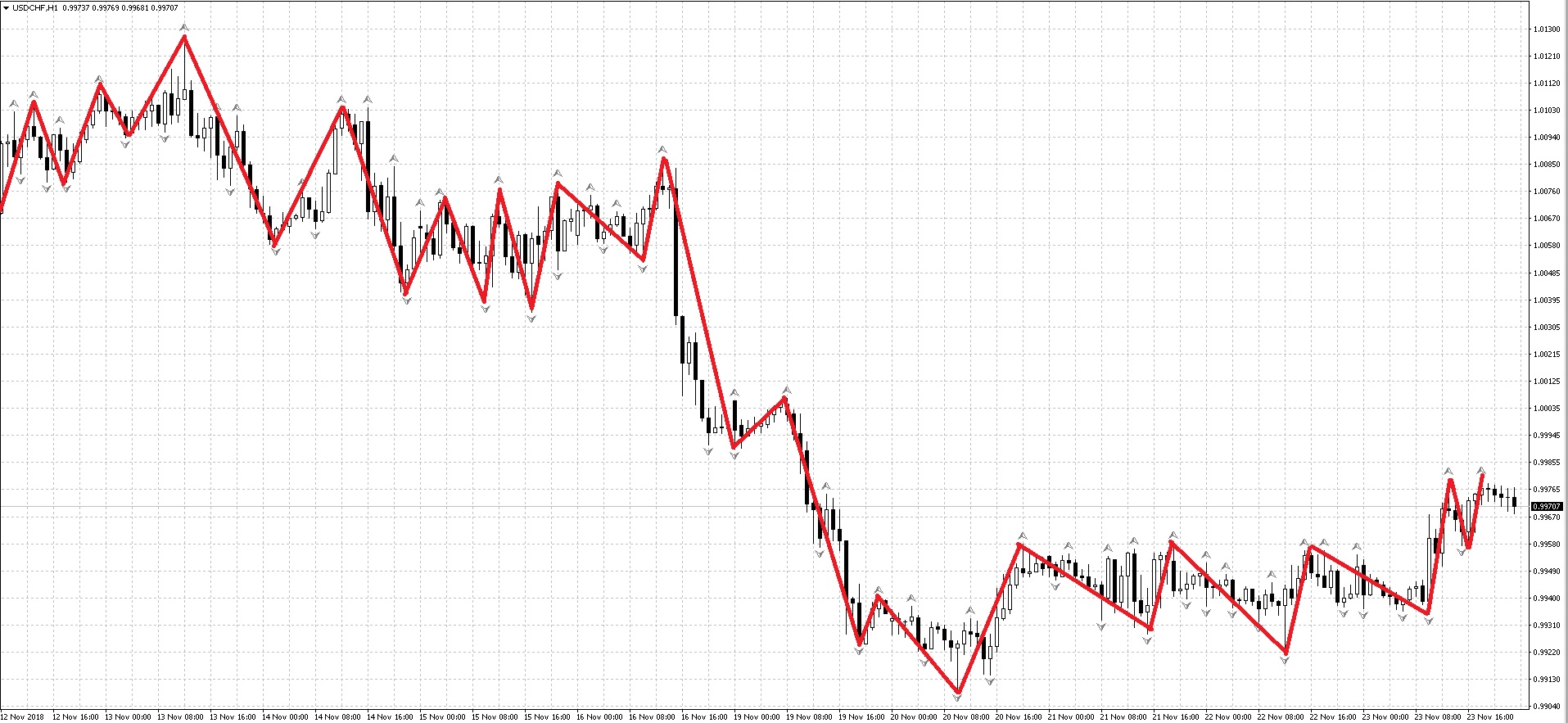
На изображении показаны эти движения, которые образуют волны. Несколько таких волн образуют большую волну аналогичной формы (импульс-коррекция). Несколько малых волн образуют одну волну среднего размера.
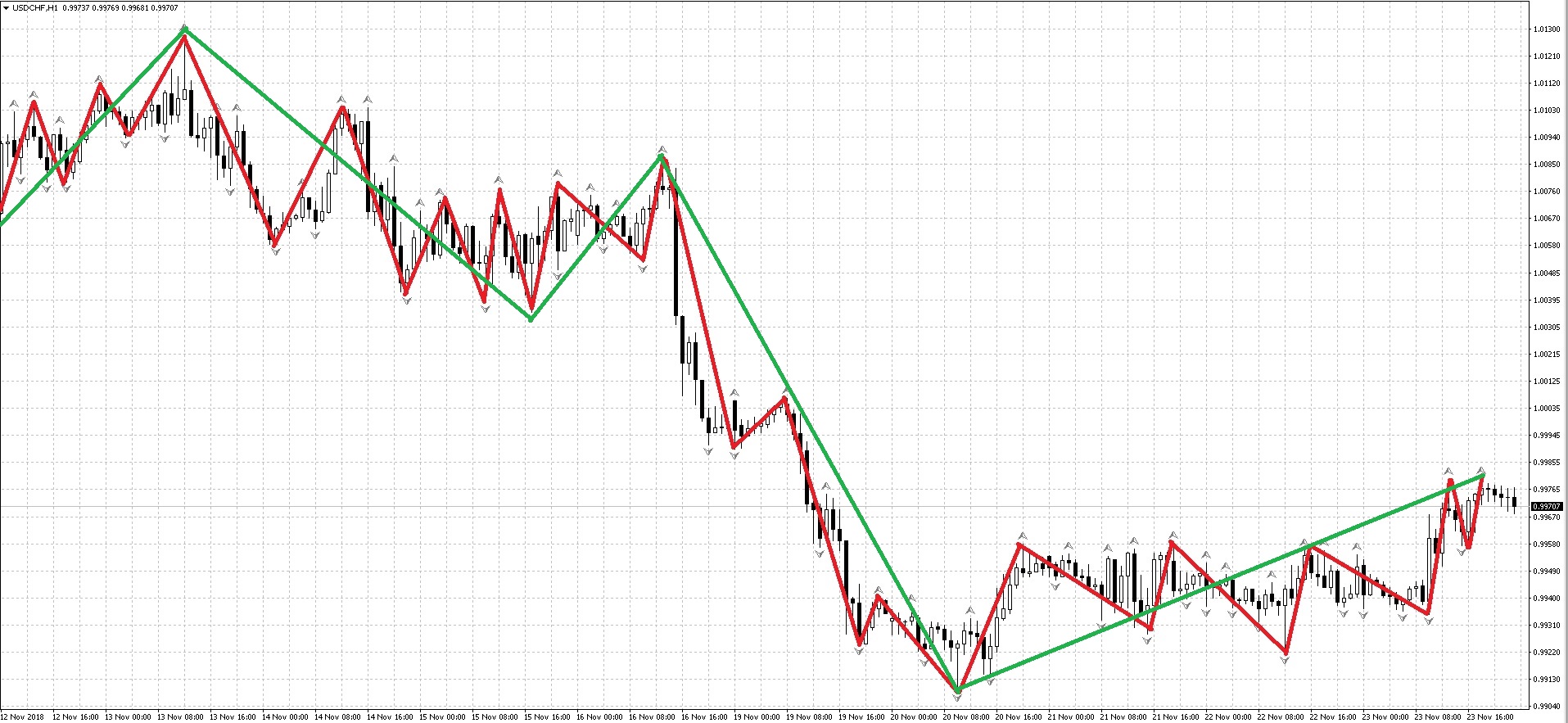
Волны среднего размера образуют одну большую волну. Это и есть суть фрактальной теории на финансовых рынках.
Серии подобных волн образуют направленные движения на рынке – тренды. Подобные тренды, в свою очередь, образуют направленные движения старшего временного порядка. Как и в случае с волнами — небольшие движения образуют одно среднее и т.д. Так различают краткосрочные тренды, среднесрочные и долгосрочные. Это – классическое понимание фрактальной природы рынка.
Фракталы Билла Вильямса
Как я уже говорил, фракталы рынка являются одним из индикаторов в торговой системе Била Вильямса. Считается, что именно он впервые и ввел это название в трейдинг, но, как вы понимаете, это не так. При торговле по фракталам, в сочетании со своим индикатором Аллигатор, автор обнаруживал локальные максимумы или минимумы рынка. Он также писал, что определение фрактальной структуры рынка позволяет найти способ понимания поведения цены.

Вообще же теория фракталов Вильямса в свое время вызвала бурные споры, прежде всего потому, что автор, как считают многие, вставил в свою теорию много научной терминологии (фрактал, аттрактор и так далее) и сделал это не совсем корректно.
Вообще же, фракталы Вильямса появляются на рынке достаточно часто и практически на всех таймфреймах и являются, по сути, простыми локальными экстремумами на отрезке из 5 баров и практически не соответствуют математической теории фракталов. Точно таким же образованием на графике являются и ТД-точки второго порядка Томаса Демарка. Однако, несмотря все эти совпадения — эта теория весьма популярна и до сих пор.
Технический анализ по Вильямсу рассматривает 4 существующих формации фрактала:
истинный фрактал на покупку;
ложный фрактал на покупку;
истинный фрактал на продажу;
ложный фрактал на продажу.
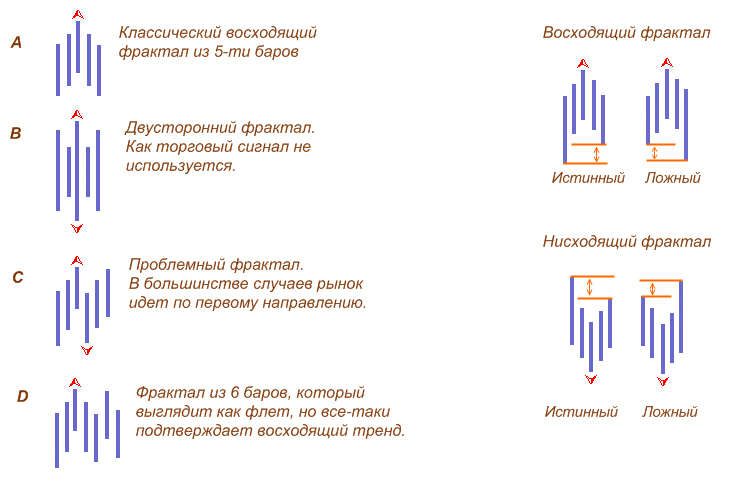
Об истинных и ложных фракталах и о том, как их различать, мы еще поговорим ниже.
Индикатор Fractals в торговом терминале MetaTrader
Индикаторы Билла Вильямса не требуют установки и входят в стандартный набор индикаторов, доступных трейдеру «из коробки». Для того, чтобы прикрепить индикатор фрактал в терминале MetaTrader 4 к графику необходимо: в главном меню (или в окне «Навигатор») выбрать пункт меню «Вставка» — «Индикаторы» — «Билла Вильямса» — «Fractals»:
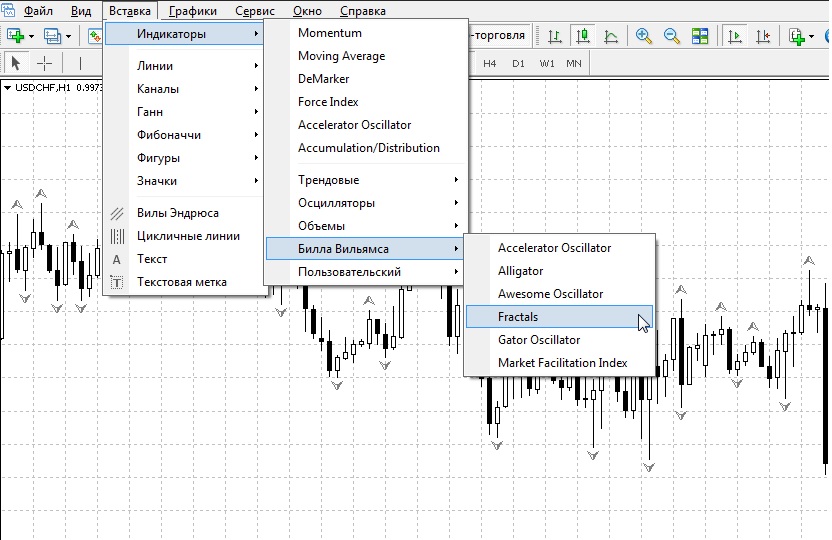
Стандартный индикатор для МТ4 не имеет никаких настроек, кроме цветовых. Его использование с фиксированным периодом «5» сводит на нет все возможности и преимущества данного инструмента. Но для платформы MetaTrader существует множество пользовательских индикаторов, которые помогут решить эту проблему.
Наш форумчанин Pavel888 как раз собрал большую коллекцию из различных индикаторов Fractals в ветке на форуме, за что ему большое спасибо.
Проблема ложности и истинности фракталов
Во время торговли с использованием фракталов существует один важный нюанс – это появление на графике большого количества сигналов, часть из которых являются ложными. Для их фильтрации Билл Вильямс разработал еще один индикатор под названием «Аллигатор», который также можно найти в стандартном наборе индикаторов в MT4.
Проблема ложных фракталов является основным источником ошибок, аналогично оценкам истинности пробоя поддержки/сопротивления. Независимо от конкретной методики общий принцип определения надежности следующий – любые отклонения от классического вида должны вызвать сомнения. Как и во всем теханализе уменьшение таймфрейма приводит к увеличению ложных сигналов и загромождению графика. Примеры неустойчивых фракталов приведены на рисунке ниже.
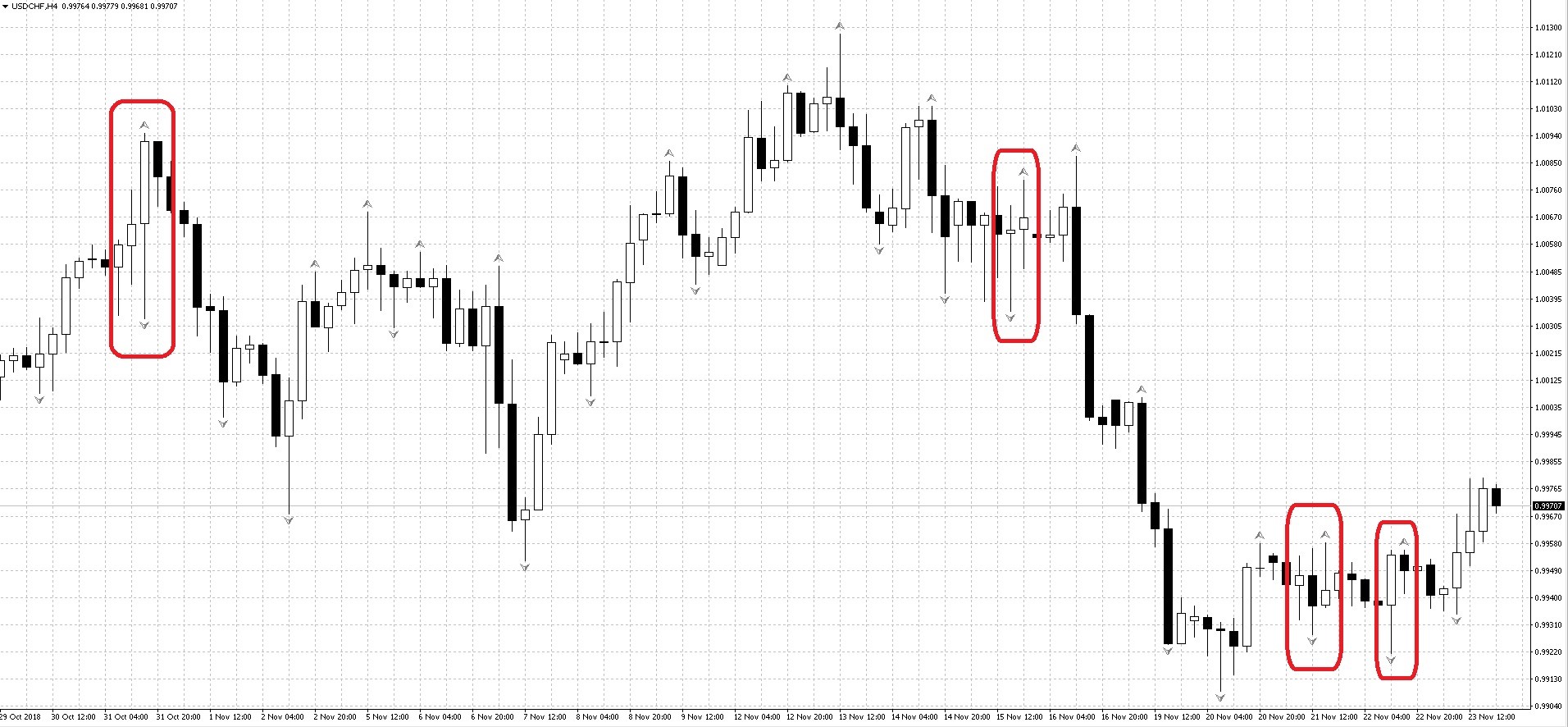
Отрабатывая крупные паттерны, лучше открывать позиции в моменты коррекции последнего ценового импульса, которые находятся в левой части формации. Внутри паттерна надежно работают стандартные Фибоначчи-коррекции на 38% (0,382), 50% (0,500) и 62% (0,618). Если «растягивать» уровни через соседние сигналы индикатора, то можно открываться через лимитные ордера около ключевых уровней.
Таким же образом можно защитить сделку от непредсказуемого обратного пробоя, постепенно перемещая stoploss, для контроля противоположного максимума или минимума последней и предпоследней свечи. Когда структура только формируется, стоп должен быть минимум на 5-10 пунктов выше или ниже последнего сигнала, который дал индикатор Фрактал. Тогда при незначительных откатах мы остаемся в рынке, а если будет полная смена тренда, сделка закроется с минимальным убытком.
Есть еще один способ определить, что перед нами ложные фракталы – когда они пробиты баром с длинной тенью и малым телом (пин-бар). Чем длиннее его «нос», тем сильнее разворотный сигнал, означающий, что рынку не удалось с первого раза перейти уровень последнего паттерна. Если пробой состоялся и следующая свеча закрыта выше High (для продажи) или ниже Low (для покупки) носа, то с большой вероятностью можно пропустить сигнал и подождать следующего. Подобная ситуация может произойти и через 3-5 баров, но обращаем внимание только на бар, пробивший индикатор Fractals.
Практическое использование фракталов
Билл Вильямс советовал использовать фракталы в стратегиях, которые базируются на пробое важных ценовых уровней. Движение цены выше или ниже хотя бы на один пункт от уровня предыдущего фрактала, по мнению автора этого индикатора, уже говорит о пробитии этого уровня ценой.
Пробитие уровня предыдущего фрактала называется прорывом покупателей в случае, если цена поднимается выше предыдущего фрактала, направленного вверх. В обратном случае, когда цена опускается ниже предыдущего фрактала, направленного вниз, говорят о прорыве продавцов. Билл Вильямс советовал расценивать прорыв покупателей или продавцов как сигнал к открытию позиции.
Обычно, трейдеры выставляют отложенные Stop ордера на несколько пунктов выше или ниже фрактала для открытия позиции в случае пробития этого уровня. В таких случаях стоп-лосс, обычно, выставляется на уровне предпоследнего противоположного фрактала.
В классической интерпретации Билл Вильямс советует фильтровать торговые сигналы, подаваемые фракталами, с помощью индикатора «Аллигатор». Так, для открытия позиции на покупку, необходимо, чтобы был пробит фрактал, находящийся выше красной линии (так называемые «Зубы аллигатора»). Автор стратегии советовал входить в рынок сразу после пробития фрактала вверх или же с помощью отложенного ордера BuyStop. Вход в рынок на продажу происходит в случае пробития фрактала, находящегося ниже красной линии.
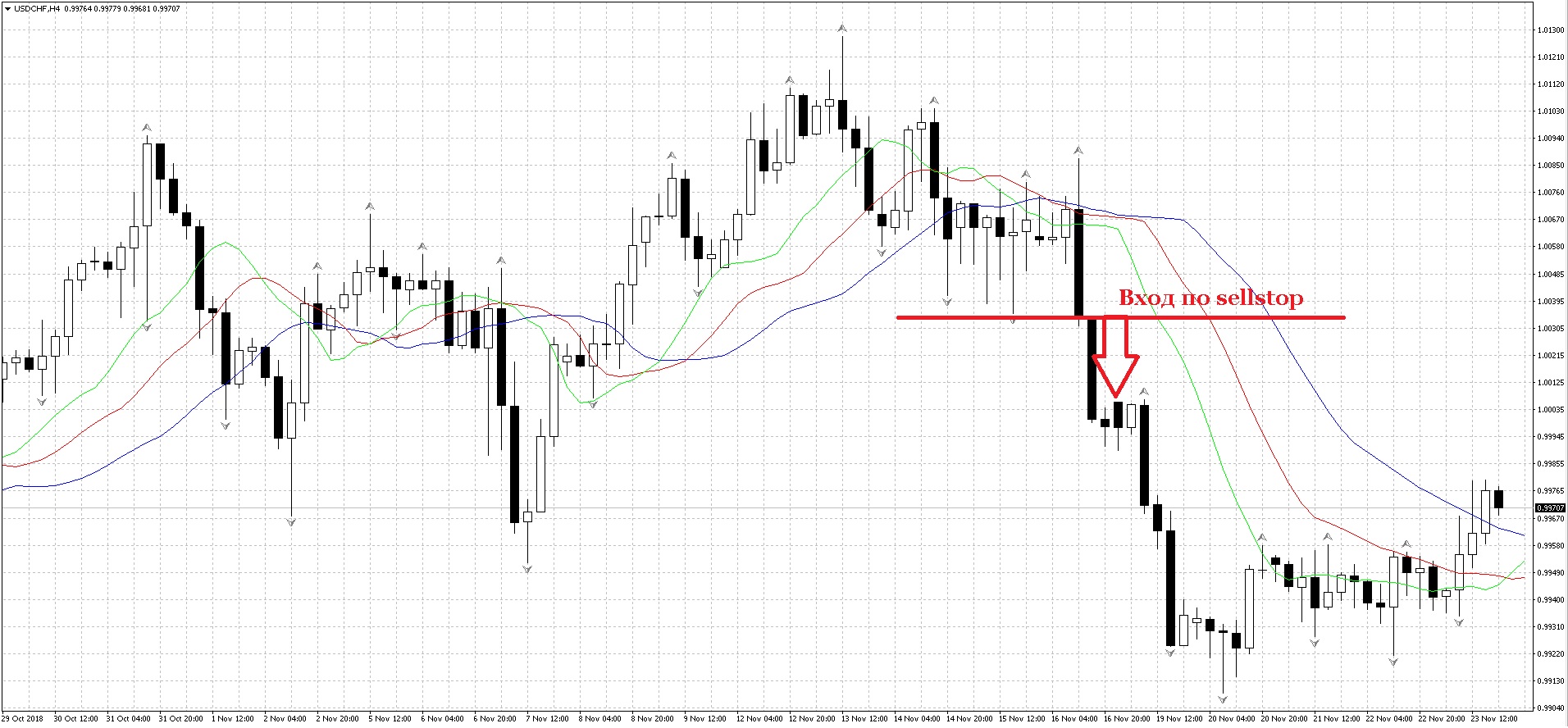
Более подробно с этой стратегией вы можете ознакомиться в статье про систему Билла Вильямса Profitunity. А мы разберем основные практические способы использования фракталов в отрыве от этой ТС.
Торговля на пробой фрактала
Этот метод классический, предложенный Биллом Вильямсом. Как видно из названия, торговля носит пробойных характер и рассчитана на продолжение текущего тренда. Вход в сделку осуществляется отложенным стоп-ордером на пробой ближайшего к цене фрактала. Пример вы можете видеть на рисунке выше.
Как пишет сам автор, данная методика торговли будет давать много ложных входов, поэтому Билл предлагает фильтровать сигналы с помощью индикатора «Аллигатор». В принципе, индикатор «Аллигатор» можно заменить обычными средними скользящими и также использовать их как фильтр. Но повторюсь, что рассматривать фракталы и «Аллигатор» в отрыве от других инструментов Вильямса не имеет смысла, поэтому мы не будем останавливаться на этом и двинемся дальше.
Фракталы как уровни поддержки/сопротивления
Если Вы хотя бы раз сталкивались с уровнями поддержки/сопротивления, то знаете, насколько сложно их строить, особенно, если вы новичок. И сложность вся эта возникает из-за субъективности этого инструмента. Когда мы строим уровни, то не можем с уверенностью сказать, правильно ли мы построили их или нет. Билл Вильямс со своими фракталами дает нам прекрасный инструмент для поиска и построения значимых уровней поддержки и сопротивления.
Давайте накинем индикатор на какой-нибудь график и проанализируем с точки зрения уровней.
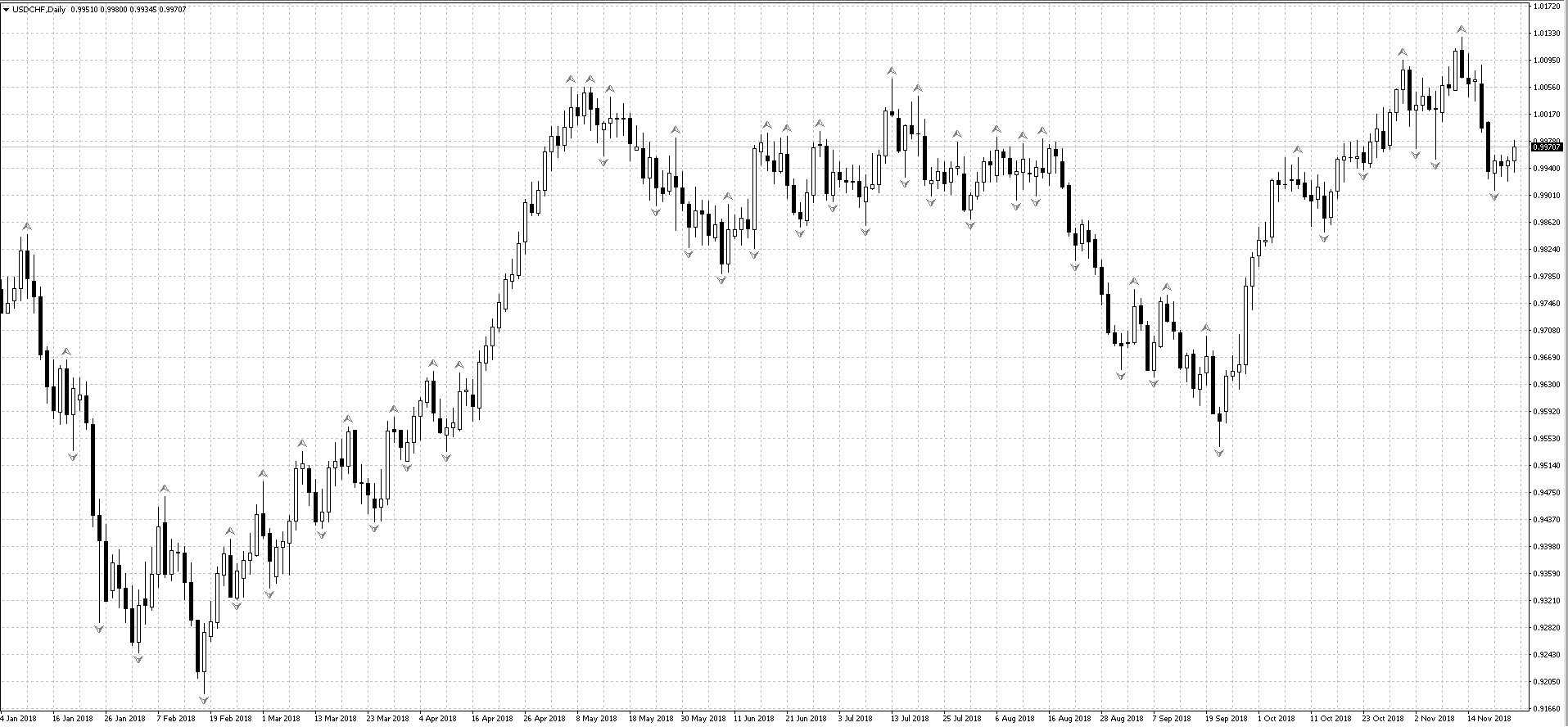
Это график USDCHF D1 с классическим фракталом. Да, график просто пестрит от этих стрелочек. Если через каждый экстремум, выделенный индикатором, провести горизонтальную линию, то за этими линиями станет не видно самого графика.
Давайте увеличим число периодов и посмотрим на результат:
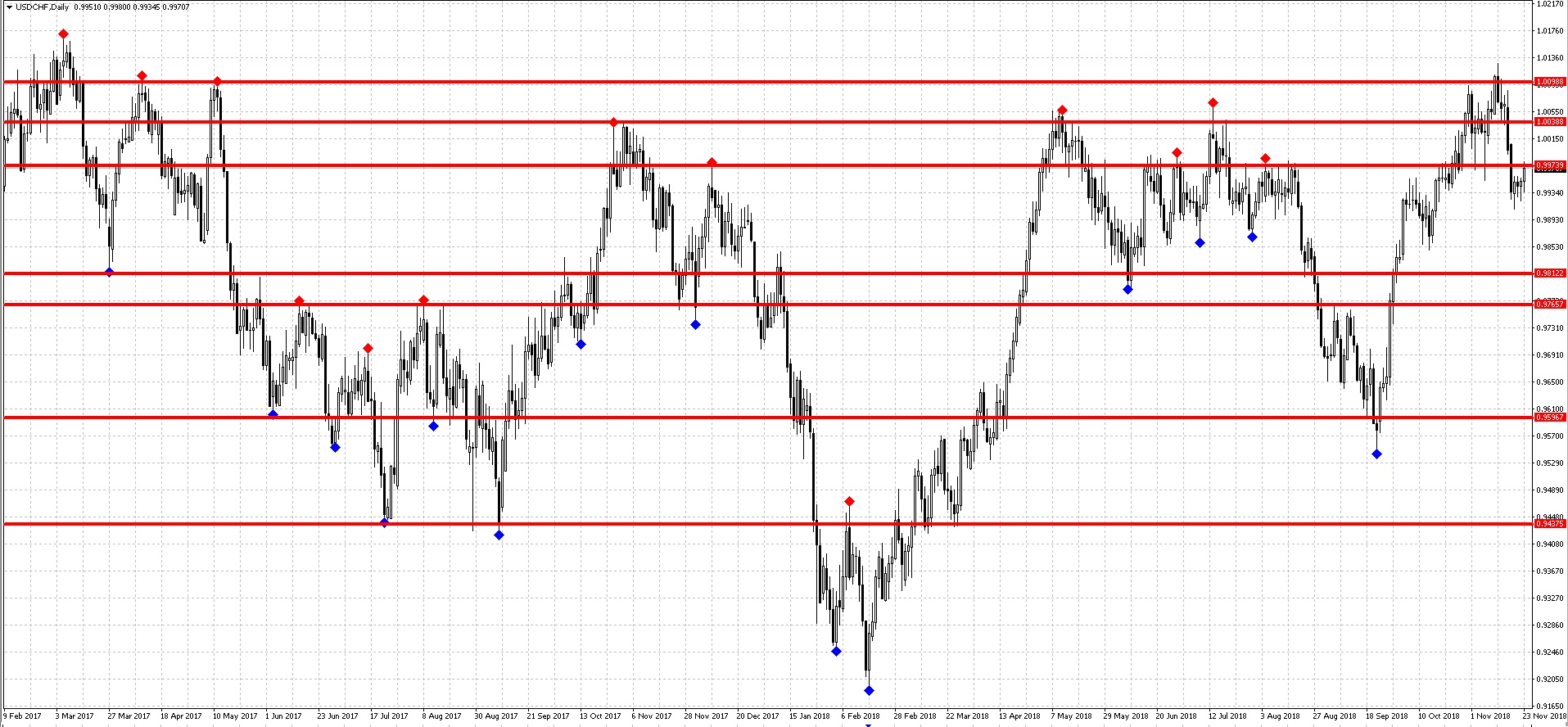
Как видите — график стал лучше и остались действительно значимые экстремумы, через которые можно провести вполне пригодные для торговли уровни. Обратите внимание на то, как цена «уважает» и отрабатывает эти уровни. Уверен, что в будущем, когда цена к ним подойдет, мы вновь увидим реакцию на них.
Фракталы и линии тренда
Еще один довольно неплохой метод применения индикатора fractals — определение опорных точек для построения линий тренда:
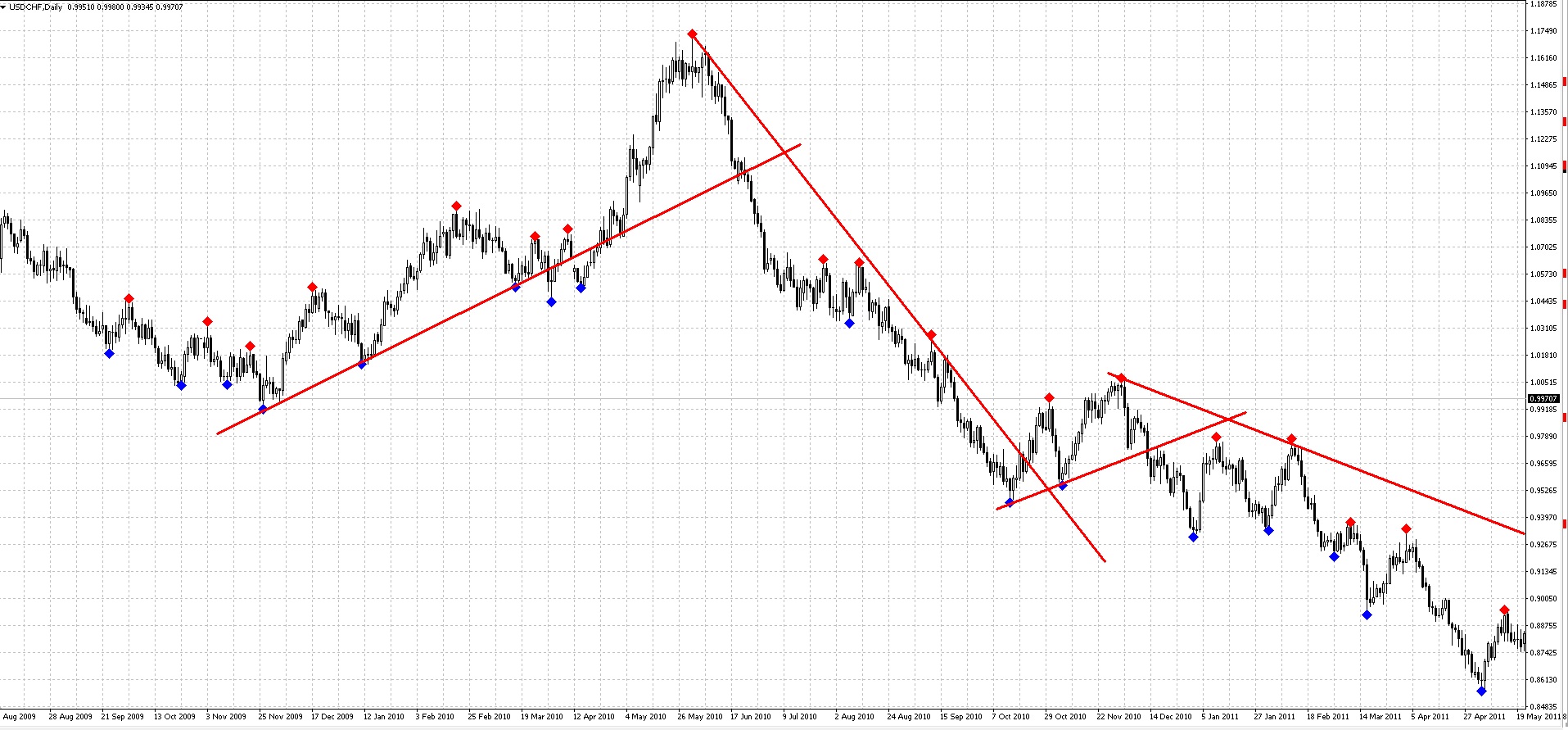
Я накинул индикатор на график, увеличив в настройках число баров. Далее провел несколько линий тренда через некоторые фракталы. Действительно, линии получились вполне интересными, и цена с ними взаимодействует. Естественно, базовые знания в области технического анализа и построения трендовых линий у трейдера должны быть. Но, уверен, что начинающему валютному спекулянту этот индикатор станет хорошим подспорьем в практике.
Определение тренда с помощью индикатора
С помощью фракталов мы также можем определить господствующий тренд на рынке. Сделать это очень просто. Если мы с Вами вспомним определение тренда, которое гласит, что восходящий тренд — это последовательность растущих локальных максимумов и минимумов, а нисходящий — последовательность снижающихся экстремумов. Накинем на график наш индикатор и увидим, что в восходящем тренде фракталы на покупку будут обновляться (пробиваться) чаще, чем фракталы на продажу.
Определение флетового движения
Если цена не смогла преодолеть предыдущий фрактал, это может послужить сигналом начала флетового движения. Для подтверждения сигнала необходимо дождаться формирования противоположного фрактала.
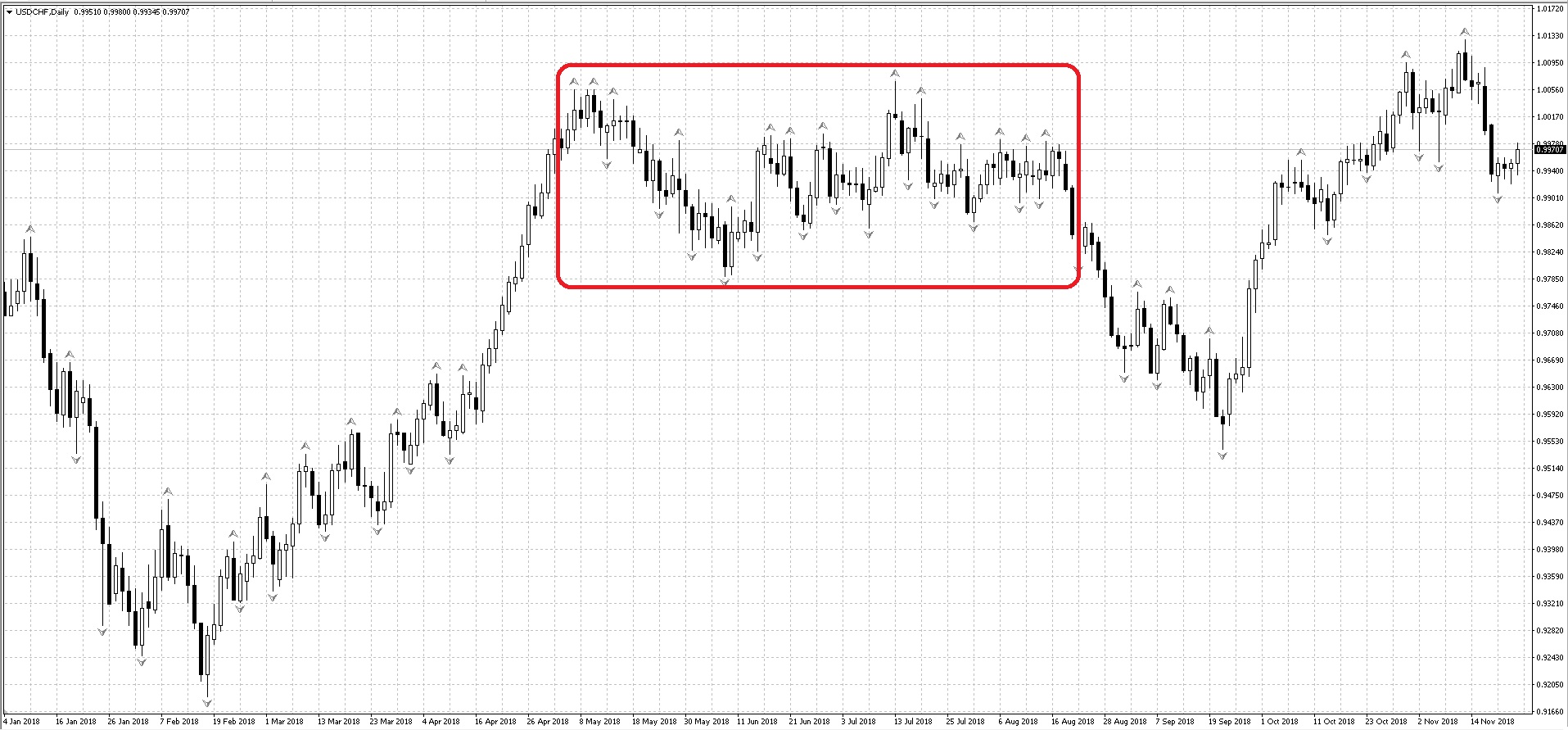
Если он также не смог пробить предыдущий фрактал, то следует ожидать флет в диапазоне между верхним и нижним фракталами, который закончиться после пробития ценой одного из этих уровней.
Заключение
Индикатор Фрактал и его модификации строят на графике множество потенциальных точек входа на любой вкус, большинство из них кажется вполне надежными. На самом деле данная методика анализа не так проста и однозначна. Новичкам не рекомендуется использовать её как единственный фактор для принятия решения.
Фракталами нельзя пользоваться для прогноза цен. Даже Вильямс считал их, как минимум, только третьим подтверждающим фактором. Обратите внимание, что стандартный индикатор Фрактал, входящий в базовый набор торговых платформ, не имеет параметров, поэтому выбирайте модификации, где меняется количество расчетных баров. Так вы сможете более точно настроиться под конкретный актив.
Использование будет иметь положительный результат только в сочетании с другими индикаторами на временных промежутках от часа и выше. Стратегии, включающие в себя индикатор Fractals, обязательно должны анализировать несколько таймфреймов. Тем не менее, не стоит сбрасывать этот индикатор со счетов.
Фракталы применяются на финансовых рынках уже довольно давно – даже в классических торговых стратегиях есть упоминания о них. Например, известная торговая стратегия Билла Вильямса Profitunity использует фракталы как один из элементов системы. Сегодня этот индикатор — герой нашего обзора: мы узнаем историю его появления, посмотрим, какие бывают фракталы, а в теме на форуме вы сможете ознакомиться более чем с сотней разновидностей этого индикатора)
Что такое фрактал?
У понятия «фрактал» нет строгого определения. Поэтому это слово не является математическим термином. Обычно так называют геометрическую фигуру, которая удовлетворяет одному или нескольким из следующих свойств:
— обладает сложной структурой при любом увеличении;
— является (приближенно) самоподобной;
— обладает дробной хаусдорфовой (фрактальной) размерностью, которая больше топологической;
— может быть построена рекурсивными процедурами.
История возникновения
На рубеже XIX и XX веков изучение фракталов носило скорее эпизодический, нежели систематический характер. Раньше математики, в основном, изучали объекты, которые поддавались исследованию при помощи общих методов и теорий.
В 1872 году немецкий математик Карл Вейерштрасс построил пример непрерывной функции, которая нигде не дифференцируема. Однако его построение было целиком абстрактно и трудно для восприятия. Поэтому в 1904 году швед Хельге фон Кох придумал непрерывную кривую, которая нигде не имеет касательной, причем ее довольно просто нарисовать. Оказалось, что она обладает свойствами фрактала. Один из вариантов этой кривой носит название «снежинка Коха».
Идеи самоподобия фигур подхватил француз Поль Пьер Леви, будущий наставник Бенуа Мандельброта. В 1938 году вышла его статья «Плоские и пространственные кривые и поверхности, состоящие из частей, подобных целому», в которой описан еще один фрактал — С-кривая Леви. Все эти вышеперечисленные фракталы можно условно отнести к одному классу конструктивных (геометрических) фракталов.
Другой класс — динамические, или алгебраические фракталы, к которым относится и множество Мандельброта. Первые исследования в этом направлении относятся к началу XX века и связаны с именами французских математиков Гастона Жюлиа и Пьера Фату. В 1918 году вышел почти двухсотстраничный труд Жюлиа, посвященный итерациям комплексных рациональных функций, в котором описаны множества Жюлиа — целое семейство фракталов, близко связанных с множеством Мандельброта. Этот труд был удостоен приза Французской академии, однако в нем не содержалось ни одной иллюстрации, так что оценить красоту открытых объектов было невозможно. Несмотря на то, что это работа прославила Жюлиа среди математиков того времени, о ней довольно быстро забыли.
Вновь внимание к работам Жюлиа и Фату обратилось лишь полвека спустя, с появлением компьютеров: именно они сделали видимыми богатство и красоту мира фракталов. Ведь Фату никогда не мог посмотреть на изображения, которые мы сейчас знаем, как изображения множества Мандельброта, потому что необходимое количество вычислений невозможно провести вручную. Первым, кто использовал для этого компьютер, был Бенуа Мандельброт.
В 1982 году вышла книга Мандельброта «Фрактальная геометрия природы», в которой автор собрал и систематизировал практически всю имевшуюся на тот момент информацию о фракталах и в легкой и доступной манере изложил ее. Основной упор в своем изложении Мандельброт сделал не на тяжеловесные формулы и математические конструкции, а на геометрическую интуицию читателей.
Благодаря иллюстрациям, полученным при помощи компьютера и историческим байкам, которыми автор умело разбавил научную составляющую монографии, книга стала бестселлером, а фракталы стали известны широкой публике. Их успех среди не математиков во многом обусловлен тем, что с помощью весьма простых конструкций и формул, которые способен понять и старшеклассник, получаются удивительные по сложности и красоте изображения.
Когда персональные компьютеры стали достаточно мощными, то появилось даже целое направление в искусстве — фрактальная живопись, причем заниматься ею мог практически любой владелец компьютера. Сейчас в интернете можно легко найти множество сайтов, посвященных этой тематике.
После этого краткого экскурса в историю давайте, теперь, ознакомимся с классификацией типов фракталов на сегодняшний день.
Геометрические фракталы
Именно с них, как вы уже поняли, и начиналась история фракталов. Этот тип фракталов получается путем простых геометрических построений. Сначала изображается основа. Затем некоторые части основы заменяются на фрагмент. На каждом следующем этапе части уже построенной фигуры, аналогичные замененным частям основы, вновь заменяются на фрагмент, взятый в подходящем масштабе. Всякий раз масштаб уменьшается. Когда изменения становятся визуально незаметными, считают, что построенная фигура хорошо приближает фрактал и дает представление о его форме. Для получения самого фрактала нужно бесконечное число этапов. Меняя основу и фрагмент — можно получить много разных геометрических фракталов.
Геометрические фракталы хороши тем, что, с одной стороны, являются предметом достаточного серьезного научного изучения, а с другой стороны — их можно увидеть. Даже человек, далекий от математики, найдет в них что-то для себя. Такое сочетание редко в современной математике, где все объекты задаются с помощью непонятных слов и символов.
Многие геометрические фракталы можно нарисовать буквально на листочке бумаги в клетку. Важно понимать, что все получаемые изображения являются лишь конечными приближениями бесконечных, по своей сути, фракталов. Но всегда можно нарисовать такое приближение, что глаз не будет различать совсем мелкие детали и наше воображение сможет создать верную картину фрактала.
Например, имея достаточно большой лист миллиметровой бумаги и запас свободного времени, можно вручную нарисовать такое точное приближение к ковру Серпинского, что с расстояния в несколько метров невооруженный глаз будет воспринимать его как настоящий фрактал. Компьютер позволит сэкономить время и бумагу и при этом еще увеличить точность рисования.
Снежинка Коха
Это один из самых первых исследованных учеными фракталов. Снежинка получается из трех копий кривой Коха, которая впервые появилась в статье шведского математика Хельге фон Коха в 1904 году. Эта кривая была придумана как пример непрерывной линии, к которой нельзя провести касательную ни в одной точке. Линии с таким свойством были известны и раньше, но кривая Коха замечательна простотой своей конструкции.
Кривая Коха непрерывна, но нигде не дифференцируема. Грубо говоря, именно для этого она и была придумана — как пример такого рода математических «уродцев».

Кривая Коха имеет бесконечную длину. Пусть длина исходного отрезка равна 1. На каждом шаге построения мы заменяем каждый из составляющих линию отрезков на ломаную, которая в 4/3 раза длиннее. Значит, и длина всей ломаной на каждом шаге умножается на 4/3: длина линии с номером n равна (4/3)n–1. Поэтому предельной линии ничего не остается, кроме как быть бесконечно длинной.



Снежинка Коха ограничивает конечную площадь. И это при том, что ее периметр бесконечен. Это свойство может показаться парадоксальным, но оно очевидно — снежинка полностью помещается в круг, поэтому ее площадь заведомо ограничена. Площадь можно посчитать, и для этого даже не нужно особых знаний — формулы площади треугольника и суммы геометрической прогрессии проходят в школе.
Снежинка Коха «наоборот»
Снежинка Коха «наоборот» получается, если строить кривые Коха внутрь исходного равностороннего треугольника.

Линии Чезаро
Вместо равносторонних треугольников используются равнобедренные с углом при основании от 60° до 90°. На рисунке ниже угол равен 88°.

Квадратный вариант
Тут достраиваются квадраты.
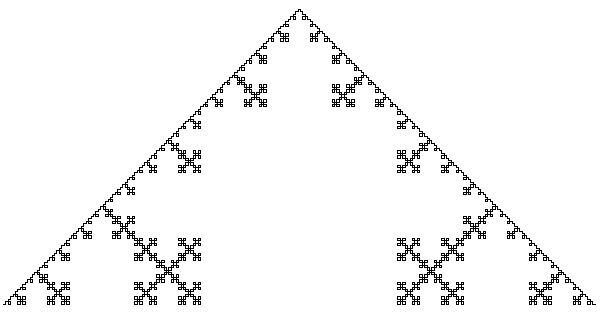
Пирамида Коха

Т-квадрат
Построение начинается с единичного квадрата. Первый шаг: закрасить в центре белым цветом квадрат со стороной 1/2. Затем нужно мысленно разделить квадрат на 4 одинаковых и в центре каждого из них закрасить квадрат со стороной 1/4. Дальше каждый из этих 4 квадратов снова делится на 4 части, всего получится 16 квадратиков, и с каждым из них нужно проделать то же самое. И так далее.

Фрактальная размерность закрашена белым и равна log24 = 2. Она всюду плотна в исходном квадрате. Это означает, что какую бы точку квадрата мы ни взяли, в любой, сколь угодно малой ее окрестности найдутся закрашенные точки. То есть в итоге почти всё стало белым — площадь остатка равна 0, а фрактал занимает площадь 1. Зато длина границы закрашенной части бесконечна.
H-фрактал
Всё начинается с фигуры в виде буквы Н, у которой вертикальные и горизонтальные отрезки равны. Затем к каждому из 4 концов фигуры пририсовывается ее копия, уменьшенная в два раза. К каждому концу (их уже 16) пририсовывается копия буквы Н, уменьшенная уже в 4 раза. И так далее. В пределе получится фрактал, который визуально почти заполняет некоторый квадрат. Н-фрактал всюду плотен в нём. То есть в любой окрестности любой точки квадрата найдутся точки фрактала. Очень похоже на то, что происходит с Т-квадратом. Это не случайно, ведь, если присмотреться, видно, что каждая буква Н содержится в своем маленьком квадратике, который был дорисован на таком же шаге.

Можно сказать (и доказать), что Н-фрактал заполняет свой квадрат (англ. space-filling curve). Поэтому его фрактальная размерность равна 2. Суммарная длина всех отрезков при этом бесконечна.
Принцип построения Н-фрактала применяют при производстве электронных микросхем: если нужно, чтобы в сложной схеме большое число элементов получило один и тот же сигнал одновременно, то их можно расположить в концах отрезков подходящей итерации Н-фрактала и соединить соответствующим образом.
Дерево Мандельброта
Дерево Мандельброта получается, если рисовать толстые буквы Н, состоящие из прямоугольников, а не из отрезков:

Дерево Пифагора
Называется так потому, что каждая тройка попарно соприкасающихся квадратов ограничивает прямоугольный треугольник и получается картинка, которой часто иллюстрируют теорему Пифагора — «пифагоровы штаны во все стороны равны».

Хорошо видно, что всё дерево ограничено. Если самый большой квадрат единичный, то дерево поместится в прямоугольник 6 × 4. Значит, его площадь не превосходит 24. Но, с другой стороны, каждый раз добавляется в два раза больше троек квадратиков, чем в предыдущий, а их линейные размеры в √2 раз меньше. Поэтому на каждом шаге добавляется одна и та же площадь, которая равна площади начальной конфигурации, то есть 2. Казалось бы, тогда площадь дерева должна быть бесконечна! Но, на самом деле, противоречия здесь нет, потому что довольно быстро квадратики начинают перекрываться и площадь прирастает не так быстро. Она всё-таки конечна, но, по всей видимости, до сих пор точное значение неизвестно, и это открытая проблема.
Если менять углы при основании треугольника, то будут получаться немного другие формы дерева. А при угле 60° все три квадрата окажутся равными, а дерево превратится в периодический узор на плоскости:

Можно даже заменять квадраты на прямоугольники. Тогда дерево будет больше похоже на настоящие деревья. А при некоторой художественной обработке получаются довольно реалистичные изображения.
Кривая Пеано
Впервые такой объект появился в статье итальянского математика Джузеппе Пеано в 1890 году. Пеано пытался найти хоть сколько-нибудь наглядное объяснение того, что отрезок и квадрат равномощны (если рассматривать их как множества точек), то есть в них «одинаковое» количество точек. Эта теорема была ранее доказана Георгом Кантором в рамках придуманной им теории множеств. Однако подобные противоречащие интуиции результаты вызывали большой скепсис по отношению к новой теории. Пример Пеано — построение непрерывного отображения из отрезка на квадрат — стал хорошим подтверждением правоты Кантора.

Любопытно, что в статье Пеано не было ни одной иллюстрации. Иногда выражение «кривая Пеано» относят не к конкретному примеру, а к любой кривой, которая заполняет часть плоскости или пространства.
Кривая Гильберта

Эта кривая (кривая Гильберта) была описана Давидом Гильбертом в 1891 году. Мы можем увидеть лишь конечные приближения к тому математическому объекту, который имеется в виду — сам он получится в пределе только после бесконечного числа операций.
Фрактал «Греческий крест»
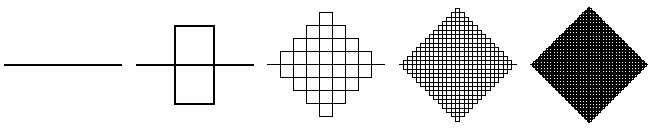
Еще один интересный пример — фрактал «Греческий крест».
Кривая Госпера

Кривая Госпера, или снежинка Госпера – еще одна из вариаций кривых линий.
Кривая Леви
Хотя этот объект изучал еще итальянец Эрнесто Чезаро в 1906 году, его самоподобие и фрактальные свойства исследовал в 1930-х годах француз Поль Пьер Леви. Фрактальная размерность границы этого фрактала примерно равна 1,9340. Но это довольно сложный математический результат, а точное значение неизвестно.

За сходство с буквой «С», написанной витиеватым шрифтом, ее еще называют С-кривой Леви. Если приглядеться, то можно заметить, что кривая Леви похожа на форму кроны дерева Пифагора.
Куб Гильберта
А есть еще и трехмерные аналоги таких линий. Например, трехмерная кривая Гильберта, или куб Гильберта.

Элегантная металлическая версия трехмерной кривой Гильберта (третья итерация), созданная профессором компьютерных наук Калифорнийского университета в Беркли Карло Секином.
Треугольник Серпинского

Этот фрактал описал в 1915 году польский математик Вацлав Серпинский. Чтобы его получить, нужно взять равносторонний треугольник с внутренностью, провести в нём средние линии и выкинуть центральный из четырех образовавшихся маленьких треугольников. Дальше эти же действия нужно повторить с каждым из оставшихся трех треугольников, и т.д. На рисунке показаны первые три шага, а на флэш-демонстрации вы можете потренироваться и получить шаги вплоть до десятого.

Выкидывание центральных треугольников — не единственный способ получить в итоге треугольник Серпинского. Можно двигаться «в обратном направлении»: взять изначально «пустой» треугольник, затем достроить в нём треугольник, образованный средними линиями, затем в каждом из трех угловых треугольников сделать то же самое, и т.д. Поначалу фигуры будут сильно отличаться, но с ростом номера итерации они будут всё больше походить друг на друга, а в пределе совпадут.

Следующий способ получить треугольник Серпинского еще больше похож на обычную схему построения геометрических фракталов с помощью замены частей очередной итерации на масштабированный фрагмент. Здесь на каждом шаге составляющие ломаную отрезки заменяются на ломаную из трех звеньев (она сама получается в первой итерации). Откладывать эту ломаную нужно попеременно то вправо, то влево. Видно, что уже восьмая итерация очень близка к фракталу, и чем дальше, тем ближе будет подбираться к нему линия.
Ковер (квадрат, салфетка) Серпинского
На треугольниках уважаемый математик не остановился и 1916 году им была описана квадратная версия. Ему удалось доказать, что любая кривая, которую можно нарисовать на плоскости без самопересечений, гомеоморфна какому-то подмножеству этого дырявого квадрата. Как и треугольник, квадрат можно получить из разных конструкций. Справа изображен классический способ: разделение квадрата на 9 частей и выбрасывание центральной части. Затем то же повторяется для оставшихся 8 квадратов, и т.д.

Как и у треугольника, у квадрата нулевая площадь. Фрактальная размерность ковра Серпинского равна log38, вычисляется аналогично размерности треугольника.
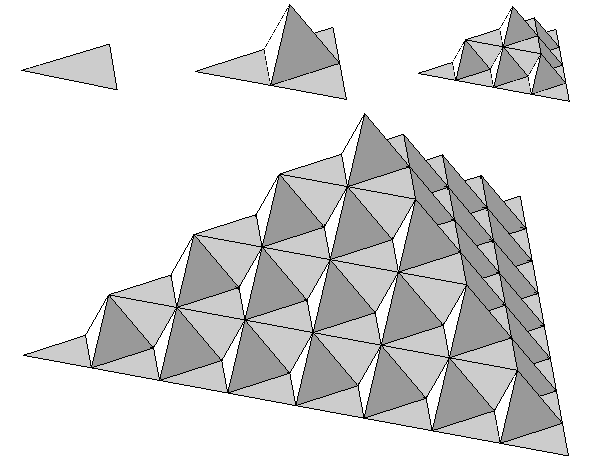
Пирамида Серпинского

Один из трехмерных аналогов треугольника Серпинского. Строится аналогично, с учетом трехмерности происходящего: 5 копий начальной пирамиды, сжатой в два раза, составляют первую итерацию, ее 5 копий составят вторую итерацию и так далее. Фрактальная размерность равна log25. У фигуры нулевой объем (на каждом шаге половина объема выбрасывается), но при этом площадь поверхности сохраняется от итерации к итерации, и у фрактала она такая же, как и у начальной пирамиды.
Губка Менгера
Обобщение ковра Серпинского в трехмерное пространство. Чтобы построить губку, нужно бесконечное повторение процедуры: каждый из кубиков, из которых состоит итерация, делится на 27 втрое меньших кубиков, из которых выбрасывают центральный и его 6 соседей. То есть каждый кубик порождает 20 новых, в три раза меньших. Поэтому фрактальная размерность равна log320. Этот фрактал является универсальной кривой: любая кривая в трехмерном пространстве гомеоморфна некоторому подмножеству губки. У губки нулевой объем (так как на каждом шаге он умножается на 20/27), но при этом бесконечно большая площадь.

Геометрических фракталов имеется еще огромное множество, а площадь поверхности этой странички, к сожалению, не бесконечна. Поэтому давайте перейдем к следующему типу фракталов – алгебраическому.
Динамические (алгебраические) фракталы
Фракталы этого типа возникают при исследовании нелинейных динамических систем (отсюда и название). Поведение такой системы можно описать комплексной нелинейной функцией (многочленом) f(z).
Множества Жюлиа
Возьмем какую-нибудь начальную точку z0 на комплексной плоскости. Теперь рассмотрим бесконечную последовательность чисел на комплексной плоскости, каждое следующее из которых получается из предыдущего: z0, z1 = f(z0), z2 = f(z1), … zn+1 = f(zn). В зависимости от начальной точки z0 такая последовательность может вести себя по-разному: стремиться к бесконечности при n → ∞; сходиться к какой-то конечной точке; циклически принимать ряд фиксированных значений; возможны и более сложные варианты.
Таким образом, любая точка z комплексной плоскости имеет свой характер поведения при итерациях функции f(z), а вся плоскость делится на части. При этом точки, лежащие на границах этих частей, обладают таким свойством: при сколь угодно малом смещении характер их поведения резко меняется (такие точки называют точками бифуркации). Так вот, оказывается, что множества точек, имеющих один конкретный тип поведения, а также множества бифуркационных точек часто имеют фрактальные свойства. Это и есть множества Жюлиа для функции f(z).
Множество Мандельброта
Оно строится немного иначе. Рассмотрим функцию fc(z) = z2 + с, где c — комплексное число. Построим последовательность этой функции с z0 = 0, в зависимости от параметра с она может расходиться к бесконечности или оставаться ограниченной. При этом все значения с, при которых эта последовательность ограничена, как раз и образуют множество Мандельброта. Оно было детально изучено самим Мандельбротом и другими математиками, которые открыли немало интересных свойств этого множества.
Видно, что определения множеств Жюлиа и Мандельброта похожи друг на друга. На самом деле эти два множества тесно связаны. А именно, множество Мандельброта — это все значения комплексного параметра c, при которых множество Жюлиа fc(z) связно (множество называется связным, если его нельзя разбить на две непересекающиеся части, с некоторыми дополнительными условиями).
Фрактал Галлея
Такие фракталы получаются, если в качестве правила для построения динамического фрактала использовать формулу Галлея для поиска приближенных значений корней функции. Формула довольно громоздкая, так что кто хочет, может посмотреть ее в Википедии. Идея метода почти та же, что используется для рисования динамических фракталов: берем какое-нибудь начальное значение (как обычно, здесь речь идет о комплексных значениях переменных и функций) и применяем к нему много раз формулу, получая последовательность чисел. Почти всегда она сходится к одному из нулей функции (то есть значению переменной, при котором функция принимает значение 0). Метод Галлея, несмотря на громоздкость формулы, работает эффективнее метода Ньютона: последовательность сходится к нулю функции быстрее.
Фрактал Ньютона
Еще один тип динамических фракталов составляют фракталы (так называемые бассейны) Ньютона. Формулы для их построения основаны на методе решения нелинейных уравнений, который был придуман великим математиком еще в XVII веке. Применяя общую формулу метода Ньютона zn+1 = zn – f(zn)/f'(zn), n = 0, 1, 2, … для решения уравнения f(z) = 0 к многочлену zk – a, получим последовательность точек: zn+1 = ((k – 1)znk – a)/kznk–1, n = 0, 1, 2, … . Выбирая в качестве начальных приближений различные комплексные числа z0, будем получать последовательности, которые сходятся к корням этого многочлена. Поскольку корней у него ровно k, то вся плоскость разбивается на k частей — областей притяжения корней. Границы этих частей имеют фрактальную структуру (заметим в скобках, что если в последней формуле подставить k = 2, а в качестве начального приближения взять z0 = a, то получится формула, которую реально используют для вычисления квадратного корня из a в компьютерах). Наш фрактал получается из многочлена f(z) = z3 – 1.
Применение фракталов в промышленности и быту
Ученые – очень увлеченные личности. Их хлебом не корми, дай пофантазировать на абстрактные темы. Но мы с вами люди практичные, и, прочитав все то, что написано выше, у многих уже наверняка возник резонный вопрос: «ну и че?». Так вот, что же все-таки привнесло это знание в мир?
Во-первых, фракталы используются в компьютерных системах, причем очень плотно. Наиболее полезным использованием фракталов в компьютерной науке является фрактальное сжатие данных. В основе этого вида сжатия лежит тот факт, что реальный мир хорошо описывается фрактальной геометрией. При этом картинки сжимаются гораздо лучше, чем это делается обычными методами (такими как jpeg или gif). Другое преимущество фрактального сжатия в том, что при увеличении картинки не наблюдается эффекта пикселизации (увеличения размеров точек до размеров, искажающих изображение). При фрактальном же сжатии, после увеличения, картинка часто выглядит даже лучше, чем до него.
Во-вторых, это механика жидкостей и, как следствие, нефтяная промышленность. Дело в том, что изучение турбулентности в потоках очень хорошо подстраивается под фракталы. Турбулентные потоки хаотичны и поэтому их сложно точно смоделировать. И здесь помогает переход к их фрактальному представлению, что сильно облегчает работу инженерам и физикам, позволяя им лучше понять динамику сложных потоков. При помощи фракталов также можно смоделировать языки пламени. Пористые материалы хорошо представляются во фрактальной форме в связи с тем, что они имеют очень сложную геометрию. Это используется в нефтяной науке.
В-третьих, приходя вечером с завода домой, ложась на любимый боевой диван, вы включаете телевизор, который тоже имеет отношение к фракталам. Дело в том, что для передачи данных на расстояния используются антенны, имеющие фрактальные формы, что сильно уменьшает их размеры и вес.
Использование фрактальной геометрии при проектировании антенных устройств было впервые применено американским инженером Натаном Коэном, который жил тогда в центре Бостона, где была запрещена установка на зданиях внешних антенн. Коэн вырезал из алюминиевой фольги фигуру в форме кривой Коха и затем наклеил ее на лист бумаги, а затем присоединил к приемнику. Оказалось, что такая антенна работает не хуже обычной. И хотя физические принципы такой антенны не изучены до сих пор, это не помешало Коэну обосновать собственную компанию и наладить их серийный выпуск. В данный момент американская фирма Fractal Antenna System разработала антенну нового типа. Теперь можно отказаться от использования в мобильных телефонах торчащих наружных антенн — так называемая фрактальная антенна располагается прямо на основной плате внутри аппарата.
Кроме того, фракталы используются для описания кривизны поверхностей. Неровная поверхность характеризуется комбинацией из двух разных фракталов. Еще они используются в разработке биосенсорных взаимодействий, исследованиях биения сердца, моделировании хаотических процессов, в частности при описании моделей популяций животных и так далее.
Фрактальная структура рынка
Вся эта ода фракталам была бы напрасной, если бы не фрактальная природа финансовых рынков. Да, наконец мы дошли до обсуждения того самого вопроса, ради которого я эту статью и писал.
Итак, в настоящее время применяется много способов анализа финансовых рынков, на основе которых трейдеры создают свои торговые стратегии. Среди различных инструментов анализа и прогноза фрактальный анализ стоит немного в стороне. Это отдельная разносторонняя и интересная теория для обсуждения и изучения. Первое впечатление говорит о простоте тематики, однако копни глубже, и будет видно много скрытых нюансов.
Понимание фракталов — это ключ к видению скрытой информации о рынке. А ведь именно она является одним из ключевых факторов рыночного успеха спекулянта и залогом большой стабильной прибыли.
14 октября 2010 года ушел из жизни Бенуа Мандельброт — человек, во многом изменивший наше представление об окружающих нас предметах и обогативший наш язык словом «фрактал».

Как вы уже знаете, именно благодаря Мандельброту мы знаем, что фракталы окружают нас повсюду. Некоторые из них непрерывно меняются, как движущиеся облака или пламя, в то время как другие, подобно береговым линиям, деревьям или нашим сосудистым системам — сохраняют структуру, приобретенную в процессе эволюции. При этом реальный диапазон масштабов, где наблюдаются фракталы, простирается от расстояний между молекулами в полимерах до расстояния между скоплениями галактик во Вселенной. Богатейшая коллекция таких объектов собрана в знаменитой книге Мандельброта «Фрактальная геометрия природы».
Важнейшим классом природных фракталов являются хаотические временные ряды, или упорядоченные во времени наблюдения характеристик различных природных, социальных и технологических процессов. Среди них имеются как традиционные (геофизические, экономические, медицинские), так и те, которые стали известными относительно недавно (ежедневные колебания уровня преступности или ДТП в регионе, изменения количества показов определенных сайтов в интернете и т.д.). Эти ряды, обычно, порождаются сложными нелинейными системами, которые имеют самую различную природу. Однако у всех характер поведения повторяется на разных масштабах. Наиболее популярными их представителями являются финансовые временные ряды (в первую очередь цены акций и курсы валют).
Самоподобная структура таких рядов известна очень давно. В одной из своих статей Мандельброт писал, что его интерес к котировкам на фондовом рынке начался с высказывания одного из биржевиков: «…Движения цен большинства финансовых инструментов внешне похожи на разных масштабах времени и цены. По внешнему виду графика наблюдатель не может сказать, относятся данные к недельным, дневным или же часовым изменениям».
Мандельброт, занимающий совершенно особое место в финансовой науке, имел славу «ниспровергателя основ», вызывая среди экономистов явно неоднозначное к себе отношение. С момента возникновения современной финансовой теории, основанной на концепции общего равновесия, он был одним из главных ее критиков и до конца жизни пытался найти ей приемлемую альтернативу. Однако именно Мандельброт разработал систему понятий, которая при соответствующей модификации, как оказалось, позволяет не только построить эффективный прогноз, но и предложить, видимо, единственное на данный момент эмпирическое обоснование классической теории финансов.
Основной характеристикой фрактальных структур является фрактальная размерность D, введенная Феликсом Хаусдорфом в 1919 году. Для временных рядов чаще используют индекс Херста H, который связан с фрактальной размерностью соотношением D = 2 – H и является показателем персистентности (способности сохранять определенную тенденцию) временного ряда.
Обычно различают три принципиально разных режима, которые могут существовать на рынке: при Н = 0,5 поведение цен описывается моделью случайного блуждания; при Н > 0,5 цены находятся в состоянии тренда (направленного движения вверх или вниз); при H < 0,5 цены находятся в состоянии флэта, или частых колебаний в достаточно узком диапазоне цен. Однако для надежного вычисления H (так же как и D) требуется слишком много данных, что исключает возможность использования этих характеристик в качестве показателей, определяющих локальную динамику временного ряда.
Как известно, базовой моделью финансовых временных рядов является модель случайного блуждания, впервые полученная Луисом Башелье для описания наблюдений за ценами акций на Парижской фондовой бирже. В результате переосмысления этой модели, которая иногда наблюдается в поведении цен, возникла концепция эффективного рынка, на котором цена в полной мере отражает всю доступную информацию.
Для существования такого рынка достаточно предположить, что на нем действует большое число полностью информированных рациональных агентов, которые мгновенно реагируют на поступающую информацию и корректируют цены, приводя их в состояние равновесия. Все основные результаты классической теории финансов (портфельная теория, модель CAPM, модель Блэка—Шоулза и другие) были получены в рамках именно такого подхода. В настоящее время концепция эффективного рынка продолжает играть доминирующую роль и в финансовой теории, и в финансовом бизнесе.
Тем не менее, к началу 60-х годов прошлого века эмпирические исследования показали, что сильные изменения цен на рынке происходят значительно чаще, чем предсказывала основная модель эффективного рынка (модель случайного блуждания). Одним из первых, кто подверг концепцию эффективного рынка всесторонней критике, был как раз Мандельброт.
Действительно, если корректно вычислить значение показателя H для какой-либо акции, то оно, вероятнее всего, будет отлично от H = 0,5, которое соответствует модели случайного блуждания. Мандельброт нашел все возможные обобщения этой модели, которые могут иметь отношение к реальному поведению цен. Как оказалось, это, с одной стороны, процессы, названные им полетом Леви, а с другой — процессы, которые он назвал обобщенным броуновским движением.
Для описания поведения цен обычно используют концепцию фрактального рынка, которую принято рассматривать в качестве альтернативы эффективному рынку. Концепция предполагает, что на рынке есть широкий спектр агентов с разными инвестиционными горизонтами и, следовательно, разными предпочтениями. Эти горизонты меняются от нескольких минут для внутридневных трейдеров до нескольких лет для крупных банков и инвестиционных фондов.
Устойчивым положением на таком рынке является режим, при котором «средняя доходность не зависит от масштаба, если не считать умножения на соответствующий масштабный коэффициент». Фактически речь идет о целом классе режимов, каждый из которых определяется своим значением показателя H. При этом значение H = 0,5 оказывается одним из многих возможных и, следовательно, равноправным с любым другим значением. Эти и другие близкие соображения стали поводом для серьезных сомнений относительно существования действительного равновесия на фондовом рынке.
Посмотрите на ценовые графики снизу:






Видно, что цена совершает постоянные колебания, образовывая при этом структуру повторяющегося характера. Просматривается она на всех рынках, независимо от временного масштаба.
На изображении представлены графики: BRN M30, BTCUSD H1, DAX30 D1, EURSGD M5, USDCHF H1, XAUUSD M15. Без подписей и разъяснений вряд ли кто-нибудь сможет отличить их друг от друга.
Этих графики не совсем похожи друг на друга, но имеют некоторые общие модели. На заданном промежутке времени цена движется в одном направлении, затем меняет свое направление на обратное и частично восстанавливает предыдущее движение, после вновь разворачивается. Не имеет значения, какой таймфрейм используется для графиков — все они выглядят примерно одинаково (постоянные колебания), так же, как и фракталы.
Колебания образуют волны рынка. Что такое волна? Это импульс и коррекция к нему (движение-разворот-движение в обратном направлении, частично восстанавливающее предыдущее). Такие движения образуют волны.

На изображении показаны эти движения, которые образуют волны. Несколько таких волн образуют большую волну аналогичной формы (импульс-коррекция). Несколько малых волн образуют одну волну среднего размера.

Волны среднего размера образуют одну большую волну. Это и есть суть фрактальной теории на финансовых рынках.
Серии подобных волн образуют направленные движения на рынке – тренды. Подобные тренды, в свою очередь, образуют направленные движения старшего временного порядка. Как и в случае с волнами — небольшие движения образуют одно среднее и т.д. Так различают краткосрочные тренды, среднесрочные и долгосрочные. Это – классическое понимание фрактальной природы рынка.
Фракталы Билла Вильямса
Как я уже говорил, фракталы рынка являются одним из индикаторов в торговой системе Била Вильямса. Считается, что именно он впервые и ввел это название в трейдинг, но, как вы понимаете, это не так. При торговле по фракталам, в сочетании со своим индикатором Аллигатор, автор обнаруживал локальные максимумы или минимумы рынка. Он также писал, что определение фрактальной структуры рынка позволяет найти способ понимания поведения цены.

Вообще же теория фракталов Вильямса в свое время вызвала бурные споры, прежде всего потому, что автор, как считают многие, вставил в свою теорию много научной терминологии (фрактал, аттрактор и так далее) и сделал это не совсем корректно.
Вообще же, фракталы Вильямса появляются на рынке достаточно часто и практически на всех таймфреймах и являются, по сути, простыми локальными экстремумами на отрезке из 5 баров и практически не соответствуют математической теории фракталов. Точно таким же образованием на графике являются и ТД-точки второго порядка Томаса Демарка. Однако, несмотря все эти совпадения — эта теория весьма популярна и до сих пор.
Технический анализ по Вильямсу рассматривает 4 существующих формации фрактала:
истинный фрактал на покупку;
ложный фрактал на покупку;
истинный фрактал на продажу;
ложный фрактал на продажу.

Об истинных и ложных фракталах и о том, как их различать, мы еще поговорим ниже.
Индикатор Fractals в торговом терминале MetaTrader
Индикаторы Билла Вильямса не требуют установки и входят в стандартный набор индикаторов, доступных трейдеру «из коробки». Для того, чтобы прикрепить индикатор фрактал в терминале MetaTrader 4 к графику необходимо: в главном меню (или в окне «Навигатор») выбрать пункт меню «Вставка» — «Индикаторы» — «Билла Вильямса» — «Fractals»:

Стандартный индикатор для МТ4 не имеет никаких настроек, кроме цветовых. Его использование с фиксированным периодом «5» сводит на нет все возможности и преимущества данного инструмента. Но для платформы MetaTrader существует множество пользовательских индикаторов, которые помогут решить эту проблему.
Наш форумчанин Pavel888 как раз собрал большую коллекцию из различных индикаторов Fractals в ветке на форуме, за что ему большое спасибо.
Проблема ложности и истинности фракталов
Во время торговли с использованием фракталов существует один важный нюанс – это появление на графике большого количества сигналов, часть из которых являются ложными. Для их фильтрации Билл Вильямс разработал еще один индикатор под названием «Аллигатор», который также можно найти в стандартном наборе индикаторов в MT4.
Проблема ложных фракталов является основным источником ошибок, аналогично оценкам истинности пробоя поддержки/сопротивления. Независимо от конкретной методики общий принцип определения надежности следующий – любые отклонения от классического вида должны вызвать сомнения. Как и во всем теханализе уменьшение таймфрейма приводит к увеличению ложных сигналов и загромождению графика. Примеры неустойчивых фракталов приведены на рисунке ниже.

Отрабатывая крупные паттерны, лучше открывать позиции в моменты коррекции последнего ценового импульса, которые находятся в левой части формации. Внутри паттерна надежно работают стандартные Фибоначчи-коррекции на 38% (0,382), 50% (0,500) и 62% (0,618). Если «растягивать» уровни через соседние сигналы индикатора, то можно открываться через лимитные ордера около ключевых уровней.
Таким же образом можно защитить сделку от непредсказуемого обратного пробоя, постепенно перемещая stoploss, для контроля противоположного максимума или минимума последней и предпоследней свечи. Когда структура только формируется, стоп должен быть минимум на 5-10 пунктов выше или ниже последнего сигнала, который дал индикатор Фрактал. Тогда при незначительных откатах мы остаемся в рынке, а если будет полная смена тренда, сделка закроется с минимальным убытком.
Есть еще один способ определить, что перед нами ложные фракталы – когда они пробиты баром с длинной тенью и малым телом (пин-бар). Чем длиннее его «нос», тем сильнее разворотный сигнал, означающий, что рынку не удалось с первого раза перейти уровень последнего паттерна. Если пробой состоялся и следующая свеча закрыта выше High (для продажи) или ниже Low (для покупки) носа, то с большой вероятностью можно пропустить сигнал и подождать следующего. Подобная ситуация может произойти и через 3-5 баров, но обращаем внимание только на бар, пробивший индикатор Fractals.
Практическое использование фракталов
Билл Вильямс советовал использовать фракталы в стратегиях, которые базируются на пробое важных ценовых уровней. Движение цены выше или ниже хотя бы на один пункт от уровня предыдущего фрактала, по мнению автора этого индикатора, уже говорит о пробитии этого уровня ценой.
Пробитие уровня предыдущего фрактала называется прорывом покупателей в случае, если цена поднимается выше предыдущего фрактала, направленного вверх. В обратном случае, когда цена опускается ниже предыдущего фрактала, направленного вниз, говорят о прорыве продавцов. Билл Вильямс советовал расценивать прорыв покупателей или продавцов как сигнал к открытию позиции.
Обычно, трейдеры выставляют отложенные Stop ордера на несколько пунктов выше или ниже фрактала для открытия позиции в случае пробития этого уровня. В таких случаях стоп-лосс, обычно, выставляется на уровне предпоследнего противоположного фрактала.
В классической интерпретации Билл Вильямс советует фильтровать торговые сигналы, подаваемые фракталами, с помощью индикатора «Аллигатор». Так, для открытия позиции на покупку, необходимо, чтобы был пробит фрактал, находящийся выше красной линии (так называемые «Зубы аллигатора»). Автор стратегии советовал входить в рынок сразу после пробития фрактала вверх или же с помощью отложенного ордера BuyStop. Вход в рынок на продажу происходит в случае пробития фрактала, находящегося ниже красной линии.

Более подробно с этой стратегией вы можете ознакомиться в статье про систему Билла Вильямса Profitunity. А мы разберем основные практические способы использования фракталов в отрыве от этой ТС.
Торговля на пробой фрактала
Этот метод классический, предложенный Биллом Вильямсом. Как видно из названия, торговля носит пробойных характер и рассчитана на продолжение текущего тренда. Вход в сделку осуществляется отложенным стоп-ордером на пробой ближайшего к цене фрактала. Пример вы можете видеть на рисунке выше.
Как пишет сам автор, данная методика торговли будет давать много ложных входов, поэтому Билл предлагает фильтровать сигналы с помощью индикатора «Аллигатор». В принципе, индикатор «Аллигатор» можно заменить обычными средними скользящими и также использовать их как фильтр. Но повторюсь, что рассматривать фракталы и «Аллигатор» в отрыве от других инструментов Вильямса не имеет смысла, поэтому мы не будем останавливаться на этом и двинемся дальше.
Фракталы как уровни поддержки/сопротивления
Если Вы хотя бы раз сталкивались с уровнями поддержки/сопротивления, то знаете, насколько сложно их строить, особенно, если вы новичок. И сложность вся эта возникает из-за субъективности этого инструмента. Когда мы строим уровни, то не можем с уверенностью сказать, правильно ли мы построили их или нет. Билл Вильямс со своими фракталами дает нам прекрасный инструмент для поиска и построения значимых уровней поддержки и сопротивления.
Давайте накинем индикатор на какой-нибудь график и проанализируем с точки зрения уровней.

Это график USDCHF D1 с классическим фракталом. Да, график просто пестрит от этих стрелочек. Если через каждый экстремум, выделенный индикатором, провести горизонтальную линию, то за этими линиями станет не видно самого графика.
Давайте увеличим число периодов и посмотрим на результат:

Как видите — график стал лучше и остались действительно значимые экстремумы, через которые можно провести вполне пригодные для торговли уровни. Обратите внимание на то, как цена «уважает» и отрабатывает эти уровни. Уверен, что в будущем, когда цена к ним подойдет, мы вновь увидим реакцию на них.
Фракталы и линии тренда
Еще один довольно неплохой метод применения индикатора fractals — определение опорных точек для построения линий тренда:

Я накинул индикатор на график, увеличив в настройках число баров. Далее провел несколько линий тренда через некоторые фракталы. Действительно, линии получились вполне интересными, и цена с ними взаимодействует. Естественно, базовые знания в области технического анализа и построения трендовых линий у трейдера должны быть. Но, уверен, что начинающему валютному спекулянту этот индикатор станет хорошим подспорьем в практике.
Определение тренда с помощью индикатора
С помощью фракталов мы также можем определить господствующий тренд на рынке. Сделать это очень просто. Если мы с Вами вспомним определение тренда, которое гласит, что восходящий тренд — это последовательность растущих локальных максимумов и минимумов, а нисходящий — последовательность снижающихся экстремумов. Накинем на график наш индикатор и увидим, что в восходящем тренде фракталы на покупку будут обновляться (пробиваться) чаще, чем фракталы на продажу.
Определение флетового движения
Если цена не смогла преодолеть предыдущий фрактал, это может послужить сигналом начала флетового движения. Для подтверждения сигнала необходимо дождаться формирования противоположного фрактала.

Если он также не смог пробить предыдущий фрактал, то следует ожидать флет в диапазоне между верхним и нижним фракталами, который закончиться после пробития ценой одного из этих уровней.
Заключение
Индикатор Фрактал и его модификации строят на графике множество потенциальных точек входа на любой вкус, большинство из них кажется вполне надежными. На самом деле данная методика анализа не так проста и однозначна. Новичкам не рекомендуется использовать её как единственный фактор для принятия решения.
Фракталами нельзя пользоваться для прогноза цен. Даже Вильямс считал их, как минимум, только третьим подтверждающим фактором. Обратите внимание, что стандартный индикатор Фрактал, входящий в базовый набор торговых платформ, не имеет параметров, поэтому выбирайте модификации, где меняется количество расчетных баров. Так вы сможете более точно настроиться под конкретный актив.
Использование будет иметь положительный результат только в сочетании с другими индикаторами на временных промежутках от часа и выше. Стратегии, включающие в себя индикатор Fractals, обязательно должны анализировать несколько таймфреймов. Тем не менее, не стоит сбрасывать этот индикатор со счетов.
Не является индивидуальной инвестиционной рекомендацией | При копировании ссылка обязательна | Нашли ошибку - выделить и нажать Ctrl+Enter | Жалоба

