17 октября 2022 Доходъ
В этой статье мы постараемся просто (на сколько это возможно) обсудить риски изменения процентных ставок, возникающие при инвестициях в облигации. Для этого попробуем решить следующую задачку (непонятные термины объяснены ниже):

Голосование по ответам на задачку в нашем канале в Telegram @dohod
Из условий задачи видно, что она не требует точных расчетов. Изменение стоимости портфелей A и B, конечно, зависит от множества параметров: величины купонов и частоты их выплат для каждой облигации, точного срока погашения, текущей формы кривой процентных ставок, кредитного качества, кредитных спредов и т.д.
Здесь нам необходимо логически оценить наиболее вероятное влияние изменений процентных ставок на цену облигаций (процентный риск) и портфелей в целом, используя соответствующие параметры (дюрацию и выпуклость).
Если вы держите облигации до погашения, то у вас нет никакого риска процентных ставок. Если эмитент не подведет, то вы получите все купонные платежи и сумму номинала при погашении независимо от изменения рыночных процентных ставок. Но если деньги могут понадобиться вам раньше, то этот риск для вас актуален.
Дюрация (duration)
Справедливая цена облигации в любой момент времени равна сумме дисконтированных денежных потоков, которая она генерирует (купонов и сумм погашения). Зная цену облигации, легко (относительно) рассчитать ее доходность к погашению.
Если мы рассчитаем доходность облигации при падении ее цены на X рублей, то разница межу получившейся и начальной доходностью будет разной для разных облигаций (в основном из-за разницы в сроках до погашения и размерах купонов).
Значит, и наоборот, изменение на Y% доходности будет отражаться на разном изменении их цены. Чем больше такие изменения, тем больше чувствительность цены облигации к изменению процентных ставок (то есть, больше риск облигации). Именно это и отражает дюрация (D).
Дюрация, как и эффективная доходность к погашению (YTM) позволяет сравнивать друг с другом облигации, имеющие различные характеристики (срок, размер купонов, периодичность выплат и пр.). Классическая дюрация (дюрация Маколея) – это срок (в днях или годах), когда вложения в облигацию окупятся (но лучше воспринимать его как риск, описанный выше).
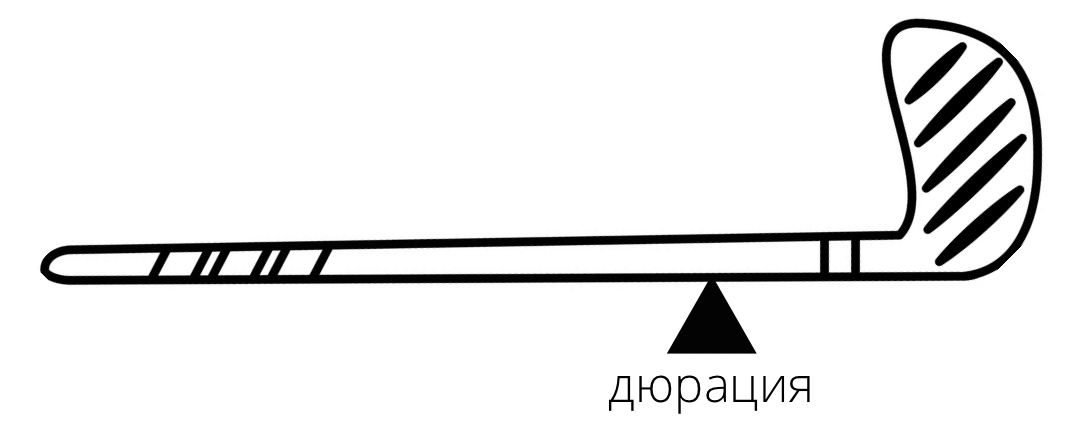
Дюрация - как точка опоры, уравновешивающая все дисконтированные платежи по облигации.
Очевидно, что чем больше срок до погашения облигации, тем выше ее риск, связанный с изменением процентных ставок. Длинные облигации (10,20 лет и более) имеют такой высокий риск, что часто ведут себя как акции с точки зрения волатильности (изменения цен).
В случае нашей задачки дюрация Портфеля A и Портфеля B одинакова и составляет 3 года (для Портфеля B = 0.5*50% + 5.5*50%). То есть, несмотря на то, что Портфель B состоит из двух облигаций с дюрациями 0.5 и 5.5 лет, он подвержен влиянию изменения процентных ставок в той же степени, что и Портфель A (на самом деле, не совсем - об этом ниже).
Модифицированная дюрация (MD), рассчитывается как D/(1+доходность) и измеряет примерное относительное (в %) изменение цены облигации при изменении процентной ставки на 1% годовых (100 базисных пунктов).
Выпуклость (convexity)
Если мы продолжим считать изменение цены облигаций в зависимости от изменения требуемой доходности, то обнаружим, что эта зависимость нелинейная (обычно, выпукла – цена чуть быстрее растет при снижении ставок и чуть медленнее снижается при их росте - см. на рисунке ниже).
Причина – разные ставки дисконтирования, которые мы используем для наших денежных потоков, когда доходность растет или падает. Поэтому положительные и отрицательные изменения доходности одной и той же величины по-разному влияют на цену, что приводит к выпуклому соотношению цена/доходность. Этот эффект и измеряет показатель выпуклости.
Можно сказать, что это нелинейное уточнение линейной дюрации (более точно – вторая производная от зависимости цена/доходность, дюрация – первая). Выпуклость становиться очень важной для оценки изменений цены облигаций при использовании длинных бумаг и больших изменениях в процентных ставках.
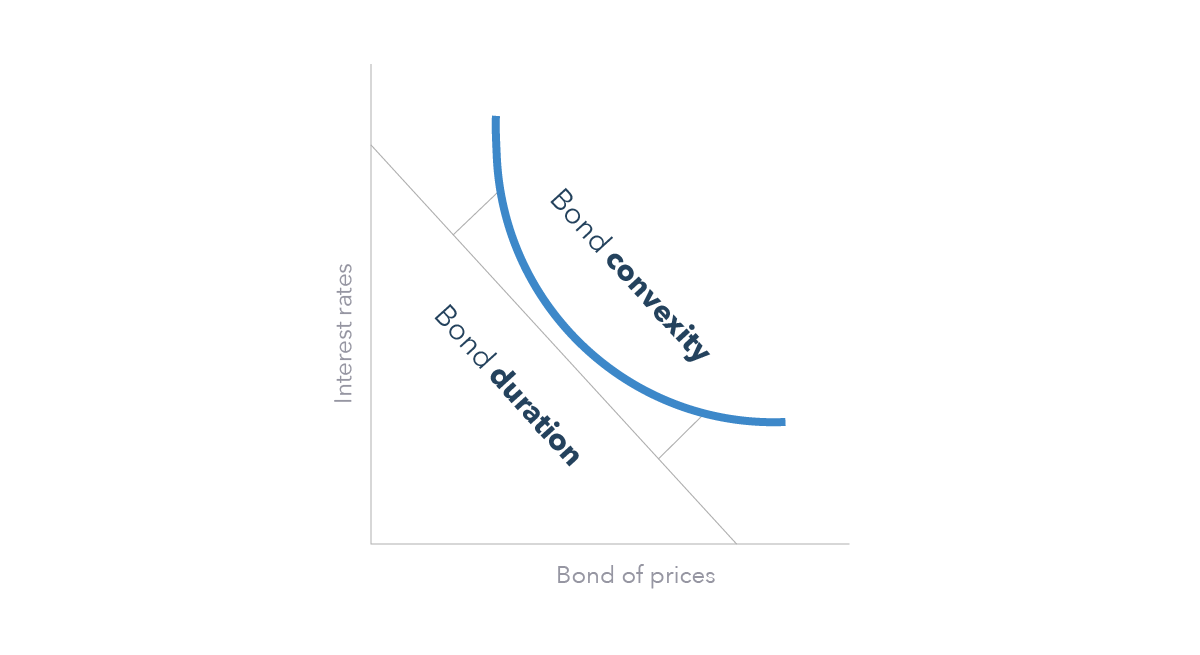
Дюрация (bond duration) измеряет линейную зависимость цены облигации от изменения процентных ставок, выпуклость (bond convexity) дополняет ее, чтобы точно отражать изменение цены при больших изменениях ставок
Здесь о Выпуклости можно почитать подробнее (Eng, pdf).
Как правило, более длинный срок погашения формирует более высокую выпуклость (причем она растет с сильным ускорением по мере роста срока). Чем больше выпуклость, тем больше цена облигации растет при снижении процентных ставок и медленнее падает при росте процентных ставок. Поэтому управляющие обычно стремятся, при прочих равных, максимизировать выпуклость портфеля.
В случае нашей задачки выпуклость Портфеля B, как правило, будет выше, чем у Портфеля A благодаря наличию относительно длинной облигации с дюрацией 5.5 лет.
Структура процентных ставок
Требуемые процентные ставки различаются для разных временных горизонтов (и дюрации). Как правило, они растут по мере роста такого горизонта – это нормальная форма кривой (или структуры) процентных ставок.
Увеличение наклона для нормальной формы кривой происходит, если краткосрочные ставки падают быстрее или растут медленнее долгосрочных.
Уменьшение наклона – краткосрочные ставки падают медленнее или растут быстрее долгосрочных. Обычно, ставки на всех горизонтах снижаются или растут, но сила этих движений может быть очень разной – если она примерно одинакова, то наклон кривой не изменяется (параллельное смещение).
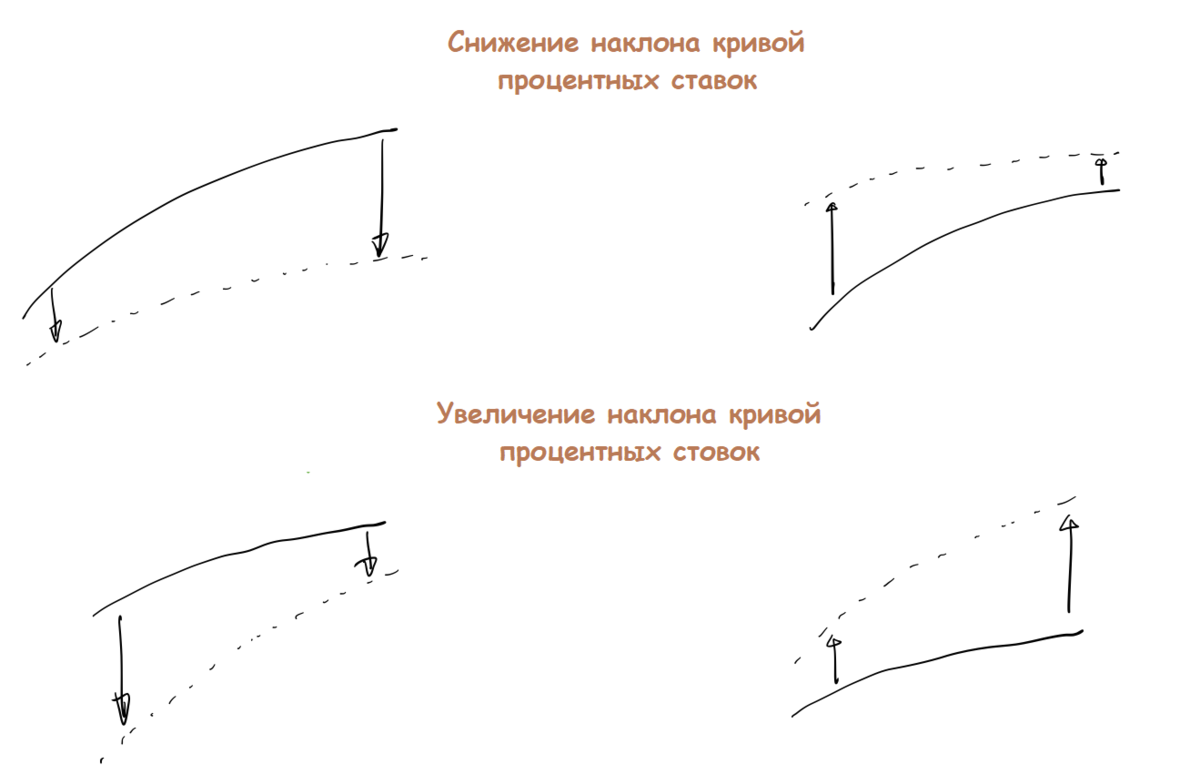
Изменения наклона кривой процентных ставок
В случае нашей задачки происходит уменьшение наклона кривой ставок (краткосрочные ставки растут быстрее долгосрочных). Для примера предположим, что для облигации с дюрацией 0.5 года требуемая доходность выросла на 2%, для средней облигации (с дюрацией 3 года) – на 1.5% и для относительно длинных бумаг (с дюрацией 5.5 лет) - на 1%.
Портфель облигаций
Как мы уже обсудили выше, цена каждой облигации будет изменяться по-разному в зависимости от дюрации бумаги, ее выпуклости и изменения требуемой доходности для данной дюрации.
Самые короткие облигации (дюрация 0.5 года) имеют очень низкую дюрацию (а значит, чувствительность к изменению ставок) и выпуклость (почти нулевую - не влияет на изменение стоимости коротких бумаг). Их цена из-за опережающего роста краткосрочных ставок, хотя и снизиться, но незначительно по сравнению с более длинными облигациями. Давайте предположим, что MD здесь тоже равен 0.5, и тогда изменение требуемой ставки на 2%, приведет к снижению цены примерно на 1% (=2%*0.5).
Бумаги с дюрацией 5.5 лет испытают самое большое отрицательное влияние роста ставок на цену, но так как имеют относительно большую выпуклость, этот эффект будет несколько смягчен. Если использовать только дюрацию MD=5 (снова сделаем такое предположение), то цена этой бумаги при росте требуемой ставки на 1% снизится примерно на 5.5% (=1%*5.5).
Так как растут и краткосрочные и долгосрочные ставки, разумно предположить, что среднесрочные ставки (в нашем случае для облигаций с дюрацией 3 года) тоже вырастут. Этот рост может быть разным, но обычно, это что-то среднее между изменениями в ставках на ближайшие соседние сроки. Снова предположим, что MD=3 и тогда при росте требуемой ставки на 1.5%, цена этой облигации снизиться на 4.5% (=1.5%*3).
Практически при любом подобном изменении кривой процентных ставок стоимость Портфеля B снизится меньше, чем стоимость Портфеля A.
Поэтому правильный ответ на нашу задачку: Портфель B покажет результат лучше.
Активные стратегии
Портфель B представляет стратегию Barbell («гантеля» - покупка коротких и длинных бумаг, без среднесрочных). Она, как правило, показывает более высокий результат, чем другие стратегии при данной целевой дюрации (риске) именно для ситуации, когда кривая процентных ставок снижает свой наклон.
В противовес ей, Портфель A реализует стратегию Bullet («пуля») и концентрирует вложения в облигации, имеющие целевую дюрацию (например, 3 года). Эта стратегия, как правило, покажет более высокий результат, если кривая процентных ставок увеличит свой наклон.
Если кривая ставок смещается параллельно, то, при прочих равных, Нейтральная стратегия (или «Лестница облигаций» - мы писали о ней здесь и она нацелена на равномерное распределение облигаций по срокам) будет лучшим выбором. Можно также отметить, что эта стратегия - наиболее проста и универсальна для большинства портфелей долгосрочных инвестиций.
Большинству инвесторов не обязательно строить сложные стратегии, но необходимо хорошо понимать, с какими рисками они сталкиваются при инвестировании в облигации (особенно долгосрочные) и фонды облигаций (которые нельзя держать до погашения и которые всегда подвержены риску изменения ставок).
Дюрация (особенно дюрация) и выпуклость в этом смысле – очень полезные показатели. Ищите их, когда оцениваете облигации и фонды облигаций для своих инвестиций.
=======
А если вам не подходят отдельные облигации, наш фонд BOND ETF может быть хорошим выбором для инвестирования в широкий портфель облигаций при минимальных затратах (всего 0.4% в год).
Полезные ресурсы:
Файл Excel c хорошим калькулятором дюрации, выпуклости и влияния изменения процентных ставок на цену облигации
Калькулятор на сайте МосБиржи (доходности, дюрации, выпуклости и пр.)
Файл Excel с примером построения "Лестницы облигаций"
Подробнее о выпуклости (Eng, pdf)
Портфель A: облигация с дюрацией 3 года. Портфель B: 50/50% две облигации с дюрацией 0.5 и 5.5 лет соотв. Доходности портфелей к погашению равны.
Какой портфель, скорее, покажет себя лучше если краткосрочные % ставки вырастут больше, чем долгосрочные?
Какой портфель, скорее, покажет себя лучше если краткосрочные % ставки вырастут больше, чем долгосрочные?
Голосование по ответам на задачку в нашем канале в Telegram @dohod
Из условий задачи видно, что она не требует точных расчетов. Изменение стоимости портфелей A и B, конечно, зависит от множества параметров: величины купонов и частоты их выплат для каждой облигации, точного срока погашения, текущей формы кривой процентных ставок, кредитного качества, кредитных спредов и т.д.
Здесь нам необходимо логически оценить наиболее вероятное влияние изменений процентных ставок на цену облигаций (процентный риск) и портфелей в целом, используя соответствующие параметры (дюрацию и выпуклость).
Если вы держите облигации до погашения, то у вас нет никакого риска процентных ставок. Если эмитент не подведет, то вы получите все купонные платежи и сумму номинала при погашении независимо от изменения рыночных процентных ставок. Но если деньги могут понадобиться вам раньше, то этот риск для вас актуален.
Дюрация (duration)
Справедливая цена облигации в любой момент времени равна сумме дисконтированных денежных потоков, которая она генерирует (купонов и сумм погашения). Зная цену облигации, легко (относительно) рассчитать ее доходность к погашению.
Если мы рассчитаем доходность облигации при падении ее цены на X рублей, то разница межу получившейся и начальной доходностью будет разной для разных облигаций (в основном из-за разницы в сроках до погашения и размерах купонов).
Значит, и наоборот, изменение на Y% доходности будет отражаться на разном изменении их цены. Чем больше такие изменения, тем больше чувствительность цены облигации к изменению процентных ставок (то есть, больше риск облигации). Именно это и отражает дюрация (D).
Дюрация, как и эффективная доходность к погашению (YTM) позволяет сравнивать друг с другом облигации, имеющие различные характеристики (срок, размер купонов, периодичность выплат и пр.). Классическая дюрация (дюрация Маколея) – это срок (в днях или годах), когда вложения в облигацию окупятся (но лучше воспринимать его как риск, описанный выше).
Дюрация - как точка опоры, уравновешивающая все дисконтированные платежи по облигации.
Представьте себе клюшку для гольфа. Ее длинна – это срок облигации до погашения. На протяжении всего этого срока вам обычно выплачиваются равные купоны – ручка клюшки прямая и ровная. Наконечник клюшки, однако, массивный и тяжелый – это финальный купон и сумма номинала, выплачиваемая при погашении облигации. Дюрация – это точка опоры такой клюшки, уравновешивающая все дисконтированные платежи по облигации. Чем меньше сама клюшка и чем дальше эта точка опоры от наконечника (даты погашения), тем быстрее окупится облигация, а заначит ее процентный риск ниже.
Очевидно, что чем больше срок до погашения облигации, тем выше ее риск, связанный с изменением процентных ставок. Длинные облигации (10,20 лет и более) имеют такой высокий риск, что часто ведут себя как акции с точки зрения волатильности (изменения цен).
В случае нашей задачки дюрация Портфеля A и Портфеля B одинакова и составляет 3 года (для Портфеля B = 0.5*50% + 5.5*50%). То есть, несмотря на то, что Портфель B состоит из двух облигаций с дюрациями 0.5 и 5.5 лет, он подвержен влиянию изменения процентных ставок в той же степени, что и Портфель A (на самом деле, не совсем - об этом ниже).
Модифицированная дюрация (MD), рассчитывается как D/(1+доходность) и измеряет примерное относительное (в %) изменение цены облигации при изменении процентной ставки на 1% годовых (100 базисных пунктов).
При MD=3 (для портфелей в задачке MD будет немного ниже, но одинаковой, так как портфели имеют одинаковую доходность) и росте требуемой доходности на 1%, цена облигации упадет примерно на 3%. Если доходность вырастет на 5%, то цена облигации упадет уже примерно на 15% (=5%*3). Как видим, здесь имеет место линейная зависимость.
Выпуклость (convexity)
Если мы продолжим считать изменение цены облигаций в зависимости от изменения требуемой доходности, то обнаружим, что эта зависимость нелинейная (обычно, выпукла – цена чуть быстрее растет при снижении ставок и чуть медленнее снижается при их росте - см. на рисунке ниже).
Причина – разные ставки дисконтирования, которые мы используем для наших денежных потоков, когда доходность растет или падает. Поэтому положительные и отрицательные изменения доходности одной и той же величины по-разному влияют на цену, что приводит к выпуклому соотношению цена/доходность. Этот эффект и измеряет показатель выпуклости.
Можно сказать, что это нелинейное уточнение линейной дюрации (более точно – вторая производная от зависимости цена/доходность, дюрация – первая). Выпуклость становиться очень важной для оценки изменений цены облигаций при использовании длинных бумаг и больших изменениях в процентных ставках.
Дюрация (bond duration) измеряет линейную зависимость цены облигации от изменения процентных ставок, выпуклость (bond convexity) дополняет ее, чтобы точно отражать изменение цены при больших изменениях ставок
Здесь о Выпуклости можно почитать подробнее (Eng, pdf).
Как правило, более длинный срок погашения формирует более высокую выпуклость (причем она растет с сильным ускорением по мере роста срока). Чем больше выпуклость, тем больше цена облигации растет при снижении процентных ставок и медленнее падает при росте процентных ставок. Поэтому управляющие обычно стремятся, при прочих равных, максимизировать выпуклость портфеля.
В случае нашей задачки выпуклость Портфеля B, как правило, будет выше, чем у Портфеля A благодаря наличию относительно длинной облигации с дюрацией 5.5 лет.
Структура процентных ставок
Требуемые процентные ставки различаются для разных временных горизонтов (и дюрации). Как правило, они растут по мере роста такого горизонта – это нормальная форма кривой (или структуры) процентных ставок.
Структура ставок может изменяться как угодно - краткосрочные ставки могу превышать долгосрочные, все ставки могут быть примерно на одном уровне и т.п. Даже при нормальной форме кривой может произойти увеличение или уменьшение ее наклона.
Увеличение наклона для нормальной формы кривой происходит, если краткосрочные ставки падают быстрее или растут медленнее долгосрочных.
Уменьшение наклона – краткосрочные ставки падают медленнее или растут быстрее долгосрочных. Обычно, ставки на всех горизонтах снижаются или растут, но сила этих движений может быть очень разной – если она примерно одинакова, то наклон кривой не изменяется (параллельное смещение).
Изменения наклона кривой процентных ставок
В случае нашей задачки происходит уменьшение наклона кривой ставок (краткосрочные ставки растут быстрее долгосрочных). Для примера предположим, что для облигации с дюрацией 0.5 года требуемая доходность выросла на 2%, для средней облигации (с дюрацией 3 года) – на 1.5% и для относительно длинных бумаг (с дюрацией 5.5 лет) - на 1%.
Портфель облигаций
Как мы уже обсудили выше, цена каждой облигации будет изменяться по-разному в зависимости от дюрации бумаги, ее выпуклости и изменения требуемой доходности для данной дюрации.
Самые короткие облигации (дюрация 0.5 года) имеют очень низкую дюрацию (а значит, чувствительность к изменению ставок) и выпуклость (почти нулевую - не влияет на изменение стоимости коротких бумаг). Их цена из-за опережающего роста краткосрочных ставок, хотя и снизиться, но незначительно по сравнению с более длинными облигациями. Давайте предположим, что MD здесь тоже равен 0.5, и тогда изменение требуемой ставки на 2%, приведет к снижению цены примерно на 1% (=2%*0.5).
Бумаги с дюрацией 5.5 лет испытают самое большое отрицательное влияние роста ставок на цену, но так как имеют относительно большую выпуклость, этот эффект будет несколько смягчен. Если использовать только дюрацию MD=5 (снова сделаем такое предположение), то цена этой бумаги при росте требуемой ставки на 1% снизится примерно на 5.5% (=1%*5.5).
В этом случае Портфель B потеряет около 3.25% (= 1%*0.5 + 5.5%*0.5), а в действительности немного меньше, благодаря действию более высокой выпуклости длинных облигаций.
Так как растут и краткосрочные и долгосрочные ставки, разумно предположить, что среднесрочные ставки (в нашем случае для облигаций с дюрацией 3 года) тоже вырастут. Этот рост может быть разным, но обычно, это что-то среднее между изменениями в ставках на ближайшие соседние сроки. Снова предположим, что MD=3 и тогда при росте требуемой ставки на 1.5%, цена этой облигации снизиться на 4.5% (=1.5%*3).
То есть Портфель A потеряет примерно 4.5% (немного меньше благодаря выпуклости, которая, однако, будет меньше, чем у Портфеля B).
Практически при любом подобном изменении кривой процентных ставок стоимость Портфеля B снизится меньше, чем стоимость Портфеля A.
Поэтому правильный ответ на нашу задачку: Портфель B покажет результат лучше.
Активные стратегии
Портфель B представляет стратегию Barbell («гантеля» - покупка коротких и длинных бумаг, без среднесрочных). Она, как правило, показывает более высокий результат, чем другие стратегии при данной целевой дюрации (риске) именно для ситуации, когда кривая процентных ставок снижает свой наклон.
В противовес ей, Портфель A реализует стратегию Bullet («пуля») и концентрирует вложения в облигации, имеющие целевую дюрацию (например, 3 года). Эта стратегия, как правило, покажет более высокий результат, если кривая процентных ставок увеличит свой наклон.
Если кривая ставок смещается параллельно, то, при прочих равных, Нейтральная стратегия (или «Лестница облигаций» - мы писали о ней здесь и она нацелена на равномерное распределение облигаций по срокам) будет лучшим выбором. Можно также отметить, что эта стратегия - наиболее проста и универсальна для большинства портфелей долгосрочных инвестиций.
Все это активные стратегии, направленные на выбор структуры дюрации вашего портфеля в зависимости от вашего прогноза изменения структуры процентных ставок. Как и любые активные стратегии – они сложны в реализации и поддержании в рабочем состоянии.
Большинству инвесторов не обязательно строить сложные стратегии, но необходимо хорошо понимать, с какими рисками они сталкиваются при инвестировании в облигации (особенно долгосрочные) и фонды облигаций (которые нельзя держать до погашения и которые всегда подвержены риску изменения ставок).
Дюрация (особенно дюрация) и выпуклость в этом смысле – очень полезные показатели. Ищите их, когда оцениваете облигации и фонды облигаций для своих инвестиций.
=======
А если вам не подходят отдельные облигации, наш фонд BOND ETF может быть хорошим выбором для инвестирования в широкий портфель облигаций при минимальных затратах (всего 0.4% в год).
Полезные ресурсы:
Файл Excel c хорошим калькулятором дюрации, выпуклости и влияния изменения процентных ставок на цену облигации
Калькулятор на сайте МосБиржи (доходности, дюрации, выпуклости и пр.)
Файл Excel с примером построения "Лестницы облигаций"
Подробнее о выпуклости (Eng, pdf)
Не является индивидуальной инвестиционной рекомендацией | При копировании ссылка обязательна | Нашли ошибку - выделить и нажать Ctrl+Enter | Жалоба

