18 ноября 2014 ray-idaho.ru ray_idaho
Население и приблизительное распределение населения по доходам крупных стран в миреРанее я давал методику расчета коэффициента Джини, оценивающее уровень неравенства в обществе.
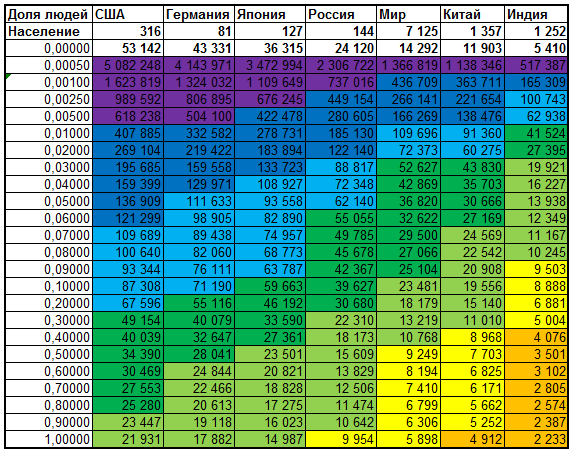
В таблице приведено распределение доходов по группам по мере падения доходов по 6 странам из прошлого текста. Цвета идут от фиолетового (доходы свыше 500 тыс.$ в год) к синему (от 500 тыс.$ до 120 тыс.$), далее голубому (от 120 тыс.$ до 60 тыс.$), затем зеленый (от 60 тыс.$ до 25 тыс.$), к светло-зеленому (от 25 тыс.$ до 10 тыс.$), к желтому (от 10 тыс.$ до 5 тыс.$) до светло-коричневого (менее 5 тыс.$). Сами группы идут сначала по 10%, потом по 1% и в конце убывает каждая следующая примерно в 2 раза.
Во второй строке таблице приведено население стран в миллионах, потом ВВП по ППС на душу на 2012 год. За счет неравенства даже в бедной Индии людей с доходами выше 500 тыс.$ в год (с учетом ППС) около 500 тыс. человек. В среднем же по миру их несколько миллионов человек, в номинальных долларах их поменьше. Например, по мнению сайта Globalrichlist - их всего 1,1 миллион человек.
Неоднородность общества - коэффициент Джини
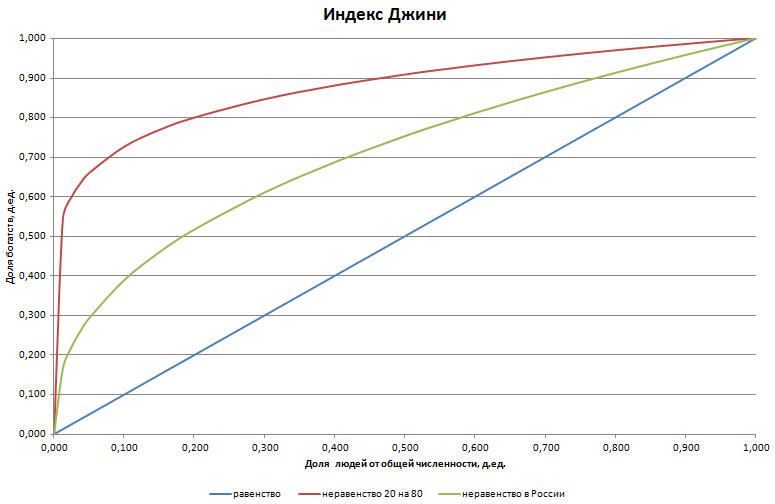
Часто используемым показателем неоднородности является коэффициент Джини, который вычисляется с помощью кривой Лоренца (пример кривых на рисунке). Для простоты вычисления можно взять функцию для кривой Лоренца в виде степенной зависимости, нередко появляющейся при анализе фрактально-построенных физических или социальных объектов, например, функция распределения вероятности Ципфа.
Пусть кривая Лоренца описывается функцией вида:
L(x)=xa, где a - число меньшее 1.
В этом случае значение коэффициента Джини будет следующим:
Джини(a) = (1/(1+a)-1/2)*2
На рисунке можно увидеть 3 различных кривых Лоренца
- первая соответствует полному равенству, в этом случае a=1
- вторая соответствует неравенству в России, в этом случае a=0,41, а коэффициент Джини=0,42
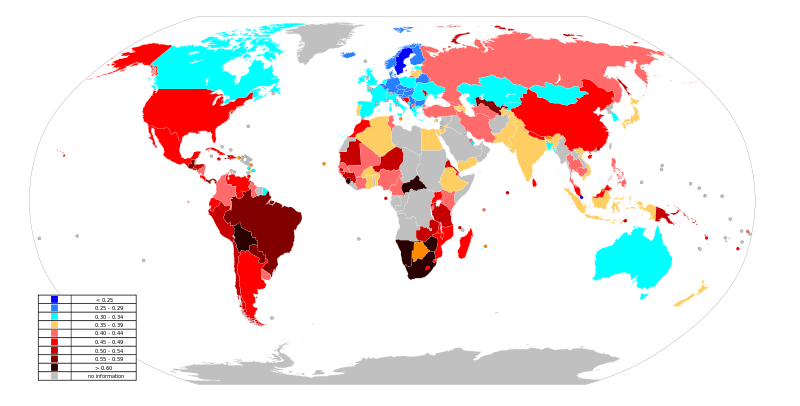
- третья соответствует неравенству по принципу Парето (20 на 80), в этом случае a=0,139, а коэффициент Джини=0,76 (такой коэффициент не встречается в существующих государствах - второй рисунок)
График кривой Лоренца
Карта коэффициента Джини
http://www.ray-idaho.ru/blog/ (C) Источник
Не является индивидуальной инвестиционной рекомендацией
При копировании ссылка обязательна Нашли ошибку: выделить и нажать Ctrl+Enter