28 августа 2015 QuantAlgos
Введение
Стратегия, основанная на рыночно-нейтральном подходе, подразумевает, что трейдер должен принять три основные решения:
Выбрать активы для торговли из набора множества торгуемых инструментов
При существующем спреде ( т.е. динамически взвешенной разнице между двумя активами) определить его смысл в соответствующих эконометрических терминах
Выбрать торговый алгоритм
Если стратегия оперирует только одним активом, первая задача тривиальна, вторая исчезает и только третья остается действительно важной. В другом случае, при парном трейдинге, все задачи одинаково важны.
Механизм статистического арбитража глубоко связан с концепцией баланса двух цен. Когда такой баланс нарушен, возникает возможность извлечения прибыли, при условии, что отношение баланса будет рано или поздно восстановлено. Такие модели страдают от трех видов рыночного поведения, которые могут быть описаны как:
Спред не сходится в дальнейшем: система никогда не будет прибыльной
Баланс восстанавливается медленно: некоторые стратегии могут закрыть позиции перед схождением спреда
Волатильность спреда возрастает: стратегия может перестать быть прибыльной, так как порог для сигнала входа в позицию преодолевается слишком рано и разница между двумя ценами расходится в ближайшем будущем.
Цель модели, предлагаемой в данной статье - избежать негативных последствий, связанных с ростом волатильности, с попыткой получить дополнительную прибыль от него. Традиционные алгоритмы предписывают покупать (продавать) спред, когда цена выйдет за порог нижней (верхней) линии диапазона Боллинджера: мы предлагаем создать другие входные сигналы, согласованные с текущим режимом волатильности, найденные с помощью определения порогов, характеризующих данный режим. Мы исследуем два подхода к определению порогов: первый использует гауссовскую смесь двух распределений, второй использует марковскую модель скрытых состояний (НММ), для учета возможного присутствия некоторой временной зависимости.
Производительность этих подходов измерена на бэктестировании, результаты которого довольно хороши, так как стратегия показала большие доходность и коэффициент Шарпа, по отношению к обычным алгоритмам парного трейдинга.
Система тестировалась на 10 и 20 минутных ценах закрытия семи фьючерсных пар с октября 2012 года по сентябрь 2014 года. Две пары взяты из энергетического сектора - межрыночный спред между фьючерсом на нефть Лайт Свит (CL) и фьючерсом на нефть Брент (BRN), и сырьевая пара из мазута (HO) и бензина RBOB (RB). Из сельскохозяйственного сектора взяты пары фьючерсов на соевую муку (ZM) и соевое масло (ZL), а также на сою (ZS) и кукурузу (ZC). Последние три спреда созданы из мини фьючерсов на индекс Доу-Джонса (YM) , Nasdaq (NQ) и SnP 500 (ES).
Обзор литературы
Выбор активов
Критерий минимального расстояния - это простой и интуитивно понятный метод, предложенный E. Gatev, W. N. Goetzmann, and K. G. Rouwenhorst. Pairs trading: Performance of a relative-value arbitrage rule. Review of Financial Studies, 19:797–827, 2006. Корреляционный фильтр позволяет нам найти порог и торговать парми, чья корреляция его превышает. Коинтеграционные фильтры (A. G. Modi, J. Desai, Dave A. R., and K. J. Desai. Finding the identical twin.Econometrics: Multiple Equation Models eJournal, 2011) были созданы в качестве альтернативы корреляции с целью нахождения долгосрочного взаимоотношения между двумя временными сериями. Значимость беты - другой простой инструмент, основанной на значимости коэфиициента регрессии бета между двумя временными сериями. Методы ETF, впервые предложенные M. Avellaneda and J. H. Lee. Statistical arbitrage in the US equities market. Quantitative Finance, 2010, выведены из хоошо известной концепции общих факторов риска. Здесь используются активы биржевых фондов - корзин активов с общими рыночными факторами, как инструменты хэджирования. В этой же статье также предлагается процедура, основанная на анализе принципиальных компонентов (метод машинного обучения) для выбора наилучших компонентов для целей торговли.
Моделирование спреда
Коэффициент минимальной дисперсии - это хорошо известная техника хэджирования ( например, J. C. Hull. Options, Futures, And Other Derivatives. Pearson, 8th edition, 2012), где коэффициент бета используется для взвешивания двух активов таким образом, что результирующая дисперсия портфеля минимизируется.
Обобщенный метод наименьших квадратов TLS (P. Teetor. Better hedge ratios for spread trading. Unpublished note, 2011. URL http://quanttrader.info/public/) использует тот факт, что для целей парного трейдинга, операции покупки одного актива и продажи другого или наоборот, не должны различаться. В случае классического метода наименьших квадратов (OLS) принимается во внимание дисперсия только одного актива из спреда - это приводит к ассиметричному учету рыночных факторов. С другой сторны, коэффициент хэджирования, найденный с помощью TLS согласован с рынком и дисперсия учитывается симметрично.
Другая возможность состоит в моделировании спреда как авторегрессивного процесса первого порядка. A. N. Burgess. A Computational Methodology for Modelling the Dynamics of Statistical Arbitrage. PhD thesis, London Business School, 1999 использует дискретный процесс, в то время, как W. K. Bertram. A non-stationary model for statistical arbitrage trading. SSRN,http://ssrn.com/abstract=1632718, 2010 применяет непрерывный подход.
Реже спред описывается моделью скрытых состояний Маркова. Первая версия была представлена в R. Bock and M. Mestel. A regime-switching relative value arbitrage rule. Operations Research Proceedings, 2008: согласно авторам, временной ряд спреда содержит структурные разрывы и предположение о постоянных параметрах становится неверным. Структурные разрывы в экономических и финансовых временных сериях возникают в результате финансовых кризисов, войн, политических изменений или пузырей в сырьевых активах, и могут влиять на параметры авторегрессии, коэффициенты регресии, средние значения, дисперсию или на параметры модели GARCH. Авторы статьи создают модель, где переключения режимов управляются марковскими цепями, текущий режим определяется ненаблюдаемой переменной и основан на вероятности состояний. Формально, модель является процессом Маркова первого порядка с двумя состояниями, с переключающимися средним значением и дисперсией.
В статье A. Bucca and M. Cummins. Synthetic floating crude oil storage and optimal statistical arbitrage: A model specification analysis. SSRN, http://ssrn.com/abstract=1932432, 2011 вместо структурных разрывов анализируется коинтеграционные взаимоотношения между различными временными сериями. Описано, как коинтеграционная модель может иметь непостоянные параметры и может являться процессом с переключением среднего значения или трендовым процессом с переключением среднего, либо процессом с двумя режимами.
Иногда спред моделируется с использованием динамического процесса с латентной переменной, чьи параметры устанавливаются с помощью фильтра Калмана. Например, в E. P. Chan. Algorithmic Trading - Winning Strategies and Their Rationale. Wiley,2013 предлагается модель, которая рекурсивно вычисляет коэффициент регрессии, избегая дискретных решений или произвольного выбора.
В заключении, спред может быть описан в соответствии с физическими отношениями, исходящими из эмпирических свидетельств, основанных больше на экономических причинах. чем на математических моделях. Типичные примеры спредов на обвалах рынка рассмотрены в J. B. Mitchell. Soybean futures crush spread arbitrage: Trading strategies and market efficiency. Journal of Risk and Financial Management, 2010.
Выбор торгового алгоритма
Для торгового алгоритма простейшее решение - это гипотеза белого шума для спреда, которая предполагает, что спред является белым шумом. Некоторые применения оптимизируют коэффициент при дисперсии в диапазонах Боллинджера, другие (E. Gatev, W. N. Goetzmann, and K. G. Rouwenhorst. Pairs trading: Performance of a relative-value arbitrage rule. Review of Financial Studies, 19:797–827, 2006) устанавливают этот коэффициент равным 2, согласно 95% порговой величины нормального распределения.
Подобно приращениям, вычисленным из цен активов, в большинстве случаев эмпирические наблюдения говорят о том, что спред не следует нормальному распределению, соответственно, более сложный подход использует негауссовскую плотность распределения. Разные, возможно непараметрические, техники, могут быть созданы в порядке учета таких особенностей, например в G. Vidyamurthy. Pairs Trading - Quantitative Methods and Analysis. Wiley, 2004 используется альтернативный метод, основанный на смеси гауссовских распределений.
Моделирование скачков волатильности
Для определения, режим какой волатильности присутствует на рынке - высокой или низкой, могут быть применены различные инструменты. Общее допущение - спред является стационарным с ожидаемым значением, равным нулю. Для задачи моделирования всего распределения в данной статье мы используем два различных метода: первый, где спред определяется смесью двух гауссовских плотностей распределения; второй, где процесс генерации данных предполагается стохастическим процессом с переключением режимов волатильности. Последний метод является обобщением первого, где последовательность скрытых переменных генерирует набор зависимых наблюдений, следующих процессу Маркова, таким образом, возможные временные зависимости включены в модель. В следующих частях статьи, после определения понятия спреда, мы произведем глубокий анализ этих двух методов. При переходе к реальным данным, в обоих случаях гауссовской смеси и модели Маркова, мы будем, первое, определять два режима с идентичным ожидаемым средним значением, но разным стандартным отклонением, и, второе, плотность с более низкой дисперсией, ассоциируемой с бОльшим параметром вероятности.
Модель гауссовской смеси
Плотность распределения смеси двух наборов нормальных плотностей определяется следующим образом:
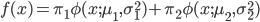, где
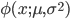- нормальная плотность распределения с параметрами и 
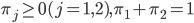, так что мы можем принять 
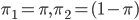. Тогда мы можем переписать формулу следующим образом: 
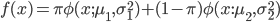. Вектор неизвестных параметров определим как
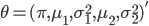, содержащий вероятность принадлежности к первому распределению 
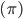, и ожидаемое значение и дисперсию обоих распределений вероятности. Модель Маркова
Вторая модель была предложена для целей парного трейдинга в статье R. Bock and M. Mestel. A regime-switching relative value arbitrage rule. Operations Research Proceedings, 2008. Но марковские модели использовались и намного раньше. Для их вычисления был создан алгоритм максимального правдоподобия на основе EM алгоритма, предложенный J. D. Hamilton. Analysis of time series subject to changes in regime. Journal of Econometrics, 45:39–70, 1990 . В предложенной модели режимы переключаются в зависимости от последовательностей Маркова. Режим определяется скрытыми переменными, и вывод о текущем режиме основан на вероятности состояний. Используемый здесь процесс имеет два режима, с переключающимися значениями средней и дисперсии. Хотя, в принципе, может быть неразумно иметь дело только с фиксированными средними значениями, данная модель с переключением производит лучшие оценки.
Основная разница между нашей моделью и моделью Bock и Mestel (2008) лежит в плоскости предмета моделирования. В то время, как у них определяемым значением является коэффициент хэджирования, наша временная серия - это сам спред, а не его компоненты. Формально, процесс определяется как
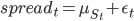, где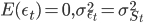 
. Отметим. что в определении модели Bock и Mestel переключения среднего значения были необходимостью. В нашем случае, при использовании модели для спреда, являющегося стационарным процессом, такой необходимости нет.
В следующей части мы определим устойчивую модель парного трейдинга для различных режимов волатильности и протестируем ее на реальных данных.
Модель, устойчивая к смене режимов волатильности
Некоторые проблемы торговли спредом
Ранее мы определили три сосотавляющих рыночно-нейтральных стратегий. Здесь мы обновим эту классификацию и рассмотрим некоторые трудности, связвнные с торговлей спредом.
Долговременные расхождения в ценах трудно найти с помощью алгоритмов, основанных только на ценах. Обычно, фундаментальный анализ, совместно с опытом трейдера может помочь в понимании существования расхождения. Время возврата к среднему может быть установлено с помощью непрерывных моделей, в этом случае период удержания позиции зависит от модели спреда и, следовательно, от частоты пересчета коэффициента хэджирования.
Много факторов могут приводить к скачкам волатильности спреда, но сами по себе скачки не могут быть приняты в качестве сигналов прекращения торговли парой.
При частом обновлении коэффициента хэджирования предпочтительней определять скачки в волатильности, чем в среднем значении. С другой стороны, если коэффициент меняется не так часто, переходы среднего значения также можно вычислять, так как спред начинает демонстрировать сильную зависимость от будущего отношения цен.
Стратегия тестирования из трех частей
1. Идентификация пары
В этой части мы применим некоторые понятия, представленные выше, в качестве фильтра включения/исключения актива для нашего алгоритма. Так как мы используем внутридневные данные, фильтры вычисляются с дневной частотой, то есть длина тренировочного и тестового набора состоят из 11 часов предыдущего дня.
Семь пар было выбрано с целью избежать ложной корреляции или случайных совпадений. Так как мы тестируем стратегии на сырьевых и индексных фьючерсах, мы не фокусируемся на фундаментальном анализе, он мог бы рекомендоваться при торговле акциями.
Мы применим три простых фильтра:
5% -й уровень значимости коэффициента наклона линейной регрессии;
корреляция между ценами более более 80%;
5% уровень значимости коинтеграционного отношения между ценами двух активов, по статье D. Kwiatkowski, P. C. B. Phillips, P. Schmidt, and Y. Shin. Testing the null hypothesis of stationarity against the alternative of a unit root. Journal of Econometrics, 54:159–178, 1992.
2. Моделирование спреда
Спред определяется как взвешенная разность между двумя ценами:
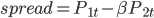
Частота выборки равна 10 или 20 минутам, и коэффициент хэджирования обновляется каждый день, используя данные предыдущего дня, путем метода усреднения коэффициента минимальной дисперсии (смотрите обзор литературы в предыдущей части). Частота обновления соответствует строго внутридневной модели торговли.
Этот выбор имеет преимущество в связи с избежанием начисления ночной маржи на открытую позицию, в то же время, позиция не удерживается более одного торгового дня, что является довольно жестким ограничением.
3. Торговый алгоритм
Торговая модель представляет собой обычную стратегию с возвратом к среднему, использующую диапазоны Боллинджера.Эта модель применяет четыре диапазона, самы широкий в качестве сигнала входа, а самый узкий - как сигнал выхода из позиции. Как следствие, стратегия не все время находится в рынке. Есть только один дополнительный сигнал выхода ( не являющийся взятием прибыли), соответствующий окончанию торгового дня.
Эта стратегия сравнивается с другой, которая использует порог волатильности для определения коэффициента при дисперсии (ширины полос Боллинджера) , лучше подходящий текущему состоянию волатильности. Таким образом, существует восемь диапазонов, четыре для низкой волатильности и четыре - для высокой.
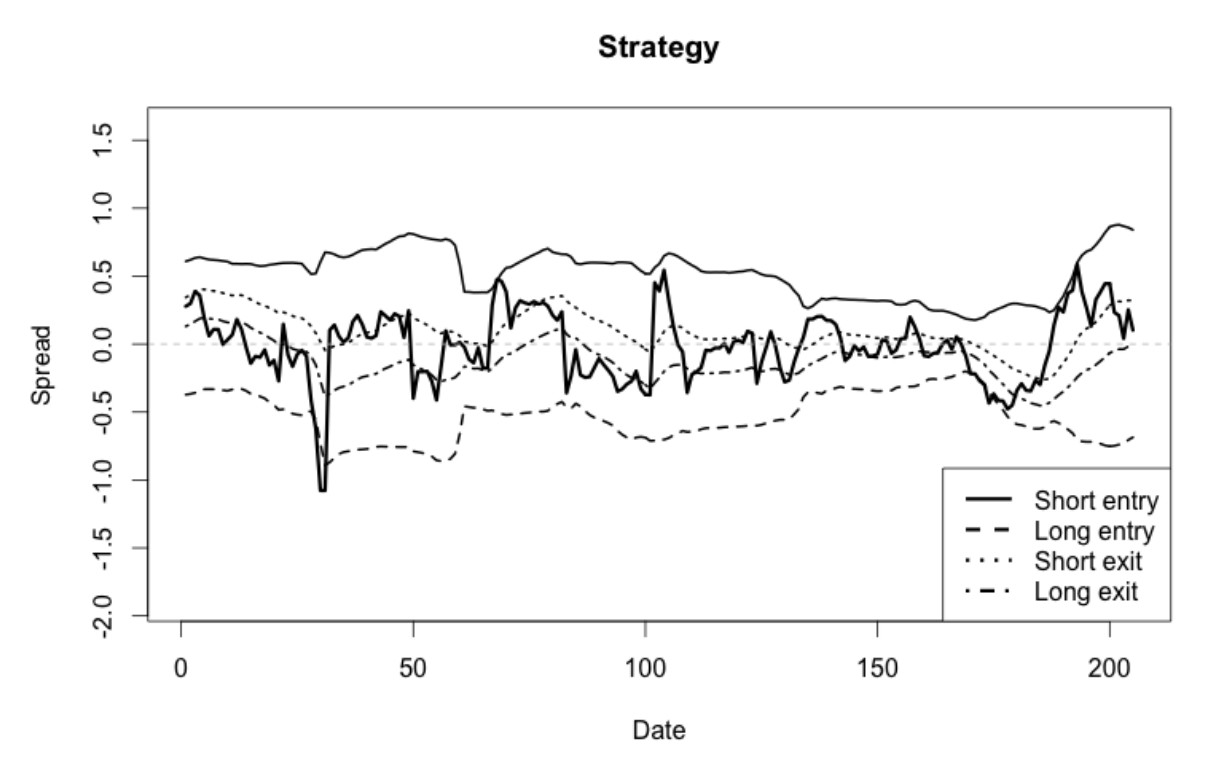
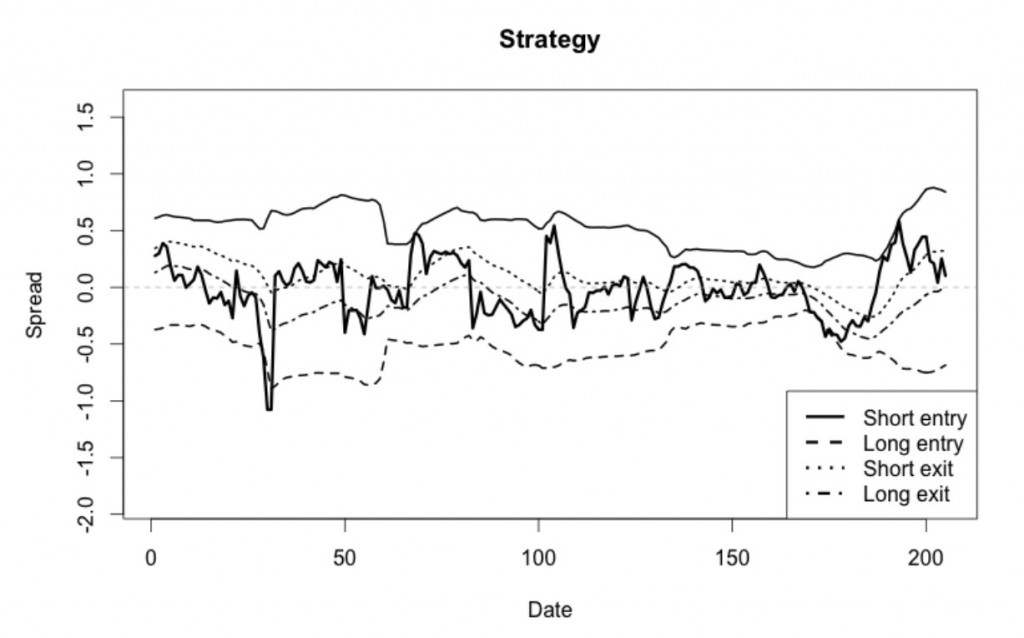
В качестве примера первая модель ( с 4 диапазонами) показана на рисунке ниже. Когда закрытие свечи выше сплошной линии, мы продаем актив, и наоборот, когда цена закрытия уходит под нижнию линию. Для узкого диапазона, соответственно, верхняя линия - выход из длинной позиции, а нижняя - выход из короткой. Так как мы ожидаем контртрендовое поведение спреда, то делаем ставку на внутридневной возврат к среднему.
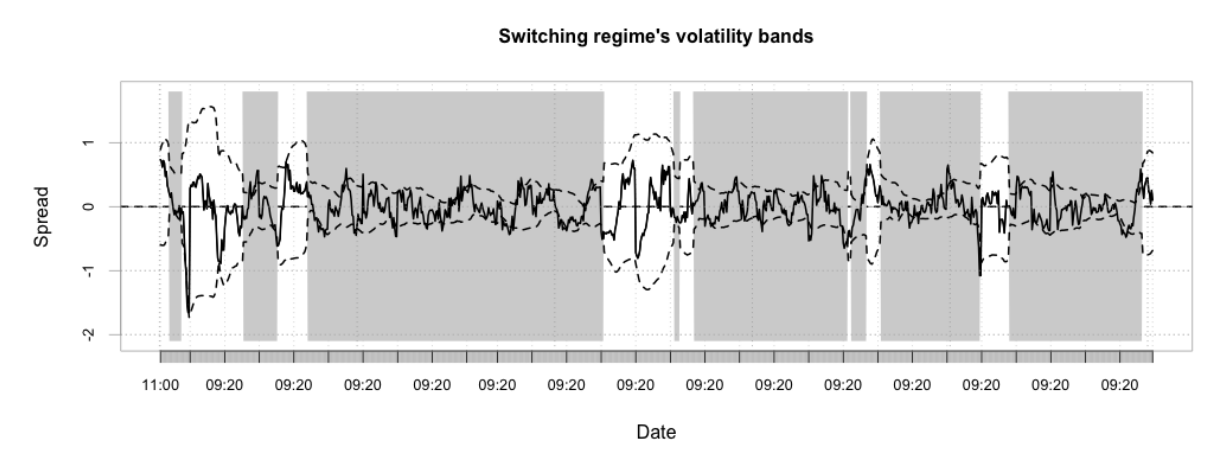
Следующая система основана на двух разных режимах. Инидикаторы разделены на три группы: уровни входа, уровни выхода и порог переключения режимов. Порог является различием между первой моделью и нашим подходом, и гауссовская смесь и НММ играют ключевую роль в его определении.
Так как порог указывает на уровень волатильности, соответствующий переходу от одного режима к другому, задача состоит в их правильном определении. Для гауссовской смеси мы используем, как порог, большее стандартное отклонение из двух, составляющих смесь, популяций. Также, для НММ мы применяем большее стандартное отклонение из двух моделей перехода.
Результаты
Мы разделили данные на четыре выборки, использовав первую и третью как тренировочные наборы. Также, мы установили порог равным средним значениям двух тренировочных наборов. Затем мы применили эти величины для тестирования стратегии с единым порогом для всех выборок.
Все вычисления производились на языке R. Конкретно, использовались библиотеки mixtools и MSwM, соответственно, для гауссовской смеси и модели Маркова. В обоих случаях максимальное правдободобие находилось с помощью ЕМ алгоритма. Так как размер выборки был приблизительно равен 4500, время вычислений достаточно мало, несколько секунд в случае гауссовской смеси и около минуты для НММ.
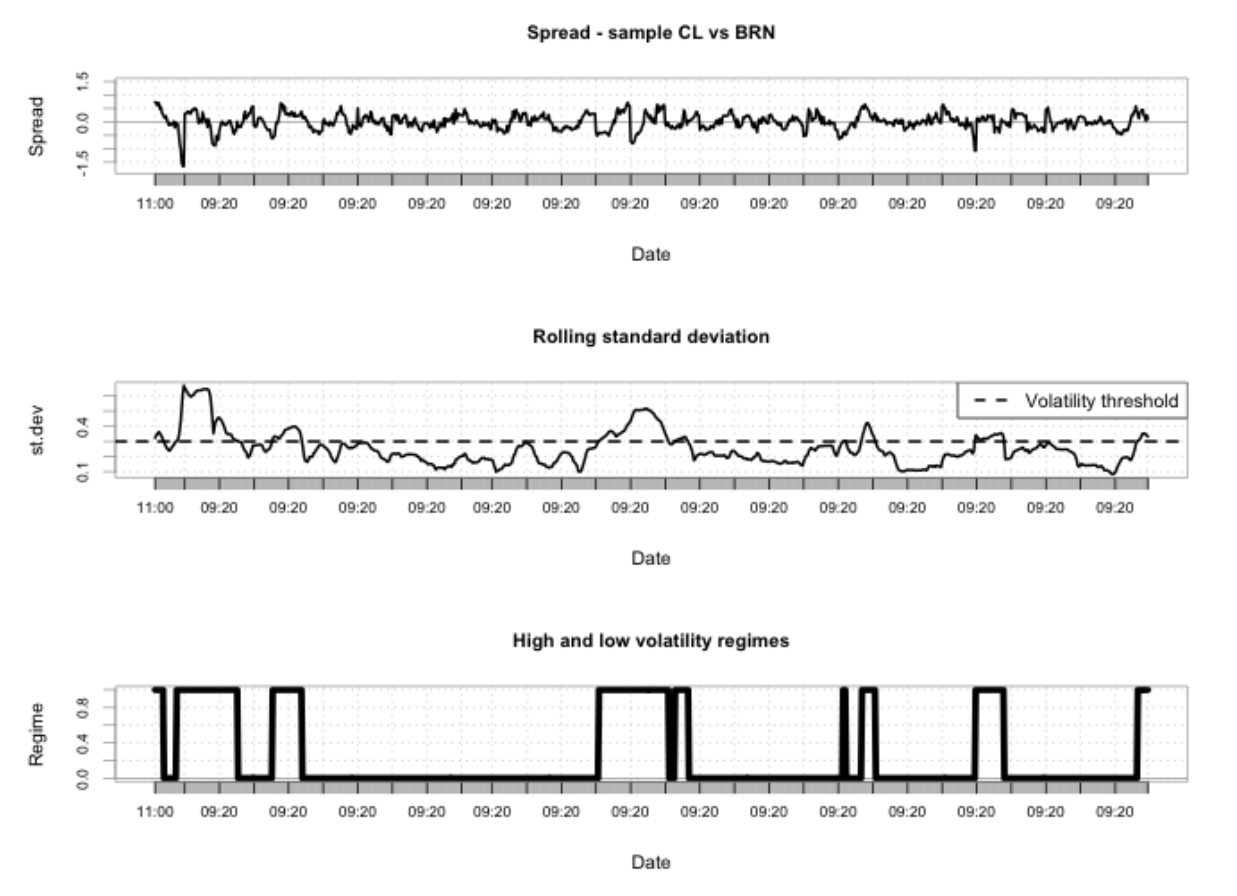
Три области на рисунке в заглавии статьи графически представляют, как определялись режимы. Верхняя панель показывает, что периоды высокой волатильности сменялись периодами низкой волатильности и такое поведение носило перманентный характер. Средняя панель показывает скользящее стандартное отклонение с порогом (прерывистая линия): режимы высокой волатильности соответствуют периодам, где стандартное отклонение выше линии, низковолатильные режимы соответствуют обратной ситуации. Нижняя панель отражает сами режимы. На рисунке ниже показано, как уровни входа изменяются соответственно с определенной волатильностью. Отметим, что выходы меняются подобным же образом.
В соответствии со смоделированным спредом, мы предполагаем покупать (продавать) пять контрактов по одному активу, одновременно продавая (покупая) количество, равное
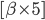, где [x] - целая часть х, по другому активу, так как число контрактов должно быть целым.Мы моделируем торговлю с 500 000$ и наше гарантийное обеспечение будет примерно равным 20%. Мы не используем какую-либо технику манименеджмента, ГО 20% будет только в начале периода бэктестинга и будет снижаться по мере получения прибыли.
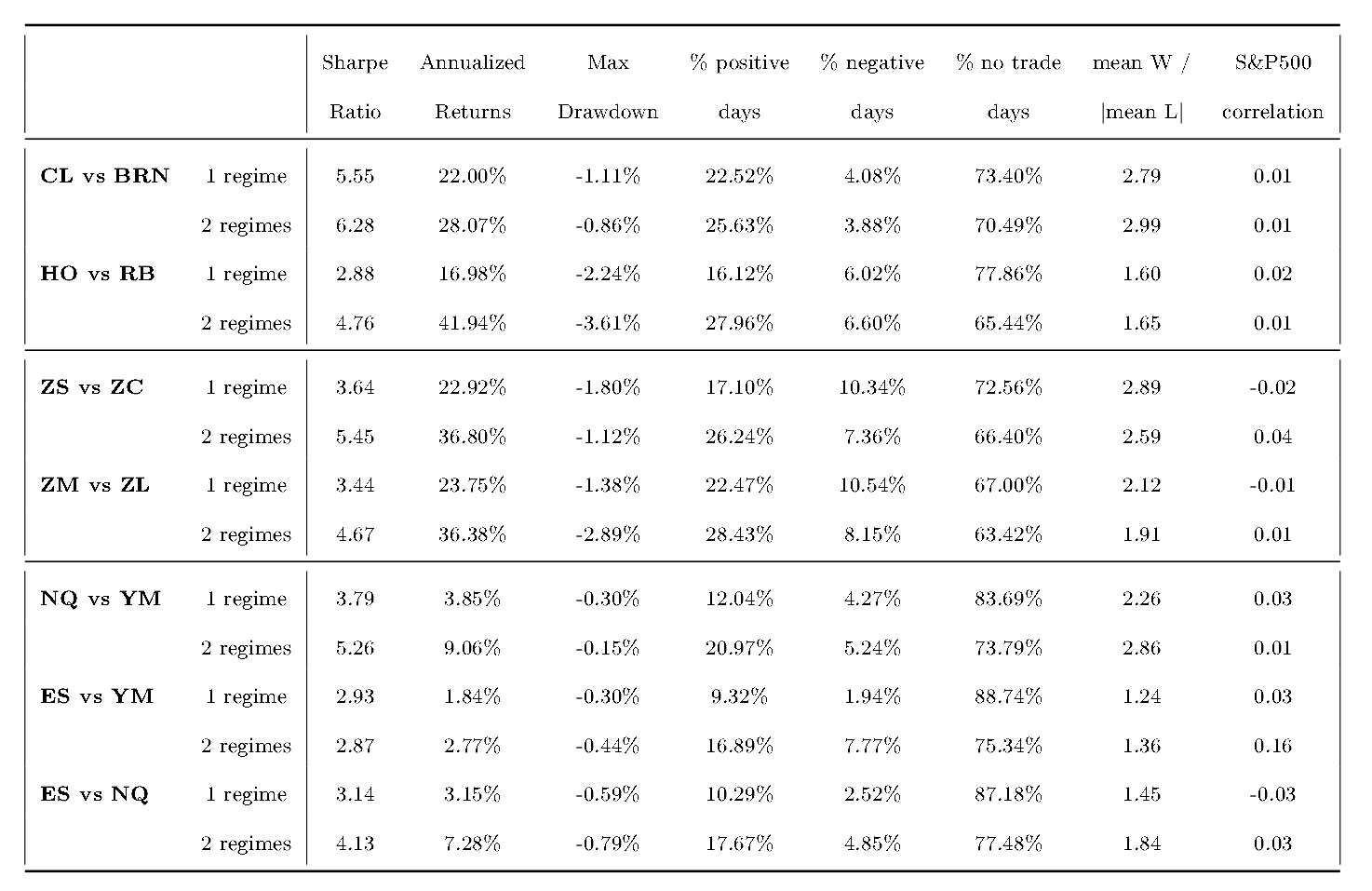
Итоговые результаты анализируются с помощью распространенных индикаторов, применяемых на практике: годовой коэффициент Шарпа, годовая доходность, максимальная просадка, доли дней с положительной и отрицательной доходностью, доля дней без сделок, коэффициент отношения среднего значения (в долларах) дней с положительной доходностью к дням с отрицательной доходностью, корреляция портфеля с индексом SnP500. Во всех случаях мы указываем чистый результат, принимая во внимание 3$ комиссии и один тик проскальзывания на сделку.
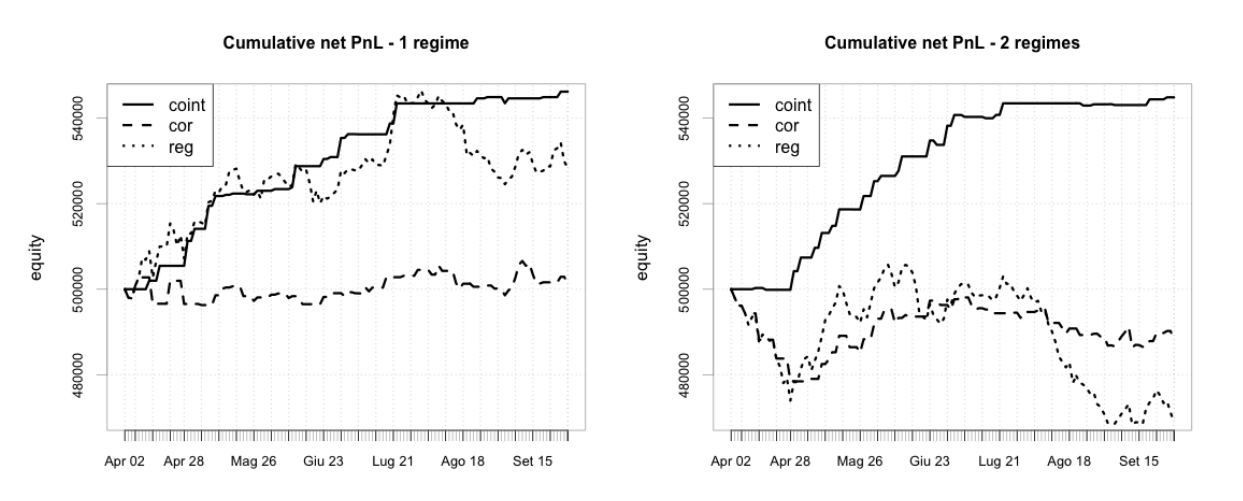
Наиболее существенный полученный нами вывод - это то, что коинтеграционный фильтр работает лучше, чем два остальных (см. предыдущую часть). Рисунок в заглавии показывает, как в течение последнего семестра, в начале падения нефтяных цен, только те стратегии дают удовлетворительный результат, которые построены на коинтеграции. С другой стороны, алгоритм показывает слабые результаты при использовании корреляции или значимости регрессии в качестве фильтров.
Одна из наиболее известных проблем внутридневных спредовых стратегий - влияние комиссий. В наших тестах 10 минутный таймфрейм сильнее подвержен такому влиянию, чем остальные.
В таблице ниже мы показываем результаты только 20 минутного периода с коинтеграционным фильтром, так как в 10 минутном периоде получены похожие значения. Исключая спред между контрактами ES и YM , все другие стратегии демонстрируют лучшую производительность с двумя режимами, чем с одним.
Более того. все методы показывают положительную доходность и большие коэффициенты Шарпа. Существует, тем не менее, серьезная разница между доходностями сырьевых активов и финансовых индексов; в то время как индексные фьючерсы ликвиднее, чем сырьевые, их доходности ниже. В обоих секторах коэффициенты Шарпа более 2, так что даже первая стратегия имеет хорошие результаты.
Общий риск определенно мал, так как величина просадок в таблице может быть с уверенностью поглощена без особых проблем. В среднем, процент отрицательной дневной доходности мал, но при вычислениях нужно учесть влияние коинтеграционного фильтра: доля дней без сделок лежит между 60 и 80%.
Другая важная особенность заключается в разности между числом неторговых дней с одним и двумя режимами: во втором случае сделок в среднем больше, чем в первом. Как следствие этого, число дней с положительной доходностью также увеличивается в некоторых случаях, где есть снижение коэффициента "средних выигрышей к средним проигрышам". Так как комиссия не сильно влияет на чистую прибыль, общая производительность получается стабильней.
По всем нашим протестированным вариантам, решения о применяемых фильтрах и параметрах в основном зависели от подверженности трейдеру риску " неправильной стороны" сделки (risk aversion). Как сказано выше, применение коинтеграционного фильтра приводит к меньшему числу сделок и менее волатильной доходности, и должен быть предпочтен остальным. В частности, число сделок лежит всегда между четырьмя и восемью в день и доля торговых дней в среднем равно 25%, таким образом число транзакций достаточно велико для получения устойчивого результата.
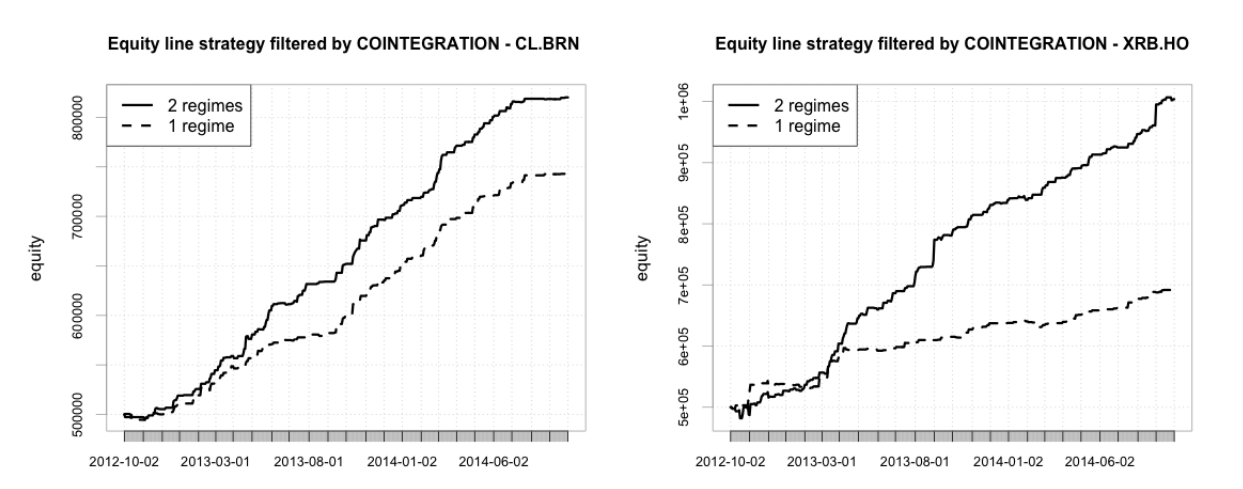
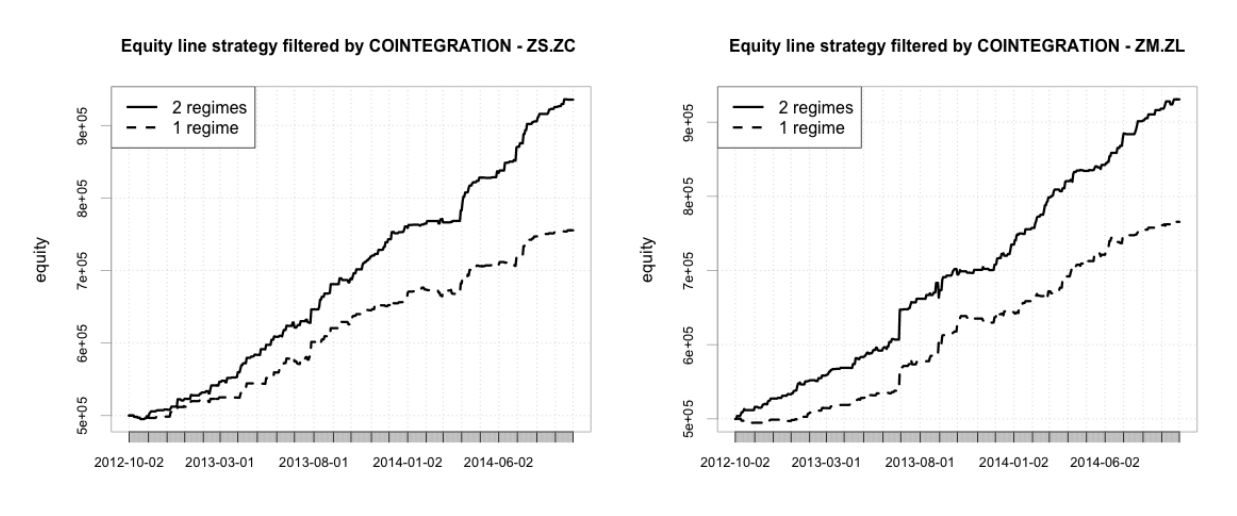
В итоге, отсутствие корреляции с индексом SnP500 - значимая характеристика как для институциональных, так и частных инвесторов, и вносит диверсификационный эффект в портфель. Доказательства преимуществ нашей стратегии следуют из графиков ниже, где показана линия эквити в сравнении с алгоритмом одного режима.
Заключение
В данной статье мы создали новую модель, демонстрирующую, как стратегии парного трейдинга работают на разных контрактах. Мы проанализировали два альтернативных способа определения режимов волатильности. Так как оценки похожи в обоих случаях, производительности стратегий также близки.
Предлагаемый метод имеет несколько преимуществ, но и некоторые недостатки. Производительность, получаемая с коинтеграционным фильтром устойчива по всем парам и временным периодам. Корреляция с классическим портфелем buy&hold приблизительно равна нулю, так что эти инвестиции интересны для всех трейдеров. Обе модели с одним и двумя режимами показывают низкую волатильность приращений, но последняя модель делает возможным увеличение доходности пропорционально с волатильностью.
Некоторые трудности могут возникнуть с практическим применением. Первое, может быть недостаток ликвидности на сырьевых рынках. Второе, масштабируемость -она также важна, и каждый трейдер должет принимать это во внимание. В итоге, мы не можем позволить себе использовать разные фильтры ( например, корреляцию), так как риск стратегии увеличивается экспоненциально. Результаты применения коинтеграционного фильтра ведут к большой части дней без сделок, так что нужны большие наборы данных для проверки устойчивости результатов.
Не только институциональные инвесторы имеют проблемы с ликвидностью; частные инвесторы могут столкнуться с другой трудностью - высокими требованиями к ГО при торговле фьючерсами. Позиции по спреду и строго внутридневная система могут помочь уменьшить эти требования.
В конце отметим, что определение коэффициента хэджирования сделано обычным методом наименьших квадратов. Испоьзование обобщенного метода наименьших квадратов (TLS - см. часть1 ) может снизить риски, так как вычисление производится путем решения симметричной задачи оптимизации.
Не является индивидуальной инвестиционной рекомендацией | При копировании ссылка обязательна | Нашли ошибку - выделить и нажать Ctrl+Enter | Жалоба