5 сентября 2016 QuantAlgos
Продолжая мои исследования в области моделирования временных серий, я решил изучить авторегрессивные и условные гетероскедатичные модели. В частности, я взял авторегрессивную модель ARIMA и общую авторегрессивную гетероскедатичную модель GARCH, так как на них часто сылаются в финансовой литературе. Далее следует описание того, что я узнал об этих моделях и основной процесс нахождения их параметров, а также простая торговая стратегия, основанная на предсказаниях полученной модели.
Сначала дадим несколько необходимых определений. Я не хочу воспроизводить всю теорию целиком, ниже дан краткий обзор моделирования временных серий, в частности ARIMA и GARCH моделей:
В первую очередь, вычисление ARIMA и GARCH моделей это способ узнать, при каких прошлых наблюдениях, шуме и дисперсии временной серии возможно предсказать следующее значения этой серии. Такие модели, параметры которых правильно установлены, имеют некоторую предсказательную способность, предполагая, конечно, что эти параметры остаются постоянными на некоторое время для данного процесса.
ARMA модель (пока без "I") - это линейная комбинация авторегрессивной (AR) модели и скользящего среднего (МА). В AR модели предиктором является прошлое значении серии. МА модель структурно схожа с AR моделью, исключая предикторы для шума. Авторегрессивная модель со скользящей средней порядка p,q - ARMA(p,q) - это линейная комбинация упомянутых моделей и определяется как:

ARIMA (p,d,q) модель - это просто ARMA модель, дифференцированная d раз - для получения стационарных серий.
GARCH модель также пытается объяснить гетероскедатичное поведение временной серии ( это характеристика кластерности волатильности) влиянием предыдущих значений серии (описываемых компонентом AR) и белым шумом (описваемым МА компонентом). GARCH модель использует авторегрессивный процесс для дисперсии, то есть использует прошлые значения дисперсии для вычисления будущих значений диспесии этой временной серии.
Далее, в рамках представленного контекста, я найду ARIMA/GARCH модель для EUR/USD пары, и использую ее в качестве основы для торговой стратегии. Параметры модели вычисляются для каждого дня с применением процедуры подгонки, эта модель затем используется для предсказания приращения следующего торгового дня и соответственного вхождения в позицию, которая сохраняется в течение дня. Если предсказание совпадает с предсказанием предыдущего дня, существующая позиция сохраняется.
Скользящее окно логарифма приращений используется для вычисления параметров оптимальной модели ARIMA/GARCH на закрытии каждого торгового дня. Процедура подгонки основана на поиске параметров, которые минимизируют AIC ( информационный критерий Аикаке), но могут быть также применены и другие методы. Например, мы можем выбрать параметры, минимизирующие BIC (байесовский иформационный критерий), который может помочь уменьшить переподгонку в сложных моделях (то есть моделях с большим числом параметров). Такая процедура нахождения параметров была предложена Michael Halls-Moore в посте ARIMA+GARCH trading strategy for the S&P500, и я одолжил у него часть кода.
Я выбрал скользящее окно размером 1000 дней для вычисления модели, но это значение является параметром для оптимизации. Можно взять столько данных, сколько возможно, для скользящего окна, но это может быть не оптимально для установления параметров модели для быстро меняющегося рынка. Я не буду проводить много экспериментов, но было бы интересно иследовать зависимость прибыльности модели от размеров скользящего окна. Далее код на языке R:
Предсказания получаются только для направления: покупаем, когда предсказано положительное приращения и продаем, когда отрицательное. Результат такого подхода в сравнении со стратегией "купил и держи" показано на рисунке в заглавии статьи.
Вы, наверное, заметили, что в процедуре вычисления параметров модели, описанной выше, я запоминал действительные предсказанные значения, так же как и предсказания направления приращения цены. Я хочу исследовать предсказательную способность величины приращения. Точнее, может ли фильтрация сделок, в случаях, когда величина предсказанного приращения ниже определенного порога, улучшить доходность стратегии? Код ниже представляет такой анализ для небольших порогах приращений. Для упрощения, я конвертировал логарифмы приращений в простые приращения, чтобы получить управление знаком предсказания и облегчения применения порога:
И такой результат получился по сравнению с первой стратегией:
Похоже, что рассчитанная нами модель в некоторые дни может описывать лежащий в ее основе процесс лучше, чем в другие. Вероятно, если мы будем отфильтровывать сделки в тех случаях, где наша уверенность в точности модели меньше, то сможем повысить производительность стратегии. Такой подход требует вычисления статистической значимости ежедневного расчета модели, и вход в сделку должен осуществляться после того, как эта значимость превысит определенный порог. Есть несколько путей достижения этой цели. Во-первых, мы можем визуально исследовать коррелограмму остатков модели и вынести суждение о том, насколько хорошо модель соответствует процессу. В идеале, остатки (шум) модели должны быть похожи на белый шум, то есть серийная корреляция должна отсутствовать. Коррелограмма остатков может быть построена в R следующим образом:
Так как визуально эта коррелограмма представляет хорошее соответствие модели процессу, очевидно,что подход, основанный на субъективном суждении, не очень хорош. Лучший способ - проверить модель с помощью стаистики Льюнга-Бокса (Ljung-Box). Статистика Льюнга-Бокса - это проверка гипотезы о том, верно ли утверждение, что автокорреляция остатков вычисленной модели значительно отличается от 0. В этом тесте нулевой гипотезой является предположение, что автокорреляция остатков равна 0, а альтернативой - то, что в процессе имеется серийная корреляция. Отклонение нулевой гипотезы и принятие альтернативы будет значить, что модель не очень хорошо подходит к процессу, так как есть необъясненные структуры в остатках. Статистика Льюнга-Бокса вычисляется в R следующим образом:
В данном случае p-значение говорит о том, что остатки независимы и данная модель имеет хорошее соответствие процессу. Отметим, что статистика Льюнга-Бокса (величина X-squared в вышеприведенном коде) растет сильнее при увеличении автокорреляции остатков. Р-значение - это вероятность получения величины остатка такой же или более статистики при нулевой гипотезе. Таким образом, высокое р-значение является доказательством независимости остатков. Заметьте, что вычисление применяется для всех лагов, начиная с первого, что определено в функции Box.test().
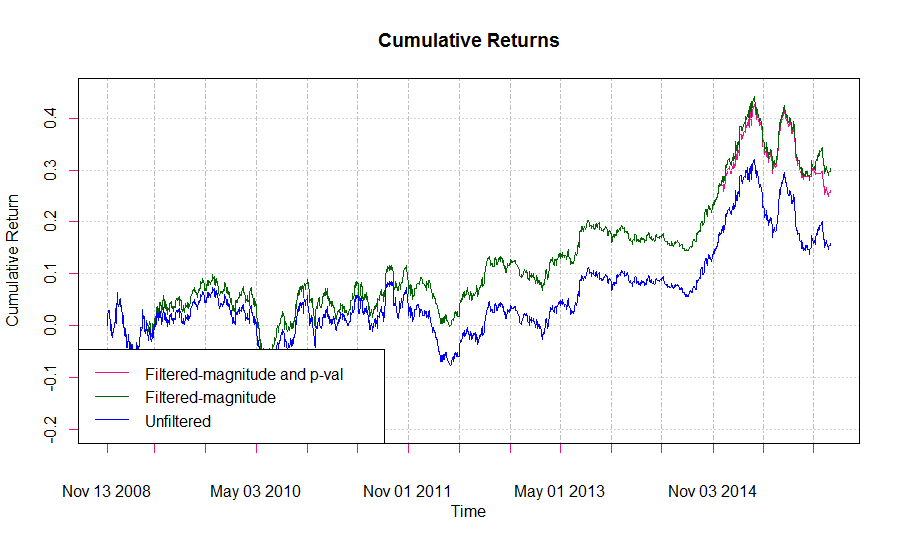
Применяя тест Льюнга-Бокса к модели, пересчитываемой ежедневно, мы получаем очень мало дней, где отвергается нулевая гипотеза о независимости остатков, так что внедрив такой фильтр в нашу стратегию мы получим слабое соответствие модели и вряд ли это улучшит производительность, что и видно на графике в заглавии статьи.
Заключение и направления дальнейших исследований
Производительность стратегии ARMA/GARCH превышает доходность стратегии "купил и держи" на тестируемом периоде пары EUR/USD, хотя и не является слишком впечатляющей. Возможно улучшение доходности стратегии путем фильтрации по таким характеристикам, как величина предсказанного приращения и степень соответствия модели процессу, хотя последнее и не добавило много к конкретному алгоритму. Дополнительным фильтром может служить вычисление 95% доверительного интервала для ежедневного предсказания, и входить в сделку в том случае, если знаки каждого из порогов этого интервала совпадают, хотя это и может значительно уменьшить число сделок.
Есть очень много вариантов модели GARCH, например, экспоненциальная, интегральная, квадратичная, структурная и т.д. Они могут дать лучшее соответствие рассматриваемому процессу, чем простая модель GARCH(1,1), примененная в нашем примере.
Я нахожу очень интересной область исследований, в которой предсказание временной серии осуществляется в результате сложной комбинации различных моделей, например, взятием средней от индивидуального предсказания каждой модели, или поиском консенсуса, или большинством голосов о знаке предсказания. Заимствуя термин из машинного обучения, "ансамбль" моделей может часто генерировать более точное предсказание, чем любая из его составляющих. Возможно полезным подходом будет совмещение предсказаний ARIMA/GARCH модели, представленной здесь, с обученной нейронной сетью или другим обучающимся методом. Мы можем предположить, что ARIMA/GARCH модель объясняет линейные зависимости во временной серии, а нейронная сеть может хорошо поймать зависимости нелинейные.
Сначала дадим несколько необходимых определений. Я не хочу воспроизводить всю теорию целиком, ниже дан краткий обзор моделирования временных серий, в частности ARIMA и GARCH моделей:
В первую очередь, вычисление ARIMA и GARCH моделей это способ узнать, при каких прошлых наблюдениях, шуме и дисперсии временной серии возможно предсказать следующее значения этой серии. Такие модели, параметры которых правильно установлены, имеют некоторую предсказательную способность, предполагая, конечно, что эти параметры остаются постоянными на некоторое время для данного процесса.
ARMA модель (пока без "I") - это линейная комбинация авторегрессивной (AR) модели и скользящего среднего (МА). В AR модели предиктором является прошлое значении серии. МА модель структурно схожа с AR моделью, исключая предикторы для шума. Авторегрессивная модель со скользящей средней порядка p,q - ARMA(p,q) - это линейная комбинация упомянутых моделей и определяется как:

ARIMA (p,d,q) модель - это просто ARMA модель, дифференцированная d раз - для получения стационарных серий.
GARCH модель также пытается объяснить гетероскедатичное поведение временной серии ( это характеристика кластерности волатильности) влиянием предыдущих значений серии (описываемых компонентом AR) и белым шумом (описваемым МА компонентом). GARCH модель использует авторегрессивный процесс для дисперсии, то есть использует прошлые значения дисперсии для вычисления будущих значений диспесии этой временной серии.
Далее, в рамках представленного контекста, я найду ARIMA/GARCH модель для EUR/USD пары, и использую ее в качестве основы для торговой стратегии. Параметры модели вычисляются для каждого дня с применением процедуры подгонки, эта модель затем используется для предсказания приращения следующего торгового дня и соответственного вхождения в позицию, которая сохраняется в течение дня. Если предсказание совпадает с предсказанием предыдущего дня, существующая позиция сохраняется.
Скользящее окно логарифма приращений используется для вычисления параметров оптимальной модели ARIMA/GARCH на закрытии каждого торгового дня. Процедура подгонки основана на поиске параметров, которые минимизируют AIC ( информационный критерий Аикаке), но могут быть также применены и другие методы. Например, мы можем выбрать параметры, минимизирующие BIC (байесовский иформационный критерий), который может помочь уменьшить переподгонку в сложных моделях (то есть моделях с большим числом параметров). Такая процедура нахождения параметров была предложена Michael Halls-Moore в посте ARIMA+GARCH trading strategy for the S&P500, и я одолжил у него часть кода.
Я выбрал скользящее окно размером 1000 дней для вычисления модели, но это значение является параметром для оптимизации. Можно взять столько данных, сколько возможно, для скользящего окна, но это может быть не оптимально для установления параметров модели для быстро меняющегося рынка. Я не буду проводить много экспериментов, но было бы интересно иследовать зависимость прибыльности модели от размеров скользящего окна. Далее код на языке R:
### ARIMA/GARCH trading model
library(quantmod)
library(timeSeries)
library(rugarch)
# get data and initialize objects to hold forecasts
EURUSD <- read.csv('EURUSD.csv', header = T)
EURUSD[, 1] < - as.Date(as.character(EURUSD[, 1]), format="%d/%m/%Y")
returns <- diff(log(EURUSD$C)) ## ttr::ROC can also be used: calculates log returns by default
window.length <- 1000
forecasts.length <- length(returns) - window.length
forecasts <- vector(mode="numeric", length=forecasts.length)
directions <- vector(mode="numeric", length=forecasts.length)
p.val <- vector(mode="numeric", length=forecasts.length)
# loop through every trading day, estimate optimal model parameters from rolling window
# and predict next day's return
for (i in 0:forecasts.length) {
roll.returns <- returns[(1+i):(window.length + i)] # create rolling window
final.aic <- Inf
final.order <- c(0,0,0)
# estimate optimal ARIMA model order
for (p in 0:5) for (q in 0:5) { # limit possible order to p,q <= 5
if (p == 0 && q == 0) next # p and q can't both be zero
arimaFit <- tryCatch( arima(roll.returns, order = c(p,0,q)),
error = function( err ) FALSE,
warning = function( err ) FALSE )
if (!is.logical( arimaFit)) {
current.aic <- AIC(arimaFit)
if (current.aic < final.aic) { # retain order if AIC is reduced
final.aic <- current.aic
final.order <- c(p,0,q)
final.arima <- arima(roll.returns, order = final.order)
}
}
else next
}
# specify and fit the GARCH model
spec = ugarchspec(variance.model <- list(garchOrder=c(1,1)),
mean.model <- list(
armaOrder <- c(final.order[1], final.order[3]), include.mean = T),
distribution.model = "sged")
fit = tryCatch(ugarchfit(spec, roll.returns, solver = 'hybrid'), error = function(e) e, warning = function(w) w)
# calculate next day prediction from fitted mode
# model does not always converge - assign value of 0 to prediction and p.val in this case
if (is(fit, "warning")) {
forecasts[i+1] <- 0
print(0)
p.val[i+1] <- 0
}
else {
next.day.fore = ugarchforecast(fit, n.ahead = 1)
x = [email protected]$seriesFor
directions[i+1] <- ifelse(x[1] > 0, 1, -1) # directional prediction only
forecasts[i+1] <- x[1] # actual value of forecast
print(forecasts[i])
# analysis of residuals
resid <- as.numeric(residuals(fit, standardize = TRUE))
ljung.box <- Box.test(resid, lag = 20, type = "Ljung-Box", fitdf = 0)
p.val[i+1] <- ljung.box$p.value
}
}
dates <- EURUSD[, 1]
forecasts.ts <- xts(forecasts, dates[(window.length):length(returns)])
# create lagged series of forecasts and sign of forecast
ag.forecasts <- Lag(forecasts.ts, 1)
ag.direction <- ifelse(ag.forecasts > 0, 1, ifelse(ag.forecasts < 0, -1, 0))
# Create the ARIMA/GARCH returns for the directional system
ag.direction.returns <- ag.direction * returns[(window.length):length(returns)]
ag.direction.returns[1] <- 0 # remove NA
# Create the backtests for ARIMA/GARCH and Buy & Hold
ag.curve <- log( cumprod( 1 + ag.direction.returns) )
buy.hold.ts <- xts(returns[(window.length):length(returns)], dates[(window.length):length(returns)])
buy.hold.curve <- log(cumprod(1 + buy.hold.ts))
both.curves <- cbind(ag.curve, buy.hold.curve)
names(both.curves) <- c("Strategy returns", "Buy and hold returns")
# plot both curves together
myColors <- c( "darkorange", "blue")
plot(x = both.curves[,"Strategy returns"], xlab = "Time", ylab = "Cumulative Return",
main = "Cumulative Returns", ylim = c(-0.25, 0.4), major.ticks= "quarters",
minor.ticks = FALSE, col = "darkorange")
lines(x = both.curves[,"Buy and hold returns"], col = "blue")
legend(x = 'bottomleft', legend = c("Strategy", "B&H"),
lty = 1, col = myColors)Предсказания получаются только для направления: покупаем, когда предсказано положительное приращения и продаем, когда отрицательное. Результат такого подхода в сравнении со стратегией "купил и держи" показано на рисунке в заглавии статьи.
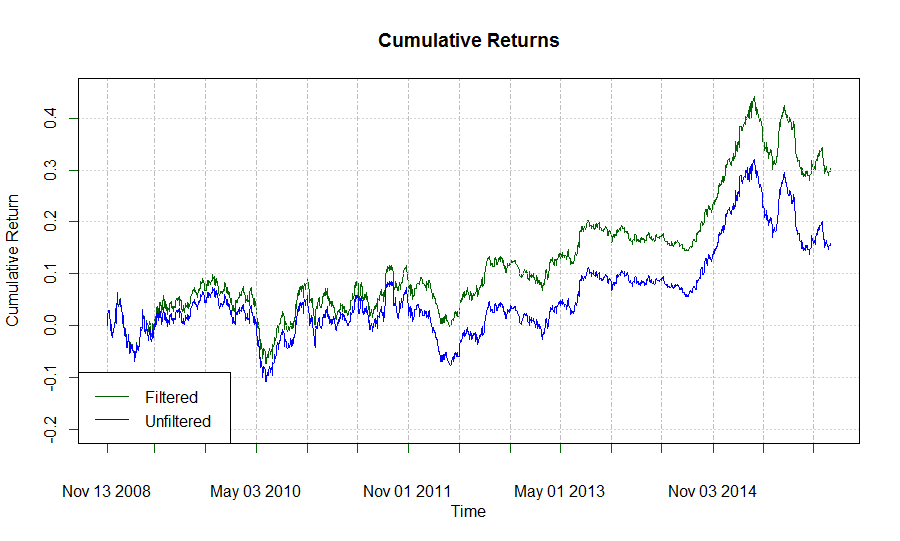
Вы, наверное, заметили, что в процедуре вычисления параметров модели, описанной выше, я запоминал действительные предсказанные значения, так же как и предсказания направления приращения цены. Я хочу исследовать предсказательную способность величины приращения. Точнее, может ли фильтрация сделок, в случаях, когда величина предсказанного приращения ниже определенного порога, улучшить доходность стратегии? Код ниже представляет такой анализ для небольших порогах приращений. Для упрощения, я конвертировал логарифмы приращений в простые приращения, чтобы получить управление знаком предсказания и облегчения применения порога:
# Test entering a trade only when prediction exceeds a threshold magnitude
simp.forecasts <- exp(ag.forecasts) - 1
threshold <- 0.000025
ag.threshold <- ifelse(simp.forecasts > threshold, 1, ifelse(simp.forecasts < -threshold, -1, 0))
ag.threshold.returns <- ag.threshold * returns[(window.length):length(returns)]
ag.threshold.returns[1] <- 0 # remove NA
ag.threshold.curve <- log(cumprod( 1 + ag.threshold.returns))
both.curves <- cbind(ag.threshold.curve, buy.hold.curve)
names(both.curves) <- c("Strategy returns", "Buy and hold returns")
# plot both curves together
plot(x = both.curves[,"Strategy returns"], xlab = "Time", ylab = "Cumulative Return",
main = "Cumulative Returns", major.ticks= "quarters", #
minor.ticks = FALSE, ylim = c(-0.2, 0.45), col = "darkorange")
lines(x = both.curves[,"Buy and hold returns"], col = "blue")
legend(x = 'bottomleft', legend = c("Strategy", "B&H"),
lty = 1, col = myColors)И такой результат получился по сравнению с первой стратегией:
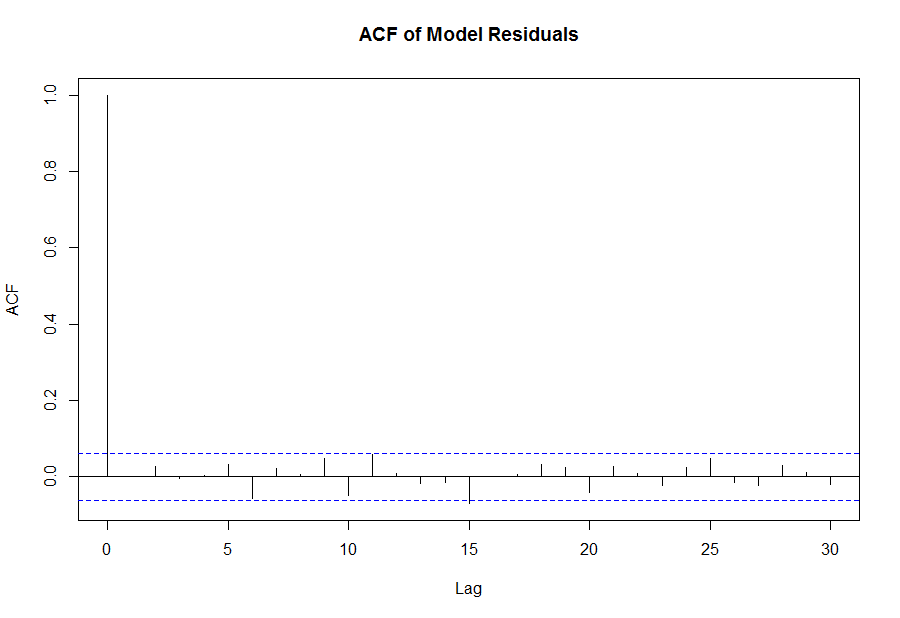
Похоже, что рассчитанная нами модель в некоторые дни может описывать лежащий в ее основе процесс лучше, чем в другие. Вероятно, если мы будем отфильтровывать сделки в тех случаях, где наша уверенность в точности модели меньше, то сможем повысить производительность стратегии. Такой подход требует вычисления статистической значимости ежедневного расчета модели, и вход в сделку должен осуществляться после того, как эта значимость превысит определенный порог. Есть несколько путей достижения этой цели. Во-первых, мы можем визуально исследовать коррелограмму остатков модели и вынести суждение о том, насколько хорошо модель соответствует процессу. В идеале, остатки (шум) модели должны быть похожи на белый шум, то есть серийная корреляция должна отсутствовать. Коррелограмма остатков может быть построена в R следующим образом:
acf([email protected]$residuals, main = 'ACF of Model Residuals')Так как визуально эта коррелограмма представляет хорошее соответствие модели процессу, очевидно,что подход, основанный на субъективном суждении, не очень хорош. Лучший способ - проверить модель с помощью стаистики Льюнга-Бокса (Ljung-Box). Статистика Льюнга-Бокса - это проверка гипотезы о том, верно ли утверждение, что автокорреляция остатков вычисленной модели значительно отличается от 0. В этом тесте нулевой гипотезой является предположение, что автокорреляция остатков равна 0, а альтернативой - то, что в процессе имеется серийная корреляция. Отклонение нулевой гипотезы и принятие альтернативы будет значить, что модель не очень хорошо подходит к процессу, так как есть необъясненные структуры в остатках. Статистика Льюнга-Бокса вычисляется в R следующим образом:
ljung.box <- Box.test(resid, lag = 20, type = "Ljung-Box", fitdf = 0)
ljung.box
Box-Ljung test
data: resid
X-squared = 23.099, df = 20, p-value = 0.284В данном случае p-значение говорит о том, что остатки независимы и данная модель имеет хорошее соответствие процессу. Отметим, что статистика Льюнга-Бокса (величина X-squared в вышеприведенном коде) растет сильнее при увеличении автокорреляции остатков. Р-значение - это вероятность получения величины остатка такой же или более статистики при нулевой гипотезе. Таким образом, высокое р-значение является доказательством независимости остатков. Заметьте, что вычисление применяется для всех лагов, начиная с первого, что определено в функции Box.test().
Применяя тест Льюнга-Бокса к модели, пересчитываемой ежедневно, мы получаем очень мало дней, где отвергается нулевая гипотеза о независимости остатков, так что внедрив такой фильтр в нашу стратегию мы получим слабое соответствие модели и вряд ли это улучшит производительность, что и видно на графике в заглавии статьи.
Заключение и направления дальнейших исследований
Производительность стратегии ARMA/GARCH превышает доходность стратегии "купил и держи" на тестируемом периоде пары EUR/USD, хотя и не является слишком впечатляющей. Возможно улучшение доходности стратегии путем фильтрации по таким характеристикам, как величина предсказанного приращения и степень соответствия модели процессу, хотя последнее и не добавило много к конкретному алгоритму. Дополнительным фильтром может служить вычисление 95% доверительного интервала для ежедневного предсказания, и входить в сделку в том случае, если знаки каждого из порогов этого интервала совпадают, хотя это и может значительно уменьшить число сделок.
Есть очень много вариантов модели GARCH, например, экспоненциальная, интегральная, квадратичная, структурная и т.д. Они могут дать лучшее соответствие рассматриваемому процессу, чем простая модель GARCH(1,1), примененная в нашем примере.
Я нахожу очень интересной область исследований, в которой предсказание временной серии осуществляется в результате сложной комбинации различных моделей, например, взятием средней от индивидуального предсказания каждой модели, или поиском консенсуса, или большинством голосов о знаке предсказания. Заимствуя термин из машинного обучения, "ансамбль" моделей может часто генерировать более точное предсказание, чем любая из его составляющих. Возможно полезным подходом будет совмещение предсказаний ARIMA/GARCH модели, представленной здесь, с обученной нейронной сетью или другим обучающимся методом. Мы можем предположить, что ARIMA/GARCH модель объясняет линейные зависимости во временной серии, а нейронная сеть может хорошо поймать зависимости нелинейные.
Не является индивидуальной инвестиционной рекомендацией | При копировании ссылка обязательна | Нашли ошибку - выделить и нажать Ctrl+Enter | Жалоба