9 мая 2019 smart-lab.ru
В продолжении предыдущей статьи о подбрасывании монетки на языке R, хотелось бы продолжить изучение этого языка и немного углубиться в финансовую математику. Здесь я попробую дать небольшое введение в опционы и их паритет. Не стоит использовать эту статью для изучения опционов, если вы о них не слышали, т.к. могут быть неточности. Надеюсь уважаемые мэтры укажут на них в комментариях.
Зачем нам язык R?
А зачем нам вообще нужен язык R? Строго говоря, он нам не нужен. Но если его освоить, он становится просто еще одним удобным инструментом, как калькулятор или Excel. В прошлой статье были комментарии о том, что лучше использовать C# или Python. Да, я совершенно согласен, именно их и нужно использовать для программирования законченной и оттестированной модели. Но для разработки модели, для экспериментов и для обучения, R подходит как нельзя лучше. Когда строят самолеты, сначала делают деревянный макет, вот для таких макетов и будем использовать R, чтобы убедиться, что взлетит и не тратить силы зря на то, что летать не будет.
Опционы Put и Call, что такое паритет?
Пожалуйста, не читайте это, если вы не знаете, что такое опционы. А если прочтете, не серчайте, если ввёл кого-то в заблуждение.
Сняв с себя ответственность, за неточность дальнейших формулировок, можно теперь сказать, что опцион call — это право покупки актива, по определенной цене. Опцион put — это право продажи актива по определенной цене. Исходя из того, что мы можем покупать и продавать опционы и базовый актив, паритетом опционов называется следующее выражение:
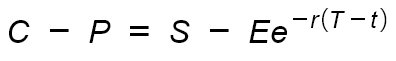
C — опцион Call
P — опцион Put
S — базовый актив
E — страйк, цена исполнения
r — процентная ставка
T, t — время
Другими словами, когда вы покупаете Call и продаете Put на одном страйке, прибыль от роста или падения, будет точно такой же, как если бы вы просто купили базовый актив. Это и есть паритет, т.е. нельзя сделать прибыль из воздуха, всё привязано к цене базового актива.
Но если это выражение не выполняется, возникает возможность арбитража. А арбитраж, как многие наверняка знают, это практически единственный безрисковый способ заработка на рынке.
Моделируем поведение актива
Давайте попробуем смоделировать поведение базового актива. Для этого возьмем формулу, полученную на основе измерения доходности базового актива. Не будем вдаваться в подробности получения этих параметров, это, возможно, станет предметом дальнейшего исследования. На данный момент нам интересно только получить цену каждого очередного шага, что можно сделать по формуле:
μ — drift — дрейф
σ — volatility — волатильность
δt — timestep — временной шаг
Φ — нормально распределенная случайная величина
Это можно записать как (ссылка на код будет в конце статьи):
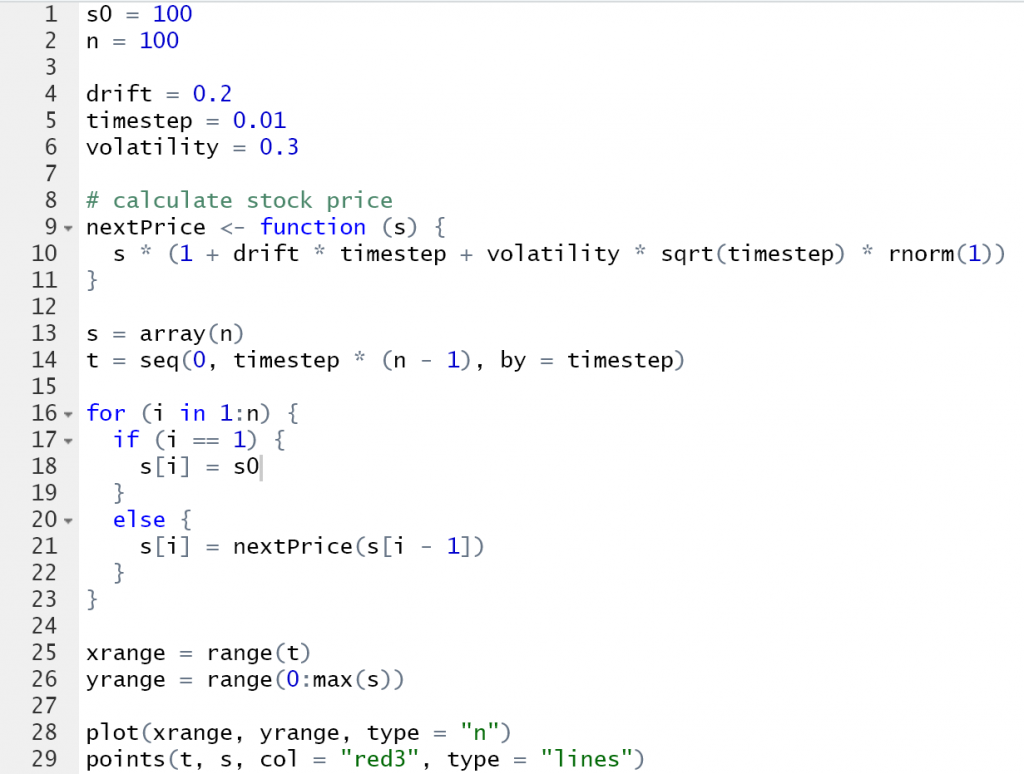
На выходе получаем такой вот график поведения базового актива:
Рассчитываем стоимость опционов
Не будем разжигать споры о применимости формулы Блэка-Шоулза, я знаю, что здесь есть как сторонники, так и противники этой формулы, наша цель просто сделать модель. Для расчета стоимости опционов используем следующие формулы (да, их уже много раз приводили здесь, но я привожу еще раз, для целостности картины):
У нас появились дополнительные параметры, которые нам понадобятся:
N(d) — функция нормального распределения
r — процентная ставка
E — страйк
T — время экспирации
Соединяем всё вместе и строим график
Напишем функции на языке R для этих формул и построим графики.
(часть кода здесь опущена, чтобы не захламлять пост, но его можно посмотреть по ссылке в конце статьи)
Выполним и получим следующий график:
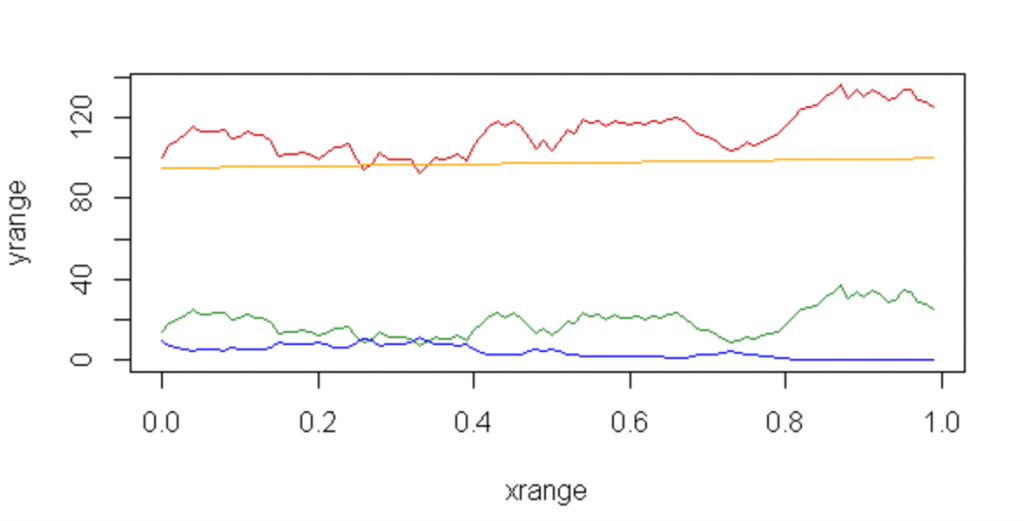
Пояснения к цвету линий:
красная — цена базового актива
зеленая — цена опциона call с экспирацией T
синяя — цена опциона put c экспирацией T
оранжевая — график паритета опционов
Как мы видим на графике, паритет соблюдается независимо от поведения базового актива. И важно заметить, что он сохраняет небольшой рост — это рост благодаря безрисковой процентной ставке, которая обычно равна доходности ОФЗ.
Код можно найти здесь github.com/dmitryy/finance/blob/master/RScripts/put-call-parity.R
/ (C) Источник
Не является индивидуальной инвестиционной рекомендацией
При копировании ссылка обязательна Нашли ошибку: выделить и нажать Ctrl+Enter
Зачем нам язык R?
А зачем нам вообще нужен язык R? Строго говоря, он нам не нужен. Но если его освоить, он становится просто еще одним удобным инструментом, как калькулятор или Excel. В прошлой статье были комментарии о том, что лучше использовать C# или Python. Да, я совершенно согласен, именно их и нужно использовать для программирования законченной и оттестированной модели. Но для разработки модели, для экспериментов и для обучения, R подходит как нельзя лучше. Когда строят самолеты, сначала делают деревянный макет, вот для таких макетов и будем использовать R, чтобы убедиться, что взлетит и не тратить силы зря на то, что летать не будет.
Опционы Put и Call, что такое паритет?
Пожалуйста, не читайте это, если вы не знаете, что такое опционы. А если прочтете, не серчайте, если ввёл кого-то в заблуждение.
Сняв с себя ответственность, за неточность дальнейших формулировок, можно теперь сказать, что опцион call — это право покупки актива, по определенной цене. Опцион put — это право продажи актива по определенной цене. Исходя из того, что мы можем покупать и продавать опционы и базовый актив, паритетом опционов называется следующее выражение:
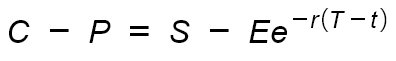
C — опцион Call
P — опцион Put
S — базовый актив
E — страйк, цена исполнения
r — процентная ставка
T, t — время
Другими словами, когда вы покупаете Call и продаете Put на одном страйке, прибыль от роста или падения, будет точно такой же, как если бы вы просто купили базовый актив. Это и есть паритет, т.е. нельзя сделать прибыль из воздуха, всё привязано к цене базового актива.
Но если это выражение не выполняется, возникает возможность арбитража. А арбитраж, как многие наверняка знают, это практически единственный безрисковый способ заработка на рынке.
Моделируем поведение актива
Давайте попробуем смоделировать поведение базового актива. Для этого возьмем формулу, полученную на основе измерения доходности базового актива. Не будем вдаваться в подробности получения этих параметров, это, возможно, станет предметом дальнейшего исследования. На данный момент нам интересно только получить цену каждого очередного шага, что можно сделать по формуле:
μ — drift — дрейф
σ — volatility — волатильность
δt — timestep — временной шаг
Φ — нормально распределенная случайная величина
Это можно записать как (ссылка на код будет в конце статьи):
На выходе получаем такой вот график поведения базового актива:
Рассчитываем стоимость опционов
Не будем разжигать споры о применимости формулы Блэка-Шоулза, я знаю, что здесь есть как сторонники, так и противники этой формулы, наша цель просто сделать модель. Для расчета стоимости опционов используем следующие формулы (да, их уже много раз приводили здесь, но я привожу еще раз, для целостности картины):
У нас появились дополнительные параметры, которые нам понадобятся:
N(d) — функция нормального распределения
r — процентная ставка
E — страйк
T — время экспирации
Соединяем всё вместе и строим график
Напишем функции на языке R для этих формул и построим графики.
(часть кода здесь опущена, чтобы не захламлять пост, но его можно посмотреть по ссылке в конце статьи)
Выполним и получим следующий график:
Пояснения к цвету линий:
красная — цена базового актива
зеленая — цена опциона call с экспирацией T
синяя — цена опциона put c экспирацией T
оранжевая — график паритета опционов
Как мы видим на графике, паритет соблюдается независимо от поведения базового актива. И важно заметить, что он сохраняет небольшой рост — это рост благодаря безрисковой процентной ставке, которая обычно равна доходности ОФЗ.
Код можно найти здесь github.com/dmitryy/finance/blob/master/RScripts/put-call-parity.R
/ (C) Источник
Не является индивидуальной инвестиционной рекомендацией
При копировании ссылка обязательна Нашли ошибку: выделить и нажать Ctrl+Enter