21 августа 2019 smart-lab.ru
Традиционно считается, что задача портфельной оптимизации, или задача Марковица, представляет собой некоторую самостоятельную задачу выбора такого портфеля активов, который обладал бы максимальной доходностью при минимальных рисках.
Прим. В качестве актива могут выступать ценные бумаги (акции), их производные (опционы) или торговые системы.
Решение задачи состоит из двух этапов:
Прогноз доходности и ковариации активов в будущих периодах – то есть построение некоторого набора «слабых» прогностических моделей.
Составление оптимального портфеля в соответствии с некоторой целевой функцией, и ранее полученными оценками. То есть построение такой композиции «слабых» моделей, которая обладала бы наибольшей прогностической силой.
Почему мы используем аналогию портфельной оптимизации с методами машинного обучения — Bag, Boost?! Потому что в действительности (и мы это продемонстрируем) нам абсолютно не важно, насколько хорошо динамику наших временных рядов прогнозируют «слабые» модели – нам важно только то, чтобы ошибки прогнозов наших моделей взаимно компенсировали бы друг друга в некотором интегральном смысле. Иными словами – в случае бустинга – ошибка прогноза линейной композиции была бы минимальной, а в случае портфельной оптимизации – была бы минимальной ошибка прогноза нелинейной композиции (то есть самого портфеля).
Это представление даёт нам право пользоваться сколь угодно неадекватными оценками доходности и риска (ковариации) в решении задач портфельной оптимизации лишь с тем ограничением, что в некоторой композиции они смогут получить максимально адекватный, устойчивый результат.
Прим. Отличие бустинга от бэггинга в том, что бэггинг собирает портфель (Bag) из адекватных, полноценных моделей, каждая из которых самостоятельно описывает действительность, в то время как бустинг, наоборот, пользуется неадекватными моделями, зависимыми друг от друга, самостоятельно действительность не отражающими.
В простой аналогии, если Bagging при решении вопроса проводит демократическую процедуру голосования среди полноценных членов общества, то Boosting, наоборот, идёт за решением вопроса в психиатрическую больницу.
Для решения задачи мы будем использовать MatlabFinancialToolbox, MatlabOptimizationToolbox, методы последовательного линейного и квадратичного программирования, MatlabStatisticsToolbox, MatlabImageProcessingToolboxи др.
Задачу будем решать в самом общем виде (подходящем для оптимизации портфеля любых активов, в т.ч. торговых систем). А именно:
с учётом «без рисковой» ставки (ставки дисконтирования) 2% USD/year,
ограничениями «buy only»,
ограничением кредитного плеча равным 1,
без ограничений оборота (Turnover=1),
без обязательных резервов и ограничений диверсификации (LowerBounds=0),
без учёта стоимости транзакций (Buy/Sell Costs= 0).
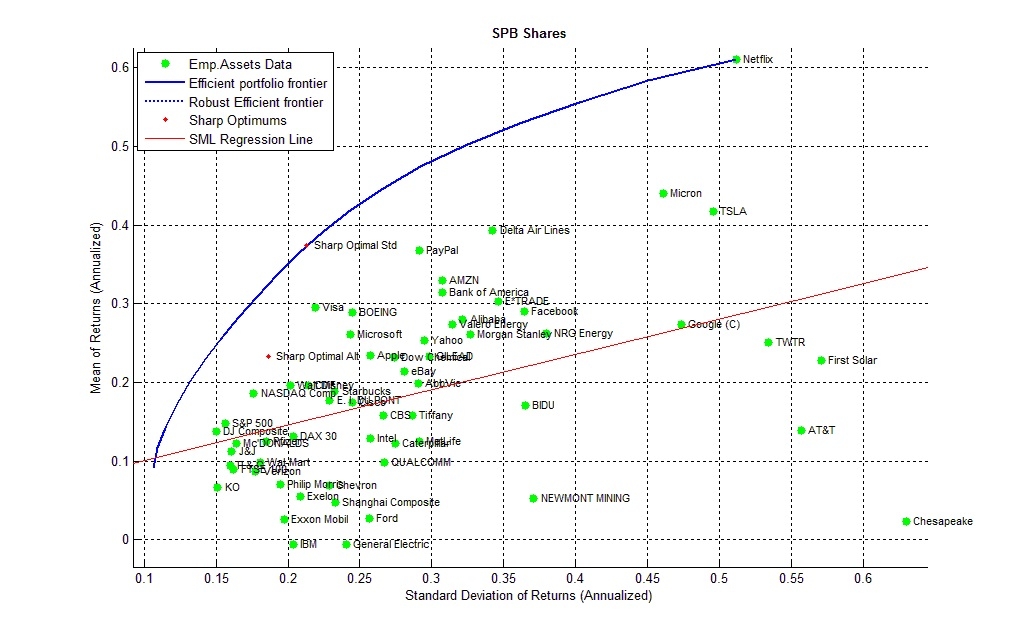
Рис.1. Точечная диаграмма исходных активов в плоскости доход-риск.
Мы имеем исторические котировки акций, торгуемых на Санкт-Петербуржской бирже за последние 6 лет и представленные 64-я основными активами. Эффективная граница Марковица (синяя линия), как ей и полагается, проходит через точку самого высокодоходного актива «Netflix» c уровнем доходности 60% годовых и «риском» 52% годовых и представляет из себя некоторое множество наилучших (с точки зрения доход/«риск») портфелей, которые можно было бы подобрать на исторических данных.
Среди всего множества лучших портфелей нам предстоит выбрать наилучший, в соответствии с критерием показателя Шарпа. То есть такой портфель, который позволял бы получить наибольшую доходность в условиях использования кредитного плеча с соблюдением ограничения по максимальной теоретической просадке. Этот портфель обозначен красной точкой на эффективной границе Марковица и обещает нам доходность 37% годовых, при рисках 22% годовых и показателе Шарпа 1.68 на год.
Тем не менее, валидационный тест (форвард тест) этот стандартный алгоритм выбора оптимального портфеля успешно проваливает, потому что оценки доходности и риска, полученные статистической обработкой данных (Mean-Covariance), даже если они робастные, являются неадекватными – как в узком смысле (то есть не способны прогнозировать поведение активов), так и в широком смысле (то есть на их основании не возможно составить оптимальный портфель).
И в этом нет ничего удивительного – стандартный алгоритм работает только на очень слабо дисперсионных, практически детерминированных данных, для которых стандартные оценки математического ожидания и дисперсии будут адекватными. В случаях же работы со стохастическими случайными величинами, стандартные оценки оказываются очень сильно смещены и, как показывает практика, к стохастическим данным стохастические модели в общем случае оказываются не применимы.
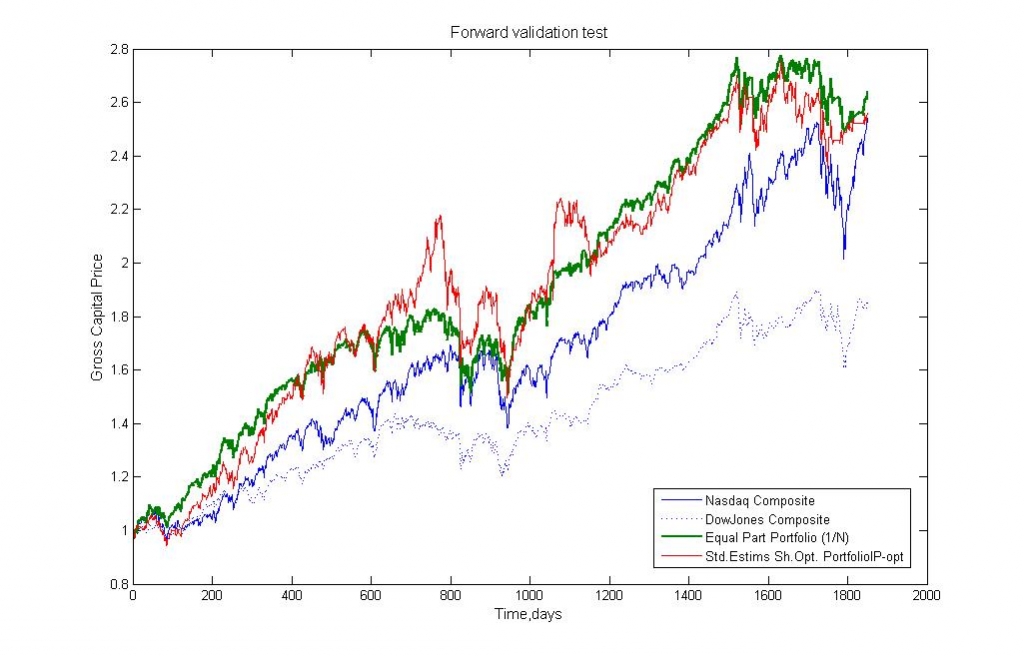
Рис.2. Сравнение динамики стоимости портфелей. Зелёная линия — среднее самих данных, красная линия — оптимизированный по стандартной процедуре (Mean-Variance) портфель.
Как видно из рис.2, даже с регуляризированной ковариационной матрицей (не L2-регуляризация), и робастной оценкой математического ожидания оптимальный портфель по Шарпу (красная кривая) не даёт возможности получить даже средних «по рынку» (зеленая кривая) показателей.
Далее мы будем обозначать этот портфель как «Std. Estims Sh.Opt Portfolio IP-opt», то есть как оптимальный портфель по Шарпу, полученный на стандартной оценке доходностей (среднее прошлых доходностей), с оптимальным инвестиционным периодом (IP-Optimal).
Подбирая другие, более адекватные, оценки будущих доходностей – линейной регрессией (Тrend), скользящей линейной регрессией (MoveTrend), а так же иными моделями, например угловыми оценками, и другими, более устойчивыми оценками ковариации, – можно добиться более приемлемых результатов.
Этим путем нам удалось добиться улучшения показателя Шарпа в 1.26 раза (см. рис.3 и рис.4) по сравнению со средними по данным (средними по «рынку»), получив доходность 34% годовых при максимальной теоретической просадке 21.3%, то есть показателей, очень близких и даже лучших, чем апостериорная оценка параметров оптимального портфеля, построенная на исторически достоверных данных. Таким образом, подобранную композицию моделей оценки мы можем считать абсолютно успешной.

Рис.3. Сравнение динамики стоимости портфелей. Зелёная линия – данные, синяя линия – портфель, подобранный на трендовых оценках доходности, красная линия – портфель, подобранный на стандартных оценках доходности и устойчивых оценках ковариационной матрицы.

Рис.4.
Лучшее решение «Std. Int. Sh.Opt. Portfolio IP-opt» :
В качестве оценки доходности мы берём обычное, не триммированное, смещённое математическое ожидание доходностей за предшествующие 360 календарных дней, в качестве оценки ковариации – некоторую сглаженную (фильтрованную) ковариацию с определённым коэффициентом Калмана (в нашем случае используется не стандартная процедура), лагом кросс ковариации равной нулю и инвестиционным периодом 31 календарный день.
Рис.5 показывает динамику доли актива в портфеле в зависимости от времени, текущему сверху вниз. Если в вертикальном ряду есть отдельные “капли” – значит, актив попадает в портфель нечасто, и долго там не удерживается. Если наблюдаются “струйки” – значит, актив удерживается в портфеле длительный период.
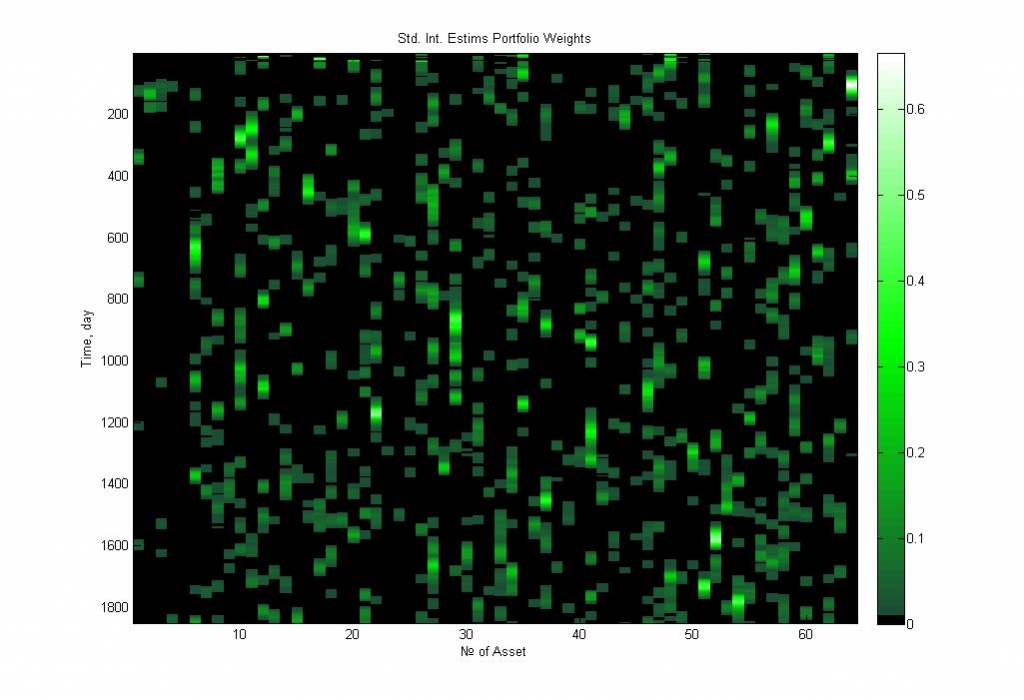
Рис.5. Диаграмма весов активов в лучшем портфеле, демонстрирующая широту диверсификации и частоту перевложений в зависимости от времени (сверху вниз)
Часть 2.
В прошлой части мы подбирали такую комбинацию статистических оценок динамики акций, которая давала нам возможность стабильно выбирать портфель акций лучше среднерыночного, с показателем Шарпа на 26% выше индексного.
Мы также пробовали составлять портфель из портфелей и портфель на основе портфеля оценок, но в силу высокой линейной зависимости оценок и полученных на них портфелей друг от друга Bagging ожидаемо не дал никакого результата.
Тем не менее, этот важный этап подготовительных работ – построение портфеля (или композиции портфелей) на простых, статистических оценках дал нам некоторую отправную точку, относительно которой мы будем рассматривать эффективность всех наших последующих нововведений.
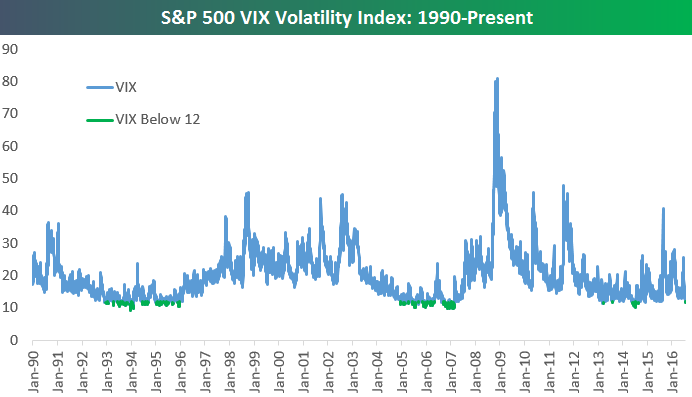
Рис. 6. Иллюстрация динамики волатильности акций США, входящих в состав индекса S&P 500.
Основную проблему стандартных методов мы видим в том, что они разработаны для стационарных стохастических процессов, в то время как любые финансовые (а зачастую природные, биологические и др.), временные ряды имеют нестационарную природу. Так, например, широко известно, что логарифмическое изменение стоимости акций является нестационарным процессом со склонностью к консолидации (кластеризации) волатильности.
В финансовой математике для описания подобного рода явлений широко используются различные авторегрессионные модели – ARCH, GARCH и прочие. Что вполне естественно, так как любая AR модель, например, простая синусоида, будет обладать вышеупомянутым свойством кластеризации.
В этом смысле, вполне естественно, что статистические оценки для подобных нестационарных рядов, полученные средствами, заточенными под ряды стационарные (с постоянной волатильностью), будут сильно искажены, а результаты их применения будут бесполезны. (Простейший портфель показал результаты на валидационном тесте даже хуже среднерыночных)
При этом одних только авторегрессионных моделей волатильности существует порядка сотни, а наряду с ними желаемые распределения с «тяжёлыми хвостами» можно получить с помощью моделей случайной волатильности, например, подбрасывая монетку со случайной ставкой и ещё целого ряда различных методов.
Таким образом, имея такой широкий спектр разнообразных моделей (если они действительно достаточно разнообразны и, соответственно, линейно независимы) мы можем рассчитывать на то, что композиция (Bag/Boost) этих моделей будет обладать намного более высокой обобщающей способностью (прогностической силой), чем каждая из них в отдельности.
Следуя этим рассуждениям, мы подготовили базис из около 50 различных методов оценки риска, доходности и корреляции, учитывающих нестационарность финансовых временных рядов различными способами – от AR-процессов, до оценки рисков по Сортино, – на основе которых впоследствии был построен ряд наиболее устойчивых композиций.
Такой подход позволил нам добиться значительного улучшения показателя Шарпа на рынке NASDAQ по сравнению с портфелем, составленным из простой комбинации простых оценок, но, к сожалению, при линейном переносе полученной композиции на рынок акций ММВБ мы получили далеко не самые лучшие результаты. При этом, новая композиция, заточенная под рынок ММВБ, пересекалась с композицией, заточенной под рынок NASDAQ всего на 30-40%. Что говорит о ещё недостигнутой универсальности методов.
Продемонстрируем полученные результаты на примере 24 голубых фишек, входящих в индекс ММВБ:
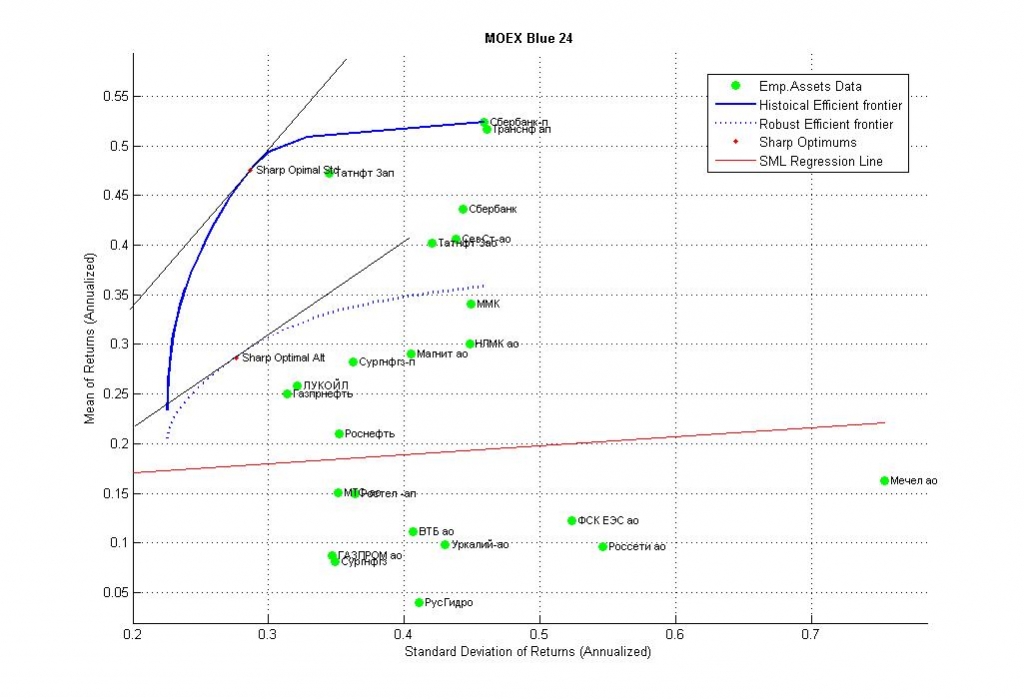
Рис.7. Точечная диаграмма голубых фишек ММВБ в плоскости доход/риск за последние 7 лет (24 фишки).
На графике дополнительно изображена апостериорная эффективная граница портфелей Марковица (синяя кривая), «робастная» апостериорная граница с фильтрацией случайных колебаний доходности (пунктирная) и Security Market Line (красная) в виде линейной регрессии по собственному риску.
На этих данных мы построили ряд портфелей, каждый из которых имеет только три экзогенных переменных (входные параметры) – длинна обучающей выборки, уровень сглаживания (если оно применяется) и оптимальный инвестиционный срок (частота пересмотра портфеля):
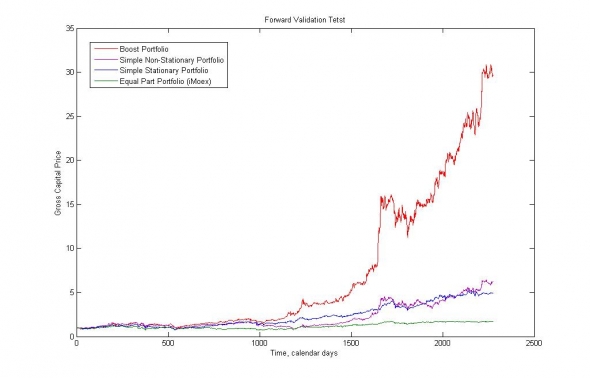
Рис. 8. Демонстрация динамики ликвидационной стоимости портфелей.
Красная – Boost Portfolio – портфель, полученный на сложной композиции нестационарных и стационарных оценок.
Фиолетовая – Simple Non-Stationary Portfolio – портфель, полученный на лучшей комбинации нестационарных оценок, с поправкой на кластеризацию волатильности.
Синяя – Simple Stationary Portfolio – портфель, полученный на лучшей комбинации стандартных оценок.
Зеленая – Equal Part Portfolio – пассивная равновесная стратегия, соответствующая индексу ММВБ (средняя по данным)
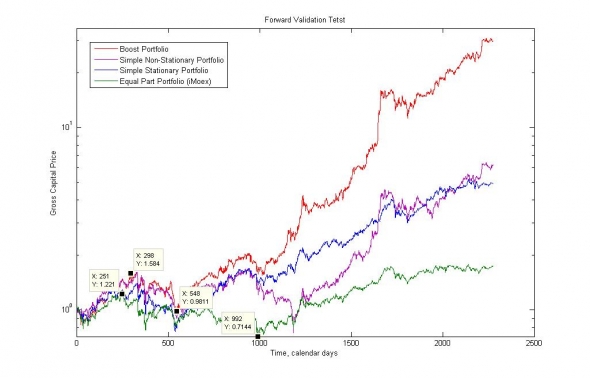
Рис. 9. Демонстрация динамики ликвидационной стоимости портфелей в логарифмическом масштабе. В качестве особых точек выделены точки, соответствующие максимальной просадке индекса и Boost портфеля.

Табл. 2. Статистические характеристики полученных портфелей и предполагаемая максимальная просадка на уровне трёх сигм.
В качестве текущих проблем мы видим:
Низкую универсальность оценочных методик, требующую значительной корректировки при применении к различным рынкам (ММВБ, NASDAQ).
Высокую степень зависимости полученного портфеля от индекса, повторяющую все его убытки.
Отсутствие адекватных методик, не требующих применения подхода Bag/Boost.
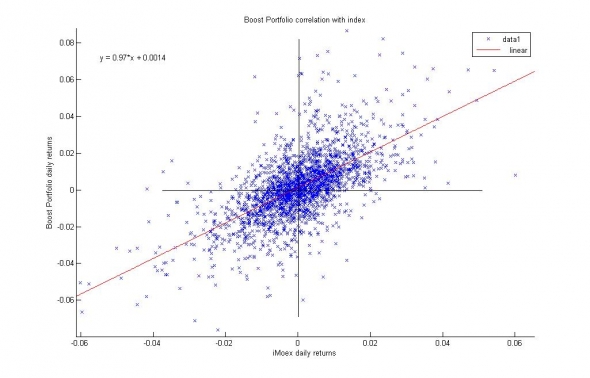
Рис. 10. Корреляция доходности Boost портфеля и индекса iMOEX.
Обычно корреляция снижается путём покупки 20-40% облигаций, но это говорит не о качественном решении задачи управления портфелем ценных бумаг, а об отсутствии такового.
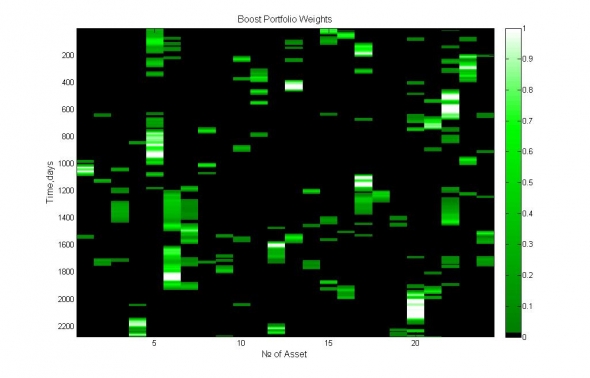
Рис 11. Демонстрация динамики относительных весов активов в Boost портфеле. Время отложено по оси ординат (сверху-вниз), активы – по оси абсцисс.
Видно, что Boost портфель на 80% своего состава преимущественно выбирает две-три, наиболее доходных, некоррелированных акции (из 24), лишь изредка прибегая к концентрированным вложениям в один актив.
Часть 3
Устойчивые долгосрочные модели
В предыдущих частях (часть 1, часть 2) мы рассмотрели построение композитных систем оценок ценных бумаг, построенных при помощи распространённых средств машинного обучения (Bag/Boost методы). Однако, такой подход, несмотря на все свои преимущества (скорость, точность) имеет ряд больших недостатков – отсутствие универсальности моделей в результате проблем «переобучения» (точной настройки на определённые типы рынков и временные интервалы) и сложность интерпретации полученных композиций.
В результате решения этих проблем мы разработали базовую модель на основе наших представлений о стохастических дифференциальных уравнениях с квантовыми скачками, образующих улыбку волатильности. Эта макромодель получила в наших исследованиях наиболее полную микроскопическую интерпретацию.
В то же время Boost часть композиции, состоящая преимущественно из динамических и AR моделей сохранилась в виде надстроечной системы кредитного скоринга, используемой преимущественно в краткосрочных («активных») стратегиях.
Прим. Простейший бинарный кредитный скоринг это: фильтр тренда, фильтр пилы, фильтр плечей и подобные фильтры.
В долгосрочных стратегиях, на рассматриваемых интервалах более полугода и сроках инвестирования более 3-х месяцев (особенно с учётом временного рассеяния сделок), Boost часть полностью теряет свою адекватность. Исключением, разве что, могут оставаться Фурье-фильтры, уберегающие базовую модель от ошибок нахождения трендов внутри бокового движения.
Тем не менее, долгосрочные стратегии, в результате пониженных требований к ликвидности, представляют собой отдельный класс задач, решаемый управляющими крупных взаимных фондов и поэтому заслуживают отдельного рассмотрения.
Для того чтобы оценить применимость модели Марковица в области управления крупным капиталом мы провели серию тестов полученной универсальной событийной модели (без скоринг-фильтров) на российском и американском рынке. Цель – получение дельты к рынку +50% — +100% при улучшении показателя Шарпа.
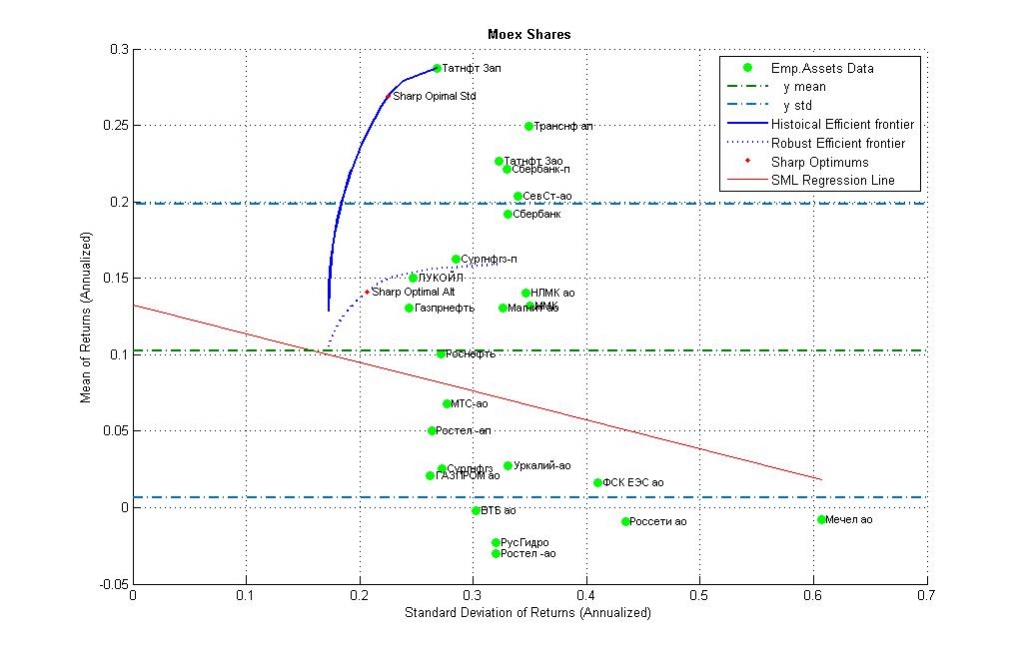
Рис. 13. Изображение распределения активов на российском фондовом рынке внутри исследуемого интервала (In Sample).
В предположении, что мы можем отделить хороший актив, с потенциалом роста, от плохого актива математическое ожидание нашего инвестирования должно составить около:
E[portfolio] = E[market] + 0.8*Std[market] или около 10%+8% = 18% годовых.
(Следствие нормального закона распределения)
Эта же оценка, как ни странно, находится на эффективной робастной границе доходностей, полученной в предположении строгой отраслевой сегментации активов или их иной кластеризации.
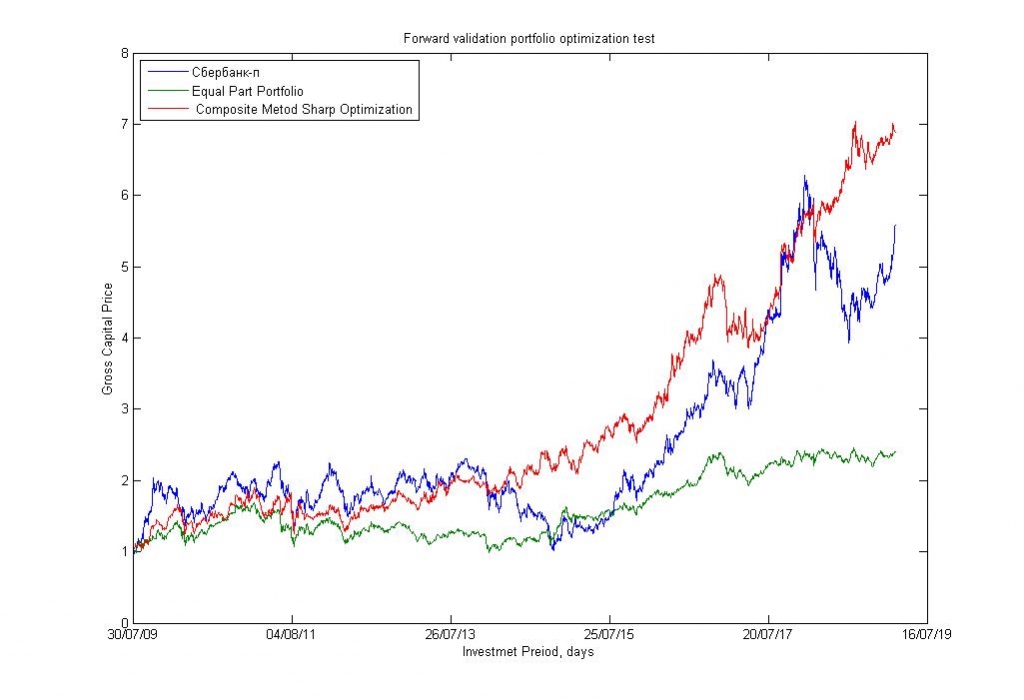
Рис.13. Результаты тестирования стратегии оптимального портфельного инвестирования по Марковицу с ограничением оборота 1.7% на фондовом рынке ММВБ.
Результаты испытаний показывают, что ограничение оборота портфеля ниже 1.5%-2% в день начинают достаточно сильно влиять на результаты стратегии. До этих уровней ограничений, долгосрочные портфели формируются более-менее свободно.
К сожалению, с учётом ликвидности активов не входящих в топ-10 (около 100 млн. руб./день) предел активного управления капиталом наступает уже на уровне около 1.5 млрд. рублей (25 млн. долл. США) – свыше этой суммы уже неминуемо начинается индексное инвестирование, привязанное к ликвидности каждой бумаги.
Прим. В качестве оценки доступной для инвестора ликвидности мы взяли 3% от полной дневной ликвидности ценной бумаги.
В лучшем случае, для активных стратегий с капиталом более 1.5 млрд. рублей, остаётся только активное управление в 10 наиболее ликвидных бумагах, поднимающее оценку предела управляемого капитала до 7-15 млрд. рублей (250 млн. долл. США).
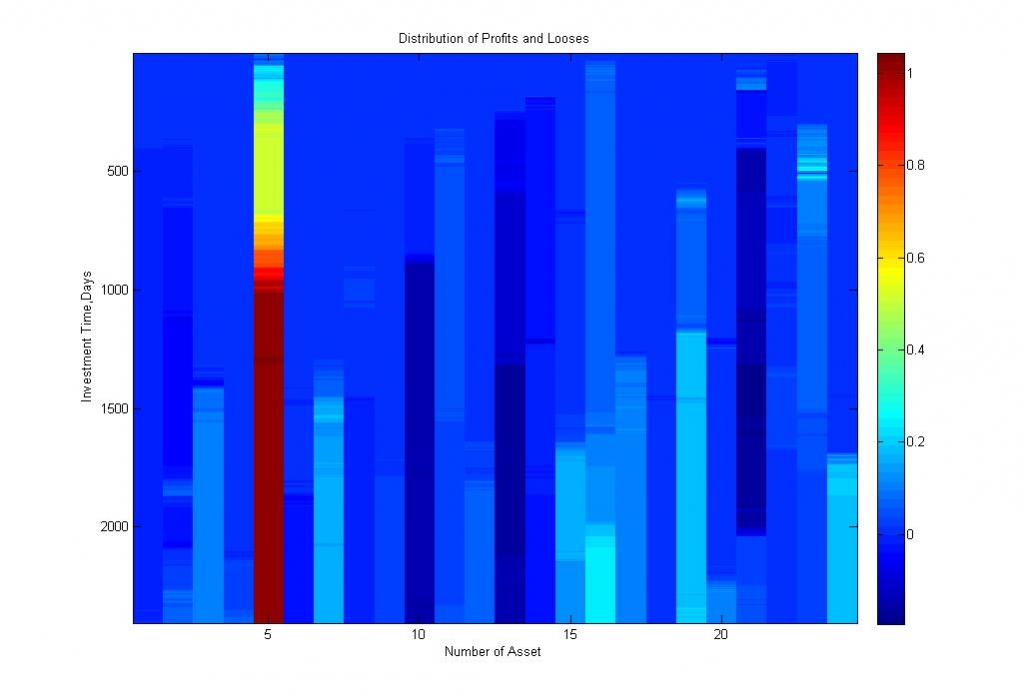
Рис. 14. Тепловая карта финансовых результатов долгосрочного инвестирования в российский рынок ценных бумаг по активам.
Изображение демонстрирует приблизительно 50% использование рынка ценных бумаг долгосрочным портфелем.
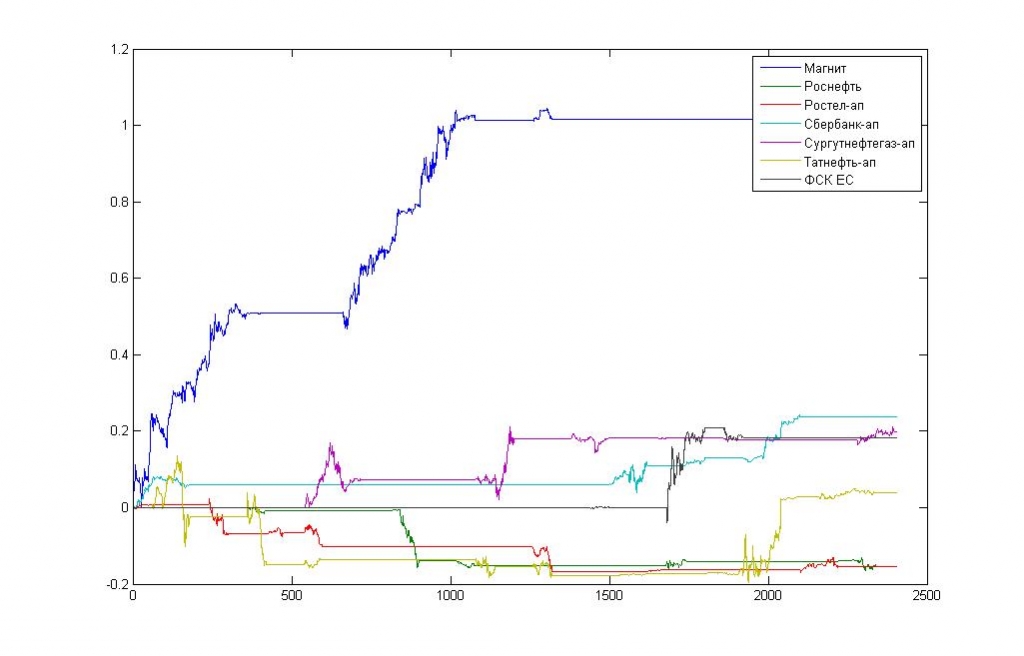
Рис. 15. Основные прибыли и убытки во времени.
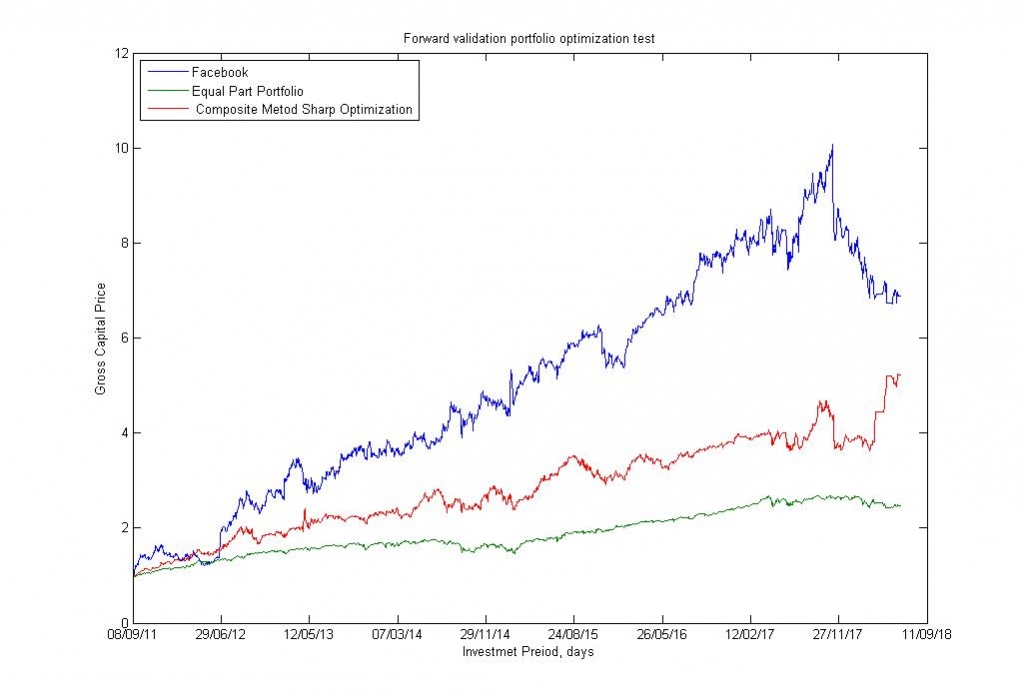
Рис.16. Результаты испытаний полностью идентичной системы на американском фондовом рынке.

Рис.17. Итоговая таблица результатов.
Таким образом, нам удалось достичь требуемой теоретической дельты к рынку (+100%) на долгосрочных системах портфельной оптимизации, не сильно требовательных к ликвидности. К сожалению, предел свободной ликвидности (для торговли без ограничений) на рынках даже для этого типа стратегий начинается очень рано — на уровнях около 1.5 млрд. рублей и 3 млрд. долл. соответственно.
Прим. В качестве актива могут выступать ценные бумаги (акции), их производные (опционы) или торговые системы.
Решение задачи состоит из двух этапов:
Прогноз доходности и ковариации активов в будущих периодах – то есть построение некоторого набора «слабых» прогностических моделей.
Составление оптимального портфеля в соответствии с некоторой целевой функцией, и ранее полученными оценками. То есть построение такой композиции «слабых» моделей, которая обладала бы наибольшей прогностической силой.
Почему мы используем аналогию портфельной оптимизации с методами машинного обучения — Bag, Boost?! Потому что в действительности (и мы это продемонстрируем) нам абсолютно не важно, насколько хорошо динамику наших временных рядов прогнозируют «слабые» модели – нам важно только то, чтобы ошибки прогнозов наших моделей взаимно компенсировали бы друг друга в некотором интегральном смысле. Иными словами – в случае бустинга – ошибка прогноза линейной композиции была бы минимальной, а в случае портфельной оптимизации – была бы минимальной ошибка прогноза нелинейной композиции (то есть самого портфеля).
Это представление даёт нам право пользоваться сколь угодно неадекватными оценками доходности и риска (ковариации) в решении задач портфельной оптимизации лишь с тем ограничением, что в некоторой композиции они смогут получить максимально адекватный, устойчивый результат.
Прим. Отличие бустинга от бэггинга в том, что бэггинг собирает портфель (Bag) из адекватных, полноценных моделей, каждая из которых самостоятельно описывает действительность, в то время как бустинг, наоборот, пользуется неадекватными моделями, зависимыми друг от друга, самостоятельно действительность не отражающими.
В простой аналогии, если Bagging при решении вопроса проводит демократическую процедуру голосования среди полноценных членов общества, то Boosting, наоборот, идёт за решением вопроса в психиатрическую больницу.
Для решения задачи мы будем использовать MatlabFinancialToolbox, MatlabOptimizationToolbox, методы последовательного линейного и квадратичного программирования, MatlabStatisticsToolbox, MatlabImageProcessingToolboxи др.
Задачу будем решать в самом общем виде (подходящем для оптимизации портфеля любых активов, в т.ч. торговых систем). А именно:
с учётом «без рисковой» ставки (ставки дисконтирования) 2% USD/year,
ограничениями «buy only»,
ограничением кредитного плеча равным 1,
без ограничений оборота (Turnover=1),
без обязательных резервов и ограничений диверсификации (LowerBounds=0),
без учёта стоимости транзакций (Buy/Sell Costs= 0).

Рис.1. Точечная диаграмма исходных активов в плоскости доход-риск.
Мы имеем исторические котировки акций, торгуемых на Санкт-Петербуржской бирже за последние 6 лет и представленные 64-я основными активами. Эффективная граница Марковица (синяя линия), как ей и полагается, проходит через точку самого высокодоходного актива «Netflix» c уровнем доходности 60% годовых и «риском» 52% годовых и представляет из себя некоторое множество наилучших (с точки зрения доход/«риск») портфелей, которые можно было бы подобрать на исторических данных.
Среди всего множества лучших портфелей нам предстоит выбрать наилучший, в соответствии с критерием показателя Шарпа. То есть такой портфель, который позволял бы получить наибольшую доходность в условиях использования кредитного плеча с соблюдением ограничения по максимальной теоретической просадке. Этот портфель обозначен красной точкой на эффективной границе Марковица и обещает нам доходность 37% годовых, при рисках 22% годовых и показателе Шарпа 1.68 на год.
Тем не менее, валидационный тест (форвард тест) этот стандартный алгоритм выбора оптимального портфеля успешно проваливает, потому что оценки доходности и риска, полученные статистической обработкой данных (Mean-Covariance), даже если они робастные, являются неадекватными – как в узком смысле (то есть не способны прогнозировать поведение активов), так и в широком смысле (то есть на их основании не возможно составить оптимальный портфель).
И в этом нет ничего удивительного – стандартный алгоритм работает только на очень слабо дисперсионных, практически детерминированных данных, для которых стандартные оценки математического ожидания и дисперсии будут адекватными. В случаях же работы со стохастическими случайными величинами, стандартные оценки оказываются очень сильно смещены и, как показывает практика, к стохастическим данным стохастические модели в общем случае оказываются не применимы.

Рис.2. Сравнение динамики стоимости портфелей. Зелёная линия — среднее самих данных, красная линия — оптимизированный по стандартной процедуре (Mean-Variance) портфель.
Как видно из рис.2, даже с регуляризированной ковариационной матрицей (не L2-регуляризация), и робастной оценкой математического ожидания оптимальный портфель по Шарпу (красная кривая) не даёт возможности получить даже средних «по рынку» (зеленая кривая) показателей.
Далее мы будем обозначать этот портфель как «Std. Estims Sh.Opt Portfolio IP-opt», то есть как оптимальный портфель по Шарпу, полученный на стандартной оценке доходностей (среднее прошлых доходностей), с оптимальным инвестиционным периодом (IP-Optimal).
Подбирая другие, более адекватные, оценки будущих доходностей – линейной регрессией (Тrend), скользящей линейной регрессией (MoveTrend), а так же иными моделями, например угловыми оценками, и другими, более устойчивыми оценками ковариации, – можно добиться более приемлемых результатов.
Этим путем нам удалось добиться улучшения показателя Шарпа в 1.26 раза (см. рис.3 и рис.4) по сравнению со средними по данным (средними по «рынку»), получив доходность 34% годовых при максимальной теоретической просадке 21.3%, то есть показателей, очень близких и даже лучших, чем апостериорная оценка параметров оптимального портфеля, построенная на исторически достоверных данных. Таким образом, подобранную композицию моделей оценки мы можем считать абсолютно успешной.

Рис.3. Сравнение динамики стоимости портфелей. Зелёная линия – данные, синяя линия – портфель, подобранный на трендовых оценках доходности, красная линия – портфель, подобранный на стандартных оценках доходности и устойчивых оценках ковариационной матрицы.

Рис.4.
Лучшее решение «Std. Int. Sh.Opt. Portfolio IP-opt» :
В качестве оценки доходности мы берём обычное, не триммированное, смещённое математическое ожидание доходностей за предшествующие 360 календарных дней, в качестве оценки ковариации – некоторую сглаженную (фильтрованную) ковариацию с определённым коэффициентом Калмана (в нашем случае используется не стандартная процедура), лагом кросс ковариации равной нулю и инвестиционным периодом 31 календарный день.
Рис.5 показывает динамику доли актива в портфеле в зависимости от времени, текущему сверху вниз. Если в вертикальном ряду есть отдельные “капли” – значит, актив попадает в портфель нечасто, и долго там не удерживается. Если наблюдаются “струйки” – значит, актив удерживается в портфеле длительный период.

Рис.5. Диаграмма весов активов в лучшем портфеле, демонстрирующая широту диверсификации и частоту перевложений в зависимости от времени (сверху вниз)
Часть 2.
В прошлой части мы подбирали такую комбинацию статистических оценок динамики акций, которая давала нам возможность стабильно выбирать портфель акций лучше среднерыночного, с показателем Шарпа на 26% выше индексного.
Мы также пробовали составлять портфель из портфелей и портфель на основе портфеля оценок, но в силу высокой линейной зависимости оценок и полученных на них портфелей друг от друга Bagging ожидаемо не дал никакого результата.
Тем не менее, этот важный этап подготовительных работ – построение портфеля (или композиции портфелей) на простых, статистических оценках дал нам некоторую отправную точку, относительно которой мы будем рассматривать эффективность всех наших последующих нововведений.

Рис. 6. Иллюстрация динамики волатильности акций США, входящих в состав индекса S&P 500.
Основную проблему стандартных методов мы видим в том, что они разработаны для стационарных стохастических процессов, в то время как любые финансовые (а зачастую природные, биологические и др.), временные ряды имеют нестационарную природу. Так, например, широко известно, что логарифмическое изменение стоимости акций является нестационарным процессом со склонностью к консолидации (кластеризации) волатильности.
В финансовой математике для описания подобного рода явлений широко используются различные авторегрессионные модели – ARCH, GARCH и прочие. Что вполне естественно, так как любая AR модель, например, простая синусоида, будет обладать вышеупомянутым свойством кластеризации.
В этом смысле, вполне естественно, что статистические оценки для подобных нестационарных рядов, полученные средствами, заточенными под ряды стационарные (с постоянной волатильностью), будут сильно искажены, а результаты их применения будут бесполезны. (Простейший портфель показал результаты на валидационном тесте даже хуже среднерыночных)
При этом одних только авторегрессионных моделей волатильности существует порядка сотни, а наряду с ними желаемые распределения с «тяжёлыми хвостами» можно получить с помощью моделей случайной волатильности, например, подбрасывая монетку со случайной ставкой и ещё целого ряда различных методов.
Таким образом, имея такой широкий спектр разнообразных моделей (если они действительно достаточно разнообразны и, соответственно, линейно независимы) мы можем рассчитывать на то, что композиция (Bag/Boost) этих моделей будет обладать намного более высокой обобщающей способностью (прогностической силой), чем каждая из них в отдельности.
Следуя этим рассуждениям, мы подготовили базис из около 50 различных методов оценки риска, доходности и корреляции, учитывающих нестационарность финансовых временных рядов различными способами – от AR-процессов, до оценки рисков по Сортино, – на основе которых впоследствии был построен ряд наиболее устойчивых композиций.
Такой подход позволил нам добиться значительного улучшения показателя Шарпа на рынке NASDAQ по сравнению с портфелем, составленным из простой комбинации простых оценок, но, к сожалению, при линейном переносе полученной композиции на рынок акций ММВБ мы получили далеко не самые лучшие результаты. При этом, новая композиция, заточенная под рынок ММВБ, пересекалась с композицией, заточенной под рынок NASDAQ всего на 30-40%. Что говорит о ещё недостигнутой универсальности методов.
Продемонстрируем полученные результаты на примере 24 голубых фишек, входящих в индекс ММВБ:

Рис.7. Точечная диаграмма голубых фишек ММВБ в плоскости доход/риск за последние 7 лет (24 фишки).
На графике дополнительно изображена апостериорная эффективная граница портфелей Марковица (синяя кривая), «робастная» апостериорная граница с фильтрацией случайных колебаний доходности (пунктирная) и Security Market Line (красная) в виде линейной регрессии по собственному риску.
На этих данных мы построили ряд портфелей, каждый из которых имеет только три экзогенных переменных (входные параметры) – длинна обучающей выборки, уровень сглаживания (если оно применяется) и оптимальный инвестиционный срок (частота пересмотра портфеля):

Рис. 8. Демонстрация динамики ликвидационной стоимости портфелей.
Красная – Boost Portfolio – портфель, полученный на сложной композиции нестационарных и стационарных оценок.
Фиолетовая – Simple Non-Stationary Portfolio – портфель, полученный на лучшей комбинации нестационарных оценок, с поправкой на кластеризацию волатильности.
Синяя – Simple Stationary Portfolio – портфель, полученный на лучшей комбинации стандартных оценок.
Зеленая – Equal Part Portfolio – пассивная равновесная стратегия, соответствующая индексу ММВБ (средняя по данным)

Рис. 9. Демонстрация динамики ликвидационной стоимости портфелей в логарифмическом масштабе. В качестве особых точек выделены точки, соответствующие максимальной просадке индекса и Boost портфеля.

Табл. 2. Статистические характеристики полученных портфелей и предполагаемая максимальная просадка на уровне трёх сигм.
В качестве текущих проблем мы видим:
Низкую универсальность оценочных методик, требующую значительной корректировки при применении к различным рынкам (ММВБ, NASDAQ).
Высокую степень зависимости полученного портфеля от индекса, повторяющую все его убытки.
Отсутствие адекватных методик, не требующих применения подхода Bag/Boost.

Рис. 10. Корреляция доходности Boost портфеля и индекса iMOEX.
Обычно корреляция снижается путём покупки 20-40% облигаций, но это говорит не о качественном решении задачи управления портфелем ценных бумаг, а об отсутствии такового.

Рис 11. Демонстрация динамики относительных весов активов в Boost портфеле. Время отложено по оси ординат (сверху-вниз), активы – по оси абсцисс.
Видно, что Boost портфель на 80% своего состава преимущественно выбирает две-три, наиболее доходных, некоррелированных акции (из 24), лишь изредка прибегая к концентрированным вложениям в один актив.
Часть 3
Устойчивые долгосрочные модели
В предыдущих частях (часть 1, часть 2) мы рассмотрели построение композитных систем оценок ценных бумаг, построенных при помощи распространённых средств машинного обучения (Bag/Boost методы). Однако, такой подход, несмотря на все свои преимущества (скорость, точность) имеет ряд больших недостатков – отсутствие универсальности моделей в результате проблем «переобучения» (точной настройки на определённые типы рынков и временные интервалы) и сложность интерпретации полученных композиций.
В результате решения этих проблем мы разработали базовую модель на основе наших представлений о стохастических дифференциальных уравнениях с квантовыми скачками, образующих улыбку волатильности. Эта макромодель получила в наших исследованиях наиболее полную микроскопическую интерпретацию.
В то же время Boost часть композиции, состоящая преимущественно из динамических и AR моделей сохранилась в виде надстроечной системы кредитного скоринга, используемой преимущественно в краткосрочных («активных») стратегиях.
Прим. Простейший бинарный кредитный скоринг это: фильтр тренда, фильтр пилы, фильтр плечей и подобные фильтры.
В долгосрочных стратегиях, на рассматриваемых интервалах более полугода и сроках инвестирования более 3-х месяцев (особенно с учётом временного рассеяния сделок), Boost часть полностью теряет свою адекватность. Исключением, разве что, могут оставаться Фурье-фильтры, уберегающие базовую модель от ошибок нахождения трендов внутри бокового движения.
Тем не менее, долгосрочные стратегии, в результате пониженных требований к ликвидности, представляют собой отдельный класс задач, решаемый управляющими крупных взаимных фондов и поэтому заслуживают отдельного рассмотрения.
Для того чтобы оценить применимость модели Марковица в области управления крупным капиталом мы провели серию тестов полученной универсальной событийной модели (без скоринг-фильтров) на российском и американском рынке. Цель – получение дельты к рынку +50% — +100% при улучшении показателя Шарпа.

Рис. 13. Изображение распределения активов на российском фондовом рынке внутри исследуемого интервала (In Sample).
В предположении, что мы можем отделить хороший актив, с потенциалом роста, от плохого актива математическое ожидание нашего инвестирования должно составить около:
E[portfolio] = E[market] + 0.8*Std[market] или около 10%+8% = 18% годовых.
(Следствие нормального закона распределения)
Эта же оценка, как ни странно, находится на эффективной робастной границе доходностей, полученной в предположении строгой отраслевой сегментации активов или их иной кластеризации.

Рис.13. Результаты тестирования стратегии оптимального портфельного инвестирования по Марковицу с ограничением оборота 1.7% на фондовом рынке ММВБ.
Результаты испытаний показывают, что ограничение оборота портфеля ниже 1.5%-2% в день начинают достаточно сильно влиять на результаты стратегии. До этих уровней ограничений, долгосрочные портфели формируются более-менее свободно.
К сожалению, с учётом ликвидности активов не входящих в топ-10 (около 100 млн. руб./день) предел активного управления капиталом наступает уже на уровне около 1.5 млрд. рублей (25 млн. долл. США) – свыше этой суммы уже неминуемо начинается индексное инвестирование, привязанное к ликвидности каждой бумаги.
Прим. В качестве оценки доступной для инвестора ликвидности мы взяли 3% от полной дневной ликвидности ценной бумаги.
В лучшем случае, для активных стратегий с капиталом более 1.5 млрд. рублей, остаётся только активное управление в 10 наиболее ликвидных бумагах, поднимающее оценку предела управляемого капитала до 7-15 млрд. рублей (250 млн. долл. США).

Рис. 14. Тепловая карта финансовых результатов долгосрочного инвестирования в российский рынок ценных бумаг по активам.
Изображение демонстрирует приблизительно 50% использование рынка ценных бумаг долгосрочным портфелем.

Рис. 15. Основные прибыли и убытки во времени.

Рис.16. Результаты испытаний полностью идентичной системы на американском фондовом рынке.

Рис.17. Итоговая таблица результатов.
Таким образом, нам удалось достичь требуемой теоретической дельты к рынку (+100%) на долгосрочных системах портфельной оптимизации, не сильно требовательных к ликвидности. К сожалению, предел свободной ликвидности (для торговли без ограничений) на рынках даже для этого типа стратегий начинается очень рано — на уровнях около 1.5 млрд. рублей и 3 млрд. долл. соответственно.
Не является индивидуальной инвестиционной рекомендацией | При копировании ссылка обязательна | Нашли ошибку - выделить и нажать Ctrl+Enter | Жалоба

