Продолжаем цикл статей, посвящённых решению экономических задач ЕГЭ по математике профильного уровня. Задачи для разбора взяты из реальных вариантов ЕГЭ прошлых лет, которые размещены на популярном среди школьников и учителей сайте РЕШУ ЕГЭ.
Приведённые в данной статье задачи в очередной раз показывают, что задания № 15 (2022–2023 гг.) могут быть разными по содержанию.
Задача 1. Рассчитать наибольший общий объём выходящей информации, если известен общий объём входящей информации.
Решение
Пусть на сервере № 1 обрабатывается x2 Гбайт, на сервере № 2 — y2 Гбайт информации, а S Гбайт — это общий объём выходящей информации.
Имеем систему уравнений:
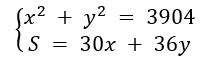
Из первого уравнения системы выразим y и подставим его во второе уравнение.
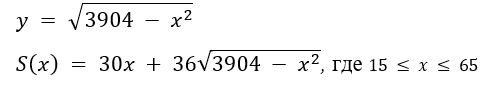
Исследуем функцию S(x) на экстремум.
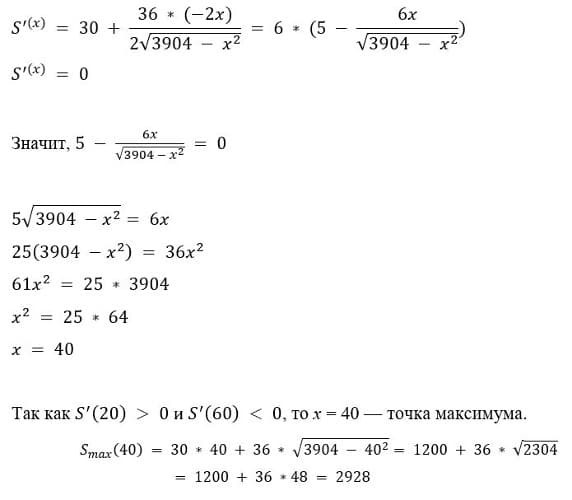
Ответ: 2928 Гбайт.
Следующую задачу решим без использования производной, учитывая тот факт, что объём выходящей (обработанной) информации является квадратом натурального числа.
Задача 2. Рассчитать наибольший общий объём выходящей информации, если известен общий объём входящей информации.
Первичная информация разделяется по серверам № 1 и № 2 и обрабатывается на них. С сервера № 1 при объёме t2 Гбайт входящей в него информации выходит 20t Гбайт, а с сервера № 2 при объёме t2 Гбайт входящей в него информации выходит 21t Гбайт обработанной информации, 25 < t < 55. Каков наибольший общий объём выходящей информации при общем объёме входящей информации в 3364 Гбайт?
Решение
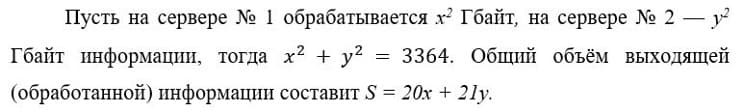
Учитывая, что 3364 = 582, имеем уравнение окружности с центром в начале координат, радиус которой равен 58.
Уравнение S = 20x + 21y представляет собой уравнение не одной прямой, а с семейством параллельных прямых.
Следует найти наибольшее значение S, при котором прямая имеет общие точки с окружностью. Из всех прямых семейства, пересекающих окружность, наибольшее значение S будет достигаться при касании прямой к окружности.
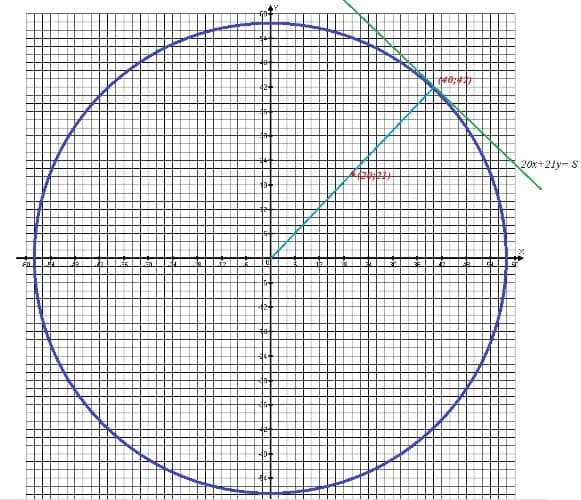
Данная точка — точка касания, в которой достигается наибольшее значение S. При этом условия 25 < 40 < 55 и 25 < 42 < 55 выполняются.
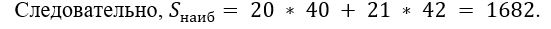
Ответ: 1682 Гбайт.
Классическим способом решения задач на оптимизацию является исследование целевой функции при помощи производной. Однако, как видно из решения задачи № 2, при определённых условиях возможно обращение к более рациональному методу.
https://journal.open-broker.ru/ (C)
Не является индивидуальной инвестиционной рекомендацией
При копировании ссылка обязательна Нашли ошибку: выделить и нажать Ctrl+Enter
Приведённые в данной статье задачи в очередной раз показывают, что задания № 15 (2022–2023 гг.) могут быть разными по содержанию.
Задача 1. Рассчитать наибольший общий объём выходящей информации, если известен общий объём входящей информации.
Решение
Пусть на сервере № 1 обрабатывается x2 Гбайт, на сервере № 2 — y2 Гбайт информации, а S Гбайт — это общий объём выходящей информации.
Имеем систему уравнений:
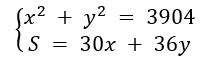
Из первого уравнения системы выразим y и подставим его во второе уравнение.
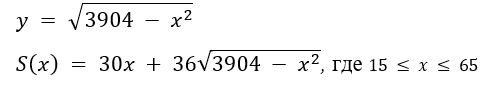
Исследуем функцию S(x) на экстремум.
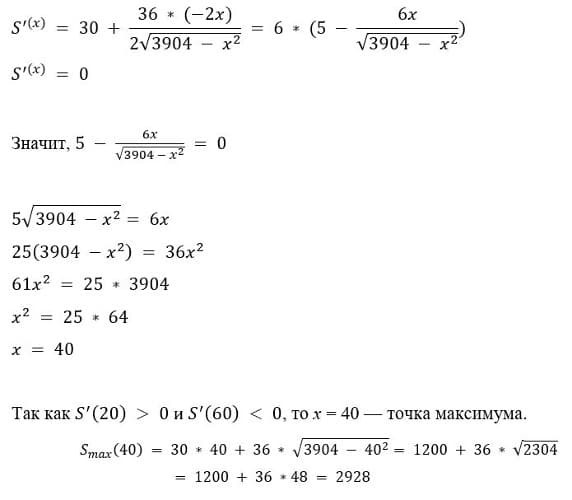
Ответ: 2928 Гбайт.
Следующую задачу решим без использования производной, учитывая тот факт, что объём выходящей (обработанной) информации является квадратом натурального числа.
Задача 2. Рассчитать наибольший общий объём выходящей информации, если известен общий объём входящей информации.
Первичная информация разделяется по серверам № 1 и № 2 и обрабатывается на них. С сервера № 1 при объёме t2 Гбайт входящей в него информации выходит 20t Гбайт, а с сервера № 2 при объёме t2 Гбайт входящей в него информации выходит 21t Гбайт обработанной информации, 25 < t < 55. Каков наибольший общий объём выходящей информации при общем объёме входящей информации в 3364 Гбайт?
Решение
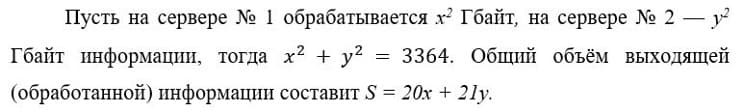
Учитывая, что 3364 = 582, имеем уравнение окружности с центром в начале координат, радиус которой равен 58.
Уравнение S = 20x + 21y представляет собой уравнение не одной прямой, а с семейством параллельных прямых.
Следует найти наибольшее значение S, при котором прямая имеет общие точки с окружностью. Из всех прямых семейства, пересекающих окружность, наибольшее значение S будет достигаться при касании прямой к окружности.
Данная точка — точка касания, в которой достигается наибольшее значение S. При этом условия 25 < 40 < 55 и 25 < 42 < 55 выполняются.
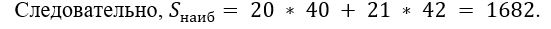
Ответ: 1682 Гбайт.
Классическим способом решения задач на оптимизацию является исследование целевой функции при помощи производной. Однако, как видно из решения задачи № 2, при определённых условиях возможно обращение к более рациональному методу.
https://journal.open-broker.ru/ (C)
Не является индивидуальной инвестиционной рекомендацией
При копировании ссылка обязательна Нашли ошибку: выделить и нажать Ctrl+Enter