1. Как известно, все счастливые годы счастливы одинаково, а каждый интересный – интересен по-своему. Из интересных 90-х первый запомнился «внезапной остановкой» советской власти, включавшей в себя 1/6 суши (плюс, как тогда шутили, 5/6 чуши), второй – «освобожденными» ценами на потребтовары, в итоге гордо выпрямившимися аж в 26.5 раз (по официальным данным), а третий – пальбой из пушек в центре Москвы, каковую местные старожилы (годящиеся, как известно, лишь на то, чтобы чего-нибудь «не припомнить», примерно как неведомые «эксперты» - утверждать) не припоминали тут, если не со времен набегов Девлет-гирея и разбойника Кудеяра, то, по крайней мере, с осени 1917 года.
Тем не менее, куда как более любопытен для экономистов и околоэкономических математиков тишайший 1994-ый, ставший «годом финансовых пирамид», 20-летию которых давайте и посвятим эту запись.
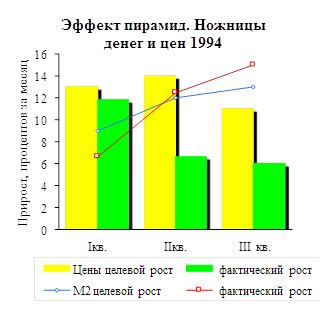
Макроэкономическое значение пирамид, основной размах которых пришелся на весну-лето-начало осени того года, иногда недооценивается. Между тем внезапно выросшая склонность граждан к сбережению неожиданно возымела мощное дезинфляционное действие (см. график). Его правительство поспешило выдать, а комментаторы принять, за первые успехи стабилизационной, или, как тогда выражались, «умеренно-жесткой» финансовой политики. Поворот к такой политике стал возможен в октябре предыдущего года - после разгона Верховного Совета, в целях поддержки отечественных сельхоз- и прочих товаропроизводителей и отечественных же бедняков, распихивавшего деньги налево и направо.
Но до настоящей стабилизации было еще далеко. Она случилась лишь в результате «антикризисного бездействия» правительства Примакова-Маслюкова, не сделавшего в силу своей старческой прокрастинации абсолютно ничего, в т.ч. так и не озаботившегося регулярно проводившейся до этого индексацией доходов населения. И это был ключ к успеху. К концу их пребывания у кормила средние по стране зарплаты и пенсии обесценились до вполне коммунистических 51 и 17 долл. в мес. соотв., и инфляция стала быстро снижаться сама собой, правда – вместе с продолжительностью среднероссийской жизни.
Поздней же осенью 1994, лишившись возможности утекать в пирамиды, деньги хлынули сначала на валютный рынок, устроивши там «черный вторник» (11 октября доллар вздорожал за день на 39%, а к курсу начала года - более чем втрое), а затем – и на потребительский. Инфляция в последнем квартале 1994 взлетела до невиданных уже целый год 16% в месяц (=500% год.). До народного восстания обманутых клиентов пирамид, как 2 года спустя в братской (некогда) Албании, распространившегося затем на Косово и Метохию, и завершившегося печально известными натовскими бомбежками весной 1999, дело у нас, правда, не дошло. Но козлы отпущения за такую «стабилизацию» в министерстве финансов и в ЦБ были найдены, и (времена теперь гуманные, так что, к счастью, оба эти весьма достойных человека до сих здравствуют) с позором изгнаны.
2. Подчеркнем разницу упомянутых в заголовке терминов, поскольку в популярных статьях эти понятия иногда фигурируют как синонимы. Термин «пузырь» прилагается к движению цен, основанных (исключительно) на ожиданиях. Он – вопреки, может быть, распространенному мнению - не требует для своего подержания и «надувания» притока денег (инвестиций), а представляет собой исключительно психологический феномен, чаще всего сопровождающие появление неких (финансовых) изобретений, инноваций, таких, как интернет-компании в конце 90-х или bitcoin’ы в наши дни. Выражение «хлынувшие/напечатанные (ФРС) деньги надули пузырь» - абсурдно, и по его употреблению вы всегда можете легко узнать, является ли произноситель сего экономистом, затратившим некоторые усилия на свое обучение, или всего лишь выдает себя за такового.
Для фиксации цены в пузыре может и не требоваться особо объемных покупок и продаж, а в принципе может быть и вообще достаточно одной публичной сделки держателя такого актива с самим собой (т.е. без участия движения денег вообще). Рост оцениваемого богатства в пузыре основан исключительно на субъективных ожиданиях, и нет ничего и никого, кто бы этот рост обещал. Никаких физических, или, точнее – математических пределов росту пузыря нет – только мало изученные законы психологии стада.
Обычно «пузырь» предполагает неограниченность срока жизни соответствующего актива и возможность его накопления (конечно, в некоем математическом смысле, поскольку ничего вечного в этом мире не бывает, и все что имело начало, будет иметь и конец). Поэтому пузыри не могут надуваться в ценах товаров, уничтожаемых в процессе использования, таких как нефть (и, соответственно, в производных инструментах от этих цен). Разве что очень коротко живущие, сопровождаемые накоплением физических запасов, которые в случае нефти не так удобно хранить, как в случае золота. Примерно то же можно сказать про финансовые инструменты с ограниченным сроком жизни (облигации, CDS), где, тем не менее, можно наблюдать сходные с пузырями движения цен, основанные на вероятностях ожиданий.
Однако тут есть один нюанс – в ценах нефти, золота или жилья присутствует рентная компонента, отражающая ограниченность оставшихся запасов, или земельных участков под застройку в историческом центре Москвы. В итоге цена, скажем, нефти не имеет почти никакого отношения к стоимости ее добычи, а стоимость квартиры где-нибудь рядом с ХХС – к стоимости строительства. Эту рентную компоненту спотовый рынок (т.е. кривая баланса спроса предложения) не умеет вычислять, по крайне мере – краткосрочно. Повышенная волатильность таких цен также может приниматься за пузыри. И в общем-то нет статистических тестов, которые позволяли бы надежно отличить пузырь от других гипотез, объясняющих повышенную волатильность цен (несмотря на обширную литературу по этому пункту).
Существуют ли вообще «пузыри»? В давнем уже интервью Джин Фама, который, пожалуй, мог бы считаться авторитетом в этом вопросе, заметил, что он не знает, что такое пузыри, поскольку они не существуют как предсказуемые (или по крайней мере – идентифицируемые во время своего существования) явления. В общем ситуация с пузырями напоминает ситуацию с жопой – слово есть, и даже математические модели для описания – тоже есть, а самого феномена, пожалуй, что и нет.
3. Термин «финансовая пирамида» описывает инвестиционный фонд, обещающий своим участникам больше, чем может выплатить, и платящий за счет притока новых вкладов. Фактические активы фонда расходятся с «обещанными», т.е. той суммой, которую, как думают вкладчики, им принадлежит. Ясно, что под это определение подпадает и любой банк, обязательства которого превышают активы (т.е. с отрицательным капиталом), как, например, аннулированный недавно по признакам «пирамидальности» Мастер-Банк. Ключевыми характеристиками при математическом описании развития пирамиды как раз являются скорость притока и оттока депозитов, которые не существенны для развития пузыря, а также «обещанная» доходность вкладов – в отличие от пузыря, где никто никаких обещаний не дает и по итогам действа никого не судят.
Говоря о кочующих из статьи в статью примерах пузырей, можно, помимо наиболее известного пузыря с 6-тсячелетней историей – золота, сослаться на «тюльпанную лихорадку» (график справа), пузырь компании Южных морей, созданной для свопирования (обмена на акции компании) облигаций госдолга Англии, знаменитый тем, что в нем прогрел сам Ньютон, и многие другие. К слову сказать, любой госдолг обычно выстроен как пирамида, хотя и не является пузырем. Правда, у государства есть гораздо больше средств избежать явного дефолта, чем у частного фонда – оно может (хотя и далеко не всегда) перейти к бюджету с первичным профицитом, направляемым на сокращение долга, либо воспользоваться инфляционным налогом, прибегнув к эмиссии. Во всяком случае в модель пирамиды, которую рассмотрим ниже, госдолг не ложится.
[img]http://bcs-express.ru/image.ashx?id=10995[/img]
Пузырем, который следует отнести скорее к пирамидам, была возникшая парой лет раньше во Франции Миссисипская компания, изобретённая небезызвестным Джоном Ло, сделавшего ее акции активом учрежденного им же местного ЦБ (тоже частного), выпускавшего обеспеченные ими деньги. Он, помимо прочего, отметился и в истории экономической мысли, как человек, выдвинувший теорию монетарного стимулирования производства и замену золотых денег кредитными (став основоположником т.н. бумажноденежного меркантилизма), опередив свое время лет эдак на 200 с гаком.
Вроде бы, еще до того, как удариться в бега, он приглашался Петром на должность Минфина России, но, кажется, никаких документальных подтверждений эта байка не имеет. Крах этой пирамиды наложил свой отпечаток на всю историю Франции и менталитет французов – Луи 15-й на дух не принимал каких-либо денег, кроме металлических, в итоге страна погрузилась в дефляцию и депрессию, кончившиеся революцией. В конце 30-х уже 20-го века страны «золотого блока» с Францией во главе снова дольше других находились в дефляции, в итоге войну 1939 страна встретила с экономикой, находившейся в весьма депрессивном состоянии, и всем было, как говорится, «немного не до того». Ну и, наконец, Жак Рюэфф, наиболее видный французский экономист и советник Де Голля (еврей, разумеется - как и почти все остальные участники сложной эпопеи изобретения современных международных денег), еще в 1960-х мечтал о с возрождении давно уже мёртвого золотого стандарта образца до 1914, и надоумил своего шефа обменять долларовую ликвидность на золото. В сентябре 1963 года де Голль приказал Банку Франции требовать от американцев, чтобы 80% процентов дефицита платежного баланса США в отношении Франции покрывались золотом. Ну и т.п.
Говоря о пирамидах, нельзя не упомянуть о Карле Понци, который, собственно и дал свое имя подобным схемам. Строго говоря, схема финансовой пирамиды несколько отлична от схемы Понци – она предполагает, что участник получает доход от привлечения последующих участников, по такой схеме работала популярная у нас 90-х торговля «Гербалайфом» (на сегодня пирамидальность не доказана в суде). Но у нас термин «пирамида» закрепился именно за схемами Понци (где один организатор взаимодействует со всеми участниками, а не выстраивает иерархию), так что не будем плодить дополнительных сущностей без особой надобности. Тем более, что наши «понцестроители» не уступали в изобретательности заокеанским, и уж в этом деле Россия вполне может считаться родиной слонов. На «процессе Рыкова» репортером подрабатывал сам А.П.Чехов.
Ну и довольно свежий пирамидальный скандал с фондом основателя инновационной по тем временам электронной биржи NASDAQ, придуманной изначально как раз для торговли акциями этого фонда, Бернарда Л. Мэдоффa, «обещанные» активы клиентов которого прокуратура оценила в 64.8 млрд. долл. (суд, правда, насчитал лишь 17 млрд., из которых Мэдоффу предстоит заработать шитьем рукавиц и выплатить пострадавшим 7.2 млрд. долл. за 150 лет отсидки). Пирамидальный характер фонда Мэдоффа, работавшего на рынке с 1960, и стабильно показывавшего относительно умеренную доходность в 10% год., вскрылся осенью 2008. Тогда крупные клиенты, пострадавшие от финансового кризиса, попытались изъять 7 млрд. долл. (фактические активы фонда на тот момент составляли лишь 826 млн.).
Правда, расследования велись уже с 2000, а в июне 2005 Мэдофф был на грани банкротства. Перед закрытием фирма выплатила сотрудникам бонусы, о чем сыновьями Мэдоффа, также работавшими в фирме, было заявлено куда следует (один из них через 2 года повесился). Сам Мэдофф не сдал никого, подписал отказ от обвинительного заключения и согласие с предложенными обвинением 150 годами, и отправился отсиживать их один. (Но расследование продолжалось, потом были и другие посаженные работники фонда, и еще самоубийства, естественно - куда ж без них в индустрии).
4. Модель, описывающая движение цен Bt в пузыре, включает в себя такие параметры, как (условное) распределение вероятностей цен спустя некоторое время (день, час, месяц), при информации, доступной сейчас, и депозитную ставку rt с добавкой за риск инвестиций, доходность которых вероятностна. В простейшем случае развитие пузыря удовлетворяет условию Bt = Et (Bt+1) / (1+ rt), выражающем равновесие на данном рынке.
Простейшее удовлетворяющее этому условию нетривиальное распределение вероятностей ожидаемой цены спустя некоторое время – 0, с вероятностью pt пузырь лопнет в течение этого периода, и Вt*(1+ rt) / (1-pt) с вероятностью (1- pt), т.е. экспонента, растущая темпом значительно более крутым, чем ставка по депозиту, если вероятность, что пузырь может лопнуть, велика [1].
Поскольку присутствуя в пузыре, держатель актива покупает «доходность, взвешенную по уровням риска», то его поведение может показаться рациональным - таким же, как при формировании портфеля из обычных, «не пузырящихся» активов. Проблема в том, что каждый пузырь представляет собой достаточно уникальное явление, и говорить о вероятностях и мат. ожидании цены можно лишь в смысле «вероятности суждений» (байесовской), а не обычной («частотной») вероятности. Так что отличить рациональный пузырь от иррационального, и от других проявлений волатильности, пожалуй, и впрямь не получится, пока он не лопнет.
В учебниках также весьма популярен разбор модели, когда «пузырящимся» активом являются деньги, а их «ценой» - величина, обратная индексу цен. В этом случае инфляция либо стабилизируется на некотором уровне, либо будет неограниченно расти (случай гиперинфляции) в зависимости от сочетания 2-х параметров: (а) потребности правительства в сеньораже (эмиссионном доходе); (б) зависимости скорости обращения денег («бегства от денег») от инфляционных (эмиссионных) ожиданий. При определенных предположениях о влиянии ожиданий здесь также могут надуваться пузыри, вызывающие не эмиссионную инфляцию (небольшое кол-во ссылок тут). И на этом все о пузырях, дальше займемся пирамидами.
5. Достаточно наглядная и удобная для исследования модель [2], описывающая развитие пирамиды с фактической стоимостью активов St, (чтобы не распугать читателя интегралами, я перепишу эту модель из исходной статьи в более удобном для восприятия виде с дискретным временем). Она включает в себя следующие 4 параметра: обещаемую, обычно нереально высокую процентную ставку rp; нормальную депозитную ставку, по которой фонд может инвестировать собранные деньги rn (для пирамиды характерно, что rp > rn); скорость, с которой новые депозиты накапливаются в фонде ri; скорость вывода денег участниками rw. При определённых соотношениях между ними пирамида может устойчиво функционировать неограниченно долго, при других – быстро разрушится, а при третьих – может быть спасена с помощью процедуры bailout’а (временной до капитализации), после чего станет устойчивой. Рассмотрим их.
Если в начальный момент «обещанная» к выплате сумма депозитов равна K, а приток денег в период h равен sh = s * (1 + ri)h (в дальнейшем мы разберем также случай «внезапной остановки» притока депозитов в фонд, но пока ограничимся простейшим предположением), то вывод денег из фонда в период t будет:
Wt = rw *(K * (1 + rp – rw)t + ∑h=1 t-1 s * (1 + ri) t –h * (1 + rp – rw)h).
C учетом этого динамика фактических активов фонда, включая доход от их размещения по нормальной, «непирамидальной» ставке, описывается разностным уравнением:
St+1 = (1 + rn) *St + s*(1 + ri)t * (1 - r * (∑h=1 t-1 (1 + rp – ri – rw)h ) - rw (K * (1 + rp – rw)t.
Если просуммировать тут геометрическую прогрессию (не будем уже загромождать дальше формулами запись), то получим уравнение вида 4 отсюда. Его решение представляет собой линейную комбинацию трех экспонент, с тремя показателями темпов роста, и тремя – весов. Темп прироста у одной из экспонент будет rn- «нормальный» процент, под который фонд может разместить собранные деньги; остальные 5 параметров элементарно, но громоздко выражаются через 7 коэффициентов, описывающих пирамиду (4 темпа прироста /вывода / «нормальный» / «обещаемый» процент и 3 начальных значения: K, s и собственный капитал основателя пирамиды С = S0 – K.
В 2 показано, что в зависимости от сочетаний этих параметров движение St активов фонда имеет 0, 1 или 2 нуля при положительных значениях t. Первый случай описывает «устойчивую» пирамиду, которая может функционировать сколь угодно долго, второй – коллапс, и третий - пирамиду с возможностью «спасения».
В одной из следующих записей мы рассмотрим сочетания параметров, приводящих к одному из этих трех типов пирамиды, и попытаемся численно смоделировать развитие какой-нибудь известной пирамиды, скажем, МММ с отрицательным rn - когда активы никуда не размещаются, а в определенной доле тратятся на рекламу. (Эта запись уже и так великовата.)
Ссылки:
Blanchard, O. and Watson, M., 1982. Bubbles, Rational Expectations, and Financial Markets, in Paul Wachter (ed.) Crises in the Economic and Financial Structure. Lexington, MA: Lexington Books, pp. 295-315. pdf
Marc Artzrouni, 2. April 2009. The mathematics of Ponzi schemes. Department of Mathematics - University of Pau. pdf
Blanchard, O. and Watson, M., 1982. Bubbles, Rational Expectations, and Financial Markets, in Paul Wachter (ed.) Crises in the Economic and Financial Structure. Lexington, MA: Lexington Books, pp. 295-315. pdf
Marc Artzrouni, 2. April 2009. The mathematics of Ponzi schemes. Department of Mathematics - University of Pau. pdf
Не является индивидуальной инвестиционной рекомендацией | При копировании ссылка обязательна | Нашли ошибку - выделить и нажать Ctrl+Enter | Жалоба


