19 августа 2015 QuantAlgos
Вступление
Успех многих торговых алгоритмов зависит от качества предсказаний движения цены актива. Предсказания цены отдельной акции в общем случае менее точно, чем предсказание значения портфеля активов. Классической стратегией, которая использует совместное поведение двух активов, является парный трейдинг, где портфель состоит из линейной комбинации этих активов. Для примера, это могут быть две акции, чей спред, представляющий собой разницу их цен, демонстрирует особый паттерн, отклонения от которого носят временный характер. Алгоритм парного трейдинга получает прибыль от ставки на тот факт, что отклонения спреда возвратятся к их историческому или предсказуемому уровню.
В данной работе мы создадим оптимальную стратегию, в которой агент открывает позиции в n коинтегрированных активах. Цель стратегии - получение прибыли от структурной зависимости в динамике их цен . Мы предполагаем, что активы коинтегрированы и создадим алгоритмическую торговую стратегию, где инвестор максимизирует ожидаемую функцию владения ( то есть вложенные и наличные средства). Мы выведем отдельную закрытую формулу для оптимальной (динамической) инвестиционной стратегии и покажем, что она учитывает коинтеграционный фактор. Далее, мы используем данные торгов с биржи Nasdaq для калибровки модели и проведем симуляцию, чтобы продемонстрировать, насколько стратегия производительна, в случае, когда инвестор открывает позиции в трех активах : Google, Facebook и Amazon.
Мы предполагаем, что дрифт в приращениях цен активов состоит из компонента, присущего только данному активу, и общего компонента для всех используемых активов. Общий компонент, который мы называем краткосрочной альфа, представляет собой процесс возврата к среднему с нулевым средним, являющийся естественным источником прибыли в торговой стратегии - он определяет прибыль от краткосрочных инвестиционных возможностей для коллекции активов.
Коинтегрированные логарифмы цен с краткосрочной альфа
Предположим, что дрифт в приращениях цен активов состоит из особого и общего компонентов. Особый компонент есть результат факторов, влияющих только на каждый отдельный актив, и общий компонент - результат индустриального или секторального набора факторов, которые влияют на всю коллекцию используемых активов. Таким образом, у нас есть коллекция активов, чей вектор цен обозначим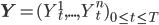 , который удовлетворяет системе дифференциальных уравнений:
, который удовлетворяет системе дифференциальных уравнений:
\begin{equation}\frac{dY_t^k}{Y_t^k}=(\nu_k+\delta_k\alpha_t)dt+\sum_{i=1}^n\sigma_{ki}dW_t^i\end{equation}
где особый компонент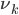 является константой, и общий компонент :
является константой, и общий компонент :
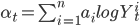 ,
,
где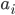 - константы, и
- константы, и 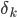 - специальная константа , которая показывает, как общий компонент влияет на каждый актив.
- специальная константа , которая показывает, как общий компонент влияет на каждый актив.
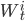 - стандартные Броуновские движения, независящие друг от друга, собранные в вектор
- стандартные Броуновские движения, независящие друг от друга, собранные в вектор 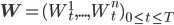 , и
, и 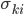 - неотрицательные константы. Мгновенную ковариацию между активами i и j можно определить как:
- неотрицательные константы. Мгновенную ковариацию между активами i и j можно определить как:
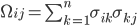
Далее, обозначим матрицу, чьими элементами являются
матрицу, чьими элементами являются 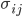 , представляющую собой разложение Холецкого мгновенной дисперсионно-ковариационной матрицы
, представляющую собой разложение Холецкого мгновенной дисперсионно-ковариационной матрицы 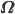 , таким образом
, таким образом 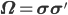 , где ' обозначает оператор транспонирования. Предположим, что нет дополнительных степеней свободы, так что
, где ' обозначает оператор транспонирования. Предположим, что нет дополнительных степеней свободы, так что  является обратимой.
является обратимой.
Покажем, что ведет себя как фактор коинтеграции. Когда
ведет себя как фактор коинтеграции. Когда 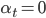 все активы являются геометрическими броуновскими движениями с дрифтом
все активы являются геометрическими броуновскими движениями с дрифтом 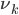 . В общем случае, на рынках акций,
. В общем случае, на рынках акций,  будет ненулевой и отклонения от ее долгосрочного или предсказуемого уровня быстро нивелируются. Такое поведение этого компонента мы назовем краткосрочной альфа, и она представляет собой отклонения от ожидаемого приращения активов.
будет ненулевой и отклонения от ее долгосрочного или предсказуемого уровня быстро нивелируются. Такое поведение этого компонента мы назовем краткосрочной альфа, и она представляет собой отклонения от ожидаемого приращения активов.
Докажем, что является коинтеграционным фактором, продемонстрировав, что это, несомненно, процесс возврата к среднему. Во-первых отметим, что логарифмы цен удовлетворяют дифференциальному уравнению:
является коинтеграционным фактором, продемонстрировав, что это, несомненно, процесс возврата к среднему. Во-первых отметим, что логарифмы цен удовлетворяют дифференциальному уравнению:
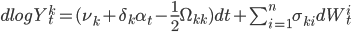 ,
,
которое мы используем для вычисления дифференциала :
:
\begin{equation}d\alpha_t=\sum_{k=1}^n a_k(\nu_k+\delta_k\alpha_t-\frac{1}{2}\Omega_{kk})dt+\sum_{k=1}^n a_k\sum_{i=1}^n\sigma_{ki}dW_t^i\end{equation}
Таким образом, мы можем записать компонент краткосрочной альфы как процесс возврата к среднему:

Здесь, оператор Tr() обозначает след матрицы, и А=diag(a) - диагональная матрица, чья диагональ состоит из а. Для уверенности, что модель действительно описывает процесс возврата к среднему, мы предположим, что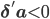 - и это мы увидим в результатах калибровки модели на реальных данных с биржи Nasdaq.
- и это мы увидим в результатах калибровки модели на реальных данных с биржи Nasdaq.
Рассматривая динамику (2), мы можем видеть, что возвращается к среднему с частотой, которая зависит от различной степени воздействия, какую оказывает на каждый актив (через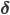 ), а также от силы вклада логарифма цены актива в саму
), а также от силы вклада логарифма цены актива в саму  (через а). Уровень возврата к среднему
(через а). Уровень возврата к среднему 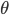 зависит от отношения волатильности к воздействию каждого компонента на общий дрифт активов и на дрифт каждого актива.
зависит от отношения волатильности к воздействию каждого компонента на общий дрифт активов и на дрифт каждого актива.
Альтернативное представление модели можно вывести, поместив выражение для непосредственно в дифференциальное уравнение для
непосредственно в дифференциальное уравнение для 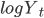 . В этом случае, мы получаем:
. В этом случае, мы получаем:
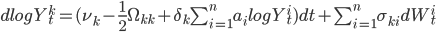 ,
,
и если мы обозначим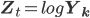 , где логарифм применен к каждому компоненту, то
, где логарифм применен к каждому компоненту, то
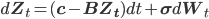 ,
,
где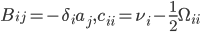 .
.
В этом представлении мы видим, что логарифм цены представляет собой векторно-авторегрессивную модель 1 порядка (VAR(1)). Отметим здесь, что B - вырожденная матрица. которая имеет одно положительное собственное значение, соответственно единственному фактору коинтеграции, который мы заложили в модель.
В следующей части мы найдем оптимальное динамическое уравнение распределения активов для нашего портфеля в закрытой форме, а затем продемонстрируем, как использовать выведенные формулы на практике, на примере портфеля из трех акций.
Успех многих торговых алгоритмов зависит от качества предсказаний движения цены актива. Предсказания цены отдельной акции в общем случае менее точно, чем предсказание значения портфеля активов. Классической стратегией, которая использует совместное поведение двух активов, является парный трейдинг, где портфель состоит из линейной комбинации этих активов. Для примера, это могут быть две акции, чей спред, представляющий собой разницу их цен, демонстрирует особый паттерн, отклонения от которого носят временный характер. Алгоритм парного трейдинга получает прибыль от ставки на тот факт, что отклонения спреда возвратятся к их историческому или предсказуемому уровню.
В данной работе мы создадим оптимальную стратегию, в которой агент открывает позиции в n коинтегрированных активах. Цель стратегии - получение прибыли от структурной зависимости в динамике их цен . Мы предполагаем, что активы коинтегрированы и создадим алгоритмическую торговую стратегию, где инвестор максимизирует ожидаемую функцию владения ( то есть вложенные и наличные средства). Мы выведем отдельную закрытую формулу для оптимальной (динамической) инвестиционной стратегии и покажем, что она учитывает коинтеграционный фактор. Далее, мы используем данные торгов с биржи Nasdaq для калибровки модели и проведем симуляцию, чтобы продемонстрировать, насколько стратегия производительна, в случае, когда инвестор открывает позиции в трех активах : Google, Facebook и Amazon.
Мы предполагаем, что дрифт в приращениях цен активов состоит из компонента, присущего только данному активу, и общего компонента для всех используемых активов. Общий компонент, который мы называем краткосрочной альфа, представляет собой процесс возврата к среднему с нулевым средним, являющийся естественным источником прибыли в торговой стратегии - он определяет прибыль от краткосрочных инвестиционных возможностей для коллекции активов.
Коинтегрированные логарифмы цен с краткосрочной альфа
Предположим, что дрифт в приращениях цен активов состоит из особого и общего компонентов. Особый компонент есть результат факторов, влияющих только на каждый отдельный актив, и общий компонент - результат индустриального или секторального набора факторов, которые влияют на всю коллекцию используемых активов. Таким образом, у нас есть коллекция активов, чей вектор цен обозначим
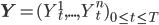 , который удовлетворяет системе дифференциальных уравнений:
, который удовлетворяет системе дифференциальных уравнений: \begin{equation}\frac{dY_t^k}{Y_t^k}=(\nu_k+\delta_k\alpha_t)dt+\sum_{i=1}^n\sigma_{ki}dW_t^i\end{equation}
где особый компонент
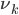 является константой, и общий компонент :
является константой, и общий компонент : 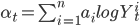 ,
, где
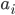 - константы, и
- константы, и 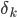 - специальная константа , которая показывает, как общий компонент влияет на каждый актив.
- специальная константа , которая показывает, как общий компонент влияет на каждый актив. 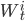 - стандартные Броуновские движения, независящие друг от друга, собранные в вектор
- стандартные Броуновские движения, независящие друг от друга, собранные в вектор 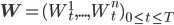 , и
, и 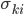 - неотрицательные константы. Мгновенную ковариацию между активами i и j можно определить как:
- неотрицательные константы. Мгновенную ковариацию между активами i и j можно определить как: 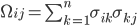
Далее, обозначим
 матрицу, чьими элементами являются
матрицу, чьими элементами являются 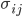 , представляющую собой разложение Холецкого мгновенной дисперсионно-ковариационной матрицы
, представляющую собой разложение Холецкого мгновенной дисперсионно-ковариационной матрицы 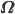 , таким образом
, таким образом 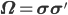 , где ' обозначает оператор транспонирования. Предположим, что нет дополнительных степеней свободы, так что
, где ' обозначает оператор транспонирования. Предположим, что нет дополнительных степеней свободы, так что  является обратимой.
является обратимой. Покажем, что
 ведет себя как фактор коинтеграции. Когда
ведет себя как фактор коинтеграции. Когда 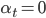 все активы являются геометрическими броуновскими движениями с дрифтом
все активы являются геометрическими броуновскими движениями с дрифтом 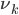 . В общем случае, на рынках акций,
. В общем случае, на рынках акций,  будет ненулевой и отклонения от ее долгосрочного или предсказуемого уровня быстро нивелируются. Такое поведение этого компонента мы назовем краткосрочной альфа, и она представляет собой отклонения от ожидаемого приращения активов.
будет ненулевой и отклонения от ее долгосрочного или предсказуемого уровня быстро нивелируются. Такое поведение этого компонента мы назовем краткосрочной альфа, и она представляет собой отклонения от ожидаемого приращения активов. Докажем, что
 является коинтеграционным фактором, продемонстрировав, что это, несомненно, процесс возврата к среднему. Во-первых отметим, что логарифмы цен удовлетворяют дифференциальному уравнению:
является коинтеграционным фактором, продемонстрировав, что это, несомненно, процесс возврата к среднему. Во-первых отметим, что логарифмы цен удовлетворяют дифференциальному уравнению: 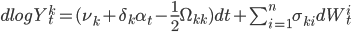 ,
, которое мы используем для вычисления дифференциала
 :
: \begin{equation}d\alpha_t=\sum_{k=1}^n a_k(\nu_k+\delta_k\alpha_t-\frac{1}{2}\Omega_{kk})dt+\sum_{k=1}^n a_k\sum_{i=1}^n\sigma_{ki}dW_t^i\end{equation}
Таким образом, мы можем записать компонент краткосрочной альфы как процесс возврата к среднему:

Здесь, оператор Tr() обозначает след матрицы, и А=diag(a) - диагональная матрица, чья диагональ состоит из а. Для уверенности, что модель действительно описывает процесс возврата к среднему, мы предположим, что
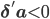 - и это мы увидим в результатах калибровки модели на реальных данных с биржи Nasdaq.
- и это мы увидим в результатах калибровки модели на реальных данных с биржи Nasdaq. Рассматривая динамику (2), мы можем видеть, что возвращается к среднему с частотой, которая зависит от различной степени воздействия, какую оказывает на каждый актив (через
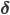 ), а также от силы вклада логарифма цены актива в саму
), а также от силы вклада логарифма цены актива в саму  (через а). Уровень возврата к среднему
(через а). Уровень возврата к среднему 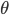 зависит от отношения волатильности к воздействию каждого компонента на общий дрифт активов и на дрифт каждого актива.
зависит от отношения волатильности к воздействию каждого компонента на общий дрифт активов и на дрифт каждого актива. Альтернативное представление модели можно вывести, поместив выражение для
 непосредственно в дифференциальное уравнение для
непосредственно в дифференциальное уравнение для 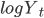 . В этом случае, мы получаем:
. В этом случае, мы получаем: 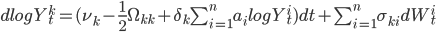 ,
, и если мы обозначим
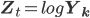 , где логарифм применен к каждому компоненту, то
, где логарифм применен к каждому компоненту, то 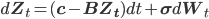 ,
, где
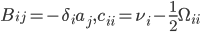 .
. В этом представлении мы видим, что логарифм цены представляет собой векторно-авторегрессивную модель 1 порядка (VAR(1)). Отметим здесь, что B - вырожденная матрица. которая имеет одно положительное собственное значение, соответственно единственному фактору коинтеграции, который мы заложили в модель.
В следующей части мы найдем оптимальное динамическое уравнение распределения активов для нашего портфеля в закрытой форме, а затем продемонстрируем, как использовать выведенные формулы на практике, на примере портфеля из трех акций.
Не является индивидуальной инвестиционной рекомендацией | При копировании ссылка обязательна | Нашли ошибку - выделить и нажать Ctrl+Enter | Жалоба

