8 апреля 2019 smart-lab.ru

Наш ответ Талебу на его опционную формулу
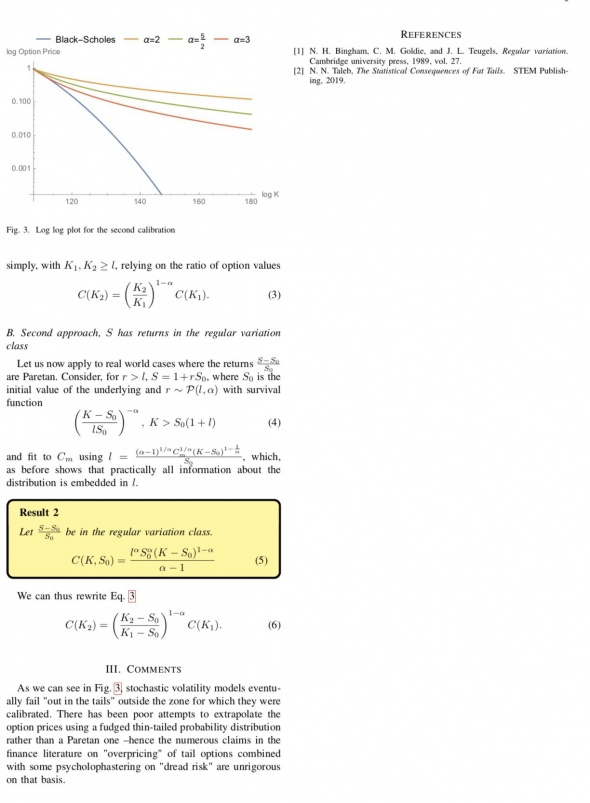
Когда имеешь график функции, такой как опционные цены, то можно подобрать функцию которая ляжет на этот график. У меня есть целая коллекция таких функций. Но я вам хочу представить функцию, которой можно дать объяснения и потом долго доказывать, что она правильная.
В природе много различных процессов, которые математически описываются одними и теми же математическими формулами. Возьмем за основу процесс, график которого очень схож с прайсингом опционов.

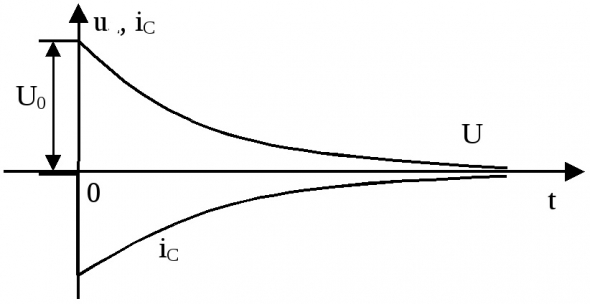
Такой очень знакомый график для опционных цен.
Теперь начальное напряжение заменим на риск на центральном страйке. По сути, цена опциона на центральном страйке соответствует риску проданного опциона. Предположим, что риск проданного опциона уменьшается по тем же законам, как происходит разряд конденсатора. Только в место времени у нас расстояние от центрального страйка.
Обозначим риск через Q, а расстояние от центрального страйка через Х.
Еще у нас в формуле есть параметр системы (R*C). В нашей опционной системе основной параметр это риск. То есть, (R*C) логично заменить на Q. Но надо учитывать, что наша опционная система не стабильна и риск может сильно меняться со временем. Поэтому (R*C) мы заменим на двойной риск (2*Q). В итоге получилась красивая формула:
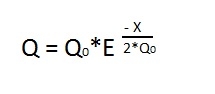
Поскольку, цена опциона соответствует риску, то Q мы принимаем за искомую цену опциона в пунктах на Расстоянии Х ( в пунктах) от центрального страйка. При этом цена на центральном страйке равна Q0 (в пунктах).
Посмотрим, как ляжет наша функция на рынок. Ложится она примерно так:

И окончательный вариант, через который считаются путы, колы и опционы в деньгах выглядит так:
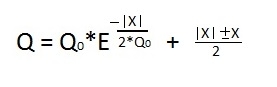
Думайте, наслаждайтесь, вставляйте всякие коэффициенты для наклона улыбки, для учета процентной ставки. Пробуйте по другому оценить риск нестабильности системы.
Не является индивидуальной инвестиционной рекомендацией | При копировании ссылка обязательна | Нашли ошибку - выделить и нажать Ctrl+Enter | Жалоба

