7 марта 2020 smart-lab.ru Логунов Евгений
В этой статье я рассмотрю одно из ограничений, которое должно выполняться для «хорошей» модели улыбки волатильности.
Основная идея
Допустим, у нас есть модель улыбки волатильности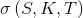 , с использованием которой мы оцениваем европейские опционы типа «call»
, с использованием которой мы оцениваем европейские опционы типа «call» 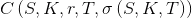 и и «put»
и и «put» 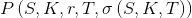 по формуле Блэка-Шоулза. Далее для краткости я буду опускать некоторые аргументы в последних двух выражениях, уделяя внимание лишь тем аргументам, которые важны.
по формуле Блэка-Шоулза. Далее для краткости я буду опускать некоторые аргументы в последних двух выражениях, уделяя внимание лишь тем аргументам, которые важны.
В работе [1] (см. список литературы) было предложено следующее ограничение на улыбку волатильности: она должна быть такова, чтобы стоимость колл-спредов и пут-спредов была неотрицательна, т.е. для любой пары страйков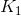 и и
и и 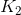 таких что
таких что  должно выполняться
должно выполняться 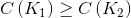 и
и  . В работе [2] требование для путов было усилено до
. В работе [2] требование для путов было усилено до 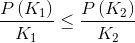 .
.
Продифференцируем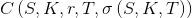 по
по 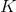 :
: 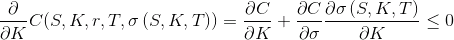 .
.
Отсюда получим верхнюю границу для наклона улыбки волатильности: .
.
Аналогичным образом может быть получена нижняя граница; в этом случае дифференцировать следует или
или 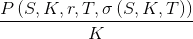 , для получения усиленной в [2] границы.
, для получения усиленной в [2] границы.
Воспользуемся составляющими формулы Блэка-Шоулза, чтобы в явном виде записать выражения для верхней и нижней границ наклона улыбки волатильности: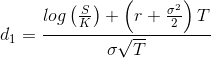 ,
, 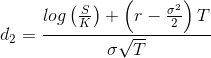 . Также определим функцию
. Также определим функцию 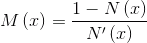 (известную как Mills ratio), где
(известную как Mills ratio), где  — PDF стандартного нормального распределения,
— PDF стандартного нормального распределения, 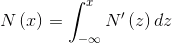 — CDF стандартного нормального распределения.
— CDF стандартного нормального распределения.
Согласно Hodges [1], наклон улыбки в каждой точке должен удовлетворять: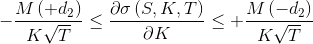 .
.
Усиленное требование, согласно Gatheral [2] и Carr, Wu [3], имеет вид: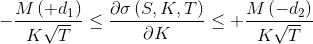 .
.
Небольшая иллюстрация
Выбрав некоторое значение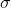 в точке
в точке 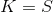 можно рассмотреть случай, когда наклон улыбки равен одной из границ, и численно проинтегрировать полученные дифференциальные уравнения. В результате получим границы, за которые не должна выходить улыбка волатильности при заданной волатильности at-the-money:
можно рассмотреть случай, когда наклон улыбки равен одной из границ, и численно проинтегрировать полученные дифференциальные уравнения. В результате получим границы, за которые не должна выходить улыбка волатильности при заданной волатильности at-the-money:
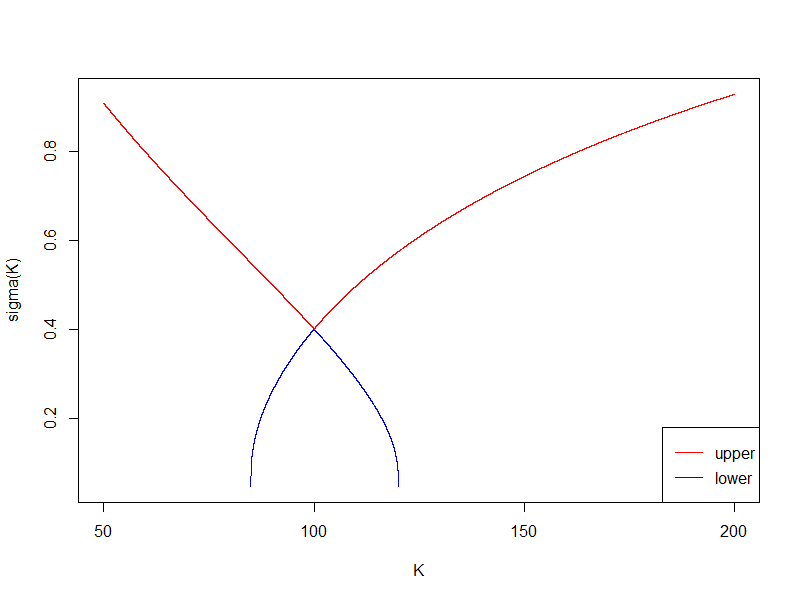
Т.е. края улыбки не могут быть задраны произвольно высоко, как и не может быть произвольным наклон на центре. Подумайте над этим, применительно к вашей любимой модели улыбки волатильности и вашему любимому софту.
Быстрый способ обнаружения арбитража
Пусть даны две котировки в терминах implied volatility: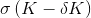 и
и 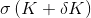 .
.
Обозначим оценку верхней границы наклона улыбки волатильности в точке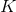 как
как  .
.
Арбитраж возможен, если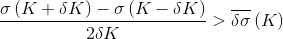 .
.
Оценка производной улыбки, стоящая в левой части неравенства, разумеется, является приближенной. Думайте, прежде чем применять.
Немного кода на R
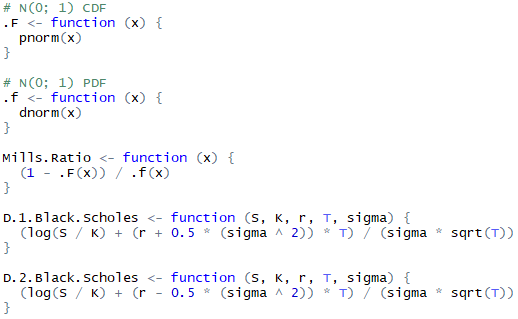

Литература
1. Hardy M. Hodges «Arbitrage Bounds of the Implied Volatility Strike and Term Structures of European-Style Options» / The Journal of Derivatives, 1996, Volume 3, Issue 4, p. 23-35
2. Jim Gatheral «The volatility skew: Arbitrage constraints and asymptotic behaviour» / Merrill Lynch, 1999
3. Peter Carr, Liuren Wu «The finite moment logstable process and option pricing» / Journal of Finance, 2002
4. Roger W. Lee «Implied Volatility: Statics, Dynamics, and Probabilistic Interpretation» / November 22, 2002 / Recent Advances in Applied Probability, Springer 2004
5. Michael Paul Veran Roper «Implied Volatility: General Properties and Asymptotics» (PhD thesis) / October 14, 2009
Основная идея
Допустим, у нас есть модель улыбки волатильности
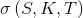 , с использованием которой мы оцениваем европейские опционы типа «call»
, с использованием которой мы оцениваем европейские опционы типа «call» 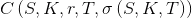 и и «put»
и и «put» 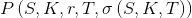 по формуле Блэка-Шоулза. Далее для краткости я буду опускать некоторые аргументы в последних двух выражениях, уделяя внимание лишь тем аргументам, которые важны.
по формуле Блэка-Шоулза. Далее для краткости я буду опускать некоторые аргументы в последних двух выражениях, уделяя внимание лишь тем аргументам, которые важны.В работе [1] (см. список литературы) было предложено следующее ограничение на улыбку волатильности: она должна быть такова, чтобы стоимость колл-спредов и пут-спредов была неотрицательна, т.е. для любой пары страйков
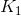 и и
и и 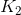 таких что
таких что  должно выполняться
должно выполняться 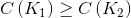 и
и  . В работе [2] требование для путов было усилено до
. В работе [2] требование для путов было усилено до 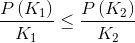 .
.Продифференцируем
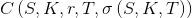 по
по 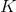 :
: 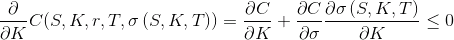
Отсюда получим верхнюю границу для наклона улыбки волатильности:
 .
.Аналогичным образом может быть получена нижняя граница; в этом случае дифференцировать следует
 или
или 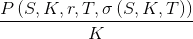 , для получения усиленной в [2] границы.
, для получения усиленной в [2] границы.Воспользуемся составляющими формулы Блэка-Шоулза, чтобы в явном виде записать выражения для верхней и нижней границ наклона улыбки волатильности:
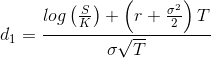 ,
, 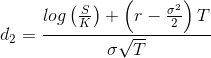 . Также определим функцию
. Также определим функцию 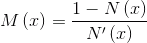 (известную как Mills ratio), где
(известную как Mills ratio), где  — PDF стандартного нормального распределения,
— PDF стандартного нормального распределения, 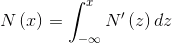 — CDF стандартного нормального распределения.
— CDF стандартного нормального распределения.Согласно Hodges [1], наклон улыбки в каждой точке должен удовлетворять:
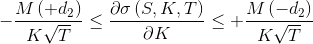 .
.Усиленное требование, согласно Gatheral [2] и Carr, Wu [3], имеет вид:
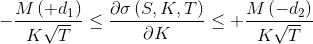 .
.Небольшая иллюстрация
Выбрав некоторое значение
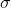 в точке
в точке 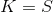 можно рассмотреть случай, когда наклон улыбки равен одной из границ, и численно проинтегрировать полученные дифференциальные уравнения. В результате получим границы, за которые не должна выходить улыбка волатильности при заданной волатильности at-the-money:
можно рассмотреть случай, когда наклон улыбки равен одной из границ, и численно проинтегрировать полученные дифференциальные уравнения. В результате получим границы, за которые не должна выходить улыбка волатильности при заданной волатильности at-the-money:
Т.е. края улыбки не могут быть задраны произвольно высоко, как и не может быть произвольным наклон на центре. Подумайте над этим, применительно к вашей любимой модели улыбки волатильности и вашему любимому софту.
Быстрый способ обнаружения арбитража
Пусть даны две котировки в терминах implied volatility:
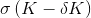 и
и 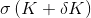 .
.Обозначим оценку верхней границы наклона улыбки волатильности в точке
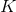 как
как  .
.Арбитраж возможен, если
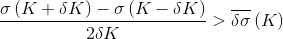 .
.Оценка производной улыбки, стоящая в левой части неравенства, разумеется, является приближенной. Думайте, прежде чем применять.
Немного кода на R


Литература
1. Hardy M. Hodges «Arbitrage Bounds of the Implied Volatility Strike and Term Structures of European-Style Options» / The Journal of Derivatives, 1996, Volume 3, Issue 4, p. 23-35
2. Jim Gatheral «The volatility skew: Arbitrage constraints and asymptotic behaviour» / Merrill Lynch, 1999
3. Peter Carr, Liuren Wu «The finite moment logstable process and option pricing» / Journal of Finance, 2002
4. Roger W. Lee «Implied Volatility: Statics, Dynamics, and Probabilistic Interpretation» / November 22, 2002 / Recent Advances in Applied Probability, Springer 2004
5. Michael Paul Veran Roper «Implied Volatility: General Properties and Asymptotics» (PhD thesis) / October 14, 2009
Не является индивидуальной инвестиционной рекомендацией | При копировании ссылка обязательна | Нашли ошибку - выделить и нажать Ctrl+Enter | Жалоба

