2 октября 2019 smart-lab.ru
Сегодня мы будем выступать в качестве поставщика бесконечной ликвидности по опционам. То есть мы будем безотказно играть в игру с нулевой суммой так, чтобы, как минимум, не проиграть, а это возможно только в том случае, если мы будем продавать и покупать волатильность по цене, соответствующей седловой точке в игре покупателя и продавца, то есть по цене GTO (game theory optimal). Иными словами, мы будем заниматься непосредственно pricing'ом опционов, назначая цены put'ам и call'ам, таким образом, чтобы ни одна стратегия и ни один набор случайных, стохастических стратегий не мог получить положительное преимущество при игре с нами.
Чтобы назначать цену волатильности, для начала, не плохо было бы принять какую-либо модель волатильности. Например, это может быть модель случайного процесса, подчинённого логистическому распределению:
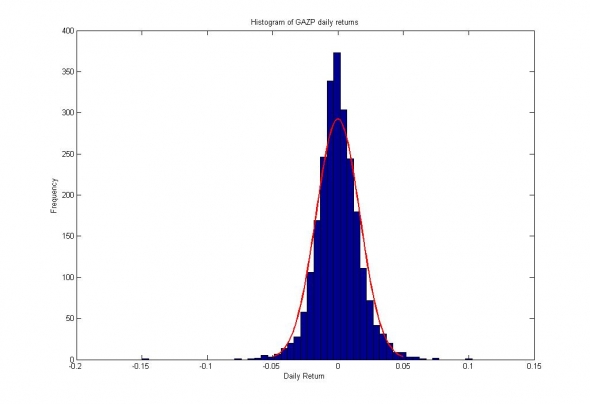
Рис.1. Распределение логарифмических приращений цен акций ПАО Газпром и их аппроксимация логистическим распределением.
или распределению Лапласа:
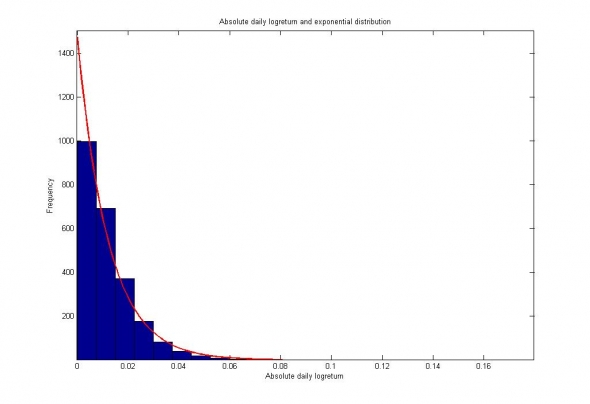
Рис. 2. Распределение абсолютных значений логарифмических приращений цен акций ПАО Газпром и их апроксимация экспоненциальным распределением.
Поскольку нам ближе безарбитражные процессы с неравномерным распределением средней мощности (волатильности) во времени (см. «Кому улыбается волатильность»), мы остановимся на втором варианте.
Экспоненциальное распределение это распределение одного параметра — m=sigma - который нам нужно оценить во времени, то есть, принимая во внимание эффект кластеризации волатильности, нам нужно оценить не только форму локального распределения приращений, но и его ширину. Иными словами, помимо самой функции распределения приращений, обладающей некоторой волатильностью (шириной), мы будем ещё учитывать и изменчивость этой волатильности во времени, то есть, непосредственно, волатильность волатильности.
Для этого мы будем пользоваться автоматически настраиваемой EWMA — 40 ( относится к классу ARCH — 40) моделью.
Исходный алгоритм принимает на вход временной ряд из последних 40 логарифмических приращений и последовательно производит действия:
Оценивает параметры EWMA модели
Строит саму модель и оценивает её ошибку
Исходя из полученной модели волатильности и ошибки этой модели на IS выборке оценивает будущую волатильность и распределение ошибок будущей волатильности.
Принципиально, данная автонастраиваемая модель практически не зависит от выбора окна, но, тем не менее, даёт наилучшие результаты на окне равным двум последним месяцам (40).
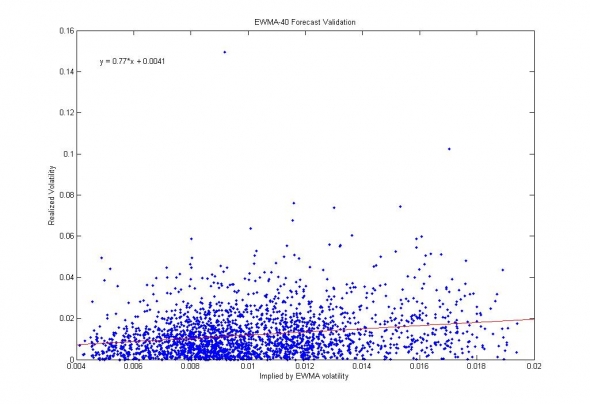
Рис. 3. Результаты прогнозирования волатильности автонастраиваемой EWMA-40 моделью. Корреляция прогноза и реализации — 77%.
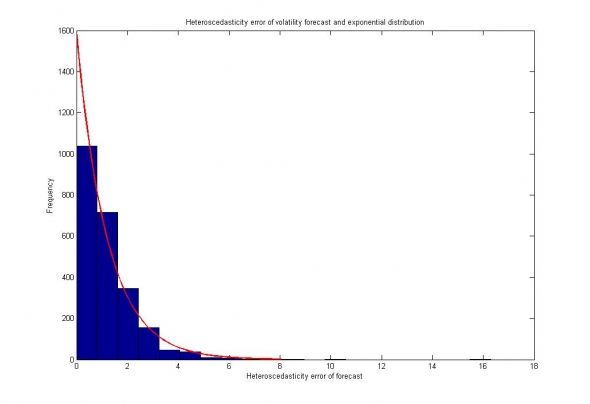
Рис. 4. Гетероскедастичная ошибка прогноза волатильности и его апроксимация распределением Лапласа (экспоненциальным).
Как видно, гетероскедастичная ошибка данной модели повторяет исходное распределение ряда, что говорит о том, что мы определили волатильность правильно, то есть, спрогнозировали непосредственно саму волатильность (ширину распределения), а не что-либо другое.
Теперь, из прогноза волатильности и его гетероскедастичной ошибки, нам осталось только получить распределение логарифмических приращений цен базового актива на ближайшее будущее и можно приступить к расчету цен опционов. Но, такой подход был бы слишком… непрофессионален, поэтому мы зашифруем простые и понятные результаты численного интегрирования экспоненциального распределения в сложную форму улыбки предполагаемой волатильности Блэка-Шоулза, павно перетекающей в дельта-хедж по Корнеру-Фишеру, а чтобы было ещё надёжней — построим не просто улыбку, а рельефную поверхность этой улыбки, протекающей в пространственно-временном континууме, свёрнутом в бублик суперструны.
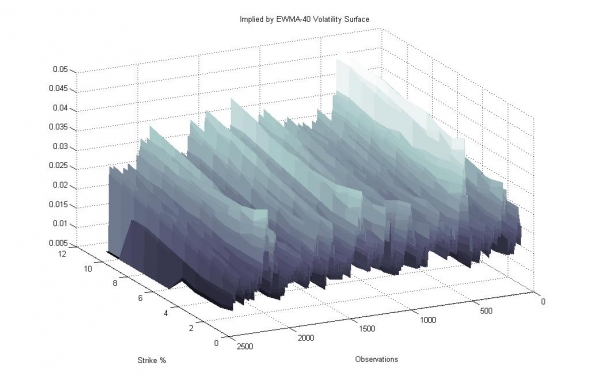
Рис. 5. Полученная поверхность IV auto-EWMA-40 моделью по Smile Theory Optimal.
Для того, чтобы убедиться в отсутствии misspricing, то есть соответствии STO цен GTO-оптимальным, безорбитражным ценам, проведём симуляцию продажи опционов квалифицированным инвесторам и рассмотрим их результирующую прибыль:
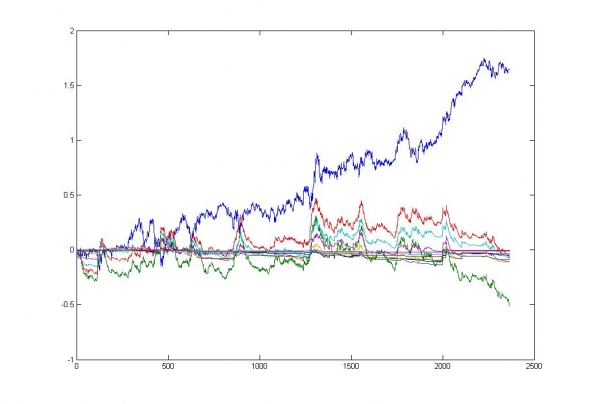
Рис. 6. Симуляция продажи стрэддлов по различным страйкам на БА — TATN. Нормированное уклонение финансового результата от нуля лежит в интервале от -0.8 до -0.16 сигма.
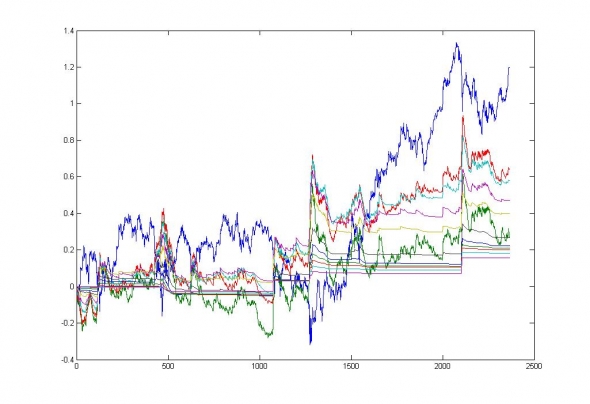
Рис. 7. Симуляция продажи стрэддлов по различным страйкам на БА — SBER. Нормированное уклонение финансового результата от нуля лежит в интервале от 0.4 до 1.4 сигма.
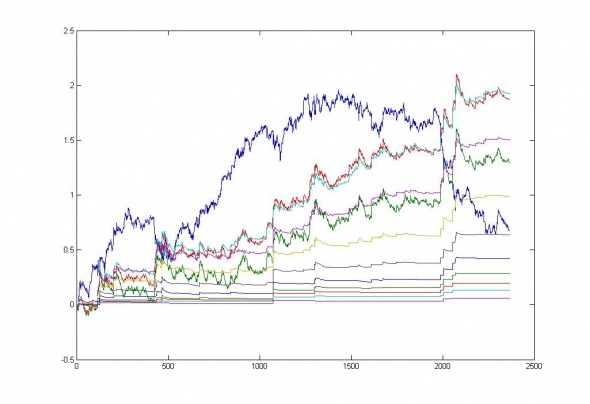
Рис. 8. Симуляция продажи стрэддлов по различным страйкам на БА — MGNT. Нормированное уклонение финансового результата от нуля лежит в интервале от 1.9 до 4.24 сигма. Что, для распределений с «тяжелыми хвостами», соответствующих стратегиям покупки стэдллов — более чем нормально.
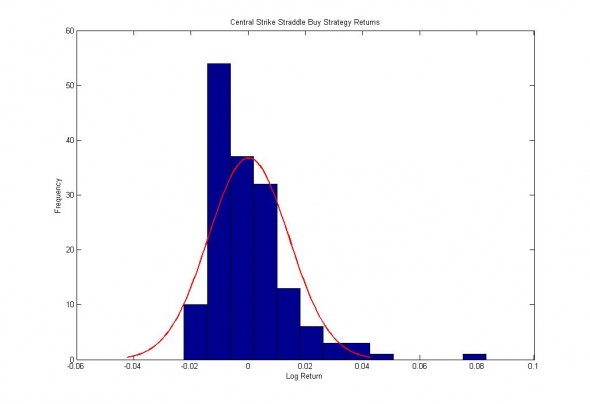
Рис. 9. Распределение прибылей и убытков от покупки стрэддла центрального страйка.
Для всех активов наблюдается схожий финансовый результат, сильно коррелированный по всем страйкам, то есть исключающий возможности misspricing'a по кривизне улыбки и соответствующий только смещённости выборки в пользу роста или падения волатильности.
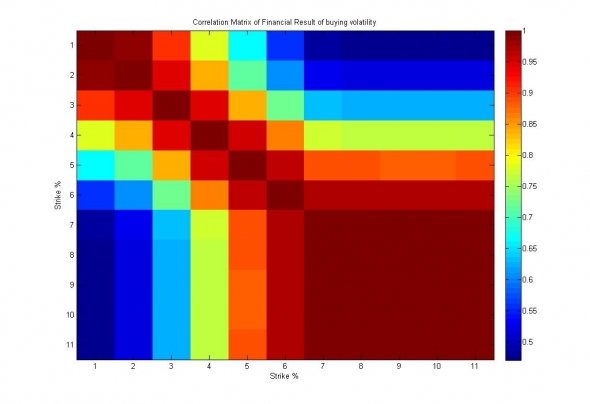
Рис. 10. Изображение корреляционной матрицы финансовых результатов покупки волатильности по разным страйкам
Прим :
Неискушенному читателю может показаться, что вот оно — ГТО! Но это далеко не так. ГТО ГТу — рознь, если дело касается эффективности статистических оценок. Подобрать ГТО «в среднем» — легко, достаточно лишь, чтобы оно совершало локальные взаимозануляющие ошибки. Но такое, «среднее» ГТО, не смотря на свою состоятельность, будет проигрывать любому более эффективному ГТу.
Чтобы назначать цену волатильности, для начала, не плохо было бы принять какую-либо модель волатильности. Например, это может быть модель случайного процесса, подчинённого логистическому распределению:

Рис.1. Распределение логарифмических приращений цен акций ПАО Газпром и их аппроксимация логистическим распределением.
или распределению Лапласа:

Рис. 2. Распределение абсолютных значений логарифмических приращений цен акций ПАО Газпром и их апроксимация экспоненциальным распределением.
Поскольку нам ближе безарбитражные процессы с неравномерным распределением средней мощности (волатильности) во времени (см. «Кому улыбается волатильность»), мы остановимся на втором варианте.
Экспоненциальное распределение это распределение одного параметра — m=sigma - который нам нужно оценить во времени, то есть, принимая во внимание эффект кластеризации волатильности, нам нужно оценить не только форму локального распределения приращений, но и его ширину. Иными словами, помимо самой функции распределения приращений, обладающей некоторой волатильностью (шириной), мы будем ещё учитывать и изменчивость этой волатильности во времени, то есть, непосредственно, волатильность волатильности.
Для этого мы будем пользоваться автоматически настраиваемой EWMA — 40 ( относится к классу ARCH — 40) моделью.
Исходный алгоритм принимает на вход временной ряд из последних 40 логарифмических приращений и последовательно производит действия:
Оценивает параметры EWMA модели
Строит саму модель и оценивает её ошибку
Исходя из полученной модели волатильности и ошибки этой модели на IS выборке оценивает будущую волатильность и распределение ошибок будущей волатильности.
Принципиально, данная автонастраиваемая модель практически не зависит от выбора окна, но, тем не менее, даёт наилучшие результаты на окне равным двум последним месяцам (40).

Рис. 3. Результаты прогнозирования волатильности автонастраиваемой EWMA-40 моделью. Корреляция прогноза и реализации — 77%.

Рис. 4. Гетероскедастичная ошибка прогноза волатильности и его апроксимация распределением Лапласа (экспоненциальным).
Как видно, гетероскедастичная ошибка данной модели повторяет исходное распределение ряда, что говорит о том, что мы определили волатильность правильно, то есть, спрогнозировали непосредственно саму волатильность (ширину распределения), а не что-либо другое.
Теперь, из прогноза волатильности и его гетероскедастичной ошибки, нам осталось только получить распределение логарифмических приращений цен базового актива на ближайшее будущее и можно приступить к расчету цен опционов. Но, такой подход был бы слишком… непрофессионален, поэтому мы зашифруем простые и понятные результаты численного интегрирования экспоненциального распределения в сложную форму улыбки предполагаемой волатильности Блэка-Шоулза, павно перетекающей в дельта-хедж по Корнеру-Фишеру, а чтобы было ещё надёжней — построим не просто улыбку, а рельефную поверхность этой улыбки, протекающей в пространственно-временном континууме, свёрнутом в бублик суперструны.

Рис. 5. Полученная поверхность IV auto-EWMA-40 моделью по Smile Theory Optimal.
Для того, чтобы убедиться в отсутствии misspricing, то есть соответствии STO цен GTO-оптимальным, безорбитражным ценам, проведём симуляцию продажи опционов квалифицированным инвесторам и рассмотрим их результирующую прибыль:

Рис. 6. Симуляция продажи стрэддлов по различным страйкам на БА — TATN. Нормированное уклонение финансового результата от нуля лежит в интервале от -0.8 до -0.16 сигма.

Рис. 7. Симуляция продажи стрэддлов по различным страйкам на БА — SBER. Нормированное уклонение финансового результата от нуля лежит в интервале от 0.4 до 1.4 сигма.

Рис. 8. Симуляция продажи стрэддлов по различным страйкам на БА — MGNT. Нормированное уклонение финансового результата от нуля лежит в интервале от 1.9 до 4.24 сигма. Что, для распределений с «тяжелыми хвостами», соответствующих стратегиям покупки стэдллов — более чем нормально.

Рис. 9. Распределение прибылей и убытков от покупки стрэддла центрального страйка.
Для всех активов наблюдается схожий финансовый результат, сильно коррелированный по всем страйкам, то есть исключающий возможности misspricing'a по кривизне улыбки и соответствующий только смещённости выборки в пользу роста или падения волатильности.

Рис. 10. Изображение корреляционной матрицы финансовых результатов покупки волатильности по разным страйкам
Прим :
Неискушенному читателю может показаться, что вот оно — ГТО! Но это далеко не так. ГТО ГТу — рознь, если дело касается эффективности статистических оценок. Подобрать ГТО «в среднем» — легко, достаточно лишь, чтобы оно совершало локальные взаимозануляющие ошибки. Но такое, «среднее» ГТО, не смотря на свою состоятельность, будет проигрывать любому более эффективному ГТу.
Не является индивидуальной инвестиционной рекомендацией | При копировании ссылка обязательна | Нашли ошибку - выделить и нажать Ctrl+Enter | Жалоба

