31 марта 2023 smart-lab.ru
Часть 1
Невостребованная доходность
Облигации - простое и удобное средство для вложения своих сбережений. Если инвестора не устраивают ставки по банковским вкладам, он ищет аналогичные инструменты на фондовом рынке, и это, конечно, надежные облигации высокорейтинговых эмитентов: ОФЗ, субфедеральные, и другие бумаги, входящие в ломбардный список ЦБ. Инвестор перед покупкой обычно рассматривает такие параметры облигации как дата погашения, величина купона, цена и доходность. И если первые три, как правило, не вызывают вопросов, то последний параметр – доходность – имеет массу интерпретаций, что зачастую приводит к путанице и, как следствие, не всегда корректному сравнению различных облигаций. Всё дело в том, что и цены, и купоны непосредственно наблюдаются на рынке, а доходность – величина расчётная, т.е. выводимая из остальных параметров. Видов доходностей существует много: купонная, текущая, простая, эффективная к погашению, номинальная, к оферте и т.д. и т.п. Какую из них использовать каждый решает для себя, однако в финансовой литературе чаще всего используется так называемая YTM – доходность к погашению. Здесь и далее будем предполагать, что мы живем в мире плоских процентных ставок, т.е. кривые бескупонной доходности – просто константы. Также будем рассматривать только не содержащие опционов облигации с фиксированным купоном.
Для n-летней облигации с ежегодным купоном C и номиналом H YTM приравнивает ее цену P к дисконтированному потоку будущих платежей:
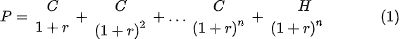
К этой формуле так привыкли, что незаметно для всех она превратилась в формулу «нахождения цены облигации при известной требуемой доходности» Доходность в глазах финансовых менеджеров стала первичным фактором, а цена – производным. Иногда это приводит к недоразумениям. В реальности большинство облигаций на рынке выплачивают купоны не ежегодно, а чаще – раз в полгода, квартал, бывает даже ежемесячно. И сама формула может быть использована для любого числа выплат в год. В большинстве книг по инструментам с фиксированной доходностью ее видоизменяют так, что и выплаты, и доходность рассчитываются на один купонный период:
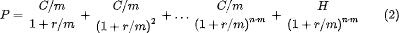
Это общепринятый подход. Именно так, например, считает цену купонной облигации хорошо известная функция Excel ПС(ставка; кпер; плт; [бс]; [тип]). Этот метод хорош тем, что дисконтирует как купоны, так и номинал по одному и тому же правилу, а также позволяет элегантно перейти к непрерывному начислению процентов (устремив m к ∞), используемому в литературе по финансовой инженерии.
Однако, в широко известных онлайн-курсах от Высшей Школы Экономики проф. Н.Берзона (и в учебниках ВШЭ по финансам под его редакцией) можно встретить другую формулу для «вычисления цены купонной облигации с выплатой купонов несколько раз в год»:
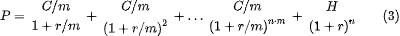
Здесь промежуточные выплаты дисконтируются согласно числу купонных периодов, но сам номинал – на годовой основе. Авторы объясняют это просто – облигация, которая платит купоны чаще одного раза в год, должна стоить дороже, чем аналогичная, но выплачивающая общую сумму купонов целиком, в конце года. И это чистая правда, ведь мы можем реинвестировать купоны и реализовать больший накопленный доход к концу срока погашения. Формула Берзона данному требованию отвечает. Кроме того, мы с удивлением обнаружим, что цена облигации, рассчитанная с помощью формулы (2), если подставить в нее то же значение r, что и в (1), будет не больше, а меньше (!), т.е. облигация с более частыми выплатами купонов парадоксально стоит дешевле. Так в чем тут подвох и почему формула Берзона, несмотря на всю ее привлекательность, все же неточна? Все дело в «доходностях к погашению» используемых в (1) и (2) Они на самом деле различны.
Рассмотрим такой пример:
Цена трёхлетней облигации номиналом 1000 руб. и ежегодным купоном 6% продается по номиналу. Сколько должна стоить такая облигация, если выплата купона будет происходить с периодичностью два раза в год, т.е. исходя из ставки 3% каждые полгода?
Заметим, что первая облигация торгуется с доходностью к погашению, которая равна купонной доходности, т.е. y1=6% при годовом начислении процентов. Для определения требуемой доходности по второй облигации мы должны исходить из принципа отсутствия арбитражных возможностей или Закона Единой цены.Обе облигации должны давать одинаковый фактический накопленный доход при погашении.
Тогда легко показать, что требуемая доходность для купонного периода y0.5 по второй облигации должна удовлетворять соотношению:
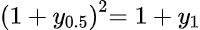
Получим, что y0.5=2.96%, что не равно «ожидаемым» 3%. Именно y0.5 следует подставить вместо r/m в формулу (2) чтобы убедиться, что такая облигация будет стоить дороже номинала, а именно 1002.37 р. Таким образом, для облигации с лучшими характеристиками инвесторы просто потребуют более низкую доходность, r=5.92% (мы должны привести YTM к годовым величинам умножая на 2, чтобы получить требуемую доходность при полугодовом начислении процентов) Между тем, цена такой облигации, найденная по формуле Берзона, будет меньше только что рассчитанной, что создает предпосылки для арбитража и получения неудовлетворительной оценки на экзамене CFA. С другой стороны, разница для низких процентных ставок и коротких горизонтов инвестирования совсем мала, так что формулу Берзона можно смело использовать для приближенных вычислений.
Однако сам по себе способ, используемый в формуле (2) не очень удобен. Для разных облигаций нужно вычислять свои доходности с m-периодным начислением, а это плодит сущности без острой необходимости. Неужели нет универсального подхода к оценке YTM? Он есть, и его можно найти у Дамодарана:

где – ti фракции года, отвечающие времени получения купонов, т.е., например, для облигации с полугодовыми купонами t1 =0.5 , t2 =1 .. tn =n. Всего получается m*n слагаемых.
При этом ставка дисконтирования рассчитывается на годовой основе, единый подход к дисконтированию денежных потоков как для купонов, так и для номинала сохраняется, полученная по формуле (4) цена совпадает с величиной, рассчитанной по формуле (2) при правильной подстановке в (2) доходности к погашению с m-периодным начислением. То есть, если использовать наш пример с 6% купонной облигацией, мы, подставляя в (4) те же 6% получим справедливую цену для облигации с полугодовыми купонами.
Таким образом подходы (2) и (4) в целом эквивалентны и в этом нет ничего необычного, ведь все знакомы с различием между номинальными и эффективными ставками, когда имеют дело с получением банковского кредита. Более того, универсальность формулы (4) еще и в том, что с ее помощью можно дисконтировать и амортизируемые облигации, также она легко модифицируется для расчета цены облигации в межкупонный период.
На сайте «Мосбиржи» https://www.moex.com/ru/bondization/calc для вычисления «эффективной доходности» используется именно формула (4) А вот под «номинальной доходностью» там понимают правильно найденную доходность из формулы (2) Она будет всегда меньше либо равна эффективной.
А какая доходность используется в Quik, когда мы смотрим биржевой стакан? Конечно же, эффективная (4). Можно ли сравнивать облигации, используя эту доходность? Да, с определенными оговорками, можно. В исследуемом нами мире с плоскими и неизменными процентными ставками и невозможностью дефолта эмитента эффективная доходность – единственный критерий для принятия решения о покупке облигации. На рынке, конечно, трудно найти две облигации, отличающиеся только частотой купонных выплат. Но если инвестор их обнаружит, он не должен удивляться тому, что одна стоит дороже другой при одинаковой эффективной доходности в Quik. Причину этого мы и разъяснили выше.
Иногда на форумах бондовиков можно прочесть следующие мнения:
1) Эффективная доходность не учитывает реинвестирование купонов. Это неправда, учитывает. Она ведь устроена таким образом, что предполагает реинвестирование купонов под эту же ставку.
2) Я должен обязательно реинвестировать купон, чтобы получить всю-всю доходность. Здесь тонкость: не реинвестируемый, но потребляемый инвестором купон с точки зрения полезности равен реинвестированному. Я могу проесть его сейчас, а могу реинвестировать и дождаться, когда инфляция его обесценит. Это обычная проблема интертемпорального выбора.
3) Эффективная доходность – это общая доходность, которую я получу, если буду удерживать облигацию до погашения и реинвестировать купоны. Это не так для мира изменяющихся во времени процентных ставок. В момент погашения облигации фактический накопленный доход может быть как выше, так и ниже рассчитанного при помощи YTM. Подробнее этот вопрос будет рассмотрен в последующих статьях.
Часть 2
Дюрация Маколея
“Дюрация — это эффективный срок до погашения облигации”
“С помощью дюрации инвесторы и аналитики измеряют средний срок возврата инвестиций”
“Простыми словами — это количество лет или дней, через которые инвестор вернет вложенные в облигацию деньги”
“Дюрация — это средняя окупаемость инвестиции”
При этом читателю вряд ли будет понятно, что в данном случае означают слова “эффективный” и “средний срок возврата”, а авторы таких статей в детали обычно не вдаются. Мы на примерах покажем, что эти дефиниции иногда могут сбить инвестора с толку, а в некоторых случаях бывают неверны. Мы продолжаем считать, что наши облигации живут в мире плоских процентных ставок, но иногда в нем могут происходить скачкообразные изменения кривой бескупонной доходности.
Дюрация Маколея
В вышеприведенных определениях под дюрацией авторы понимают прежде всего дюрацию Маколея, и она действительно была введена исторически как средневзвешенное время денежных потоков от облигации. (F.Macaulay, 1938) Он, собственно, и рассматривал дюрацию как некую оценку “срока жизни” облигации.
Выражение для дюрации Маколея хорошо известно и мы не будем его приводить, а обсудим лишь некоторые конкретные примеры.
Прежде всего обратим внимание, что единица измерения дюрации — временной интервал (годы, дни и т.д) И наилучшим образом понятию “количество лет или дней, через которые инвестор вернет вложенные в облигацию деньги” отвечает дюрация бескупонной облигации, ведь она в точности равна времени до погашения T (в чем легко убедиться, посмотрев на формулу) Конечно же, деньги вернутся с лихвой, обеспечив держателю процент от вложений, но промежуточных выплат по такой облигации нет, и придется дожидаться погашения номинальной стоимости.
Если облигация платит купоны, то ее дюрация всегда меньше времени до погашения, а чем выше размер купона и/или ставка дисконтирования, тем меньше дюрация. Поэтому возникает восприятие дюрации как “эффективного срока до погашения”, ведь какую-то “часть” инвестор получает заранее, и чем раньше, тем для него лучше. Проблема в том, что данная эффективность в сознании инвестора не имеет четких критериев, она никак и никем количественно не определена. Это скорее качественный показатель, позволяющий судить о том, что одни облигации могут быть лучше других в смысле величины и частоты поступления денежных потоков.
Быть может, формулировка “средний срок окупаемости” подойдет нам больше? В определении срока окупаемости, принятом в корпоративных финансах, временная стоимость денег не учитывается. В этом случае можно показать, что если купонная доходность достаточно велика и близка к ставке дисконтирования, то сумма купонов, полученная за время равное дюрации будет сопоставима с ценой облигации.
Но еще более интересным примером является так называемая “вечная облигация” (или консоль), которая платит только купоны и не имеет номинальной погашаемой стоимости. Выражение дюрации Маколея для консоли, выплачивающей ежегодный купон С, легко вывести, используя стандартные методы анализа: D=(1+r)/r, где r — требуемая доходность при годовом начислении процентов. Цена такой облигации будет равна C/r. Теперь, если перейти к непрерывному начислению процентов (что не так грубо исказит картину, ведь консоли могут выплачивать купоны и ежемесячно), то D=1/y, где у — доходность при непрерывном начислении. И мы получим красивое соотношение: P=D·C, из которого ясно видно, что “вечная облигация” окупается ровно за D лет.
Если рассмотреть другой крайний пример для обычной купонной облигации, — предельно низкие (нулевые) ставки дисконтирования, то в этом случае ее цена равна сумме всех денежных потоков, а значит срок окупаемости должен быть равен времени до погашения. Можно показать, что в этом примере дюрация как правило не превосходит половину срока окупаемости. Не зря в некоторых источниках дюрацию иногда называют «временем полураспада» облигации. Так что, если понимать среднее именно как половину срока окупаемости, то это определение может нам и подойти.
Однако рассмотренный выше подход нас не вполне устраивает, ведь временная стоимость денег для нас имеет значение и полученные купоны мы обязательно реинвестируем. Для того, чтобы получить правильное соотношение для срока окупаемости, с ценой облигации нужно сравнивать не сумму купонов D·C, полученных за время, равное дюрации, а будущую стоимость аннуитета FV[C], рассчитанную для этих купонов. Поэтому, введем так называемый приведенный срок окупаемости PaybackRatio = FV[C]/P, который легко интерпретировать: если он равен или больше единицы, нам удалось отбить вложения в течение t=D, если нет, то увы.
В качестве примера на рис 1. приведены графики приведенных сроков окупаемости 10-летней облигации как функции ставки дисконтирования для различных значений купонной доходности (от 2.5% до 15%).
Видно, что зависимость довольно сложная и дюрация Маколея в нашем случае может выступать в качестве меры «окупаемости» только при достаточно высоких ставках дисконтирования, а в текущих рыночных условиях низких ставок эта мечта вряд ли достижима.
Подводя итог, можно сказать, что дюрация Маколея как «эффективный срок погашения» или «срок окупаемости» безупречно интерпретируется в двух случаях: 1) бескупонная облигация, 2) консоль. Для распространения этого подхода на привычную нам купонную облигацию желательны как высокие ставки дисконтирования, так и большой купонный доход.
И напоследок стоит уточнить, что понятие срока окупаемости, которое обычно применяется к инвестиционным проектам, теряет смысл в условиях торговли высоколиквидными облигациями на ОРЦБ, так как любую купленную облигацию можно продать по усмотрению инвестора в любой удобный момент и тем самым «окупить вложения».
Теперь немного усложним задачу и попросим тиньковскую домохозяйку с помощью известной нам формулы найти дюрацию Маколея, например, для флоатера ОФЗ-24020. И тут ее, скорее всего, постигнет неудача, ведь будущие купоны флоатера неизвестны и зависят от средних значений ставок Ruonia за купонный период, как это определено в спецификации бумаги. Их нельзя подставить в формулу для дюрации. Что делать, как быть?
Нам следует полностью изменить подход к дюрации и отказаться рассматривать ее исключительно с точки зрения средневзвешенного времени получения денежных потоков по облигации. Об этом поговорим в следующей главе.
Просто дюрация
Эффективная дюрация или просто дюрация
Определим дюрацию как меру процентного риска облигации, приблизительно рассчитываемую как относительное изменение ее цены при изменении доходности на 1 п.п.:
Мы отдельно находим цену, когда доходность упала на dy, и когда она выросла на dy. Это не совсем (нормированная на цену) производная, как хочется считать, мы не требуем гладкости цены в окрестности начальной цены. Вообще говоря, таким образом можно определить дюрацию для всех финансовых инструментов, а не только облигаций. И это будет самое общее понятие дюрации, причем для каждого инструмента нам придется предварительно построить свою модель поведения цены в случае малого отклонения доходности вверх или вниз.
Заметим, что для обычной не содержащей опционов облигации с выплатой ежегодных купонов эффективная дюрация D связана с дюрацией Маколея MD соотношением: D = MD/(1+r) В этом случае ее еще называют модифицированной дюрацией. При непрерывном начислении процентов дюрация Маколея и модифицированная дюрация совпадают.
Теперь мы можем найти дюрацию флоатера из следующих соображений. Предположим самый простой случай, когда изменения рыночных ставок приходятся на даты выплаты купонов, а устанавливаемый по флоатеру купон соответствует рыночной требуемой доходности для аналогичных по риску облигаций. Найдем цену флоатера как функцию процентной ставки. Для этого используем метод обратной индукции. Допустим, у нас остался последний купонный период перед погашением. Ставка купона с только что установлена и равна рыночной ставке требуемой доходности r для этого периода. Значит, цена облигации должна равняться ее номиналу H:
Хорошо, отматываем еще один купонный период назад и видим, что ранее установленная ставка купона также равнялась предыдущей рыночной доходности, а будущая цена уже известна, мы ее посчитали, и она равна H. Поэтому и в этот раз облигация должна стоить номинал. Так мы доберемся до самого начала и обнаружим, что вне зависимости от уровня процентных ставок этот флоатер всегда будет стоить номинал. Что это значит? Оказывается, наша облигация не несет в себе процентного риска. А значит ее дюрация D = 0. В реальности, конечно, изменения ставок могут происходить и в межкупонный период, поэтому дюрация примерно равна времени оставшемуся до очередной выплаты купона, но она все равно гораздо меньше срока погашения и поэтому не может быть с ним ассоциирована. Хотя, конечно, можно на это дело взглянуть и так: раз я точно знаю, что в очередную выплату купона цена облигации установится равной ее номиналу, я ее мысленно как бы “погашаю” (могу продать), поэтому и считаю, что купонный период и есть срок до ее погашения.
Неким антиподом флоатера выступает так называемый “обратный флоатер”, устанавливаемая по которому ставка купона имеет обратную зависимость от действующей рыночной ставки. Когда рыночные ставки растут, купонная доходность обратного флоатера падает, и наоборот. В отдельных случаях это полезный финансовый инструмент, так как он предоставляет защиту от падающих процентных ставок, а это как раз наша текущая ситуация. Я очень надеюсь, что Минфин (или кто-то еще) расширит список доступных инвестору ОФЗ, включив в него и обратный флоатер.
Ставку купона обратного флоатера чаще всего устанавливают так: i = k-L·f, где K — некоторая фиксированная ставка, f — плавающая ставка обычного флоатера, а L — так называемый “рычаг” Для того чтобы создать эту необычную облигацию можно использовать следующую схему: как залог берется совершенно обычная купонная облигация с фиксированным купоном K и под нее выпускаются сразу и флоатер, и обратный флоатер. Пропорция между ними будет зависеть от используемого рычага. Денежные потоки от обоих инструментов должны быть в точности равны денежному потоку от облигации-залога. А значит, денежная оценка этой облигации будет равна сумме стоимости флоатера и обратного флоатера в любой момент времени. Соответственно, и дюрация обратного флоатера прямо связана с дюрациями купонной облигации и обычного флоатера.
В качестве примера рассмотрим 10-летнюю купонную облигацию стоимостью 1000 р. и имеющую дюрацию 7 лет. Допустим, мы разделили ее на флоатер и обратный флоатер в отношении 70:30, т.е. наш обратный флоатер будет стоить 300 руб. Из определения дюрации мы знаем, что при изменении рыночных процентных ставок на 1 п.п. цена нашей купонной облигации изменится примерно на 7% или на 70 руб. Точно так же должна будет измениться и совокупная стоимость сконструированного под нее портфеля. О флоатере нам уже известно, что процентный риск у него отсутствует и он не пострадает, поэтому весь удар изменения процентных ставок должен принять на себя его визави; следовательно, цена обратного флоатера изменится на эти же 70 руб, или на 23% Это означает, что его дюрация равна 23 годам, что, согласитесь, куда больше отведенных нашим инструментам 10-ти лет, и тут мы точно не можем опираться на первоначальное понимание дюрации как “эффективного срока до погашения” В реальности все устроено немного сложнее, так как отрицательные ставки по обратному флоатеру обычно не допускаются, и это, в свою очередь накладывает ограничение и на предельный размер верхней ставки по обычному флоатеру.
Теперь рассмотрим пример, взятый из жизни ипотечных облигаций (ИЦБ), ведь волна секьюритизации уже давно докатилась до России. Они обеспечены пулом ипотек и могут рассматриваться как относительно надежные бумаги. В мае 2017 г в банке ПСБ мне предложили принять участие в приобретении выпуска облигаций ипотечного агента ИАВ 5-1-об (ИА Возрождение 5 ООО) Дата погашения 2049 г. Установленная ставка купона 9.25% Казалось бы, из-за такого большого срока это рискованное вложение, но у ипотечных облигаций есть одно замечательное свойство: они амортизируются. Выплаты по ИЦБ осуществляются на периодической основе и состоят из процентного дохода и частичного погашения номинальной стоимости облигаций. При этом, ежемесячная амортизация будет зависеть от количества досрочно выплаченных ипотек за предыдущий месяц. Таким образом, ипотечная облигация имеет встроенный опцион на досрочное погашение ипотечниками и, кроме того, может содержать опцион clean-up, т.е. право эмитента при снижении номинальной стоимости облигации ниже определенного уровня досрочно ее погасить. Из-за наличия этих опционов дюрация ИЦБ не может быть рассчитана простыми методами (по Маколею). Сейчас мы не будем углубляться в методы ценообразования ипотечных облигаций и нахождения их эффективной дюрации, заметим только, что уровень досрочных погашений ипотечниками сильно возрастает с падением ставок в экономике (зачем продолжать платить дорогую ипотеку, когда можно перекредитоваться на гораздо более выгодных условиях?) Вследствие этого растет и величина амортизационных выплат по нашей облигации, что превосходно подтверждается практикой: к настоящему моменту от первоначального номинала ИАВ 5-1-об осталось лишь 10%. За три года она, можно сказать, полностью окупилась.
Раз уж мы заговорили об ипотечных облигациях, следует привести и другой пример. Ипотечную облигацию можно использовать как залог аналогично рассмотренному нами выше примеру с обратным флоатером и разбить ее денежный поток на два составляющих транша: interest only (IO) и principal only (PO)
Если кто-нибудь из читателей разбирался с ипотекой, то он в курсе, что ипотечный кредит это разновидность аннуитета и ежемесячный платеж включает в себя как выплату процентов так и частичную амортизацию кредита. Иногда даже делают такие таблички, где все это расписано на каждый месяц вперед. Я взял отсюда пример такой таблички и красивый рисунок, где хорошо видно как изменяется с течением времени соотношение доли уплачиваемых процентов и погашения части основного долга.
Под пул таких займов и выпускаются ИЦБ.
Упрощенно говоря, в IO покупают столбик “процент к уплате” Если рыночные ставки повышаются, скорость предоплаты имеет тенденцию замедляться и наоборот. Более низкие скорости предоплаты приносят пользу владельцу IO, который хочет, чтобы амортизируемая часть залоговой облигации, на которую начисляется получаемый им процент, оставалась “жирнее” как можно дольше, т.е. он заинтересован в том, чтобы предоплаты осуществлялись как можно медленней. Но как только ипотечные кредиты выплачиваются досрочно, они перестают платить проценты в следующем за произведенной предоплатой месяце. В самом крайне негативном случае инвестор может купитьIO и обнаружить, что весь транш был выплачен в прошлом месяце, о чем будет сообщено только в следующем месяце. Поэтому, IO, как правило, имеют отрицательную дюрацию из-за того, что изменение их цены положительно коррелирует со ставками. И очень трудно объяснить инвестору, что “эффективный срок погашения” его транша равен, например, минус 5 лет.
Кто-то может сказать, а зачем все это нужно, нам за глаза хватает и простых облигаций. Это узкий взгляд на вещи. Наш фондовый рынок ширится и растет, и я выступаю оптимистом в отношении его дальнейшей судьбы. Цены на акции Мосбиржи об этом уверенно сигнализируют. На биржу будут поступать все новые и новые финансовые продукты, чтобы удовлетворить растущие запросы взыскательных инвесторов. Великолепный тому пример — шквал предложения структурных облигаций (например, те же ИОС Сбербанка), наводнивших рынок в последние два года. Поэтому инвесторам нужно хорошо понимать процентные риски, присущие самым разнообразным и причудливым инструментам долгового рынка.
В следующей части мы вернемся к нашей старой знакомой, — дюрации Маколея, которую мы столько раз незаслуженно обижали и постараемся ее реабилитировать. Мы обнаружим у нее одно полезное свойство, которое позволяет до определенной степени не беспокоиться об изменяющихся процентных ставках.
Иммунный ответ
Мы с тиньковской домохозяйкой продолжаем наше совместное путешествие по фантазийному миру облигаций. Предположим, что перед ней встала задача определить накопленную стоимость своей облигации с годовыми купонами на некоторый момент в будущем, который она определяет как свой горизонт инвестирования. Необязательно ждать до времени погашения T, — если бумага длинная, но доходная, можно какое-то время и подержать. Планируемая накопленная стоимость TV (обзовем ее target value) может быть определена из таких соображений: мы должны заглянуть в будущее и рассчитать, какой будет цена облигации Pt через t
Часть 3
Куда кривая вывезет
Ранее мы предполагали, что рыночные ставки плоские, поэтому дисконтировали денежные потоки по облигации с помощью единой ставки — доходности к погашению (YTM). Однако наблюдаемые на рынке доходности государственных облигаций на самом деле зависят от срока до погашения. Графически эта зависимость представляется в виде так называемой кривой доходности или yield curve. Если для построения использовать только что выпущенные облигации, торгующиеся, как правило, возле номинала, получим кривую номинальной доходности (par yield curve) Ее очень удобно интерпретировать, так как в этом случае купонные доходности равны доходностям к погашению. Впрочем, на низколиквидном рынке подобные облигации для всех сроков до погашения удается найти далеко не всегда.
Возникает вопрос, можно ли использовать эти кривые для оценки вновь выпускаемых облигаций? Рассмотрим модельный пример, когда на рынке есть только две облигации с ежегодной выплатой купона торгующиеся по номиналу (100): годовая с купоном 3% и двухлетняя с купоном 6%. Пока мы не будем вдаваться в детали возможных причин различий их доходностей. Если на этом рынке появится еще одна двухлетняя облигация, но уже с купоном 9%, следует ли для расчета ее цены использовать нашу ‘двухлетнюю’ YTM, т.е. ставку 6% ? Тогда бы мы получили цену облигации
P = 9/(1+6%) +109/(1+6%)2 = 105.5. Или, быть может, первый купонный платеж необходимо дисконтировать, используя YTM=3%, и только выплаты второго года по ставке 6% (цена будет равной P = 9/(1+3%) +109/(1+6%) 2 = 105.75)? Оказывается, ни первый, ни второй метод не подходит: можно показать, что в обоих случаях будет возможен арбитраж.
Правильный способ — это считать нашу купонную облигацию портфелем облигаций с нулевым купоном. При этом неявно предполагается, что на рынке могут быть заключены контракты на продажу отдельных купонов, т.е облигацию можно “расщепить” на кусочки. Тогда каждый денежный поток (купоны и номинал) — будет отдельной бескупонной облигацией со своим сроком погашения и ставками дисконтирования r1, r2 для каждого года. Их также называют ставки “спот” (spot rates) Стоимость такого портфеля, а соответственно, и цена новой облигации, будет равна сумме приведенных стоимостей: P = 9/(1+r1) +9/(1+r2 )2 + 100/(1+r2 )2 Поскольку на нашем модельном рынке бескупонных облигаций нет, для вычисления теоретических ставок r1, r2 понадобится определенная процедура, называемая бутстрэппингом. Однолетнюю спотовую ставку r1 легко получить, зная характеристики годовой купонной облигации: 100 = 103/(1+r1), т.е. она попросту равна YTM=3% для годовой облигации. Здесь мы приравниваем 103 к “номиналу” бескупонной годовой облигации, а 100 — к ее цене. Зная r1, двухлетнюю бескупонную доходность r2 теперь можно найти, используя данные (цену и размер купона) по двухлетней купонной облигации из уравнения 100 = 6/(1+3%) +106/(1+r2 )2 Она будет равна r2 = 6.09%, т.е. чуть больше, чем YTM первой “двухлетки” (6%) Теперь легко определить справедливую, т.е. безарбитражную, цену нашей новой двухлетней облигации с 9% купоном: P = 9/(1+3%) +109/(1+6.09%)2 = 105.58. Если рассчитать доходность к погашению новой облигации при данной цене, она окажется равной 5.96%, т.е. будет ниже чем у первой “двухлетки” А это и означает, что мы уже не можем ориентироваться на эфф. доходность (например, в Quik) как на единственный критерий при выборе облигации. Ведь цена получена нами из соображений отсутствия арбитража, т.е старая и новая облигации на модельном рынке должны быть одинаково привлекательными с точки зрения инвестора. Однако доходность к погашению у двух сходных облигаций с тем же сроком до погашения, но разной ставкой купона, оказалась различной. В литературе это принято называть купонным эффектом. В мире плоских процентных ставок купонный эффект отсутствует.
Если бы у нас были облигации с погашением через 3, 4 и т.д. года, соответствующие бескупонные доходности (спотовые ставки) вычислялись бы так же последовательно, одна за одной, в этом и заключается суть бутстрэппинга. Понятно, что для большого массива данных вручную это делать сложно, поэтому на помощь приходит линейная алгебра. Если у нас есть вектор цен облигаций P и соответствующая матрица купонных платежей C, то можно получить вектор дисконтирующих множителей (нормированных цен бескупонных облигаций) d из матричного уравнения d = C-1 P Понятно, что при этом обратная матрица C-1 должна существовать. В Excel для такой операции предусмотрена формула МУМНОЖ(МОБР(...);...) Из вектора d затем легко получить значения спотовых ставок ri, т.к. di = 1/(1+ri)i В приложенных файлах (Excel, Python) я привожу пример использования бутстрэппинга для вычисления спотовой кривой (zero curve) при известных значениях доходностей к погашению (yields)
Еще раз подчеркнем отличие. Кривая доходностей (yield curve) — это кривая ставок YTM имеющихся на рынке купонных государственных облигаций. Спотовая кривая (zero curve) — кривая ставок, по которым следовало бы дисконтировать бескупонные государственные облигации, если бы они присутствовали на этом же рынке. У облигации с ежегодной выплатой купона и погашением через N лет существует единая ставка YTM, которая приравнивает приведенную стоимость денежных потоков по облигации к ее цене. С другой стороны, чтобы получить эту же цену, для дисконтирования соответствующих потоков можно использовать N спотовых ставок. Спотовую кривую также принято называть временной структурой процентных ставок.
Обычно выделяют 4 формы спотовой кривой: нормальную (возрастающую), инверсную (убывающую), плоскую и “сгорбленную”, см. рис:
В зависимости от своей формы спотовая кривая может занимать различное положение относительно кривой доходности. В случае возрастающей кривой доходности, спотовая кривая всегда лежит выше, см. рис 1.
Если кривая доходности убывает, то спотовая кривая лежит ниже. В мире плоских процентных ставок спотовая кривая совпадает с кривой доходности. Следует также отметить, что ставки не могут расти или снижаться вечно. Поэтому, как нормальная, так и инверсная кривые имеют асимптоты: ставки перестают изменяться, начиная с какого-то отдаленного во времени момента.
Для возможности применения метода бутстрэппинга необходима полнота рынка облигаций, т.е для каждого срока до погашения у нас в наличии должны быть какие-нибудь высоколиквидные государственные купонные облигации. Зачастую это не так, поэтому для вычисления бескупонных доходностей используются приближенные (например, метод псевдообратных матриц) или параметрические методы. На сайте Мосбиржи для построения кривой бескупонной доходности (КБД) используется хорошо себя зарекомендовавший параметрический метод Нельсона-Сигеля. На рассчитанной с его помощью КБД указана доходность с ежегодной капитализацией процентов, т.е это уже знакомая нам «эффективная» доходность с сайта Мосбиржи.
Если же мы обратимся к посвященной облигациям страничке смартлаба, то обнаружим там сразу 4 представления некоей “Карты доходности ОФЗ” К сожалению, все они нуждаются в критическом осмыслении. “Кривая купонной доходности” и аналогичная ей “Купонная доходность от срока до погашения” вовсе не кривые, а наборы точек, представляющие собой ставки купонов ОФЗ для различных сроков до погашения. Так как эти ОФЗ выпускались в разные годы, их купонные ставки отражают доходности тех лет, поэтому обнаружить интересную зависимость или как либо систематизировать их нельзя. Но это удобный способ одним взглядом окинуть все ОФЗ в разрезе их купонных доходностей. “Доходность от срока до погашения” это привычная нам кривая доходности (yield curve), а вот “Кривая бескупонной доходности” на самом деле таковой не является, хотя в отдельных случаях может быть к ней близка. Это та же yield curve, но построенная в зависимости от дюрации ОФЗ. Подписи к заголовкам (“полной текущей годовой доходности облигации..”) также неточны — доходность бывает либо полная, либо текущая. Текущая — это отношение купона к цене облигации, а под полной чаще всего понимают простую доходность к погашению, т.е. без сложного начисления процентов, как, впрочем, и отмечено в подписи: “купон + изменение цены к погашению” приведенные к годовым величинам. Однако на самом графике указана не полная или текущая доходность, а доходность к погашению (с ежегодным начислением сложного процента), она же эффективная из Quik или сайта Мосбиржи.
С целью подтверждения некорректности представления КБД в виде зависимости доходности ОФЗ от их дюрации ниже приведен рис 2.
Для купонных облигаций ось абсцисс была деформирована, тогда как для теоретической спотовой кривой она осталась неизменной (дюрация бескупонной облигации равна сроку до ее погашения) Видно, что кривые не совпали, то есть так делать не совсем корректно. В различиях можно убедиться, и сравнив значения КБД с сайта Мосбиржи с доходностями на сайте смартлаба при одной и той же дюрации. На самом деле при некоторых других формах кривой доходности ошибка такого представления может быть очень серьезной. Хотя идею я понимаю — если предположить, что дюрация купонной облигации это в каком-то смысле “эффективный” срок до ее погашения, то можно приблизительно соотнести ее характеристики с бескупонной облигацией той же дюрации. Вместе с тем, несмотря на указанные недостатки, обсуждаемая “Карта доходностей ОФЗ” чрезвычайно наглядна и позволяет, например, сравнивать текущую форму кривой с тем, что было день или месяц назад.
Итак, нам стала понятна важная роль спотовой кривой, или КБД, — она нужна для оценки вновь поступающих на рынок облигаций. В качестве упражнения и руководствуясь формулой 11 из Методики расчета НКД и доходности, аналогичной формуле 4 из части 1, я рассчитал (см. тот же приложенный файл Excel) безарбитражную цену ОФЗ 26235 на дату 01.03.2021. Точность получилась вполне удовлетворительной. Но ведь на рынке есть не только ОФЗ, дающие весьма скромную доходность: многих трейдеров интересуют надежные корпоративные облигации и даже ВДО. Из-за присущего таким бумагам повышенного кредитного риска, их доходности всегда больше, чем у гособлигаций соответствующей дюрации. Эта разница в доходностях обычно выражается в виде кредитного спреда. Некоторое представление о разновидностях кредитных спредов и порядке их расчета можно получить на этом ресурсе. Спреды напрямую зависят от кредитного качества эмитента (вероятности дефолта) и зачастую приводятся аналитиками в обзорах рынка фиксированного дохода.
Предварительно можно сформулировать следующее правило: для вычисления справедливой цены интересующей нас простой купонной облигации необходимо каждый денежный поток (в т.ч. номинал) дисконтировать по спот-ставке, относящейся к периоду его поступления. Ставки спот могут быть получены с помощью КБД путем прибавления к ней Z-спреда, характерного для аналогичных выпусков облигаций, которые уже присутствуют на рынке.
Возникает закономерный вопрос: можем ли мы применять наши выводы о дюрации, сформулированные в предыдущих главах, если форма кривой доходности не является плоской? Оказывается, что в этом случае дюрацию Маколея, аналогично доходности к погашению, уже нельзя считать полностью удовлетворительным параметром. Выражение для дюрации уточняют, чтобы отразить временную структуру процентных ставок и получают дюрацию Фишера-Вейля. Вместо единой ставки YTM каждое слагаемое в ней дисконтируется по спот-ставке соответствующего периода получения денежного потока. При переходе к непрерывному начислению методами вариационного исчисления можно показать, что в случае разового параллельного сдвига кривой доходности инвестор может обеспечить однопериодную иммунизацию портфеля облигаций, если его горизонт ограничен дюрацией Фишера-Вейля. При этом сама кривая может иметь любую форму. В качестве грубого примера “параллельного сдвига” я взял вот этот участок кривой доходности с “Карты ОФЗ” смартлаба:
В уже упоминавшемся файле Excel приведен расчет дюрации Фишера-Вейля для той же модельной кривой доходности. Видно, что полученные значения поначалу слабо отличаются от дюрации Маколея, но это различие увеличивается со сроком до погашения. Инвестору, предпочитающему длинные облигации, необходимо это учитывать.
В следующих частях мы подробнее обсудим временную структуру процентных ставок, их возможную динамику и некоторые стратегии, используемые трейдерами в зависимости от различных форм спотовой кривой.
Очертания будущего
Грядущее под диктовку ФРС
В одном из недавних топиков на смартлабе мое внимание привлек сюжет из финансового шоу про страдающие от бессонницы деньги
Помимо привычных слов о скором обвале фондового рынка ведущий пообещал рассказать и о том, что такое облигации и кривая доходности. Захотелось узнать об этом подробнее. Всё оказалось просто и понятно, эксперт разложил информацию по полочкам:
Когда вы покупаете облигации, вы даете в долг — правительству или компании. Норма дохода по облигации, которую вы желаете получить, обусловлена степенью вашего доверия к заемщику. Банкротной компании нельзя давать деньги под 3% годовых, но под 30% — почему бы и нет, — ведь мы понимаем, что она за год не дефолтнёт (Л — логика). На самом деле всё зависит от кривой доходности, потому что она диктует нам будущее.
На простом жизненном примере ведущий объясняет почему требуемая доходность растет со сроком до погашения:
Можно дать деньги знакомому Васе на три часа, и это будет почти безрисковая операция, а можно на год, но за год может произойти все что угодно, например, Вася сдохнет. Поэтому на длинном горизонте совершенно другие риски. Зачем я буду рисковать? Доживет — не доживет. Пусть деньги отбивают инфляцию, чтобы я не потерял.
Как могут быть связаны возможный уход знакомого Васи из жизни и инфляция, я, признаться, не очень понял, но рассуждения про увеличивающиеся со временем до погашения облигации риски звучат совершенно логично.
Далее ведущий нарисовал кривую доходности в виде части параболы: Это нормальная форма кривой. Чем больше срок до погашения, тем выше премия за риск. Но есть другие разновидности кривой доходности, нарушающие это правило: кривые могут не только расти, но и убывать со сроком до погашения, как если бы одалживающий у вас деньги Вася подобно старому вину со временем только хорошел. И этому тут же нашлось объяснение: в последние годы исказилось всё из-за этих печатных станков. В Европе и Японии всё делается через одно место. Кривая доходности может плавать в зависимости от того, что происходит в экономике страны. Всегда подкупает, когда сложные и непонятные ситуации получают простые и ясные решения. Здесь я полностью солидарен с Валентиной Терешковой: зачем крутить и мудрить, зачем городить какие-то искусственные конструкции?
Как выяснилось, эксперт полностью изучил всё, чем занималась ФРС на протяжении последних ста лет. Он пришел к выводу, что эта организация лажает всегда. От последних заявлений членов ФРС у него идут мурашки по коже. Ведь они буквально всем вешают на уши лапшу и кормят завтраками. Еще ведущий рассказал о спреде 10-2 и инверсии кривой доходности. Наконец, стало понятно, почему весной 2021 нас ожидает крах рынков — автор обнаружил в рыночных данных очень тревожный сигнальный паттерн: один в один повторяется ситуация, предшествовавшая прошлым обвалам. После инверсии спреды развернулись и угрожающе растут. “С Люсей то же самое было перед тем как ее в больницу увезли”
Надо отметить, что сильные эмоции ведущего в отношении лживости и некомпетентности ФРС мне действительно близки. Меня так же как и его раздражает этот утомительный бесконечный рост. Ведь я в нем не участвую, потому что, как и многие другие созерцатели рынка, все время ожидаю обвала, который к всеобщей досаде постоянно откладывается.
Но вернемся к нашим баранам. Ведущий, рассуждая о нормальной форме кривой доходности транслирует основные положения теории предпочтения ликвидности (о чем, возможно, не догадывается, подобно господину Журдену, не знавшему, что он разговаривает прозой) и одновременно ссылается на возможность дефолта умозрительного Васи. Однако вероятность дефолта контрагента может быть важна для маленького банка или страховой компании, а когда мы смотрим на рынок гособлигаций в контексте срока до погашения, всерьез рассуждать о ней, конечно же, нельзя. Примеры с внезапно отбросившим коньки Васей в данном случае неуместны. С другой стороны, в корпоративных облигациях наши вероятности дефолтов уже учтены в спредах к кривой доходности.
Как любой нормальный человек, никогда не работавший в банке и не изучавший теорию вероятности, ведущий шоу путает две вещи:
1) кумулятивную вероятность дефолта (на протяжении какого-то срока), которая нужна для ответа на вопрос: вероятность какого события больше — банкротство случится на протяжении следующих 10 лет или на протяжении следующих 20 лет? Понятно, что так как второе событие включает в себя первое, то в силу неотрицательности и аддитивности вероятностной меры оно имеет более высокую вероятность (точнее не меньшую)
2) интенсивность дефолта, или вероятность того, что дефолт наступит в течение короткого отрезка времени, при условии, что он не произошел в предыдущий период. Эта величина на момент оценки считается постоянной, она инкорпорируется в процентную ставку. При рассмотрении редуцированных моделей зачастую предполагается, что события дефолтов подчиняются пуассоновскому процессу.
Банк постоянно мониторит состояние заемщика, обкладывает его ковенантами и выдает кредиты под надежные залоги, так что ему нечего особо беспокоиться о том, что будет через 10 лет — любые проблемы он замечает сразу и, в случае чего, может требовать досрочного погашения. Зачем ему пытаться оценить вероятность банкротства компании в 8-м или 10-м году, он ориентируется на текущую ситуацию и краткосрочный прогноз. Проценты банк получает ежемесячно. А еще лучше, если это аннуитетные платежи. На рис. 1 видно, каким образом с течением времени аккумулируется ожидаемая прибыль от разницы в процентных ставках между безрисковым займом и относительно надежным корпоративным заемщиком:
Разница в прогнозном валовом доходе растет нелинейно (действует магия сложного процента), компенсируя кумулятивную вероятность дефолта. Для держателей корпоративных и суверенных бондов на рынке деривативов присутствует своя мера оценки риска дефолта (и, одновременно, инструмент защиты) — кредитные дефолтные свопы.
Однако для торгующихся на рынке облигаций действительно важен процентный риск, который тем выше, чем больше срок до погашения. Для дальнего конца кривой он может быть в том числе связан с ожидаемой инфляцией. Но откуда известна будущая инфляция? Точнее, почему имеется уверенность, что инфляция будет только расти, а ведь именно это должно подразумеваться возрастающей кривой доходности при данной предпосылке. Если инфляция постоянна, то такая форма кривой вовсе не обязательна. Почему кривые доходности могут быть иногда плоскими, изогнутыми или даже убывающими функциями срока до погашения? Одних глупых действий ФРС, Европы и Японии, действующими “через одно место” для этого явно не достаточно. Можно задать еще много “почему”, смазывающих четкую картину мира ведущего, однако следует признать, что на самом деле теорий временной структуры процентных ставок несколько, и объяснить все наблюдаемые формы кривой какой-то одной из них не получится.
Немного отвлечемся и сделаем несколько общих замечаний, чтобы освежить в памяти материал прошлых частей. Ставки в американских изданиях чаще всего указываются в виде так называемого bond equivalent yield (BEY) Это номинальные ставки при полугодовом начислении процентов (формула 2 из части 1). Номинальные ставки удобны тем, что когда они применяются к конкретному периоду, их просто делят на число периодов начисления процентов (нет компаундинга) Если, например, задана спотовая кривая вида r0.5= 4%, r1=4.5%, цена полугодовой облигации находится как 1000/(1+4%/2)=980.39, а годовой как 1000/(1+4.5%/2)2 =956.47
В российской традиции на кривой бескупонной доходности указана эффективная доходность с годовым начислением процентов (формула 4 из части 1). Если использовать те же значения из примера r0.5= 4%, r1=4.5%, цена облигации с погашением через полгода будет равна 1000/(1+4%)0.5 = 980.58, а цена годовой: 1000/(1+4.5%) =956.94.
На самом деле, как мы хорошо помним, первичны всегда цены облигаций, а уж какую доходность мы из них извлечем — номинальную, эффективную, текущую, с каким видом начисления процентов и т.д. — это уже наше дело. Именно потому, когда говорят, что инвесторы требуют такую-то доходность, не конкретизируя, что именно имеют ввиду, это зачастую приводит к недопониманию и ошибкам в расчетах. Доходности важны и удобны для теоретических изысканий, они просты в применении, и у них нет сроков погашения, но все безарбитражные доводы строятся только на ценах облигаций и их денежных потоках. Практики зачастую работают не с доходностями напрямую, а с дисконт-факторами (текущая стоимость 1 ден. единицы, получаемой в будущем) и строят дисконтные кривые вместо кривых доходностей. В наших примерах мы зачастую будем использовать непрерывное начисление процентов как одно из самых удобных. Мы можем легко переходить от непрерывного начисления процентов к ежегодному с помощью преобразования exp(y∙T)=(1+ r)T
Понятие о форвардных ставках.
В дальнейшем нам понадобится представление о подразумеваемых форвардных ставках. Они естественным образом возникают в следующей гипотетической ситуации. Предположим, клиент приходит в банк и говорит: “Я хочу взять кредит на год, но не сейчас, а через год. Какую ставку вы мне можете гарантировать на этот момент, если мы сейчас подпишем обязывающие документы?” Возможно, клиент опасается неблагоприятного развития ситуации на рынке заимствований — взрывного роста инфляции и краткосрочного повышения ставок. С целью упростить пример допустим, что банк приравнивает кредитный рейтинг клиента к рейтингу государственных обязательств страны. Пусть банк наблюдает текущую кривую доходности: {r1=4%, r2 =5% => P(0,1) =100/(1+r1)= 96.15, P(0,2) =100/(1+r2)2 = 90.70} Тогда он может легко зафиксировать годовую форвардную ставку 1f1 (т.е., ставку, действующую с первого года на второй) путем следующих операций. Банк продаст в короткую одну двухлетнюю бескупонную облигацию за 90.70 и на вырученные деньги купит P(0,2)/P(0,1) = 0.943 частей однолетней (опять же ради простоты допустим, что облигации можно приобретать “дробными” частями). Начальные затраты у банка будут нулевые, т.к. 0.943·96.15=90.70. Через год короткая облигация будет погашена, что принесет банку 90.70·(1+r1) = 94.33 наличных и эти деньги он может выдать клиенту на год в кредит.
Поскольку еще через год сам банк должен будет вернуть номинал (100) от проданной ранее двухлетней облигации, то изначально он должен назначить клиенту такую годовую форвардную ставку 1f1 , чтобы выполнялось условие отсутствия арбитража: 100= 94.33·(1+1f1 ), откуда легко вычислить 1f1 = 6%
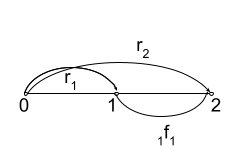
Если вернуться к ценам облигаций, можно записать выражение для 1f1:
1 + 1f1 = P(0,1)/P(0,2). Это же условие можно записать, используя только ставки: (1+r2)2 = (1+1f1)(1+r1) Отсюда наглядно видно, что 1f1 является “ставкой безубыточности”, обеспечивающей равенство стратегий: 1) купить двухлетнюю облигацию, или 2) купить короткую облигацию, а через год реинвестировать еще на год.
Похожие рассуждения можно провести для любого периода в будущем и вывести простое соотношение для спотовых и форвардных ставок (в данном случае запись mfn означает, что ставка применяется для года m и действует n лет)
(1+rn+m)n+m = (1+mfn)n(1+rm)m
В самом общем случае форвардная ставка – это такая устанавливаемая сегодня процентная ставка, которая будет выплачена за пользование деньгами, занятыми на некоторый определенный срок в определенный момент в будущем.
Существует несколько форм записи для форвардной ставки. Иногда пишут fmn или f(m,n) и подразумевают, что ставка действует с года m по год n (а не n лет). Для годовых форвардных ставок могут использовать обозначение fm — это краткосрочная форвардная ставка, действующая с года m до года m+1. При непрерывном начислении процентов используют так называемую мгновенную форвардную ставку f(0, t). Она получается из обычной форвардной ставки F(0,t,T) - (ставки назначаемой в момент времени 0, начинающей действовать в момент t, до момента T) путем предельного перехода t→T. Мгновенная форвардная ставка начисляется на бесконечно малый отрезок времени в будущем.
Однолетние форвардные ставки образуют так называемую кривую краткосрочных форвардных ставок. Она приведена на рис 2 для примера из прошлой части.
Можно показать, что эти форвардные ставки fi ( i < n, f0 = r1 ) связаны со спотовой ставкой rn соотношением,
(1+f0)(1+f1)(1+f2)..(1+fn-1) = (1+rn)n
т.е. спотовая ставка — это среднее геометрическое соответствующих ей годовых форвардных ставок. Поэтому, при положительном наклоне спотовой кривой наша форвардная кривая всегда лежит выше, а ее форма определяется крутизной наклона спотовой кривой. При выходе кривой бескупонной доходности на плато такая форвардная кривая к ней фактически примыкает. Поскольку между спотовыми и форвардными ставками устанавливается взаимно однозначное соответствие, последние наравне со спотовыми могут использоваться для дисконтирования денежных потоков по облигации. Помимо этого форвардные ставки нужны для оценки контрактов FRA и процентных свопов.
Поскольку спотовая кривая порождает целое семейство форвардных кривых (не только для краткосрочных ставок), с их помощью можно построить “ожидаемую” (т.е. подразумеваемую текущей временной структурой) динамику спотовых кривых во времени. Например, подразумеваемая спотовая кривая через год — это форвардные ставки с 1-го года на второй, с 1-го на третий, и т.д. Мы как бы движемся вперед во времени и наблюдаем всё уменьшающийся кусочек видоизменяющейся спотовой кривой “из будущего”. 10 летний форвард на рис. 3 — ожидаемый через 10 лет вид спотовой кривой для следующих 11 лет. А 15-летнему форварду соответствует подразумеваемая через 15 лет спотовая кривая, состоящая всего из 6 точек. Таким образом, предполагается, что инвестор через 15 лет будет наблюдать убывающую кривую бескупонной доходности (по крайней мере на протяжении первых шести лет)
Поэтому зачастую пишут, что форвардные ставки отражают мнение рынка о будущих процентных ставках (более подробно это будет рассмотрено при обсуждении теории ожиданий) Однако для непрофессионального участника рынка практическая польза от них следующая: они помогают принять решение, например, в выборе между стратегиями 1) покупка и удержание двухлетней облигации и 2) последовательная “перекладка” из одной короткой облигации в другую. Если инвестор уверен, что в следующем году краткосрочные ставки вырастут сильнее, чем подразумеваемая форвардная ставка, для него имеет смысл находиться в коротких облигациях (при горизонте инвестирования два года)
В следующей части этой же главы мы непосредственно перейдём к обсуждению гипотез, объясняющих временную структуру и поймём, почему кривые доходности не выглядят так, как их нам рисует Василий Олейник.
Гипотезы, объясняющие временную структуру
Как мы заметили в ч. 2., несмотря на разнообразие форм, в литературе выделяют определенную типологию и динамику кривых доходности.
Также существует несколько устойчивых наблюдений, которые должна объяснять любая содержательная теория срочной структуры процентных ставок.
Как краткосрочные, так и долгосрочные ставки движутся преимущественно вместе, т.е. между ними существует положительная корреляция.
Если краткосрочные ставки находятся на исторически низких уровнях, кривая в большинстве случаев будет иметь нормальную форму. Если же краткосрочные ставки достаточно высоки по сравнению со своими историческими значениями, кривая, скорее всего, станет инвертированной.
Краткосрочные ставки более волатильны, чем ставки по длинным облигациям.
Кривая обычно имеет положительный наклон.
ГИПОТЕЗА ОЖИДАНИЙ
Одной из первых и наиболее представительной теорий временной структуры является гипотеза ожиданий. Она подразделяется на несколько ветвей. Две основные: гипотеза чистых ожиданий (pure (or unbiased) expectation hypothesis) и гипотеза локальных ожиданий (local expectation hypothesis); две вспомогательные: return to maturity expectation hypothesis, yield to maturity expectation hypothesis
Ключевое предположение гипотезы чистых ожиданий состоит в том, что облигации с различными сроками до погашения являются совершенными заменителями (субститутами) Инвестору должно быть все равно как поступить: купить длинную облигацию, или перекладываться из одной короткой в другую. На любом определенном им горизонте инвестирования обе стратегии должны приносить одинаковый доход. Инвестор может купить пятилетнюю облигацию, или сначала двухлетнюю, а потом трехлетнюю, или каждый раз покупать годовые, — разницы в полученном через пять лет доходе, с точки зрения теории чистых ожиданий, — не должно быть никакой. Для того чтобы этот подход работал, необходимо, чтобы долгосрочные процентные ставки были равны среднему (среднему геометрическому) от ожидаемых краткосрочных ставок. Эти ожидаемые краткосрочные ставки должны совпадать с подразумеваемыми форвардными ставками, т.е. годовая форвардная ставка будет являться несмещенной оценкой будущей краткосрочной ставки. Иными словами, вся временная структура будет определяться исключительно ожиданиями инвесторов. Долгосрочные процентные ставки отражают ожидания краткосрочных ставок.
Форвардная ставка с 4-го года на 5-й равна 8%? Значит именно такую годовую спотовую ставку в среднем ожидают инвесторы спустя 4 года.
Если кривая доходности имеет положительный наклон, то инвесторы полагают, что в будущем начнется рост краткосрочных спотовых ставок. А значит, долгосрочная ставка как среднее геометрическое ожидаемых краткосрочных ставок (и их несмещенных оценок — форвардных ставок) должна быть выше, чем текущая краткосрочная ставка. Если это будет не так, уверенные в будущем росте ставок инвесторы станут приобретать только краткосрочные облигации, чтобы затем роллировать свою позицию.
Как же ожидания повышения ставок повлияют на поведение участников и, таким образом, вызовут изменение в наклоне кривой? Возможны следующие механизмы:
Инвесторы с небольшим горизонтом инвестирования будут покупать короткие облигации, а “долгосрочники” перестанут приобретать длинные из-за опасения роста ставок. Вместо этого они тоже купят короткие в ожидании подходящего момента для нового вложения средств.
Спекулянты начнут шортить длинный участок кривой.
Предложение длинных облигаций увеличится, так как все эмитенты будут стараться выпустить длинные облигации под низкую ставку. В качестве примера можно привести крупные российские банки, приступившие к выпуску “вечных” облигаций на дне цикла снижения ключевой ставки ЦБ.
Гипотеза локальных ожиданий не утверждает, что любая стратегия “ купил, держи или перекладывайся” даст одинаковый доход на любом заданном горизонте инвестирования. Предполагается, что это выполняется только для короткого срока инвестиций (полгода, год) То есть, например, двухлетняя и 10-летняя облигации полностью взаимозаменяемы, но при удержании их не более полугода. Положительная разница в доходностях длинных и коротких облигаций объясняется следующими соображениями
обе облигации на горизонте полугода принесут один и тот же доход
после этого инвесторы в среднем ожидают роста процентных ставок
С теоретической точки зрения гипотеза локальных ожиданий более предпочтительна, так как в ней отсутствует возможность для арбитража. Практика, однако, показывает, что даже эта гипотеза плохо работает — чаще всего непродолжительное инвестирование в долгосрочные облигации дает больший прирост капитала, чем приобретение коротких на тот же срок.
Return to maturity expectation hypothesis или гипотеза прироста капитала к погашению предполагает, что полный доход от инвестиций в серию последовательно приобретаемых краткосрочных облигаций будет совпадать с прибылью от удержания одной бескупонной облигации до ее погашения на определенном инвестором горизонте. Yield to maturity expectation hypothesis (гипотеза ожиданий доходности к погашению) схожа по построению с гипотезой прироста капитала, однако здесь используется не полный доход в конце срока, а (периодическая) аннуализированная доходность в двух сравниваемых стратегиях.
Математическое описание гипотезы ожиданий проще всего провести на примере бескупонных облигаций, используя непрерывное начисление процентов и логарифмические цены. Здесь и далее мы предполагаем, что ставки облигаций с различными сроками до погашения это случайные величины, каким-то образом коррелированные между собой.
Пусть Pₜ — обычная цена дисконтной облигации в момент времени t, а pₜ = ln(Pₜ) — логарифмическая. Предположим, что обычные цены Pₜ нормированы, т.е. номинал облигации равен 1. Тогда pₜ < 0. Обозначим как pₜ⁽ⁿ⁾ логарифмическую цену облигации с погашением через n периодов.
Теперь мы можем ввести доходность к погашению
yₜ⁽ⁿ⁾ = [-1/n]·pₜ⁽ⁿ⁾
однолетние форвардные ставки
fₜ⁽ⁿ⁾ = pₜ⁽ⁿ⁺¹⁾ — pₜ⁽ⁿ⁾
ставку за период владения (доходность от продажи облигации, купленной ранее):
rₜ₊₁⁽ⁿ⁾ = pₜ₊₁⁽ⁿ⁻¹⁾ — pₜ⁽ⁿ⁾
(Обозначение pₜ₊₁⁽ⁿ⁻¹⁾ указывает на факт, что продаваемая через год облигация автоматически имеет более раннее погашение)
премию за срок владения облигацией (избыточную доходность)
rxₜ₊₁⁽ⁿ⁾ = rₜ₊₁⁽ⁿ⁾ - yₜ⁽¹⁾
Положения гипотезы ожиданий состоят из нескольких в целом эквивалентных утверждений
А. Если мы покупаем длинную n-летнюю облигацию или роллируем вперед однолетнюю n раз, то в среднем для доходностей к погашению выполняется соотношение ( Eₜ [ ]— условное математическое ожидание в момент времени t)
yₜ⁽ⁿ⁾ = Eₜ[yₜ⁽¹⁾ + yₜ₊₁⁽¹⁾ +… + yₜ₊₁⁽¹⁾ yₜ₊ₙ₋₁⁽¹⁾]/n
Б. Инвестор с небольшим горизонтом также может купить либо короткую облигацию, либо длинную и продать ее через год. Тогда должно быть выполнено условие безарбитражности
yₜ⁽¹⁾ = Eₜ[rₜ₊₁⁽ⁿ⁾], т.е. Eₜ[rxₜ₊₁⁽ⁿ⁾] =0
В. Форвардная ставка равна ожидаемой краткосрочной ставке через n-1 лет:
fₜ⁽ⁿ⁾ = Eₜ[yₜ₊ₙ₋₁⁽¹⁾]
Теперь мы можем ввести доходность к погашению
yₜ⁽ⁿ⁾ = [-1/n]·pₜ⁽ⁿ⁾
однолетние форвардные ставки
fₜ⁽ⁿ⁾ = pₜ⁽ⁿ⁺¹⁾ — pₜ⁽ⁿ⁾
ставку за период владения (доходность от продажи облигации, купленной ранее):
rₜ₊₁⁽ⁿ⁾ = pₜ₊₁⁽ⁿ⁻¹⁾ — pₜ⁽ⁿ⁾
(Обозначение pₜ₊₁⁽ⁿ⁻¹⁾ указывает на факт, что продаваемая через год облигация автоматически имеет более раннее погашение)
премию за срок владения облигацией (избыточную доходность)
rxₜ₊₁⁽ⁿ⁾ = rₜ₊₁⁽ⁿ⁾ - yₜ⁽¹⁾
Положения гипотезы ожиданий состоят из нескольких в целом эквивалентных утверждений
А. Если мы покупаем длинную n-летнюю облигацию или роллируем вперед однолетнюю n раз, то в среднем для доходностей к погашению выполняется соотношение ( Eₜ [ ]— условное математическое ожидание в момент времени t)
yₜ⁽ⁿ⁾ = Eₜ[yₜ⁽¹⁾ + yₜ₊₁⁽¹⁾ +… + yₜ₊₁⁽¹⁾ yₜ₊ₙ₋₁⁽¹⁾]/n
Б. Инвестор с небольшим горизонтом также может купить либо короткую облигацию, либо длинную и продать ее через год. Тогда должно быть выполнено условие безарбитражности
yₜ⁽¹⁾ = Eₜ[rₜ₊₁⁽ⁿ⁾], т.е. Eₜ[rxₜ₊₁⁽ⁿ⁾] =0
В. Форвардная ставка равна ожидаемой краткосрочной ставке через n-1 лет:
fₜ⁽ⁿ⁾ = Eₜ[yₜ₊ₙ₋₁⁽¹⁾]
Гипотеза ожиданий хорошо объясняет первые три из четырех наблюдений, сформулированных в самом начале главы.
Например то, почему доходности облигаций с различными сроками до погашения движутся однонаправленно. Допустим, ЦБ начал цикл повышения ключевой ставки. Тогда участники рынка могут ожидать, что сегодняшний рост краткосрочных процентных ставок продолжится некоторое время в будущем. И это ожидаемое повышение однолетних ставок вызывает рост долгосрочных ставок уже в текущем периоде (это прямо следует из формулы утверждения А)
Во-вторых, она дает ответ на вопрос, почему кривая доходности имеет положительный наклон, когда краткосрочные ставки низки, и отрицательный наклон, когда краткосрочные ставки высоки. Когда краткосрочные ставки находятся ниже долгосрочной средней, то участники рынка ожидают их повышения в будущем, а когда находятся выше долгосрочной средней, то их ожидания состоят в том, что в будущем они снизятся. Соответственно долгосрочные ставки, как средние от ожидаемых краткосрочных ставок будут выше или ниже средних краткосрочных ставок.
И кроме того, данная гипотеза объясняет более высокую волатильность краткосрочных ставок по сравнению с долгосрочными Поскольку процентные ставки имеют свойство возвращаться к среднему, то среднее краткосрочных ставок должно иметь меньшую волатильность, чем сами эти ставки по отдельности (волатильность средней, как известно уменьшается с увеличением количества слагаемых)
Вместе с тем, гипотеза ожиданий в чистом виде не так хорошо согласуется с известными данными. Во-первых, на практике чаще всего наблюдается так называемая нормальная (т.е. возрастающая) форма кривой доходности. В этом случае, согласно гипотезе, краткосрочные процентные ставки должны чаще находиться ниже долгосрочного среднего уровня, чего на практике не наблюдается. Во-вторых, форвардные ставки, являющиеся в теории чистых ожиданий несмещенными оценками будущих краткосрочных ставок, вовсе не выступают предикторами будущих краткосрочных ставок. Иначе будущие цены облигаций можно было бы заранее рассчитать, а будущий доход от инвестиций был бы известен заранее и не зависел от структуры портфеля. На самом же деле, как установлено в многочисленных исследованиях, нет строгой корреляции между будущими краткосрочными ставками и подразумеваемыми форвардными ставками. Наихудшие прогнозы теория ожиданий дает на горизонте ближайших нескольких лет.
ГИПОТЕЗА ПРЕДПОЧТЕНИЙ ЛИКВИДНОСТИ
Для объяснения устойчивости положительного наклона кривой доходности гипотезу ожиданий дополняют гипотезой предпочтений ликвидности (иногда она сразу рассматривается как составная часть гипотезы ожиданий) В данной интерпретации к “условному среднему” ожидаемых краткосрочных ставок добавляется еще и риск-премия, которая также зависит от срока до погашения:
yₜ⁽ⁿ⁾ = Eₜ[yₜ⁽¹⁾ + yₜ₊₁⁽¹⁾ +… + yₜ₊₁⁽¹⁾ yₜ₊ₙ₋₁⁽¹⁾]/n +RiskPremium⁽ⁿ⁾
В этом случае облигации считаются несовершенными заменителями.
Теория предпочтений ликвидности хорошо объясняет преимущественно нормальную форму кривой, ведь премия за риск строго положительна. Также ее выводы согласуются с однонаправленностью движения ставок для облигаций с различными сроками до погашения — если долгосрочные ставки вырастут, часть инвесторов устроит эта повышенная доходность и, чтобы зайти в длинные, они начнут продавать короткие облигации, вызывая рост доходности последних. Таким образом возникает корреляция в ставках у облигаций с различными сроками до погашения.
Однако, теперь, если кривая доходности имеет положительный наклон, это не обязательно означает, что инвесторы ожидают роста краткосрочных ставок в будущем. В этом случае форма кривой может полностью определяться риск-премией. Или, например, ожидаемое падение ставок может быть в точности компенсировано премией за ликвидность — и в результате мы получим плоскую форму временной структуры. А если спотовая кривая имеет инверсный вид, то инвесторы ожидают в будущем падение ставок, причем довольно серьезное, чтобы оно обнулило влияние положительной премии за риск “утраты ликвидности”
Сходства и различия двух гипотез в трактовке прогноза динамики процентных ставок суммированы в таблице ниже.
Нужно понимать, что в современном представлении “временная утрата ликвидности” не означает, что погашения приходится слишком долго ждать. Рынок облигаций может быть достаточно ликвиден, чтобы без особых хлопот продать необходимый объем. В данном случае проблема с ликвидностью — это чисто ценовой риск. При неблагоприятном сценарии неожиданного повышения ставок инвестор может быть “заперт” в своих долгосрочных облигациях, не желая продавать их с убытком, хотя ему могут понадобиться средства. Утрата ликвидности временная, инвестор может дождаться лучших времен, ставки развернутся, и облигации снова “отрастут” Яркий тому пример — 2020 год, когда пришла весна на рынок ОФЗ. Или же наша текущая ситуация, в которой ЦБ ускоренными темпами поднимает ключевую ставку, пытаясь обуздать инфляционные ожидания. С короткими облигациям такой проблемы не возникает.
В качестве иллюстрации рассмотрим две стратегии: покупка двухлетней облигации или последовательное приобретение двух однолетних. Купонная доходность в обоих случаях равна 5% годовых. Если ставки на протяжении двух лет останутся неизменными, обе стратегии приносят одинаковый доход (красная линия на рисунке)
У стратегии роллирования короткой облигации выше риск реинвестирования, — при изменении уровня процентных ставок можно как выиграть, так и потерять по сравнению с удержанием до погашения длинной облигации. У двухлетней инвестиции выше риск изменения цены (capital gain risk) Этого риска инвесторы опасаются куда больше. Подарок судьбы в виде прироста капитала при упавшей процентной ставке они ценят меньше, чем временную просадку при внезапном повышении ставок. Такая асимметрия носит название неприятие риска (risk aversion)
Для покупателей с коротким горизонтом инвестирования принципиально важна определенность в полученном спустя год доходе. Они не хотят гадать, куда могут пойти ставки и отказываются от гипотетической возможности заработать на их падении. Они сосредотачивают свой интерес в краткосрочных облигациях, значительно увеличивая спрос на коротком конце кривой доходности. Поведение заемщиков варьируется относительно их горизонта. Заемщики с коротким горизонтом заимствуют на краткосрочных рынках, им нет смысла выпускать обязательства на более длинный срок. Долгосрочные заемщики, наоборот, предпочитают длинные займы, чтобы не сталкиваться с необходимостью ежегодного рефинансирования. Обычно заемщики нацелены на долгосрочные займы и согласны платить премию. Поэтому, как правило, и инвесторы, и заемщики согласны с необходимостью уплаты временной премии.
ТЕОРИИ СЕГМЕТАЦИИ РЫНКА И ПРЕДПОЧИТАЕМОЙ СРЕДЫ ОБИТАНИЯ
Приверженцы теории сегментации рынка (market segmentation theory) считают, что облигации с различными сроками до погашения не являются заменителями друг для друга. Одни участники рынка предпочитают работать на коротком участке кривой доходности, в то время как другие на дальнем, таким образом активность экономических агентов может быть сосредоточена в отдельных областях рынка, между которыми нет никакой взаимосвязи. Например, банкам для ежедневного ALM-менеджмента, а также в силу регуляторных требований необходимы краткосрочные инструменты, тогда как крупные пенсионные фонды предпочитают приобретать облигации с большим сроком до погашения. Поэтому возникает несколько сегментов рынка облигаций, и равновесие в каждом из них обеспечивают свои отдельные кривые “спроса-предложения” Предполагается, что между этими сегментами невозможен арбитраж. Надо отметить, что теоретически подобное поведение участников может приводить к разрывам в кривой доходности, т.е. она будет распадаться на несколько кусков, чего на практике обычно не наблюдается. Кривые выглядят достаточно гладкими, хотя это, конечно, может быть следствием магии интерполяции. Теория сегментации хорошо объясняет возрастающую форму кривой: на коротком конце сосредоточены в основном инвесторы, предпочитающие краткосрочные инвестиции, соответственно в этом участке возникает избыток денежного предложения. На длинном участке кривой, наоборот, инвесторов не так много, там преобладают заемщики.
Теория предпочитаемой среды (preferred habitat theory ) может рассматриваться как разновидность теории ожиданий/теории предпочтений ликвидности с одним уточнением: премия за риск не обязательно прямо связана со сроком до погашения. Инвесторы, как правило непрофессиональные, предпочитают облигации какой-то конкретной дюрации: кто-то из них облюбовал короткие, кому-то больше по душе средние или длинные. В основном, покупатели предпочитают короткий участок кривой, а продавцы — длинный. Однако как те, так и другие, могут быстро переключиться на любой другой участок кривой, если им понравятся тамошние низкие цены (высокая доходность) В каждой из таких «сред» существуют свои спрос и предложение, что может приводить к любому знаку и изменению премии за срок. Миграцией по кривой доходности можно объяснить практически любую форму кривой.
ВЛИЯНИЕ ВЫПУКЛОСТИ НА ФОРМУ КРИВОЙ ДОХОДНОСТИ
В предыдущих главах мы выяснили, что такое дюрация и определили ее как меру процентного риска по облигации. Но можно пойти дальше и рассмотреть чувствительность к процентным ставкам уже для самой дюрации. Эта чувствительность носит название выпуклости. Фактически, выпуклость это поправка второго порядка, коэффициент в следующем элементе разложения функции в ряд Тейлора. Так как зависимость текущей стоимости облигации от уровня ставок является нелинейной, дюрация, как линейная мера риска, может весьма неточно отражать процентное изменение цены, особенно если доходность отклонится на значительную величину. Выпуклость уточняет влияние доходности на цену облигации.
Она также позволяет учесть асимметричность влияния ставок при их увеличении или уменьшении. Цена облигации более чувствительна к падению процентных ставок, чем к их росту. Допустим, например, что при увеличении доходности на 1 п. п. цена некоторой облигации упадет на 9%, а если ставки снизятся на ту же величину (1 п. п.), ее стоимость может вырасти на 11%, т.е. это больше в абсолютном выражении. Формула для выпуклости в случае простой не содержащей опционов облигации хорошо известна. Мы также можем уточнить выражение для процентного риска облигации:
dP/P = — Ddy +½ C (dy)²
Так как C > 0, то вне зависимости от направления движения процентных ставок, второе слагаемое всегда дает положительную прибавку. Поэтому, кажется вполне очевидным, что чем больше выпуклость, тем лучше.
Ниже приведен иллюстрирующий положительные свойства выпуклости рисунок, на который любят ссылаться различные популярные сайты о финансах.
Сам по себе рисунок, конечно, неточный, так как
1. Цена облигации при нулевых ставках не уходит на бесконечность, функцию P(y) не надо путать с гиперболой.
2. Зависимость P(y) монотонная и убывающая, и цена простой купонной облигации не будет, начиная с какого-то момента, расти одновременно с ростом ставки, как это происходит в правой части кривой “Bond A”.
3. Ситуация, когда у двух простых купонных облигаций могут быть одновременно равны цены, дюрации и доходности к погашению (точка (P*, Y*) на рисунке) на практике встречается крайне редко. Она, например, достижима для длинных бумаг, если рыночные ставки достаточно высоки, — т.е. касание кривых должно происходить в дальней правой части рисунка. Подобную комбинацию легче осуществить для портфелей облигаций.
Часто публикуемые на трейдерских форумах бесплатные советы “при прочих равных” выбирать бумаги с меньшей дюрацией или большей выпуклостью несут в себе мало пользы именно из-за отсутствия главного условия — неизменности всех остальных параметров. В подавляющем большинстве случаев все приятные плюшки уже в ценах. Если бумага чаще выплачивает купоны, т.е. имеет меньшую дюрацию, она будет торговаться дороже аналога (в смысле риска, срока до погашения и т. д.) с той же купонной доходностью, но меньшей частотой купонных выплат. Схожая картина и с выпуклостью. Не стоит надеяться на ситуацию, что вы обнаружите бумаги одной и той же дюрации, с одинаковой ценой и доходностью, но различными выпуклостями — такие облигации практически невозможно найти на рынке. Поиск подходящего портфеля-заменителя с лучшими характеристиками также затруднителен по причинам, которые мы обсудим ниже. Кроме того, эффект выпуклости на порядок слабее, т.е. не следует переоценивать его влияние на изменение цен облигаций, особенно для бумаг с небольшой дюрацией.
У выпуклых функций есть еще одно любопытное свойство, хорошо известное в теории вероятностей. Оно связано с неравенством Йенсена. Применительно к будущей краткосрочной ставке r (как мы помним, это случайная величина) необходимо выполнение следующего условия (E[..] означает математическое ожидание):
E[1/(1+r)] > 1/E[1+r] = 1/(1+E[r])
Рассмотрим эффект выпуклости на примере бескупонной облигации с погашением через два года и номиналом 100.
Допустим, текущая доходность по двухлетним бумагам составляет 8% и участники рынка не ожидают изменения ставок через год. Тогда цена такой облигации будет равна 100/1.08² = 85.73. Теперь предположим, что ставка через год может равновероятно снизиться или вырасти на 3 п. п. Ожидаемая ставка, будет равна текущему значению:
E[r] = 0.5∙5%+0.5∙11% = 8%.
Но для ожидаемой цены всё обстоит иначе:
E[P] = 100∙(1/1.08)∙(0.5/1.05+ 0.5/1.11) = 85.80, что незначительно больше, чем 100/1.08² = 85.73.
Теперь, если посчитать новую требуемую доходность (двухлетнюю спотовую ставку) исходя из ожидаемой цены, она окажется меньше, чем изначальные 8%: 7.96%. Это и есть эффект выпуклости в условиях неопределенности будущих процентных ставок. Если для двухлетней облигации он выражен достаточно слабо, как видно из расчетов и визуально на рисунке, то с ростом срока до погашения он будет проявляться всё сильнее:
Чем больше срок до погашения, тем выше выпуклость облигации и тем меньше будет требуемая доходность, если участники рынка ожидают хоть какой-то волатильности ставок в будущем. Разница в доходностях “без волатильности” и “с волатильностью” и есть стоимость выпуклости. Всё это приводит к тому, что чем больше ожидаемая волатильность, тем сильнее будет давление на дальний конец кривой доходности. Если участники рынка ожидают очень сильную волатильность, кривая доходности может даже приобрести сгорбленную форму, когда среднесрочные ставки будут выше, чем кратко- и долгосрочные. Об этом будет подробнее рассказано в дальнейшем, когда мы изучим биномиальные решетки применительно к оценке облигаций.
В обычных условиях эффект выпуклости прибивает дальний конец кривой вниз, так что несмотря на растущую со сроком до погашения премию за риск, кривая доходности практически выходит на плато. Этот механизм обеспечивают участники рынка, например пенсионные фонды: они эксплуатируют большую выпуклость длинных облигаций, и соглашаются приобретать их с пониженной премией.
Вообще говоря, форма кривой доходности будет определяться не только ожиданиями избегающих риска инвесторов, но и поведением спекулянтов, находящихся в постоянном поиске арбитражных возможностей. Используя непрерывное начисление процентов можно доказать следующую теорему:
Если текущая временная структура y₀(T₁), y₀(T₂), y₀(T₃) (T₁ < T₂ < T₃) является выпуклой, т.е. выполнено неравенство
y₀(T₂) ≤ a∙y₀(T₁)+(1-a)∙y₀(T₃) где a = (T₃ — T₂)/( T₃ — T₁)
то существует стратегия торговли облигациями, обеспечивающая арбитражную прибыль в случае параллельного сдвига кривой доходности.
y₀(T₂) ≤ a∙y₀(T₁)+(1-a)∙y₀(T₃) где a = (T₃ — T₂)/( T₃ — T₁)
то существует стратегия торговли облигациями, обеспечивающая арбитражную прибыль в случае параллельного сдвига кривой доходности.
Примеры выпуклых кривых доходности (согласно определению, плоская и наклонная линии тоже считаются выпуклыми), а также нормальной (вогнутой) кривой приведены на рисунках ниже:
Мы можем исследовать случай плоской временной структуры, чтобы убедиться в наличии арбитражных возможностей. Пусть у нас имеются три бескупонные облигации со сроками до погашения 5, 10 и 15 лет соответственно. Ставка одинакова для всех сроков и составляет 6%. Продадим (зашортим) 10-летнюю бумагу, и на вырученные средства приобретем короткую и длинную, таким образом у нас получатся нулевые затраты на создание позиции. Пропорцию между вложениями в 5-ти и 15-летнюю облигацию выберем так (в данном примере она составит 50% на 50% ), чтобы дюрация этого портфеля была равна дюрации 10-летки. Так мы избежим ценового риска при малых отклонениях доходности. Предположим, что ставка может вырасти или упасть на 2 п. п., либо останется неизменной. Будем удерживать нашу позицию 10 лет, вплоть до погашения среднесрочной облигации (5-летку реинвестируем под существующий на рынке процент)
На приведенном рисунке хорошо видно, что в этом случае мы накапливаем прибыль на всем протяжении удержания позиции вне зависимости от направления сдвига кривой доходности. Если же ставка не изменится, мы не получим ни прибыли, ни убытка. Общий доход не очень велик, всего около 80 базисных пунктов на единицу “вложений”, т.е. если мы продадим 10-летних облигаций на 1 млн руб., то заработаем всего 8000 руб. и это при очень серьезном движении процентных ставок. Это лишний раз подчеркивает тот факт, что выпуклость — эффект второго порядка, т.е. на нем много не заработаешь. Однако бесплатных завтраков много не бывает, тем более, что участники рынка могут легко масштабировать такую арбитражную прибыль.
Ниже также приведен график прибыли от удержания позиции на горизонте одного года в зависимости от процентной ставки, где наглядно видно, что чем сильнее отклонение доходности, тем больше арбитражная прибыль. Понятно, что в реальных обстоятельствах никто из трейдеров не будет удерживать позицию хоть сколько-нибудь долго и зафиксирует прибыль сразу после того как станет ясно, что движение ставок близко к завершению.
Таким образом, благодаря неравенству Йенсена и эксплуатации арбитражных возможностей вся кривая доходности не будет выглядеть как парабола, нарисованная Василием Олейником (см. предыдущую часть главы 3) в одном из блистательных финансовых шоу про вечно бодрствующие деньги. Безусловно, в зависимости от экономической ситуации, действий центральных банков и наличию жестко сегментированных рынков фиксированного дохода, временная структура может принимать самые причудливые очертания, но наиболее устойчивой к перипетиям судьбы останется вогнутая (нормальная) форма.
Обсуждение некоторых стратегий на рынке облигаций
В предыдущем разделе мы выяснили, что на форму кривой доходности существенное влияние оказывают три фактора: 1) мнение инвесторов о динамике будущих краткосрочных ставок 2) премия за срок до погашения и 3) эффект выпуклости (нелинейность зависимости цены облигации от ставки требуемой доходности)
Мы также упомянули некоторые арбитражные стратегии, эксплуатирующие свойства и возможную динамику кривой, что может приводить к существованию определенных типов равновесий.
Но мы до сих пор не обсуждали подробно, как та или иная форма временной структуры может повлиять на будущий доход инвестора.
I. В качестве первого приближения будем считать, что кривая доходности останется неизменной на всем сроке удержания позиции
В одной из прошлых частей мы рассмотрели пример плоской кривой и показали, что в этом случае планируемая стоимость инвестиции при ежегодном начислении процентов FV может быть через T лет рассчитана как FV = P₀(1+r)ᵀ , где r — доходность к погашению (YTM), P₀ — цена купонной облигации. Это была очень удобная форма представления, так как при данном подходе наша облигация практически не отличается от депозита. Ведь мы знаем, что если поместим 1000 руб. на вклад с ежегодным начислением процентов по ставке 10%, то через год получим 1100 руб., а еще через год — 1210. Однако в том случае, если кривая доходности не является плоской, будущую стоимость подсчитать уже не так просто.
Покажем это на примере 10-летней бескупонной облигации. Мы используем ту же временную структуру, что и в части 3 глава 2:
*Спотовая кривая на рисунке это кривая бескупонной доходности или КБД.
Тогда доходность за период владения по бескупонной облигации (например, за год) — HPR (holding period return) — будет равна соответствующей краткосрочной форвардной ставке f (а не YTM, которая для бескупонной облигации совпадает со спотовой ставкой s)
Это прямо следует из формулы
HPR = Pₙ₋₁ /Pₙ — 1 = (1+sₙ)ⁿ/(1+sₙ₋₁)ⁿ⁻¹ — 1 = fₙ₋₁,ₙ
и связано с тем, что через год облигация будет дисконтироваться уже по новой спотовой ставке. В нашем примере спотовая ставка (она же в данном случае и YTM, и эфф. доходность) для 10-летней бескупонной облигации s₁₀ равна 6.92%. Но если мы продадим эту бумагу через год, то заработаем больше, чем 6.92%, так как облигация станет уже 9-летней и ее цена будет рассчитана исходя из новой спотовой ставки s₉ = 6.83%. Наша реализованная доходность составит
HPR = (1+s₁₀)¹⁰/(1+s₉)⁹ — 1 = f₉,₁₀ = 7.72%
Если использовать приближенную формулу, то HPR для бескупонной облигации можно разложить на две составляющие: доходность к погашению (yield, YTM) и разницу спотовых ставок, умноженную на оставшийся срок до погашения, так называемый ролл-даун (roll down return) В нашем примере:
HPR ≈ s₁₀ +(s₁₀ — s₉)∙9.
То есть, даже при небольших различиях в спотовых ставках покупка длинной облигации может принести инвестору существенный доход на коротком горизонте в случае нормальной формы кривой доходности. Эта стратегия носит название “скольжение по кривой доходности” (riding yield curve) и используется трейдерами, полагающими, что за время инвестирования КБД не претерпит существенных изменений.
Если мы будем удерживать нашу облигацию дольше года, ее стоимость будет расти как
FV = P₀(1+f₉,₁₀)∙(1+f₈,₉)(1+f₇,₈)…
Однако в сам момент погашения эта стоимость будет такой же, если ее изначально рассчитать по формуле FV = P₀(1 + s₁₀)¹⁰ т.е. предположить, что кривая доходности плоская, а ставка дисконтирования равна s₁₀
На рис. ниже приводится изменение стоимости указанной облигации при неизменной форме спотовой кривой. Видно, что она нигде не совпадает с расчетом по формуле для YTM вплоть до срока погашения облигации.
Очевидно, что если мы имеем такую картину даже при неизменной кривой бескупонной доходности, то и в случае ее произвольной динамики YTM нельзя будет использовать для подсчета будущего дохода на горизонте инвестирования меньшем, чем срок до погашения.
Более того, если для бескупонной облигации мы точно знаем полный доход в момент ее погашения, — вне зависимости от того как будет вести себя кривая, — то для облигации, выплачивающей купоны, этот доход не может быть известен заранее. Ведь, для того чтобы формула FV = P0(1+r)ᵀ осталась верна в момент погашения, необходимо реинвестирование всех получаемых купонов под одну и ту же доходность r. В общем случае добиться этого результата не представляется возможным.
В качестве еще одного примера рассмотрим приобретение двухлетних облигаций с различными ставками купона. Предположим, что номинальные доходности (облигации с такими купонными ставками торгуются за номинал) для бумаг со сроком погашения 1 и 2 года равны 3% и 6% соответственно. Как и прежде, считаем, что “кривая доходности” остается неизменной. Из номинальных ставок мы можем вывести спотовые и форвардные ставки, как делали это ранее, а затем рассчитать справедливые цены для любых двухлетних облигаций и соответствующие им доходности к погашению. В таблице 1 представлены расчеты для облигаций с купонной доходностью 0%, 2%, 6%, 10%. Для корректности сравнения мы вкладываем один и тот же капитал (100) в каждую из облигаций, полученный купон инвестируем под годовую доходность (3%) и наблюдаем за ростом стоимости вплоть до погашения.
Таблица 1
На рис. ниже для наглядности построены зависимости для двух крайних случаев: ставки купона 0% и 10%.
Заметим, что в данном случае наибольший доход принесло бы инвестирование в бескупонные облигации. И это не случайность: однопериодная HPR будет максимальной именно для бескупонной облигации, если спотовая кривая возрастает. Она, как мы видели выше, равна краткосрочной форвардной ставке для этого периода. Для купонной же облигации можно показать, что HPR (за один купонный период) равна средневзвешенной по приведенным стоимостям денежных потоков форвардной ставке, т.е. будет заведомо ниже, если кривая доходности имеет строго положительный наклон.
Получается, что если инвестор с коротким горизонтом вложений предполагает, что нормальная форма кривой в ближайшие полгода не изменится, для него имеет смысл купить длинную облигацию с самым низким купоном.
Но насколько длинные облигации стоит приобретать, если форма КБД является нормальной? Может быть, самые длинные? Например, такие, для которых эфф. доходность, указанная в брокерском приложении, будет максимальной? Должна ли доходность к погашению быть единственным ориентиром при принятии решения о покупке облигаций в том случае, если КБД не является плоской, но ее форма предполагается постоянной на время удержания позиции? Ответ на этот вопрос в общем случае отрицательный.
Как мы выяснили в одной из прошлых частей, влияние выпуклости приводит к тому, что при нормальной форме КБД доходности длинных облигаций практически выходят на плато (более того, иногда дальний конец кривой может загибаться вниз, если ожидается сильная волатильность процентных ставок, т.е. нормальная форма превращается в сгорбленную)
На рис. ниже изображен как раз такой случай. Мы видим, что рост бескупонных доходностей на дальнем конце сильно замедляется, а возрастающая форвардная кривая с какого-то момента начинает убывать. Форвардная ставка, так же как и бескупонная HPR, достигает максимального значения для облигаций приблизительно 9-ти летней дюрации. При этом YTM для девятилеток будет ниже, чем, например, для 10-ти и 15-ти летних бумаг, поскольку кривая доходности остается растущей.
*Пример вогнутой кривой доходности. Форвардная кривая имеет единственный максимум.
Поведение форвардной кривой легко объяснимо, если вспомнить приближенную формулу для бескупонной HPR:
HPR = fₙ₋₁,ₙ ≈ sₙ +(sₙ — sₙ₋₁)∙(n-1)
“Прибавка” к спотовой ставке sₙ, то есть ролл-даун, будет зависеть не только от знака выражения (sₙ — sₙ₋₁), но и от произведения (sₙ — sₙ₋₁)∙(n-1) Когда рост доходностей начинает замедляться, уменьшается и спред спотовых ставок. В каком-то смысле форвардная ставка представляет собой маржинальную доходность, а форвардная кривая наглядно “высвечивает” наиболее эффективные для инвестирования участки КБД, которые затруднительно увидеть невооруженным глазом.
Таким образом, форма КБД — важный аспект, который инвесторы далеко не всегда учитывают, когда смотрят на эффективные доходности облигаций в Quik или на сайте Мосбиржи. У всего есть обратная сторона, и если в каких-то ситуациях можно повысить свою доходность, в других она может оказаться куда меньше ожидаемой. Ведь, например, в случае сильно инвертированной кривой, форма которой остается неизменной долгое время, покупка длинной облигации приведет к тому, что инвестор будет зарабатывать не положительный, а отрицательный ролл-даун при кратковременном удержании позиции, т.е. полученный прирост стоимости будет меньше, чем эффективная доходность, указанная в брокерском приложении или на сайте Мосбиржи (Напомним, что HPR > YTM в случае возрастающей кривой, HPR = YTM для плоского участка кривой и HPR < YTM в случае инверсии)
К сказанному выше можно сделать несколько замечаний
Инвестор, рассчитывающий, что форма КБД в ближайшие несколько месяцев (например, до получения следующего купона) не изменится, предпочтет выбрать такие участок кривой и ставку купона по облигации, когда HPR достигает наибольшего значения. Например, длинную бескупонную облигацию при положительном наклоне кривой доходности и, наоборот, самую короткую с любой ставкой купона при инверсии кривой. Облигации с самым высоким YTM не всегда дадут наилучший результат при краткосрочном инвестировании. Для принятия решения в отдельных случаях может понадобиться кривая форвардных ставок, так как «сглаженная» форма вогнутой КБД зачастую не позволяет заметить нужный вариант. Следует также помнить, что инверсная или сильно сгорбленная форма кривой доходности неустойчивы во времени.
Любая форма КБД, отличная от плоской, содержит возможности для арбитража, если она остается неизменной неопределенно долго (например, в случае контроля кривой центральным банком страны) И в самом деле, если кривая имеет жестко зафиксированный положительный наклон, то можно купить длинные облигации и продать (зашортить) короткие, извлекая из этой позиции безрисковую прибыль. Участники рынка в таком случае будут всегда приобретать наиболее доходные, т.е. длинные, облигации, реинвестируя полученные купоны под эту же доходность, что заставило бы взявшийся управлять формой кривой центральный банк выравнивать ее, приводя к “безарбитражной” плоской форме.
Положительный наклон кривой доходности не должен быть слишком крутым, создавая огромный ролл-даун, так как игроки рынка начнут использовать квазиарбитражные стратегии в ожидании уменьшения спреда. Рано или поздно кривая все равно начнет уплощаться и спекулянты смогут получить дополнительную прибыль, но при этом их риски состоят в дальнейшем увеличении крутизны наклона/непропорциональном росте длинного конца кривой.
Для оценки эффективности краткосрочных вложений инвестор может использовать не только КБД с сайта Мосбиржи, но и обычную кривую доходности с того же сайта, где для конкретных ОФЗ в зависимости от их дюрации построены доходности к погашению. Однако в последнем случае может иметь место купонный эффект, когда практически при одной и той же дюрации ОФЗ с разными ставками купона будут иметь различную доходность к погашению. Вообще говоря, купонный эффект принято рассматривать в контексте зависимости YTM от срока до погашения, а не дюрации. Например, купонный эффект хорошо заметен в Таблице 1, где использовались модельные облигации с одинаковыми сроками до погашения: в условиях возрастающей формы КБД чем больше ставка купона по облигации, тем меньше ее YTM. Кроме того, КБД задается единственным образом, а обычная кривая доходности из-за купонного эффекта не всегда воспринимается однозначно. Поэтому, когда указывают доходности в зависимости от дюрации, а не срока до погашения, то пытаются как бы создать прокси для КБД. При нормальной форме КБД и одном и том же сроке до погашения облигации с большей ставкой купона имеют меньшую дюрацию. При таком построении они автоматически попадают в область с более низкими YTM, и следовательно купонный эффект значительно нивелируется. Но мы отмечали ранее, что этот метод неточен и необходимо строить КБД по всем правилам для получения справедливой оценки вновь поступающих на рынок облигаций. Можно показать, что купонный эффект слабо проявляется даже для облигаций одной и той же дюрации в зависимости от соотношения ставки купона и требуемой доходности. Впрочем, далеко не всегда понятно, что именно мы наблюдаем в реальности — купонный эффект или рыночную неэффективность, содержащую арбитражные возможности, когда по какой-то причине облигация торгуется дешевле или дороже своей справедливой оценки.
II. В реальности форма кривой не остается постоянной с течением времени.
Если исключить премию за срок до погашения, то сам факт наклона кривой доходности будет говорить о том, что инвесторы ожидают изменения спотовых ставок в будущем. Мы отмечали это в прошлой части, когда обсуждали гипотезу чистых ожиданий.
В этой связи перед держателем облигации встают следующие задачи:
Определение горизонта инвестирования.
Оценка доходности на заданном горизонте инвестирования (HPR, holding period return, horizon rate of return) с учетом возможных изменений временной структуры.
Подбор стратегии, позволяющей оптимизировать HPR исходя из целевого прогноза по процентным ставкам.
Горизонт инвестирования имеет существенное значение. Инвестору, планирующему продать облигацию через месяц-другой, не нужно размышлять над проблемой реинвестирования купонов, для него важен неблагоприятный ценовой (рыночный) риск т.е. снижение стоимости облигации, вызванное ростом ставок. А если государственная облигация удерживается до погашения, то, наоборот, риск реинвестирования становится главным фактором. Этот риск является асимметричным и связан с возможным снижением ставок, т.е. необходимостью реинвестировать купоны под более низкий процент. В результате инвестор получит меньшую будущую стоимость (или общий денежный доход). Риск реинвестирования тем выше, чем больше
Срок до погашения.
Ставка купона.
Риск реинвестирования максимален для “вечных” облигаций.
Поэтому, чтобы не рассматривать риск реинвестирования, в своем анализе мы будем поначалу исходить из небольшого срока удержания позиции, составляющего не более одного купонного периода: месяц, квартал, полгода, год.
Ожидаемую (или подразумеваемую текущей спотовой кривой) через год спотовую ставку s*ₖ для срока погашения k можно получить, используя общую формулу
(1 + fₘ,ₖ)ᵏ⁻ᵐ = (1 + sₖ)ᵏ/(1 + sₘ)ᵐ положив m = 1; s*ₖ = f₁,ₖ
Ставку f₁,ₖ называют также подразумеваемой форвардной доходностью (implied forward yield) по бескупонной облигации с погашением через k лет и ее следует отличать от краткосрочной форвардной ставки fₖ₋₁,ₖ , которая представляет собой ожидаемую ставку по годичной облигации с погашением через k лет:
Для ситуации, показанной на рис. в начале главы 4.1, участники рынка полагают, что через год вся спотовая кривая сместится вверх и новая доходность к погашению (спотовая ставка), например, для 9-летней бескупонной облигации станет равной s*₉ = f₁,₉ = 7.19%
Тогда не будет разницы между удержанием 10-летней и годовой облигации — в случае ожидаемого движения кривой (в точности как на рисунке) обе бумаги принесут через год одинаковый доход в 4.5%, что легко проверить расчетами. Годовая бумага с доходностью 4.5% погасится, а десятилетка принесет
P*₉/P₁₀ − 1 = (1+6.92%)¹⁰/(1+7.19%)⁹ − 1 = 4.5%
Премию в доходностях для 10-летней и годовой бескупонных облигаций
(2.42% = 6.92% − 4.5%) “съест” просадка капитала, вызванная общим ростом ставок.
Звёздочка в обозначениях используется для новых значений переменных, возникающих после сдвига кривой доходности.
Можно показать, что положительный наклон текущей КБД “предполагает” рост доходностей, а вогнутая форма — ее уплощение в будущем. Выпуклая форма кривой доходности, наоборот, будет говорить об ожиданиях увеличения крутизны наклона кривой.
Понятно, что ожидания инвесторов оправдываются не всегда, тем более, что на текущую форму кривой влияет множество факторов помимо собственно прогноза о динамике краткосрочных ставок. Это и неизвестная премия за риск, меняющаяся со временем, и неопределенность относительно будущей волатильности процентных ставок.
Более того, оказывается, что при спокойном состоянии рынка КБД скорее всего не изменит свою форму через короткий промежуток времени, т.е. возможность заработать небольшой ролл-даун — вполне рациональное предположение, если исходить из статистических данных. Также существует парадокс: чем хуже форвардные ставки предсказывают будущие краткосрочные ставки, тем лучше они предсказывают HPR.
В целом, приближенное значение HPR за один период для n-летней бескупонной облигации можно разбить на две составляющих:
(1) rolling yield или доходность за период при неизменной кривой, равная краткосрочной форвардной ставке:
fₙ₋₁,ₙ = (a) доходность к погашению (она же текущая спотовая ставка) + (b) ролл-даун, и
(2) влияние изменения временной структуры:
c) эффект дюрации + (d) учёт выпуклости
HPRₙ ≈ fₙ₋₁,ₙ + (1+fₙ₋₁,ₙ)∙[ — Dₙ₋₁∙Δsₙ₋₁ + 0.5∙Cₙ₋₁∙(Δsₙ₋₁)²]
гдеΔsₙ₋₁ = s*ₙ₋₁ — sₙ₋₁ и s*ₙ₋₁ — новое значение спотовой ставки для момента времени спустя один период. Здесь предполагается, что изменение кривой доходности происходит мгновенно в момент времени n — 1; именно для этого момента вычисляются значения дюрации и выпуклости. Кроме того, появляется поправка (1+fₙ₋₁,ₙ), так как изменению подвергается значение Pₙ₋₁/Pₙ = (1+fₙ₋₁,ₙ)
В этом выражении s*ₙ₋₁ (и, соответственно, изменение доходности Δsₙ₋₁) — неизвестная (случайная) величина, а значит, возникает необходимость в оценке ее математического ожидания.
Если у инвестора нет определенного мнения о направлении движения ставок (т.е. матожидание E [Δsₙ₋₁] = 0), то средняя доходность за период E[HPRₙ] помимо fₙ₋₁,ₙ будет зависеть только от матожидания E[(Δsₙ₋₁)²] А оно в данном случае равно дисперсии доходности и может быть оценено, например, по данным исторической волатильности процентных ставок. Таким образом, во втором приближении для HPR к форвардной ставке добавляется стоимость выпуклости 0.5∙Cₙ₋₁∙(vol[Δsₙ₋₁])²
Эта стоимость приобретает более-менее существенное значение лишь у длинных облигаций и при высокой ожидаемой волатильности. Например, по данным за 2013-2022 гг. можно рассчитать, что для ОФЗ 10-летней дюрации ожидаемая за торговый день (только благодаря выпуклости) доходность составляет около 1 б. п. Она куда меньше торговых издержек на спред и комиссионное вознаграждение, т.е. уловить ее при внутридневной торговле практически невозможно. Однако в годовом выражении ожидаемая доходность достигает уже более 200 б. п., что могло бы послужить весомой прибавкой к капиталу инвестора, если бы о полезных свойствах выпуклости не знали все остальные. Это сакральное знание давно учтено в ценах длинных облигаций (именно поэтому, как мы помним, КБД выходит на плато с увеличением срока до погашения)
Вместе с тем, как хорошо известно, большинство трейдеров все же умеют предсказывать точное направление движения цены. Доказательства этому можно обнаружить в авторских блогах, где часто используется фраза-маркер “яжеговорил” В случае целевого прогноза именно дюрация и связанные с ее влиянием прирост/просадка капитала станут определяющим фактором, влияющим на HPR. Так, для 10 летней облигации при ожидаемом в конце периода скачке доходности в 10 б.п. потери в HPR могут составить до 100 б. п.
Оптимальный выбор бумаги прямо связан с мнением инвестора о величине и направлении изменения процентных ставок. Рассмотрим упомянутую ранее спотовую кривую из начала главы 4.1 Какговорилось в этой главе, если инвестор уверен в том, что кривая останется неизменной (и в отсутствие волатильности), он приобретет облигацию с таким сроком до погашения, для которого краткосрочная форвардная ставкой fₙ₋₁,ₙ достигает наибольшего значения. В том примере форвардная ставка, так же как и однопериодный HPR, была максимальной для облигаций приблизительно 9-ти летней дюрации. Если же кривая сдвинется ровно так, как “предсказывают” форвардные ставки, т.е. в соответствии с подразумеваемой форвардной доходностью, то все участники рынка получат одинаковый HPR = 4.5% независимо от того какую облигацию они выберут — короткую, длинную или среднесрочную. Но допустим, что проницательный инвестор считает наиболее вероятным сценарием параллельный сдвиг КБД на 25 б.п. вверх в конце года, когда он собирается закрыть свою позицию. На рис. показана зависимость ожидаемого в этом случае HPR от срочности облигации. Для бумаг любой дюрации ожидаемый HPR > 4.5%, так как прогнозная КБД лежит всюду ниже кривой подразумеваемых через год спотовых ставок. Лучший результат покажет 5-ти летняя бумага с ожидаемым HPR = 6.31%.
Чем больше согласно базовому сценарию вырастут спотовые ставки, тем меньше ожидаемый HPR и тем более короткую облигацию выберет инвестор (при нормальной форме КБД). Для сдвига величиной 75 б.п. оптимальной для покупки окажется 3-летняя бумага с прогнозным HPR = 4.92%:
Стратегии, основанные на сверхспособности предвидеть уровни процентных ставок в обозримом будущем, называются duration strategies. Сформулировать их в общем виде предельно просто. Если инвестор ожидает снижения ставок в экономике, то ему рекомендуется увеличивать дюрацию своего портфеля; если наоборот, — сокращать. Когда облигации торгуются с доходностью значительно выше среднего, можно, конечно, подумать о включении в портфель и бумаг, у которых срок до погашения гораздо больше, чем горизонт инвестирования.
Однако жизнь показывает, что следует с особой осторожностью подходить к приобретению длинных облигаций, даже если инвестор считает, что покупает ценовое “дно” Опасность приобретения долгосрочных инструментов хорошо иллюстрируется следующим примером.
В ноябре 2021 г. на страницах “крупнейшего в России сообщества трейдеров и инвесторов” было опубликовано интервью с банковским служащим, часто привлекаемым известным околорыночным блогером в качестве эксперта по бондам. В нем он посоветовал инвестору, которому денежные средства понадобятся через год, обратить внимание именно на длинные облигации, так как считал, что 8.3-8.4% на дальнем конце ОФЗ являются пиковой доходностью:
“Можно брать 7-10 лет, можно брать 2-3 года, но в последнем случае из-за возможного понижения ставки они не будут так перформиться, они будут стоять на месте. Ожидаю в следующем году общий доход 11-15% от середины и длины. Если ЦБ будет сильно повышать ставку, мы можем видеть инверсию кривой все больше и больше, но дальний конец будет реагировать не так сильно; инфляция будет в районе 4% в начале 2023”
“Поэтому как раз длина менее рискованно, чем в коротье сидеть” — заключил эксперт.
К сожалению, он ни разу не упомянул, что при тенденции растущих ставок и столь малом горизонте инвестирования безопаснее всего выбирать облигации со сроком погашения равным этому горизонту (или хотя бы флоатеры) Дальний конец может, конечно, в случае чего “реагировать не так сильно”, но дюрация обязательно сделает свое дело, и цены длинных бумаг обрушатся. События конца февраля 2022 г привели к тому, что и по сей день цены 7-10 летних ОФЗ не достигли уровней конца прошлого года, а краткосрочные держатели длинных облигаций потеряли по сравнению с банковскими вкладчиками.
А в тучные годы и при исторически низких ставках стратегия финансирования покупки длинных облигаций за счет краткосрочных заимствований напоминает продажу опционов с дальними страйками: до поры до времени все идет хорошо, и владелец долго получает свою риск-премию, но однажды наступает момент горькой расплаты.
Для повышения качества собственных прогнозов инвестору желательно внимательно следить за риторикой руководителей Центрального Банка. Если некоторое количество кварталов подряд растет инфляция и ЦБ начинает разговоры о возможном начале цикла повышения ставок, дюрацию портфеля лучше сокращать заранее: перекладываться из длинных облигаций в короткие либо флоатеры. Нужно понимать, что в такие времена флоатеры могут показаться самым невыгодным инструментом и их совершенно не захочется покупать. В начале 2021 г ставка RUONIA, являющаяся базой для расчета купона по некоторым ОФЗ-ПК была чуть выше 4%, что составляло около половины доходности надежных корпоратов. Но если проанализировать поведение цен ближних флоатеров ОФЗ-ПК 24020, 24021 в момент страшных потрясений рынка в конце февраля 2022, то их восстановление с учетом вынужденного месячного перерыва не заняло и нескольких дней. А если принять во внимание, что даже короткие облигации могут значительно просесть из-за тектонических сдвигов ключевой ставки ЦБ, то флоатеры демонстрируют ни с чем не сравнимую устойчивость и могут заменить наличные деньги для входа на рынок на самом дне.
Итак, ожидаемую инвестором за период доходность по бескупонной облигации можно разложить на 4 составляющие:
E[HPR] = YTM + ролл-даун + стоимость выпуклости + ожидаемый прирост капитала.
Аналогичную формулу можно получить и для облигации, выплачивающей купоны. Но в этом случае доходность за период в отсутствие сдвигов кривой доходности (YTM + ролл-даун = rolling yield) уже не будет равна краткосрочной форвардной ставке, как это было для бескупонной облигации. В качестве rolling yield можно взять средневзвешенное значение форвардных ставок (по приведенным стоимостям денежных потоков) но куда удобнее представить его в виде суммы текущей доходности и ролл-дауна:
Rolling yield = Coupon/P + ΔP/P, где P — цена облигации в момент приобретения, ΔP — теоретическое изменение цены в конце купонного периода при неизменной спотовой кривой.
При дальнейшем анализе возникают закономерные вопросы. Если мы всё же предполагаем сдвиг кривой доходности в конце периода, то что рассматривать в качестве “мгновенного” изменения доходности Δr? Какие брать дюрацию и выпуклость? А если у нас портфель облигаций? Казалось бы, для купонной облигации нужно использовать обычную доходность к погашению, и рассчитанные на ее основе дюрацию и выпуклость. А для портфеля облигаций — средневзвешенные по рыночной стоимости значения, как рекомендует делать большинство статей на популярных финансовых ресурсах. Но далеко не все так просто.
Во-первых, тогда как YTM единичного денежного потока воспринимается однозначно (это спотовая ставка), доходность портфеля облигаций всегда требует уточнений. Истинный YTM портфеля рассчитывается как IRR (внутренняя ставка доходности) всех денежных потоков (мы говорили об этом в самых первых частях) Хорошим приближением к данному показателю будет так называемая доходность, взвешенная по дюрации (duration weighted yield)
rₚ = Σ Pᵢ∙rᵢ∙Dᵢ / Σ Pᵢ∙Dᵢ где — Pᵢ, rᵢ, Dᵢ — цена, YTM и дюрация i-ой облигации в портфеле.
Менее точной оценкой, но более удобной для расчета является так называемая средневзвешенная доходность (market value weighted yield), когда весами выступают рыночные стоимости отдельных облигаций в портфеле. Чаще всего именно она используется в литературе:
rₚ = Σ Pᵢ∙rᵢ / Σ Pᵢ
Во-вторых, как бы нам ни хотелось, мы не сможем ограничить наш анализ использованием только одной агрегированной переменной — доходности к погашению. Ведь если её достаточно, то незачем было бы возиться с rolling yield, сдвигами кривой доходности и так далее. Мы могли просто взять известную формулу, которая связывает YTM и цену облигации, прикинуть, что через полгода требуемая доходность изменится на столько-то базисных пунктов и прямо рассчитать ожидаемый за период доход (усредненный HPR). Проблема заключается в надежности/уместности такого подхода. Как взвесить шансы того или иного значения Δr? На что опираться при построении прогноза, на какую статистику? С одной стороны, точно такое же изменение YTM для конкретного портфеля (как бы мы его ни считали) можно получить массой способов, при различных сценариях движения спотовой кривой. С другой, после сдвига кривой доходности неодинаковые по составу портфели скорее всего продемонстрируют разные результаты.
Для оценки ожидаемой доходности правильным методом будет использовать в качестве инструмента всю спотовую кривую, как мы это делали ранее при расчете стоимости облигаций, портфелей и вообще любых денежных потоков с разными сроками поступления. Кроме того, мы должны переопределить понятия дюрации и выпуклости. При этом важно подчеркнуть, что для анализа необходимо применять именно спотовую кривую, т.е. КБД, а не “обычную” кривую доходности (зависимость процентных ставок от срока до погашения для торгующихся на рынке купонных облигаций одинакового кредитного качества)
В известной книге Ф. Фабоцци “Рынок облигаций. Анализ и стратегии” эти два вида кривых зачастую смешивают, что может привести к неверной интерпретации полученных результатов. Так, в главе 22 “Стратегии активного управления портфелем облигаций” при обсуждении сдвигов кривой приводится модельный пример для трех торгующихся за номинал купонных облигаций и изучается поведение разных портфелей, составленных из этих бумаг. Под кривой доходности там понимается номинальная кривая (par yield curve) Для такой кривой ставки купонов по облигациям равны их доходности к погашению. Автор рассматривает разные сценарии движения этой кривой через полгода удержания позиции. Например, он считает, что если доходность для каждой бумаги осталась прежней, то это означает неизменность кривой доходности. А если доходности изменились на одинаковую величину, то кривая сдвинулась параллельно. В известных материалах для подготовки к экзаменам CFA Kaplan Schweser допускаются схожие предположения: считается, что если n-летняя купонная облигация через год торгуется с той же доходностью, какая была у (n-1)- летней облигации за год до этого, то кривая доходности не изменилась. Это не совсем корректно и читателю важно понимать почему.
Допустим, текущая номинальная кривая доходности для сроков погашения {1, 2, 3} представлена структурой {3%, 6%, 8%}. Ей соответствует спотовая кривая со структурой {3.000%, 6.093%, 8.257%} Пусть у инвестора есть 3-х летняя облигация A со ставкой купона и YTM = 8% и двухлетняя облигация B со ставкой купона и YTM = 6%; обе они торгуются за номинал 1000 руб. Если через год, когда A станет двухлетней, а ее YTM по условию составит 6%, то она уже не будет торговаться за номинал, ведь у нее другая купонная ставка, чем у облигации B. Более того, выпущенная через год новая двухлетка C, торгующаяся за номинал, не будет иметь тот же YTM = 6%, что и облигация A, так как имеет место купонный эффект, который много раз обсуждался ранее (облигации с одинаковыми сроками до погашения, но разными купонными ставками, должны иметь различные доходности к погашению, если кривая доходности не является плоской) В данном примере YTM и купонная ставки у облигации C будут равны 6.122%. Теоретическая спотовая кривая в этом примере обязательно сдвинется: новые ставки бескупонной доходности для сроков {1, 2} станут равны {3%, 6.220%}.
Кривая доходности в действительности останется неизменной лишь тогда, когда через год все вновь выпущенные облигации будут торговаться с той же доходностью и по той же цене, какие наблюдались за год до этого. После долгой разлуки инвесторы вернулись на рынок и их посетило déjà vu. А это возможно только в случае если бумаги имеют одинаковую ставку купона, т.е. аналогичны по всем характеристикам, кроме срока до погашения. Бескупонные облигации отвечают этим условиям и соответствующая им кривая доходности (КБД, спотовая кривая) будет корректным инструментом анализа.
Всё это достаточно тонкие моменты, а погрешности малы, и, чтобы не углубляться в скучные детали, инвестору нужно просто запомнить: всегда и везде использовать КБД, тем более что исторические данные, необходимые для численного исследования сценариев, доступны на сайте ЦБ РФ. В данном цикле статей под кривой доходности, если прямо не указано обратное, мы всегда подразумеваем спотовую кривую.
Обычно выделяют несколько типов изменения спотовой кривой: параллельный сдвиг, изменение наклона и изменение кривизны. Примеры таких трансформаций приведены на рисунке:
В частности, параллельный сдвиг происходит тогда, когда спотовые ставки изменяются на одну и ту же величину. Если ставки по коротким облигациям вырастут сильнее, чем по длинным, говорят об уплощении (уменьшении наклона) КБД, и так далее. Понятно, что реальное движение кривой представляет собой некоторую комбинацию всех указанных типов смещений. У инвесторов и аналитиков сложилась своеобразная классификация этих типов: {bear/bull} {steepening/flattening}; positive/negative butterfly
Например, медвежье уплощение (bear flattening) — движение спотовой кривой вверх с одновременным уменьшением наклона. Положительный баттерфляй (positive butterfly) связан с уменьшением кривизны временной структуры, т.е. она становится менее сгорбленной. Если при этом кривая сдвигается вверх, то короткие и длинные ставки растут быстрее, чем среднесрочные. При движении кривой вниз всё происходит с точностью наоборот: среднесрочные ставки снижаются сильнее.
Обозначим доходности по коротким, среднесрочным и длинным облигациям как YTM(S), YTM(L), YTM(L) соответственно. Наклон кривой доходности принято измерять спредом кривой доходности:
yield spread = YTM(L) — YTM(S)
а ее изгиб спредом “баттерфляй”:
butterfly spread = — YTM(S) + 2∙YTM(M) — YTM(L)
В зависимости от целей исследования могут выбираться разные значения срочности облигаций для спредов: 2 — 10, 2 — 30, 0.25 — 5 — 10, 2 — 10 — 30 и т. д.
Раз уж мы отошли от использования YTM и его приращений при оценке ожидаемой доходности, нам следует уточнить понятие дюрации (модифицированной дюрации) для портфеля облигаций. Будем считать, что дюрация, как мера ценового риска, это чувствительность стоимости P портфеля к параллельному сдвигу КБД. Пусть все спотовые ставки мгновенно изменились на одну и ту же величину Δs. Тогда определим дюрацию портфеля Dₚ следующим образом:
Dₚ = — 1/P ∙ ΔP/Δs
Поскольку портфель можно рассматривать как совокупность бескупонных облигаций (рассматривая отдельно купоны и номиналы входящих в него бумаг), то легко показать, что определенная таким образом дюрация будет равна средневзвешенному значению дюраций составляющих его элементов. Если xᵢ — стоимость i-го актива в портфеле, то P = Σ xᵢ, ΔP = Σ Δxᵢ, где Δxᵢ —изменение стоимости i-го актива, Dᵢ = — 1/xᵢ ∙ Δxᵢ/Δs. Поэтому Dₚ = Σ xᵢDᵢ/P Данное равенство примерно выполняется и в случае, если в качестве xᵢ и Dᵢ взять цены и модифицированные дюрации самих облигаций (без разделения на купоны и номинал) Это особенно удобно, так как дюрации указаны во многих трейдерских приложениях и на сайте Мосбиржи (там нужно выбирать модифицированную дюрацию), т.е. их не нужно вычислять самостоятельно. Важно в данном подходе помнить две вещи:
варьируется вся спотовая кривая, а не YTM портфеля.
временная структура сдвигается параллельно.
В уже упомянутой книге Ф. Фабоцци “Рынок облигаций. Анализ и стратегии” при определении дюрации используется сдвиг обычной кривой доходности. В некоторых других своих работах Фабоцци говорит о сдвигах спотовой кривой. Определенная так или иначе дюрация портфеля всё равно будет равна средневзвешенной дюраций отдельных денежных потоков/облигаций, так как существенно только то, что доходности — будь это спотовые ставки или YTM купонных облигаций — изменяются на одну ту же малую величину. И всё же инвестору желательно использовать единый подход.
На рис. ниже изображены две модельные кривые: КБД (спотовые ставки) и соответствующая ей (безарбитражная) кривая доходности для облигаций со ставкой купона 20%. Ставка нарочно взята высокой, чтобы доходности реально торгующихся облигаций заведомо попадали в область между кривыми. Портфель инвестора представлен тремя облигациями, две из которых имеют относительно низкий купон по сравнению с третьей (8-ми летней) Этот портфель инвестор выбирает самостоятельно и может считать набор из 3-х точек на рис. своей личной “кривой доходности” Но параллельный сдвиг этой “кривой” не означает, что и любая другая комбинация точек внутри области, соответствующая произвольному портфелю, сдвинется параллельно, или наоборот. Инвестору могут быть не известны статистические свойства и корреляции доходностей выбранных им облигаций и его портфель не должен быть универсальным бенчмарком для всех остальных.
Поэтому в своем определении дюрации портфеля мы и останавливаемся на КБД. Аналогичные рассуждения при параллельном сдвиге спотовой кривой можно провести и для выпуклости. Выпуклость портфеля будет равна средневзвешенному значению выпуклостей составляющих его облигаций.
Как мы уже упомянули, изменение формы спотовой кривой бывает и другим — например, ее наклон может увеличиваться так, что короткие ставки снижаются, а длинные растут. Такая возможность приводит к структурному риску или риску формы кривой доходности. В этой ситуации используют так называемые частные дюрации (partial durations, key rate durations). Для их вычисления на спотовой кривой выделяют несколько точек, обозначаемых как ключевые ставки (key rates) Чаще всего они выбираются для характерных сроков до погашения, аналогично тому, как ЦБ и Мосбиржа разбивают КБД: 0.25, 0.5, 1, 2, 3, 5 и т.д. лет.
На рис. ниже приведена Кривая бескупонной доходности государственных облигаций, построенная по данным за 18 ноября 2022.
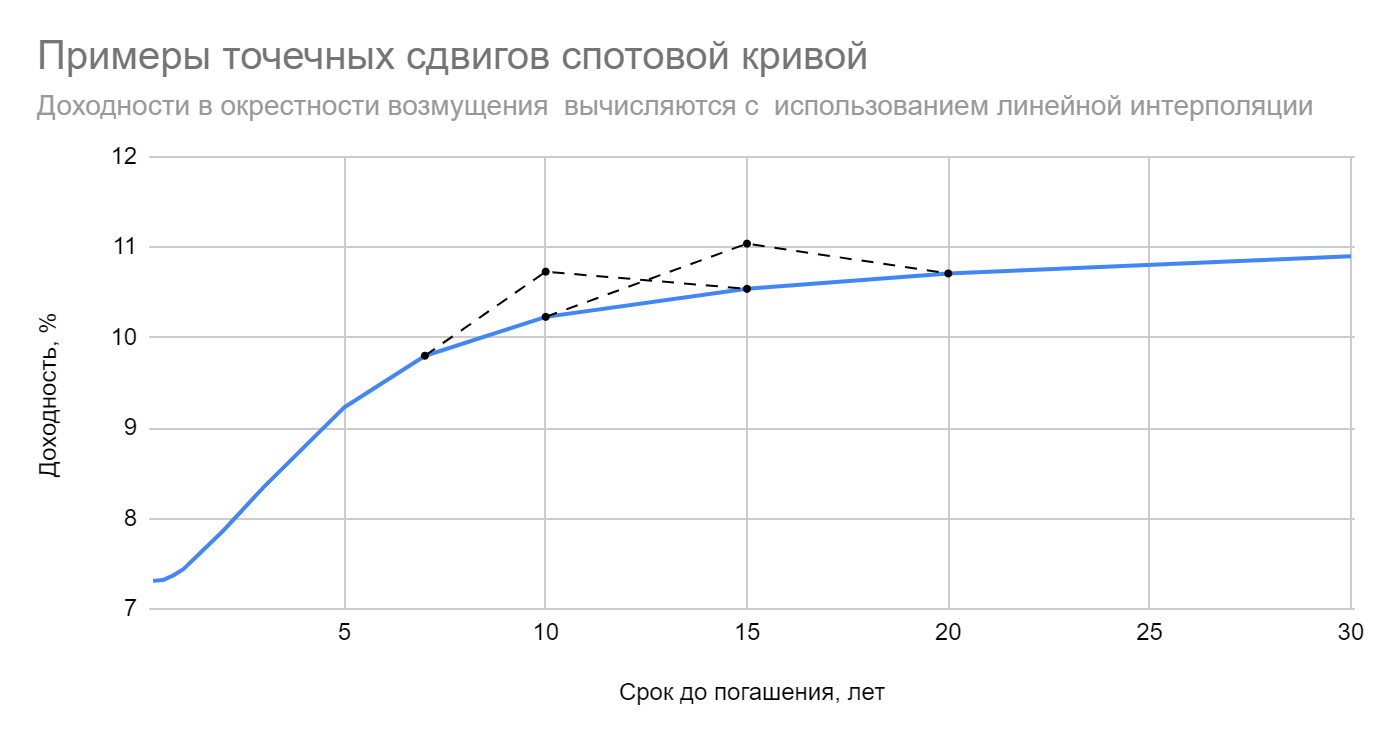
Если, например, сдвинуть 10-летнюю спотовую ставку на Δs₁₀, частная дюрация для этой точки кривой рассчитывается так:
D₁₀ = — 1/P ∙ ΔP₁₀/Δs₁₀, где ΔP₁₀ — изменение стоимости портфеля в результате этого сдвига.
Сумма всех частных дюраций будет равна дюрации портфеля (как мы ее определили выше для параллельного сдвига кривой) поскольку для точек, соседних с точкой сдвига, используется линейная интерполяция. Если все Δsᵢ = Δs, графическая сумма прямых в любой точке даст такое же значение сдвига, что эквивалентно параллельному смещению кривой.
В качестве примера рассмотрим некоторый портфель с частными дюрациями [D₀.₂₅, D₀.₅, …, D₃₀], соответствующими 12-ти срокам до погашения (какие обычно использует ЦБ РФ): [0.25, 0.5, …, 30] Допустим, что КБД повернулась относительно точки с абсциссой 7 лет так, что для каждого
i = 0..11: sᵢ = δ∙(—3.5+ i∙0.5).
На рис показано изменение формы спотовой кривой для δ = 25 б.п.:
Тогда приближённое изменение стоимости портфеля будет равно
ΔP/P = —[D₀.₂₅∙(— 3.5∙δ) + D₀.₅∙(— 3∙δ) + … + D₃₀∙(+2∙δ)]
Всё бы хорошо, но считать 12 отдельных частных дюраций вместо одной модифицированной — работа довольно утомительная (возможно, придется использовать программное обеспечение) Конечно, такой набор позволит рассчитать огромное количество различных сценариев движения кривой, но далеко не все из них будут типичными. В этой связи возникает вопрос: какие трансформации КБД разумно исследовать при составлении прогноза? Справедливо ли исходить из того, что процентные ставки скачут хаотично? Или их влияние на стоимость портфеля можно свести к небольшому ряду факторов?
По счастью, доходности ОФЗ не изменяются совсем уж произвольно и независимо друг от друга. В каком-то смысле вся КБД напоминает упругий прутик, имеющий собственные частоты: ставки по облигациям с близкими сроками до погашения обладают высокой положительной корреляцией.
Согласно историческим данным по бескупонным доходностям ОФЗ за 2013-2022 гг. можно составить матрицу этих корреляций:
Видно, что степень взаимосвязи между ставками любой срочности составляет не менее 75%, что и позволяет рассматривать КБД как единое целое. Трудно представить ситуацию, когда, например, 3-летние ставки выросли на 100 б.п., а 5-летние упали на ту же величину. Скорее всего они “потянутся” вслед за соседками.
Для снижения размерности взаимосвязанных данных без существенной потери информации широко используется метод главных компонент. Он позволяет уменьшить число переменных, выбрав самые изменчивые из них. Его математическая идея довольно проста: это создание новых переменных (как линейной комбинацией старых) таким образом, чтобы первые из полученных переменных впитали в себя практически всю изменчивость. Первая главная компонента должна иметь максимальную выборочную дисперсию. Вторая главная компонента подбирается так, чтобы с одной стороны она была не коррелирована с первой, а с другой также имела максимальную выборочную дисперсию из возможных; и так далее. Данный процесс чем-то напоминает последовательное выделение сигнала из шума и позволяет в случае измерения рисков смещения КБД свести число основных факторов к двум или трём.
На рис. ниже изображены первые три главные компоненты для приращений бескупонных доходностей ОФЗ по данным за 2013-2022 гг.
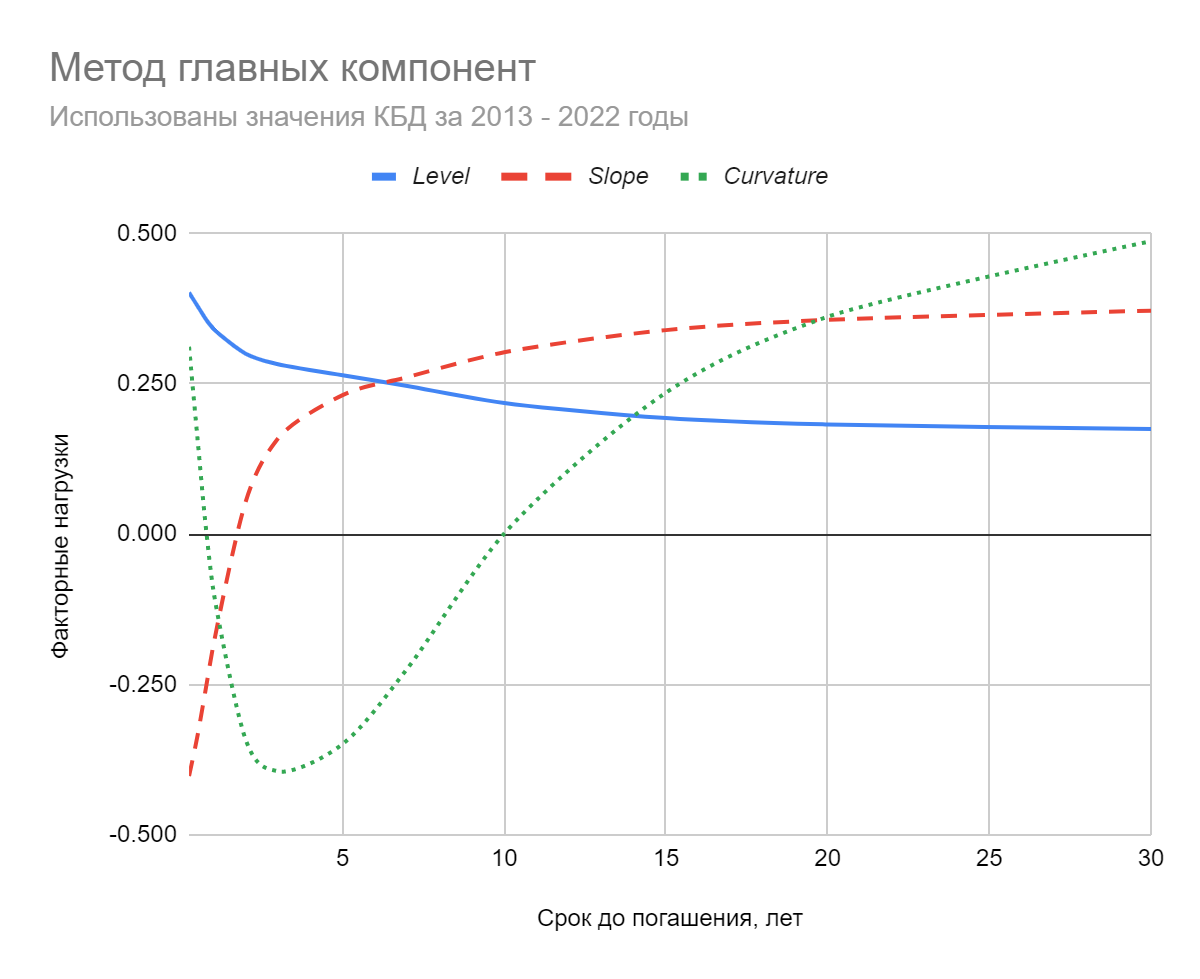
Из рисунка видно, что первая главная компонента PC1 (level) примерно соответствует параллельному сдвигу КБД, вторая PC2 (slope) — отвечает за наклон кривой, а третья PC3 (curvature) связана с изгибом КБД. Из данных за 2013-2022 гг. также следует, что PC1 объясняет почти 85% всей дисперсии, PC2 — 9%, а PC3 — 4%. Общая дисперсия, приходящаяся на первые три главные компоненты составляет около 98%
Говоря простыми словами, подавляющая часть движений КБД с достаточной для практических целей точностью может быть аппроксимирована комбинацией первых трёх факторов. Т.е., вполне естественным будет, например, прогноз: КБД как целое сдвинулась вверх, стала более плоской, а ее кривизна уменьшилась. А значит, жизненные наблюдения трейдеров и аналитиков, использующих описанную ранее классификацию — bull/bear/flattening/steepening/butterfly — имеют под собой твёрдую статистическую основу.
Кроме того, указанные три видоизменения кривой не вполне независимы друг от друга. При сдвиге спотовой кривой вверх она имеет тенденцию уплощаться и уменьшать кривизну. И, наоборот, когда ставки в целом снижаются, наклон КБД увеличивается и она становится более “сгорбленной” Так происходит потому, что краткосрочные ставки обычно показывают большую волатильность, чем долгосрочные: при любом сдвиге кривой короткие ставки стремятся “опередить” длинные. Это видно и по графику для PC1 — кривая факторных нагрузок для небольших сроков до погашения загибается вверх; при одинаковой волатильности ставок линия была бы горизонтальной.
Таким образом, метод главных компонент позволяет свести число анализируемых факторов до трёх и мы можем ввести новые меры риска для портфеля — факторные дюрации:
Dⱼ = — 1/P ∙ ΔP/Δθⱼ
где θ₁, θ₂, θ₃ — факторы, отвечающие за сдвиг, наклон и кривизну соответственно.
Увеличение первого фактора θ₁ приводит к тому, что доходности для различных сроков вырастут примерно на одну и ту же величину. Повышение θ₂ означает, что краткосрочные ставки снизятся, а долгосрочные вырастут, т.е. спред кривой доходности увеличится и т.д. Таким образом, факторная дюрация D₁ аналогична определенной выше модифицированной дюрации портфеля, а D₂ и D₃ — носят характер чувствительности к изменению спреда кривой доходности и к спреду “баттерфляй”.
Факторные дюрации обладают тем же замечательным свойством, что и обычные: факторная дюрация портфеля равна средневзвешенному значению факторных дюраций составляющих его активов.
Теперь, используя описанный выше факторный подход, можно упростить выражение для примерного изменения стоимости портфеля в результате общего сдвига КБД:
ΔP/P = —D₁∙Δθ₁ — D₂∙Δθ₂ — D₃∙Δθ₃
Когда мы обсуждали стратегии на базе ожидания изменения общего уровня процентных ставок в экономике (duration strategies), то не придавали большого значения тому, облигации какой срочности входят в состав портфеля. Фактически, мы просто рассматривали конкретную дюрацию и регулировали ее согласно прогнозам о направлении движения ставок. Внимательный инвестор быстро обнаружит, что одну и ту же дюрацию при фиксированном размере капитала можно получить разными способами. Один из них, например, — вложить всю сумму в облигации с близкими сроками до погашения. Альтернативой будет приобрести бумаги различной срочности, разместив в них те же средства в определенной пропорции, чтобы получить такую же дюрацию, как и в первом случае. На практике состав портфеля может быть самым пёстрым, но чаще всего используется три основных типа:
1) bullet (“буллетный”) 2) barbell (“барбелл”) и 3) ladder (“лестничный”)
Они схематично изображены на рисунке и не требуют особых пояснений.
В “буллетном” портфеле используются облигации, у которых срок до погашения концентрируется вокруг одной даты. У “барбелла”, наоборот, эти сроки сильно разнесены. “Лестница” напоминает аннуитетные платежи: в портфеле примерно в равной пропорции присутствуют облигации для всех сроков до погашения. В источниках это равенство пропорций трактуется по-разному: некоторые, как Фабоцци, пишут, что это одинаковое количество бумаг — т. е., например, 10 облигаций сроком в один год, столько же двухлеток и так далее. Другие авторы говорят о равенстве денежных вложений, т.е. стоимостной оценке: вложить 10 тыс. руб. в годовые, столько же в двухлетки и т.д. О различиях этих двух подходов мы поговорим позднее, но заметим, что они совпадают, если облигации приобретены за номинал.
Методы управления портфелями фиксированной дюрации носят название стратегий кривой доходности (yield curve strategies, yield curve trades with a neutral duration view) Они сосредоточены на возможности извлечения прибыли из деформаций КБД для комбинаций портфелей, имеющих одинаковую стоимость и дюрацию, но разные выпуклость и чувствительность к непараллельным сдвигам. Пример такой комбинации — стратегия “баттерфляй”, т.е. покупка “барбелла” и продажа “буллета” Она имеет в силу построения нулевые затраты и при определенных движениях КБД может принести некоторый доход.
Если мы рассматриваем мгновенные изменения нормальной (возрастающей) кривой доходности, т.е. сразу после покупки облигаций, то при малых параллельных смещениях эти три портфеля сработают примерно одинаково, поскольку у них одни и те же дюрация и стоимость. Выпуклости портфелей однако различны; их можно ранжировать по возрастанию: “буллетный” < “лестничный” < “барбелл” В силу этого при относительно больших параллельных сдвигах КБД лучший результат покажет “барбелл”: по сравнению с остальными его стоимость при снижении ставок вырастет больше и упадёт меньше при их росте. Поэтому ожидающий сильного движения трейдер может реализовать стратегию “баттерфляй”, чтобы получить доход вне зависимости от направления движения ставок. Потенциальный заработок тем выше, чем больше сдвиг и чем менее вогнутой (более выпуклой) является спотовая кривая (о различных формах кривой подробнее говорилось в этой главе)
Влияние формы КБД на результативность данной стратегии нельзя недооценивать. Дело в том, что средневзвешенная доходность “барбелла” всегда ниже, чем у “буллета” той же дюрации и стоимости, если КБД имеет нормальную форму. Мы уже обсуждали в прошлых частях, что именно такая форма препятствует арбитражу в стратегии “баттерфляй” Для реализации своего преимущества “барбелл” должен преодолевать эту “нехватку” доходности. Более того, если КБД остается неизменной продолжительное время, однопериодный HPR “буллетного” портфеля будет выше, чем у “барбелла”, т.к. эффект большей выпуклости “барбелла” со временем истощается (продолжая наши аналогии с деривативами, ситуация напоминает тета-распад стоимости опциона, если базовый актив остается без движения) А это значит, что для сохранения прибыльности стратегии “баттерфляй” понадобятся еще более серьезные сдвиги КБД в конце срока удержания позиции.
В следующем примере мы используем уже привычную временную структуру из прошлой части:

дальнейшие выкладки могут показаться слишком подробными, но они полезны для понимания механизма расчетов и навыков работы с таблицами
Допустим, мы вложили 100 д. е. в покупку 5-летних бескупонных облигаций и составили таким образом “буллетный” портфель (обозначим его латинской буквой B) Средневзвешенная доходность портфеля B равна 5-летней спотовой ставке, т.е. y(B) = 6.164% При ежегодном начислении процентов его модифицированная дюрация D(B) = 5/(1+y(B)) = 4.71 Построим эквивалентный по дюрации портфель “барбелл” из облигаций A и С сроками до погашения в 1 год и 10 лет. Для этого нам придется решить простое уравнение:
D(B) = D(A)∙x + D( C)∙(1-x)
где дюрации облигаций A и С равны соответственно D(A) =1/(1+4.5%) = 0.957; D( C) = 10/(1+6.918%) = 9.353
Из уравнения получим веса облигаций A и С в “барбелле”: x = 0.553 (вес А), 1-x =0.447 (вес C) Иными словами, в облигацию A мы вложим 100∙x = 55.3 д. е., а в С — 100∙(1-x) = 44.7 д. е. Легко проверить, что средневзвешенная дюрация “барбелла” равна дюрации “буллета”, а стоимости портфелей совпадают. Средневзвешенная доходность “барбелла” будет ниже, чем у “буллета”: 5.581% против 6.164%. Эти средневзвешенные доходности, конечно, не определяют ожидаемые через год HPR портфелей, но позволяют их качественно сравнить: если y₁ < y₂, то и НРR₁ < HPR₂ (при допущении, что КБД не изменится)
“Номинальные” стоимости облигаций (face values) легко получить с помощью формул из Excel или Google Таблиц. Например, FV(B) = FV(6.164%, 5, 0, — 100) = 134.86. Т.е., вложив сегодня 100 д.е. в облигацию B, через 5 лет мы получим 134.86 д.е. Эти стоимости нужны для дальнейшей оценки судьбы портфелей. Если все спотовые ставки после составления позиции мгновенно увеличатся на 100 б.п., то стратегия “баттерфляй” принесёт пусть и скромную, но прибыль:
PV(5.5%, 1, 0, —FV(A) ) + PV(7.918%, 10, 0, —FV( C) ) — PV(7.164%, 5, 0, —FV(B) ) = 0.08 или 8 б. п. от суммы вложенного.
Но если КБД не изменится по прошествии года, трейдер будет вынужден зафиксировать убыток от стратегии:
FV(A) + PV(6.829%, 9, 0, —FV( C) ) — PV(5.878%, 4, 0, —FV(B) ) = —1.38
А для того чтобы “баттерфляй” через год вышел в положительную зону, понадобится параллельный сдвиг КБД уже не менее 200 б. п.
Сходный анализ можно провести и для непараллельных сдвигов кривой доходности. Если кратко суммировать итоги, то в конце удержания позиции для спотовой кривой нормальной формы:
При небольшом параллельном сдвиге буллетная стратегия предпочтительней, но при достаточно сильном смещении “барбелл” покажет себя лучше
При уплощении кривой (уменьшении спреда доходности) портфель “барбелл” всегда переигрывает “буллет”
При росте наклона кривой доходности “буллетная” стратегия предпочтительней, если увеличение спреда достаточно велико
Увеличение спреда “баттерфляй” повышает привлекательность стратегии “барбелл”, а его уменьшение — “буллетной”
“Лестничный” портфель во всех случаях покажет промежуточные результаты между “буллетом” и “барбеллом”
Следует подчеркнуть, что стратегии кривой доходности:
а) Требуют при составлении портфелей придерживаться одной дюрации, что имеет смысл в случае, если инвестор следует определенному индексу или заинтересован в хеджировании текущей позиции б) Подразумевают короткие продажи (шорт) облигаций, возможность чего для большинства инвесторов недоступна. В этом могли бы помочь фьючерсы на корзину ОФЗ, но они куда-то подевались из стаканов и когда вновь появятся неизвестно. Более того, для неопытного инвестора использование фьючерсов не целесообразно. Фьючерсы на облигации, тем более на корзины, сложнее обычных и их ценообразование не всегда прозрачно в) Если и когда приносят доход, то его размер относительно невелик, а риски существенны.
Использование чистых портфельных стратегий (только “барбелл” или “буллет”) далеко не всегда даст нужный результат, среди них трудно выявить победителя. Когда нам говорят, что вот этот портфель ведёт себя лучше при прочих равных, чем другой, нам нужно проверить, не стоит ли изменить эти “равные”, прежде чем выбрать “хороший” портфель. Зачем строить “барбелл” при уплощении кривой, если ожидается, что ставки при этом пойдут вверх? Возможно, правильнее будет снизить дюрацию портфеля. Существует ли наилучшая стратегия при всём разнообразии возможных сценариев? Такая стратегия на все случаи жизни общеизвестна и носит имя М. Орловского — сидеть в кэше и ждать у моря погоды. Инвестору придется сформировать целевой прогноз, чтобы составить оптимальный портфель. Отдельно стоит отметить ситуацию с уплощением кривой — при одновременном движении КБД вниз “барбелл” однозначно предпочтительнее буллета, однако как назло, именно при снижении ставок КБД имеет тенденцию к увеличению, а не уменьшению своего наклона.
В заключение этого раздела представляем анимацию, описывающую динамику КБД за 2013-2022 г.г. Визуальный анализ зачастую позволяет выявить какие-то характерные закономерности, сделать важные наблюдения, да и вообще как-то успокаивает.
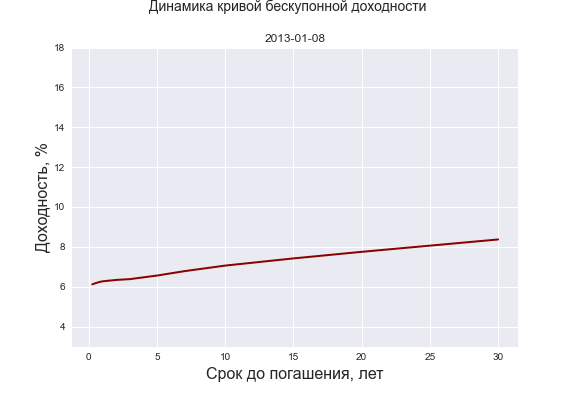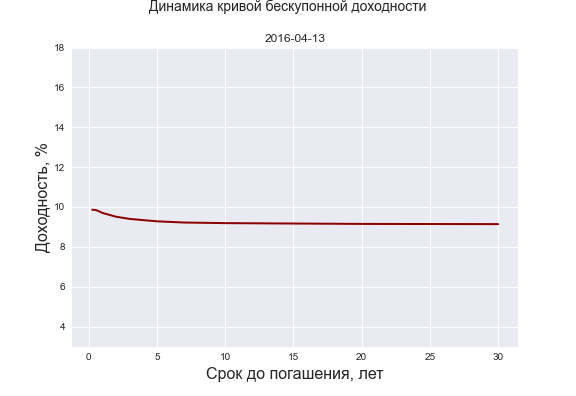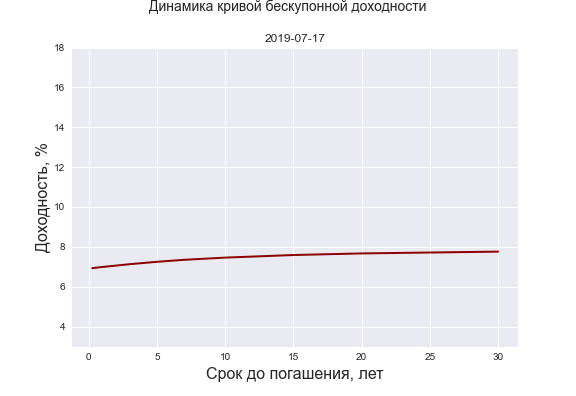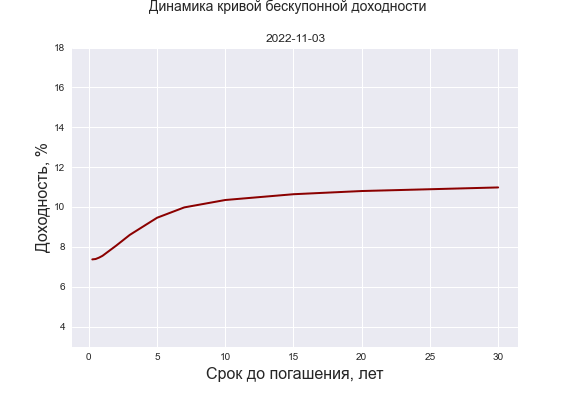
Также публикуем код в Python для импорта данных по значениям КБД и ключевой ставки с сайта ЦБ РФ, который будет полезен инвесторам для проведения самостоятельных исследований в области инструментов процентного дохода.
В следующем разделе мы вкратце обсудим политики управления портфелями облигаций, если горизонт инвестирования составляет свыше одного купонного периода.
Прежде чем перейти к обсуждению долгосрочных стратегий на рынке облигаций, используем рассмотренный в прошлом разделе подход на примере конкретных ОФЗ различной дюрации.
Допустим, 01 июня 2022 г. инвестор решил приобрести портфель облигаций стоимостью 100 тыс. рублей и собирается удерживать его не более полугода. Он наблюдает текущую форму КБД, которая всё еще остается инвертированной, хотя после сроков до погашения в 3-5 лет достаточно сильно уплощена (зеленая сплошная линия на рисунке):
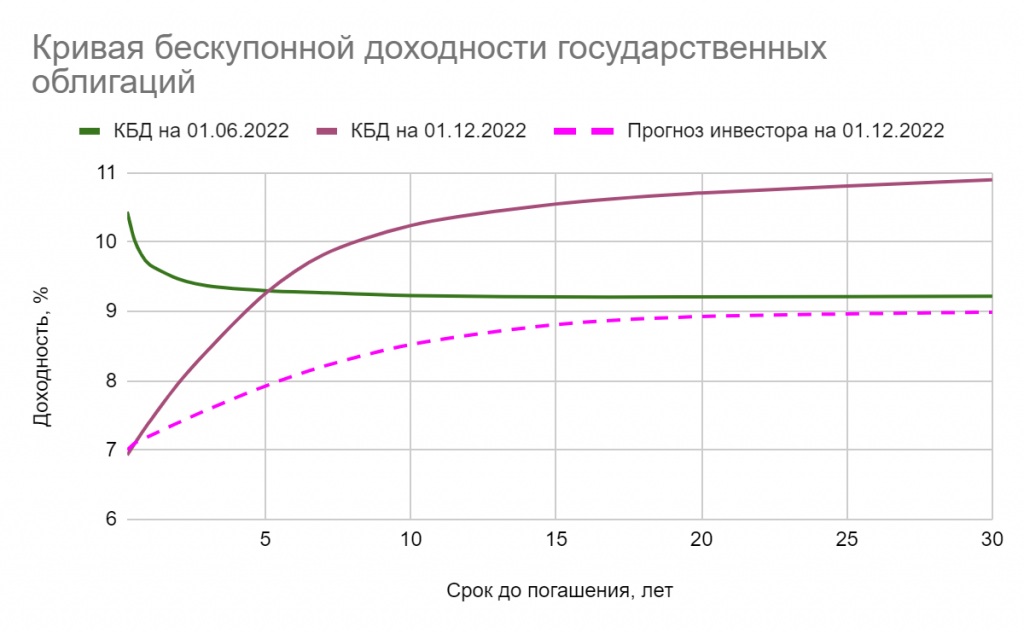
Инвестор знает, что с апреля Банк России высокими темпами снижал ключевую ставку и ожидает продолжения данной политики, по крайней мере, в течение ближайших 6-ти месяцев. Вместе с тем он достаточно консервативен в оценке поведения долгосрочных ставок и считает, что они снизятся не более чем на 50-70 б.п. Говоря иными словами, инвестор рассчитывает, что КБД через полгода примет нормальную форму в основном за счёт снижения краткосрочных ставок (прерывистая линия на рисунке) И это вполне разумный прогноз, учитывая сложившуюся на рынке ОФЗ ситуацию и политическую обстановку в стране и мире: острая фаза кризиса позади, наступил период относительной стабилизации.
По каким-то своим причинам инвестор решает приобрести портфель с дюрацией около 4-х лет и делает выбор между “барбеллом”, составленным из ОФЗ 26211, 26240, и “буллетом” — ОФЗ 26212. Модифицированная дюрация “буллета” на дату 01.06.2022 равна 4.36 лет. В компоненты сопоставимого по дюрации “барбелла” необходимо вложить почти равное количество средств: ≈ 50 тыс. рублей в каждую бумагу (точный вес ОФЗ 26211 в “барбелле” 0.498) В таблице ниже приведены данные по цене, ставке купона, доходности и мод. дюрации для указанных облигаций:
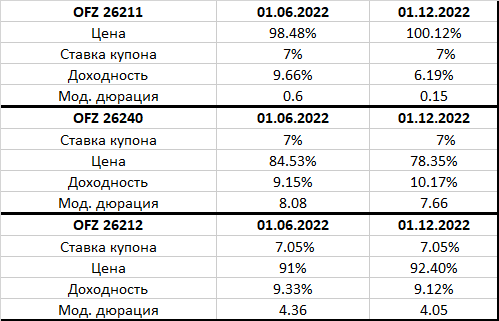
Для оценки прогнозного HPR на горизонте полугода инвестор пользуется “методом последовательных приближений”:
В нулевом приближении HPR совпадает с текущей доходностью и равен отношению купона (НКД) к цене облигации. В этом случае предполагается, что покупка и продажа бумаги происходят по одной цене. Текущая доходность аналогична доходности краткосрочного банковского вклада, т.е. мы считаем, что КБД плоская и неизменна во времени. Для “буллета” ОФЗ 26212 текущая доходность в годовом выражении составит 7.05%/91% = 7.75% (или 3.875% за полугодие) Заметим, что точные даты выплаты купонов при этом не важны, так как если мы приобретаем облигацию в межкупонный период, то сразу уплачиваем продавцу НКД, а затем получаем купон и НКД при продаже. Для “барбелла” можно рассчитать средневзвешенную текущую доходность, она окажется равной 0.498⋅7%/98.48% + 0.502⋅ 7%/84.53% = 7.7%.
В первом приближении к текущей доходности прибавляется roll down, т.е. теоретическое относительное изменение цены облигации (ΔP/P) при неизменной форме КБД. Roll down для купонной облигации бывает как положительным, так и отрицательным. Бумага может торговаться с дисконтом или премией, но с уменьшением срока до погашения ее цена стремится к номиналу. В случае инверсии КБД раньше поступающие будущие денежные потоки дисконтируются по более высоким ставкам, что объективно уменьшает roll down. Например, для ОФЗ 26240 roll down на 01.06 был отрицательным. Полученное уточненное значение для HPR называется rolling yield. Для “буллета” rolling yield равен (текущая доходность плюс roll down) 7.75% + 2⋅(916.85-910)/910 = 7.75% + 1.51% = 9.26%. Мы умножили последнее слагаемое на 2, чтобы указать величину roll down в годовом выражении, так как исследуемый период — полугодие. Средневзвешенный rolling yield “барбелла” составит 7.7% +2⋅[0.498⋅(995-984.8)/984.8 +0.502⋅(841.6-845.3)/845.3] = 7.7% + 0.6% = 8.3% годовых, что почти на 100 б.п. ниже, чем у “буллета” Подробные расчёты цен облигаций для различных форм КБД приведены в приложенном файле Excel. Значения бескупонных доходностей в точках, отличных от “канонических” сроков до погашения, получены методом линейной интерполяции. Для упрощения вычислений использовались непрерывные ставки: yᵢ = ln(1+rᵢ), где rᵢ — обычные ставки КБД с ежегодным начислением. В этом случае все денежные потоки дисконтируются как Cᵢ⋅exp(-yᵢ⋅Tᵢ), где Cᵢ — будущий денежный поток, а Tᵢ — время, оставшееся до его получения.
В последнем приближении инвестор делает прогноз о расположении и форме КБД спустя полгода. Далее он рассчитывает частные или факторные дюрации и выпуклости портфелей на горизонте инвестирования (01.12.2022) для окончательной корректировки HPR. Допустим, в качестве независимых факторов инвестор рассматривает 1) параллельное смещение КБД, 2) спред доходности для bull steepening (т.е. когда краткосрочные ставки снижаются сильнее, чем долгосрочные) 3) спред “баттерфляй” Факторными дюрациями выступят чувствительности стоимости портфеля к мгновенным изменениям этих факторов на дату 01.12.2022. При их расчете для различных по составу портфелей используются разные виды спредов. Например, для “буллета” ОФЗ 26212 показательны спред доходности “2 — 5” и спред “баттерфляй” “0.25 — 2 — 5”, тогда как для длинной ОФЗ 26240 применение спреда доходности “5 — 15” будет предпочтительнее. Факторные дюрации, например, для «буллетного» портфеля равны: D₁ = 3.98, D₂ = — 1.05 и D₃ = 0.79. Значение для D₂ получилось отрицательным, так как увеличение спреда доходности в случае bull steepening приводит к повышению стоимости портфеля. Поправки на выпуклость для купонных облигаций — величины второго порядка, поэтому для приближенных вычислений можно воспользоваться выражением для выпуклости бескупонной облигации с погашением через T лет и непрерывным начислением процентов: C = T²= D². Вместо D можно взять модифицированные дюрации купонных облигаций, а в качестве мгновенного изменения доходности — изменение непрерывной спотовой ставки Δsₙ₋₁ для срока до погашения равного дюрации купонной облигации на 01.12.2022. Корректно рассчитанная выпуклость купонной облигации будет больше, чем у бескупонной той же дюрации, но это различие не столь критично для примерных расчётов. Также необходимо учесть форвардную поправку fₙ₋₁,ₙ, поскольку все факторные дюрации и выпуклости рассчитаны не на момент приобретения портфеля 01.06.2022, а на горизонте инвестирования 01.12.2022, т.е. спустя полгода и в предположении неизменной КБД.
Собирая все вместе, получим прогнозное значение доходности портфеля за полугодие:
HPR ≈ текущая доходность + roll down + (1+fₙ₋₁,ₙ)⋅( —D₁⋅Δx₁ —D₂⋅Δx₂ —D₃⋅Δx₃ + 0.5∙Cₙ₋₁∙(Δsₙ₋₁)²)
Например, для “буллета” ОФЗ 26212 HPR ≈ 7.75% + 1.51% + 12% = 21.26% годовых, что выше, чем прогнозный HPR “барбелла” — 14.11% годовых. Это связано, в основном, с тем, что согласно прогнозу инвестора ставки для небольших сроков до погашения должны снизиться сильнее, чем долгосрочные, поэтому изменение формы КБД оказало бы наибольшее влияние на доход по облигациям с дюрацией менее 5-ти лет.
Проведя это небольшое исследование, инвестор останавливает свой выбор на “буллетной” структуре портфеля и вкладывает все средства в ОФЗ 26212.
Внимательный читатель сразу заметит, что все вычисления в пунктах 1., 2. и 3. легко заменить одной точной формулой: HPR = 2⋅(P₀₁.₁₂ — P₀₁.₀₆ + Coupon)/P₀₁.₀₆ (в годовом выражении) Ведь у нас уже есть прогнозная КБД на 01.12.2022 и мы можем ее использовать для получения новых цен облигаций. HPR “буллета”, рассчитанный точными методами, равен 7.75% + 2⋅(971.02-910)/910 = 7.75% + 13.41% = 21.16% годовых. Для “барбелла” аналогичная доходность составит 7.7% + 2⋅[0.498⋅(1000-984.8)/984.8 + 0.502(889.2-845.3)/845.3] =7.7%+6.75% = 14.45% Возникает вопрос, зачем же мы всё усложняли последовательными приближениями, когда могли гораздо проще получить точный результат? Всё дело в том, что если инвестор использует лишь один-два сценария движения КБД, так и следует поступать, т.е. оценивать стоимость портфеля по точной формуле. Но при расчете ожидаемого HPR для большого по составу портфеля придется рассматривать множество сценариев динамики КБД. Среди них желательно выбрать один базовый, — чаще всего неизменную форму КБД, — и затем назначить всем сценариям определенные вероятности. Такой подход называется сценарным анализом. Проще всего его проводить, заранее и единожды рассчитав rolling yield, факторные дюрации и т.д., задать вероятностное распределение для факторов и найти их ожидаемые величины и дисперсию, например, методами Монте-Карло. Впрочем, ничто не мешает опытному программисту варьировать всю КБД как целое и получать те же оценки удобными ему численными методами.
Однако жизнь изменчива и часто подтверждает известную поговорку о том, что “загад не бывает богат” Реальная КБД на 01.12.2022 оказалась совершенно другой (сплошная тёмно-лиловая линия на рисунке), так как известные события конца сентября 2022 г. оказали существенное влияние на российский фондовый рынок. КБД действительно приняла нормальную форму, но в том числе и за счёт существенного роста долгосрочных ставок. Спред доходности “0.25 — 30”, отражающий большей частью премию за риск, на 1-е декабря достиг практически 400 б.п., что довольно много по историческим меркам и отражает неуверенность участников рынка в будущем.
По счастью, принятое инвестором решение в какой-то степени защитило его средства — “буллетный” портфель пусть и не заработал высокую доходность, но практически ничего не потерял по сравнению с краткосрочным банковским вкладом: HPR в годовом выражении составил 7.75% + 2⋅(924 — 910)/910 = 9.29%, тогда как стратегия “барбелл” показала бы очень скромный результат — годовую доходность в 7.7% — 5.7% = 2%. Как мы обсуждали ранее, это связано с тем, что “барбелл” плохо переносит bear steepening из-за серьезного снижения стоимости долгосрочных облигаций в портфеле.
В нашем примере мы придерживались определенной дюрации и сравнили лишь две альтернативы. По-хорошему, нам стоило бы перебрать все ОФЗ-ПД и их различные комбинации для поиска максимального полугодового HPR при заданном прогнозе. Поиск оптимального портфеля при отсутствии ограничений — задача сложная, особенно, если используется сценарный анализ. Сценарии могут противоречить друг другу и максимизация HPR в таком случае не всегда может быть правильной целью, особенно для избегающего риска инвестора. Какой портфель выбрать, если есть 50% шансов за то, что ставки вырастут на 100 б.п. и 50% — за то, что упадут на такую же величину, причём эта информация пока неизвестна остальным участникам рынка? В риск-нейтральном подходе рекомендуется выбрать портфель с большей выпуклостью, но будет ли это мудрым решением на самом деле? Возможно, стоило бы купить стрэддл на длинные облигации, если бы подобные опционы существовали на Мосбирже.
В прошлом разделе мы исследовали ожидаемый за период доход и отдельные портфельные стратегии, когда горизонт инвестирования составлял не более одного купонного периода. Мы поступили так, чтобы, по возможности, учесть рыночный риск портфеля, исключив из рассмотрения необходимость реинвестирования купонов и сумм от погашения облигаций. Но если владелец бумаг удерживает их достаточно долгое время, ему необходимо принять во внимание оба вида риска. С приближением срока погашения волатильность цен государственных облигаций снижается, их стоимость стремится к номиналу, а значит для инвестора, решившего держать облигации до погашения, рыночный риск не имеет значения. Риск реинвестирования выходит в этом случае на первый план.
Например, для 10-летки с полугодовым купоном 4%, выпущенной за номинал, доля от реинвестирования купонов в общей массе дохода составит почти 1/3, если их все удастся вложить под эту же ставку (800 р. купонами и 391 р. прибыль от реинвестирования) Но если сразу после покупки ее YTM понизится с 8% до 5% и останется таким до срока погашения, эта доля уменьшится до 22%, а потери от уменьшения ставок составят более 40% (222 р. вместо 391 р.) В частном случае плоской и неизменной КБД доход от реинвестирования купонов равен:
C⋅([(1+y)ⁿ -1]/y — n),
где C — величина купона за период (например, полугодие, квартал и т.д.), n — число периодов, y — процентная ставка за период (если указана номинальная доходность к погашению или BEY, то y = BEY/k, где k — число периодов за год)
Чем длиннее облигация, тем больше доля “сложного процента” в планируемом доходе, а значит выше риск реинвестирования. Обычно инвесторы опасаются неожиданного роста ставок, но в случае удержания облигации до погашения он, наоборот, оказывает положительный эффект на накапливаемую прибыль: держатель в любом случае получает номинал, а также вкладывает купоны под более высокий процент.
Конечно, можно вообще избежать риска реинвестирования, купив длинные бескупонные облигации, для которых HPR на дату погашения точно известен заранее. Банк России и Минфин РФ уже прорабатывают возможность выпуска таких ОФЗ для населения. Инвестор вправе задаться вопросом, почему тогда на нашем рынке преобладают купонные облигации, ведь промежуточные платежи добавляют немало сложности в расчет ожидаемого дохода? Дело в том, что бескупонная облигация — более рискованный долговой инструмент. Волатильность цен длинных бескупонных облигаций выше, чем купонных той же срочности. На рис. ниже хорошо видно, что модифицированная дюрация бескупонной облигации линейно растёт в зависимости от срока до погашения; в то же время дюрация любой “сверхдлинной” купонной облигации, даже с самым маленьким купоном, будет ограничена D∞ — величиной дюрации консоли (вечной облигации)
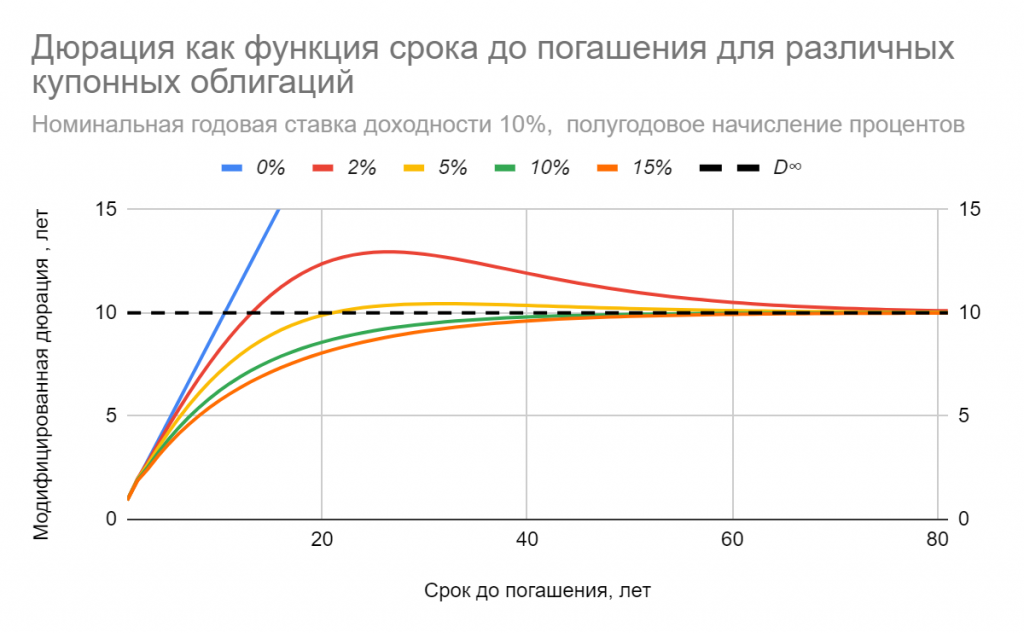
Например, 100 летняя облигация с годовым купоном всего 2% и YTM 10% ведет себя почти как десятилетка с точки зрения риска малых изменений доходности. А если доходность не такой уж длинной 5-летней бескупонной облигации, выпущенной под YTM = 7% (с полугодовым начислением процентов) вдруг вырастет до 10%, ее цена упадет почти на четверть.
На рисунке также заметен малоизвестный эффект — дюрация не обязательно монотонно растет со сроком до погашения перед тем как достигнет предельного значения, ее поведение зависит от соотношения купонной доходности и YTM. Дюрация облигаций с низким купоном поначалу увеличивается, а с некоторого момента снижается, приближаясь к асимптоте D∞. Таким образом, длинные облигации с купонной ставкой ниже YTM могут иметь меньший ценовой риск, чем их более короткие аналоги.
В таблице ниже сравнивается влияние отдельных параметров на риски не содержащих встроенные опционы облигаций с фиксированным купоном:
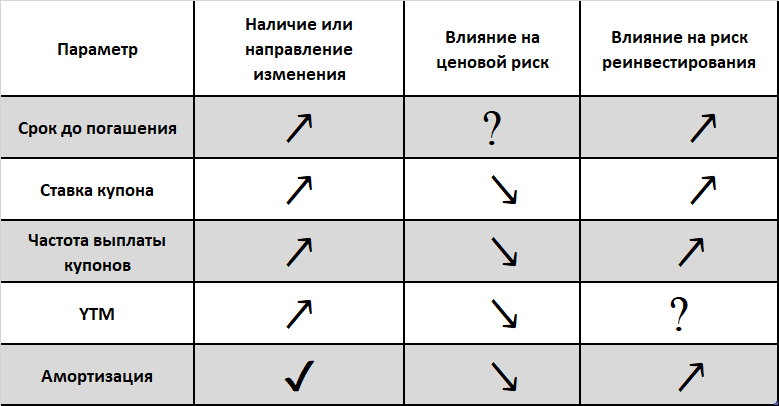
Взаимосвязь некоторых параметров и рисков в таблице не отражена, так как требует дополнительных условий или предположений. Сделаем ряд замечаний:
а) Как обсуждалось выше, не во всех случаях более длинная облигация является и более рискованной.
б) При использовании формулы для дюрации Маколея, например, в табличных процессорах Excel или Google Sheets обнаружится, что увеличение частоты выплаты купона уменьшит ее значение. Но модифицированная дюрация, рассчитанная по этим же правилам, ведёт себя противоположным образом — она растет с увеличением числа купонных платежей в году, т.е. парадоксальным образом выше будет и процентный риск. Вместе с тем, как мы обсуждали в самой первой статье нашего цикла, формальный подход к дроблению денежных потоков вне их связи с доходностью к погашению может приводить к парадоксальным либо неверным результатам (различия между номинальной и эффективной доходностями) Необходимо каждый раз согласовывать периодичность купонных выплат и применяемой процентной ставки. В этом случае правильно рассчитанная модифицированная дюрация всегда уменьшается с увеличением частоты выплаты купонов.
в) С одной стороны можно считать, что риск реинвестирования при росте YTM снижается в силу асимметричности, так как купоны могут вкладываться под более высокую доходность, уменьшая опасность того, что накопленная прибыль будет ниже таргета. Однако если понимать этот риск как меру неопределенности будущего дохода вообще, то он не зависит от направления изменения ставок.
Стратегия долгосрочного инвестора, не собирающегося заниматься реинвестированием купонных выплат, зависит от его целей. Допустим, рассматриваемый им срок вложений составляет 10 лет и он выбирает между альтернативами: приобрести 10-летнюю облигацию с постоянным купоном, например, ОФЗ 26241, либо длинный флоатер — ОФЗ 29017. Если покупатель намерен каждые полгода получать конкретную сумму как прибавку к своей пенсии, рассчитывает только на купоны и не желает трогать капитал вплоть до срока погашения облигации, то ОФЗ с постоянным купоном — его выбор, поскольку все выплаты по ним известны заранее. Флоатер же будет для него более рискованной инвестицией, так как в зависимости от динамики краткосрочных ставок размеры сумм получаемых купонов могут сильно разниться. С другой стороны, флоатеры устойчивы к колебаниям ставок на протяжении всего срока удержания и не склонный к ценовому риску инвестор предпочтет именно их. О том как быть в ситуации, когда хочется тратить и купоны и часть капитала мы поговорим позднее, а пока будем исходить из того, что все купоны реинвестируются.
Вообще говоря, доход на горизонте свыше одного купонного периода FVₙ включает в себя:
ожидаемое изменение величины капитала
все купонные выплаты по облигации (портфелю), а также накопленный купонный доход (разницу между начисленным и уплаченным)
доход от реинвестирования купонов
Доходность приходящаяся на один период (полугодие, квартал, месяц) за время удержания облигации равное n периодам:
HPRₚ= [FVₙ/P]¹/ⁿ — 1, где FVₙ — полученный доход, P — начальная стоимость инвестиции, включающая НКД. Эту доходность можно привести к годовым величинам двумя разными способами:
Номинальный HPR = k⋅HPRₚ, где k — число периодов в году; это расчет на основе BEY (bond equivalent basis)
Эффективный HPR = (1 + HPRₚ)ᵏ — 1, где k — число периодов в году; аналогичен (но не равен) эфф. доходности в Quik и его удобнее использовать для сравнения облигаций с разной частотой купонных выплат.
Неизвестными составляющими для расчёта многопериодного HPR ОФЗ с постоянным купонным доходом являются (1) и (3), а длинных ОФЗ с переменным купоном — (2) и (3) Вследствие этого риск реинвестирования у флоатеров выше, чем у длинных ОФЗ-ПД, и их долгосрочное удержание аналогично роллированию коротких облигаций.
Ожидаемое изменение величины капитала для портфеля ОФЗ-ПД зависит от мнения инвестора о том, как будет выглядеть КБД на момент продажи и насколько сильно она отклонится от текущей формы. Т-летняя облигация по прошествии t < T лет будет иметь такой же ценовой риск, как и вновь выпущенная (T-t)-летняя бумага с аналогичной ставкой купона. Если инвестор в своем прогнозе учитывает только параллельные сдвиги КБД, он может оценить прирост капитала подобно тому, как это было проделано выше для краткосрочного вложения. Он рассчитает roll down, дюрацию D(T-t), рассмотрит различные сценарии и так далее. Но давайте задумаемся, имеет ли смысл приобретать длинную облигацию, допустим, 10-летку при горизонте инвестирования всего в 3 года? Оправдает ли более высокая доходность к погашению (в случае нормальной формы КБД) возможный риск неблагоприятного изменения цены? Из практики следует, что разумному частному инвестору стоит вкладываться в длинные облигации, если он совершенно уверен в том, что цикл повышения ставок уже пройден и на рынке наметился разворот, как это было в 2015-м, 2020-м гг, и, возможно, произошло в начале 2022-го года. В остальных случаях лучше выбрать бумаги со сроком погашения равным или близким к горизонту инвестирования.
Наблюдения показывают, что для “долгосрочного” владения физлица предпочитают бумаги срочностью от двух до пяти лет, что соответствует большинству выпусков корпоративных и муниципальных облигаций. В бумагах, удерживаемых до погашения, составная часть накопленного дохода (1) уже не будет неизвестной (случайной) величиной — в конце срока обращения надежной облигации инвестор заведомо получает номинал. Поэтому нам остается проанализировать только части (2) и (3) этого дохода.
Как мы уже отмечали, долгосрочное удержание ОФЗ-ПК сродни роллированию очень коротких ОФЗ-ПД. Процентный риск у таких бумаг довольно мал: модифицированная дюрация составляет несколько месяцев. Начиная со второго полугодия 2019-го года Минфин выпускает ОФЗ-ПК с плавающей купонной ставкой, привязанной к RUONIA без премии. Купонный доход в таких ОФЗ рассчитывается исходя из среднего значения ставок RUONIA за последние три месяца, которые заканчиваются за семь дней до даты определения ставки купона. Полезный и краткий обзор флоатеров и линкеров проведен, например,в статье брокера “Тинькофф Инвестиции” Единственный спорный тезис в этой статье:
“Купив ОФЗ с фиксированным купоном в 8% и продержав данную бумагу до погашения, вы получите только 8%, даже если ЦБ в один февральский день поднимет ставку до 20%, а инфляция побьет все рекорды. Купив флоатер, вы не пропустите внезапную высокую доходность на рынке”
Очевидно, что удерживаемая до погашения ОФЗ-ПД с купоном 8% может дать доходность как выше, так и ниже 8% — это зависит от цены приобретения и динамики ставок для реинвестирования купонов. Флоатер действительно не даст пропустить “внезапную” высокую доходность, но, во-первых, слегка усреднит ее, а во-вторых, такие доходности не только внезапны, но и достаточно редки и не задерживаются на рынке дольше, чем того требуют приличия. Большую часть времени ОФЗ-ПК выплачивают весьма умеренный доход, достаточно вспомнить скромные 4%-4.5% в 2021 г.
“Новые” флоатеры достаточно точно отражают текущий уровень краткосрочных процентных ставок, поэтому их цена держится у номинала. Допустим, что все полученные купоны вкладываются в ту же облигацию, тогда периодическая (в нашем случае период это квартал) доходность приблизительно будет равна
HPRₚ = [FVₙ/P]¹/ⁿ — 1 ≈ [(1 + r₁)⋅(1 + r₂)… ⋅(1 + rₙ)]¹/ⁿ — 1 ,
где rᵢ — периодические ставки купонов, выплачиваемых по ОФЗ-ПК (если, к примеру, средняя ставка RUONIA за предыдущий квартал составила 8% годовых, то соответствующая ей периодическая ставка r = 8%/4 = 2%)
Значения будущих купонных ставок инвестору неизвестны и ему необходимо составить прогноз (или провести сценарный анализ) для возможных изменений среднего значения ставок RUONIA вплоть до горизонта инвестирования. Можно численно симулировать динамику самой RUONIA, а затем поквартально усреднять результаты. Для упрощения расчетов при сценарном анализе лучше сразу заменить обычные ставки купонов rᵢ логарифмическими yᵢ = ln(1+rᵢ), тогда периодический HPR в непрерывном начислении равен среднему арифметическому ставок yᵢ, т.е. выборочному матожиданию случайной величины Y, принимающей значения Y = yᵢ и описывающей динамику логарифмических купонных ставок. Вероятностный подход в контексте нестационарного процесса с неизвестной плотностью распределения имеет, конечно, свои нюансы, но для практических целей вполне пригоден.
Для прогноза будущих ставок RUONIA инвестор может выбрать метод пристального взгляда на левую часть графика, технический анализ, использование различных моделей (ARIMA, модель возврата к среднему с трендом, стохастические модели динамики краткосрочных ставок и т.д.) Все они имеют равную ценность в условиях текущей высокой неопределенности и ничем не лучше мартингального ожидания — завтра всё будет так же, как и сегодня.
И всё же мы можем попытаться обобщить имеющуюся на данный момент информацию.
Банк России посылает сигналы, что не будет слишком спешить с дальнейшим понижением ключевой ставки, постарается какое-то время сохранить ее примерно на текущем уровне, а при возникновении угрозы роста инфляционных ожиданий допускает краткосрочный цикл повышения ставок. Вместе с тем цель денежно-кредитной политики остается неизменной, — поддержание инфляции вблизи 4% — а значит, по ее достижении ключевая ставка должна быть ниже текущих значений.
В октябре-декабре 2022 г. были размещены ОФЗ-ПК серий 29021, 29023, 29022 общей суммой 2.5 трлн рублей, что составило более 76% от всего объема размещений за год. Доля флоатеров и линкеров в портфеле Минфина составляет уже около 40%. Это много, так как еще в 2017 г. Минфин установил безопасную отметку в 25% объема государственного внутреннего долга, выраженного в ценных бумагах с плавающей ставкой.
В конце 2022 г. на итоговом брифинге с журналистами А. Силуанов заметил:
“Мы ранее говорили, что около трети, до 40% [должна быть доля флоатеров в портфеле]. Сейчас нет такого жесткого таргета, сколько их должно быть — 40%, 35%, 50%. Понятно, что сегодня большие объемы занять можно только по плавающим ставкам, потому что по фиксу такие объемы не взяли бы. Придет время, наоборот, будут пользоваться спросом бумаги с фиксированной доходностью…”
Обратим внимание, как легким движением руки 25% превратились в элегантные “около трети” и “до 40%” и вспомним, что еще два года назад министр финансов сетовал:
“Мы в этом году [2020-м ]заимствовали через бумаги с плавающим купоном в основном, а это выгодно банкам, но не выгодно заемщику, потому что случись что, RUONIA вырастет, мы будем больше платить. Это для нас не очень комфортный инструмент. Стабильные ставки — по ним не хотят много брать, берут иностранцы, как правило, наши хотят плавающую ставку, чтобы себя захеджировать. Нам тоже не хочется зависеть. А то раньше был валютный долг, были зависимы от курса доллара, а теперь у нас долг в зависимости от RUONIA — тоже риски. Это, кстати, серьезная штука”
Иными словами, Минфин с большой неохотой увеличивает долю флоатеров в своем портфеле, но faire bonne mine à mauvais jeu. Банки скупают на аукционах ОФЗ-ПК не из-за уверенности в грядущем повышении ставок, а чтобы хеджироваться от процентного риска. Минфину приходится идти им навстречу и выпускать вместо ОФЗ-ПД флоатеры в больших объемах. Банки могли бы купить и длинные бумаги с фиксированным купоном, но для этого им придется предложить высокую доходность, что окажет давление на дальний конец кривой, да и сам Минфин не готов заимствовать так дорого.
Все перечисленное указывает на то, что в ближайшее время ЦБ будет крайне осторожен как с повышением, так и снижением ключевой ставки. В среднесрочной перспективе финансовые власти ожидают снижения общего уровня ставок, чтобы Минфин мог выйти на рынок с длинными ОФЗ-ПД.
Как можно заметить, периодический HPR для ОФЗ-ПК представляет собой вторичное усреднение ставок RUONIA (сначала арифметическое, затем геометрическое), а это значит, что он должен иметь низкую волатильность. Средняя ставка RUONIA за последние 10 лет оказалась чуть выше 8% годовых. Рассчитанный при погашении эффективный HPR ОФЗ-ПК 24020 составил около 7% годовых, что соответствует среднему геометрическому купонных ставок за время обращения флоатера, но, что любопытнее, примерно равно ставке самого первого выплаченного купона — 6.88% (см. таблицу ниже)
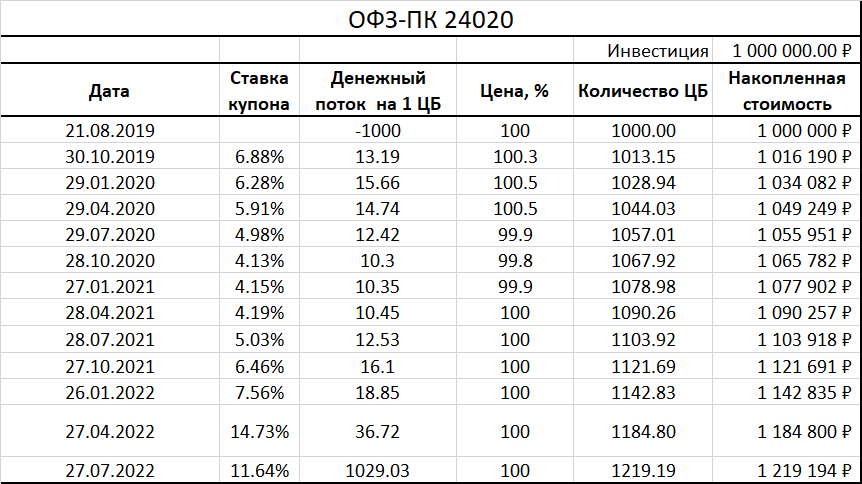
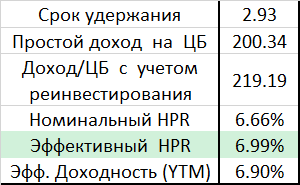
Да, ОФЗ-ПК 24020 удалось “захватить” внезапную высокую доходность первой середины 2022-го года, но для этого пришлось заплатить долгим прозябанием в 2020-2021 гг. Как говорят, то на то и вышло, и именно на схожий сценарий следует ориентироваться частному инвестору, приобретающему сейчас флоатеры на срок два-три года. Наиболее вероятно, что он получит эффективный HPR в пределах 6.5% — 8%
Анализ трёхлетних ОФЗ-ПД, удерживаемых до погашения, немногим сложнее из-за необходимости прогнозировать эволюцию КБД, т.е. инвестору требуется оценить динамику спотовых ставок для сроков погашения менее трех лет. С другой стороны, у таких ОФЗ меньше риск реинвестирования: купонные выплаты известны заранее и ему, по сути, остается рассчитать ожидаемую ставку реинвестирования r.r. (expected reinvestment rate) По аналогии с YTM это предполагаемая единая ставка под которую можно вложить все полученные купоны, и она совпадает с YTM в случае плоской и неизменной кривой доходности. Однако мы знаем, что КБД чаще всего имеет нормальную форму, поэтому в базовом сценарии и при неизменной форме КБД предполагаемая ставка реинвестирования r.r. < YTM для облигаций с фиксированным купонным доходом. Мы уже получали этот результат в одной из прошлых частей для модельных облигаций. Накопленная стоимость двухгодичной инвестиции была меньше рассчитанной с помощью YTM. Это связано с тем, что по мере приближения срока погашения облигации купоны реинвестируются под более низкие ставки, если КБД имеет нормальную форму (и общий уровень ставок в среднем не растёт) Поэтому, чем больше срок погашения облигации, тем более консервативную оценку по ставке реинвестирования должен давать инвестор.
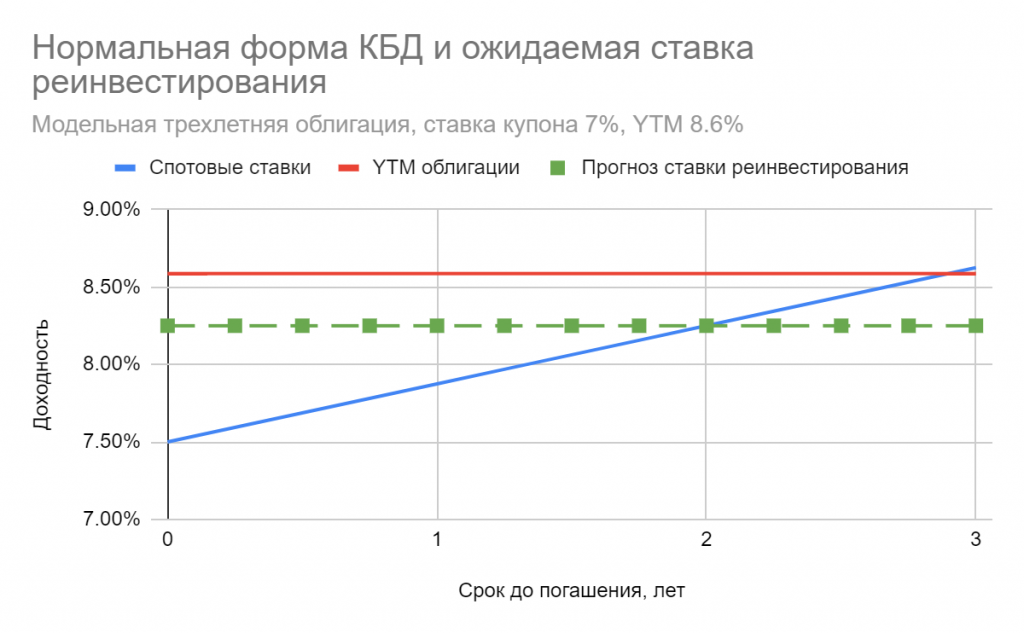
При прогнозировании r.r. инвестор может использовать сценарный анализ, но для 2-х — 3-х летних облигаций достаточно его разумного (и осторожного) суждения, т.к. отклонения от эффективной доходности (указанной в Quik или на сайте Мосбиржи) будут не слишком велики даже при существенных сдвигах КБД в течении срока удержания позиции. Реинвестирование по своей сути это начисление процента на процент и расхождения r.r. от YTM приобретают серьезное влияние на общий доход только на длинном горизонте.
Подводя промежуточный итог, сравним “показатели работы” двух трехлеток, ОФЗ-ПК 24020 и ОФЗ-ПД 26209, приобретенных летом 2019-го года и вместе прошедших тернистый путь до погашения в 2022-м г. Характеристики 24020 были указаны в табл. выше. Ниже они приведены для 26209:
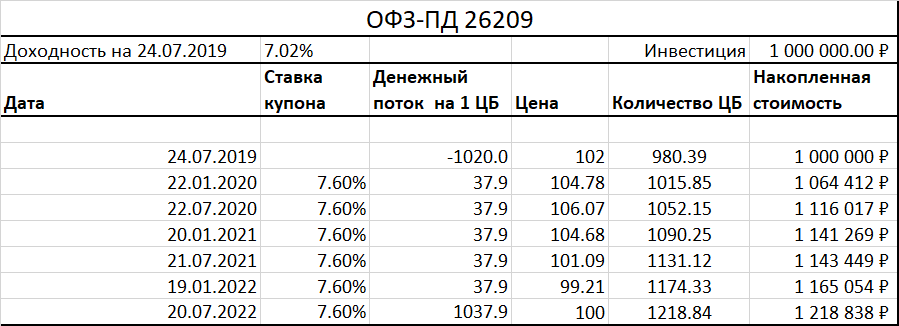
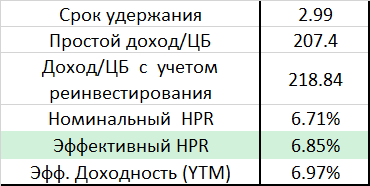
Расчет накопленной стоимости был основан на предположении, что полученные купоны вкладываются в те же бумаги по ценам закрытия рынка на дату выплаты (понятно, что в реальности купоны перечисляются с задержкой, так как жадные брокеры предусмотрительно прописали такую возможность в своих договорах) Изначально инвестируется по 1 млн руб. в каждую облигацию. Учет накоплений удобно вести в количестве облигаций, тогда Xᵢ = Xᵢ₋₁⋅(Couponᵢ /Pᵢ + 1), где Xᵢ — количество облигаций на дату выплаты купона i, Xᵢ₋₁ — на предыдущую дату, Pᵢ — цена облигации. Стоимость позиции будет равна Xᵢ⋅Pᵢ, все вычисления приведены в приложенном файле Excel.
Видно, что флоатер показал лучший результат несмотря на то, что удерживался меньше почти на месяц. Поскольку большую часть времени купоны ОФЗ-ПД реинвестировались под ставки ниже YTM, ее эффективный HPR оказался меньше, чем эффективная доходность (YTM) Впрочем, эти различия не столь велики.
Флоатеру удалось немного переиграть ОФЗ-ПД в силу двух причин:
В целом середина 2019 г. характеризовалась стабильностью короткого конца КБД, а краткосрочные ставки были очень близки к трехлетним. Это заметно и при сравнении ставки 1-го выплаченного купона по ОФЗ-ПК — 6.88% против YTM ОФЗ-ПД — 7%. Таким образом, у ОФЗ-ПД изначально не было преимущества, т.е. премии за срок.
Последние выплаты по ОФЗ-ПК 24020 полностью нивелировали низкую доходность 2020-2021 гг из-за резкого роста RUONIA в первой половине 2022-г.
Однако подобная ситуация нетипична и трехлетние ОФЗ-ПД, приобретенные на пике ставок 2022 г. и удерживаемые в условиях нисходящей тенденции, скорее всего покажут более высокий эффективный HPR, чем флоатеры с тем же сроком до погашения.

Инвесторы могут приобретать облигации в качестве альтернативы вкладу в банке, ради извлечения спекулятивного дохода или чтобы припарковать временно свободные средства. А иногда им требуется определенная сумма для выплаты долга или необходимо произвести ряд платежей в погашение ипотеки.
Методы подбора облигационных портфелей таким образом, чтобы обеспечить на заданном горизонте доходность не меньше целевой, носят общее название стратегий иммунизации. Целевая доходность рассчитывается для сценария неизменных форвардных ставок.
В случае плоской КБД форвардные и спотовые ставки равны единой и постоянной во времени (эффективной) ставке дисконтирования r(t) = const. Как обсуждалось в прошлых частях, при этих условиях мы можем гарантировать исполнение номинального обязательства L (liability) через T лет, если приобретем портфель облигаций A (assets), стоимость P0[r] которого будет равна приведенной стоимости PV(L):
P0[r] = PV(A) = PV(L) = L /(1+r)ᵀ
В качестве аналога можно привести депозит с капитализацией процентов — клиент точно знает сколько получит при его закрытии. Но в отличие от депозита, срок погашения для облигаций в портфеле не обязан совпадать с T. Важно, что через это время стоимость портфеля станет равна L, т.е. мы можем его продать, чтобы выплатить долг.
Рассмотрим простой пример, когда в экономике действуют номинальные годовые ставки в 10% с полугодовым начислением процентов, т.е. ставка за период (полугодие) равна 5%. Тогда для получения накопленной стоимости 1 млн руб. через 3 года нам потребуется внести на депозит в банке сумму 1 млн/ (1+(10/2)%)² × ³ = 1 млн/ (1+5%)⁶ = 746215 руб. Или можно сначала рассчитать эффективную годовую ставку r = (1+5%)² -1 = 10.25% и получить ту же сумму: 1 млн/(1+ 10.25%)³ = 746215 руб. Десятилетняя облигация с купоном 7% годовых при номинальной доходности 10% будет стоить на рынке ≈ 813 руб. (для выполнения расчета в Excel все цифры необходимо привести к одному периоду, полугодию — PV(5%,20,35,1000)) Если мы приобретем 746215/813 ≈ 918 таких облигаций, то через три года они дадут накопленную стоимость 1 млн руб., что легко проверить расчетами (определив цену облигаций на горизонте 3 лет и инвестируя ранее полученные купоны в те же облигации)
Когда спотовая кривая не является плоской, неизменность форвардных ставок означает, что ее эволюция соответствует “предсказаниям” теории чистых ожиданий (будущие спотовые ставки равны текущим форвардным)

Как следует из предпосылок этой теории, инвестору должно быть всё равно какую облигацию купить, — годичную, трехлетку или десятилетку, — так как если ожидания рынка, “зашитые” в кривой доходности, оправдаются, то все облигации дадут одинаковый HPR в конце периода. Ситуация останется прежней через год, два и так далее. А значит стоимость портфеля облигаций все время будет равна приведенной стоимости обязательства вплоть до срока его уплаты. Подробное доказательство этого факта можно найти у Ю-Дау Люу в книге “Методы и алгоритмы финансовой математики”
Рассмотрим пример для семейства кривых, указанных на анимированном графике. Будущие спотовые ставки можно найти по формулам из главы 4.2.1, расчёты приведены в приложенном файле Excel. Допустим, мы имеем обязательство L номинальной стоимостью 100 ден. единиц и сроком исполнения через 5 лет. Его приведенная стоимость PV(L) = 100/(1+s₅)⁵ = 100/(1+15.62%)⁵ = 48.41. Десятилетняя бескупонная облигация будет торговаться по 100/(1+s₁₀)¹⁰ = 100/(1+17.64%)¹⁰ = 19.7 ден. ед. Если приобрести 48.41/19.7 = 2.46 таких облигаций, то стоимость портфеля A через 5 лет составит (10-летка станет 5-леткой) 2.46∙100/(1+ s*₅)⁵ = 2.46∙100/(1+ 19.7%)⁵ = 100 ден. ед, что в точности покрывает обязательство L. Будущая 5-летняя спотовая ставка s*₅ получена в предположении, что эволюция КБД следует теории чистых ожиданий.
Таким образом, если динамика будущих ставок жестко детерминирована, для достижения цели инвестору достаточно выполнить условие PV(L) = PV(A) в момент покупки облигационного портфеля A.
Во всех остальных случаях невозможно точно рассчитать будущую стоимость процентных бумаг на любой наперед заданный момент времени. Основными драйверами неопределенности выступают ценовой риск и риск реинвестирования, и с ними надо как-то бороться.
Иммунизация единичного обязательства. Плоская КБД.
Когда в одной из прошлых частей цикла мы рассматривали однократные сдвиги плоской кривой доходности, то выяснили, что покупатель, заинтересованный в получении целевой накопленной стоимости, выбирает портфель с дюрацией Маколея равной его горизонту инвестирования. Обсудим этот вопрос немного подробнее.
В финансовой литературе и на популярных сайтах часто можно встретить интерпретации дюрации Маколея как некоего “центра тяжести”:
“Наиболее простое объяснение сути дюрации — это представление финансовых потоков как грузиков, расположенных вдоль стержня (временной оси), находящегося в равновесии на одной точке опоры. Длина стержня — срок до погашения. Дюрация — длина участка от левого края стержня до точки опоры. Расстояние между грузиками — купонный период”
“Дюрация — это точка опоры, уравновешивающая все дисконтированные платежи по облигации”
Эти дисконтированные платежи схематично указаны столбиками в примере на рисунке ниже; “вес” каждого последующего купона уменьшается, последняя выплата включает номинал облигации.
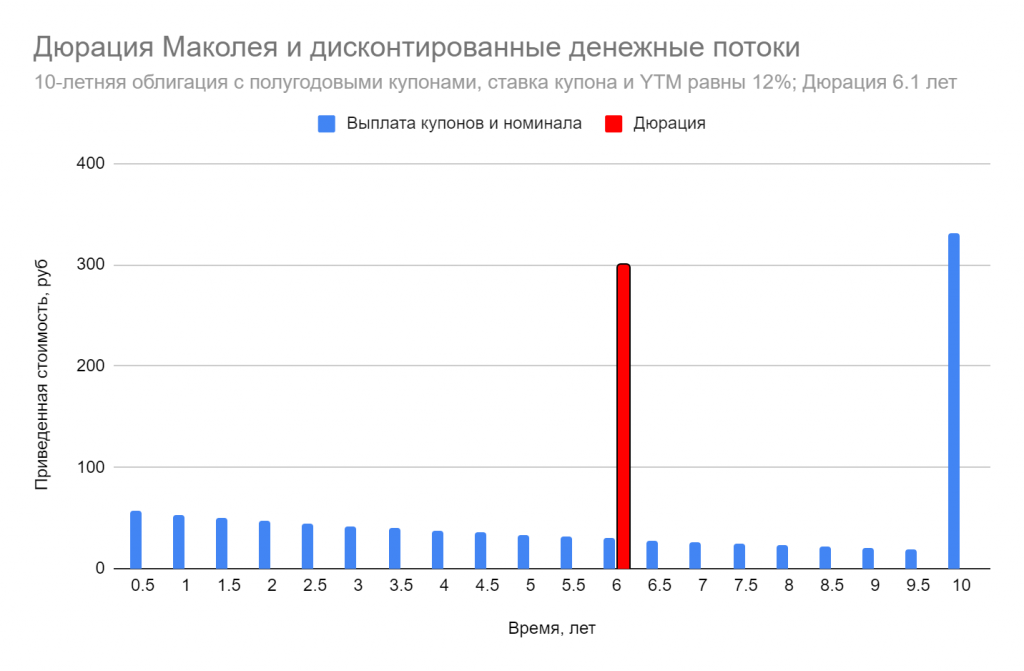
Действительно, если мы изготовим гирьки с весами, равными приведенным стоимостям денежных потоков, и поместим их на линейку в соответствующем порядке, то центр масс всей системы окажется как раз в “точке дюрации” Это следует из его определения как оно вводится в любом школьном учебнике по физике.
Точка на оси абсцисс, соответствующая центру масс невесомого продольного стержня с грузиками:
x꜀ = Σ mₖ·xₖ/M, где mₖ — массы грузиков, xₖ — их координаты, М = Σ mₖ — общая масса системы. В определении дюрации Маколея весам соответствуют приведенные стоимости денежных потоков Cₖ — PV(Cₖ), координатам — сроки до погашения Tₖ, общей массе — стоимость портфеля облигаций.
Поможет ли формальный перенос понятий из курса механики лучше представить, для чего именно нужна дюрация Маколея? Рассчитав центр тяжести, мы знаем как обустроить скамейку или обеспечить поступательное движение тела. Но в случае облигаций нам потребуется уже другая трактовка и про грузики-купоны лучше окончательно забыть. Гораздо удобнее считать, что на горизонте равном дюрации Маколея в равновесии находятся не дисконтированные платежи, а риски портфеля: ценовой и реинвестирования, точнее, их совместное влияние на накопленный доход. Мы предполагаем, что эти риски могут реализоваться в любой момент после приобретения облигации. Когда мы находимся в начале пути и определяем свой горизонт (т.е. анализируем, что будет, если продать бумаги через полгода, год, пять лет), то чем меньше предполагаемый срок удержания, тем выше риск изменения цены. Он исчезает на горизонте совпадающим с датой погашения облигации. И на этом же горизонте максимальным становится риск реинвестирования, который не имеет значения при краткосрочных вложениях.
Дюрация Маколея дает нам точку безразличия в результате однократного сдвига плоской кривой доходности. Она равна количеству времени, необходимому, чтобы первоначальные изменения как цены, так и ставки реинвестирования полностью компенсировали друг друга.
На рисунках ниже приведены примеры портфелей, иммунизированных для достижения целевой накопленной стоимости ≈ 148 ден. единиц на горизонте 4-х лет: пятилетняя облигация номиналом 100 ден. ед. и ставкой купона около 11% (точное значение 10.96%) годовых, и “барбелл” из двух бескупонных облигаций — со сроками погашения 2 и 6 лет. Двухлетка роллируется через каждые два года. Номинальная доходность к погашению (YTM) в момент покупки портфелей составляет 10% годовых, сразу после этого она может измениться на ±50 б.п. Бумаги взяты в “количествах”, обеспечивающих начальную стоимость в 100 ден. единиц для каждого портфеля, что совпадает с приведенной стоимостью обязательства — 147.75/(1+5%)⁸ = 100. Например, пятилетних облигаций всего имеется 0.964 штук. Понятно, что дробных облигаций не бывает, но это просто вопрос масштабирования относительно размера вложенных средств, т.е. на миллион необходимо приобрести 9640 таких бумаг. Дюрации Маколея обязательства и обоих портфелей равны 4 годам.
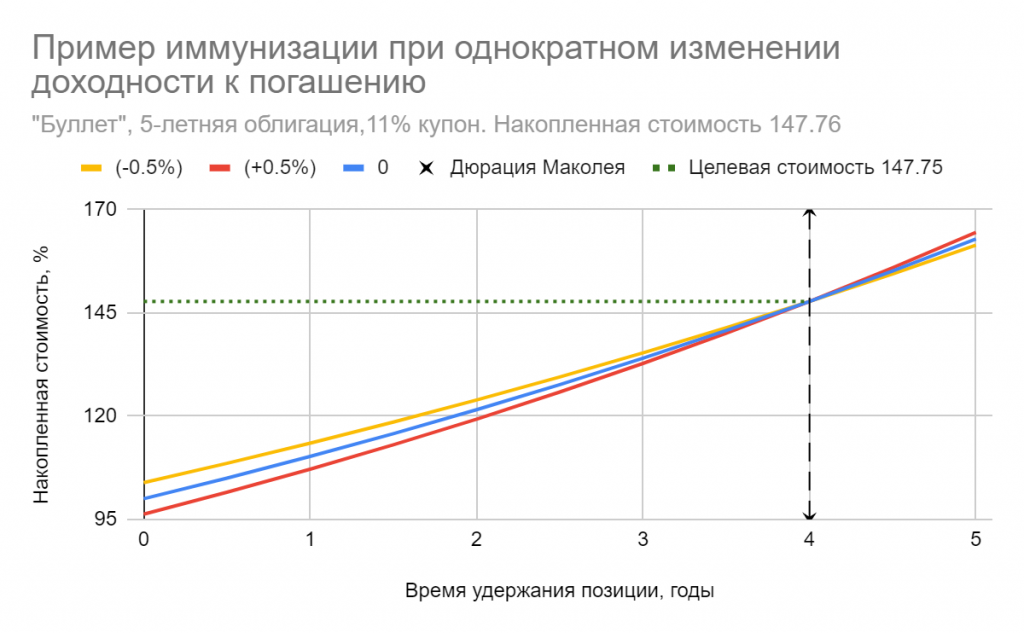
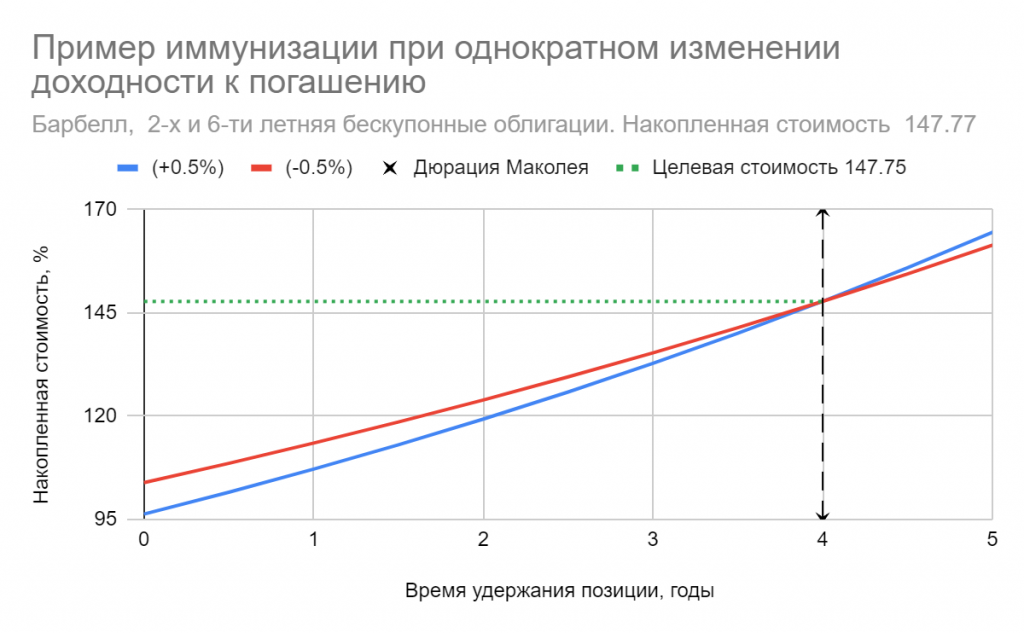
Видно, что если сдвиг кривой доходности происходит единожды, реализованная накопленная стоимость не меньше планируемой. Выбрав любой портфель A с приведенной стоимостью PV(A) = PV(L) и дюрацией Маколея D(A) = D(L) = T (срок погашения обязательства, горизонт инвестирования), инвестор достигнет поставленной цели. При прочих равных лучше сработает иммунизированный портфель, имеющий большую выпуклость. В нашем примере это “барбелл”, и его накопленная стоимость после единичных сдвигов КБД чуть выше, чем у “буллета”. В литературе зачастую приравнивают не дюрации Маколея, а модифицированные дюрации DM =D/(1+rₚ), где rₚ — периодическая доходность к погашению. Для случая плоской КБД разницы в выборе нет, так как доходности yₚ как портфеля, так и обязательства будут все время равны. Однако целевая стоимость достигается именно на горизонте, совпадающим с дюрацией Маколея.
В реальной жизни ставки имеют свойство постоянно изменяться с течением времени. Посмотрим как поведут себя оба портфеля в случае различной динамики плоской КБД, если мы не будем менять их структуру на протяжении удержания позиции (выплаты по купонной облигации вкладываются в ту же бумагу, короткая бескупонная облигация роллируется)
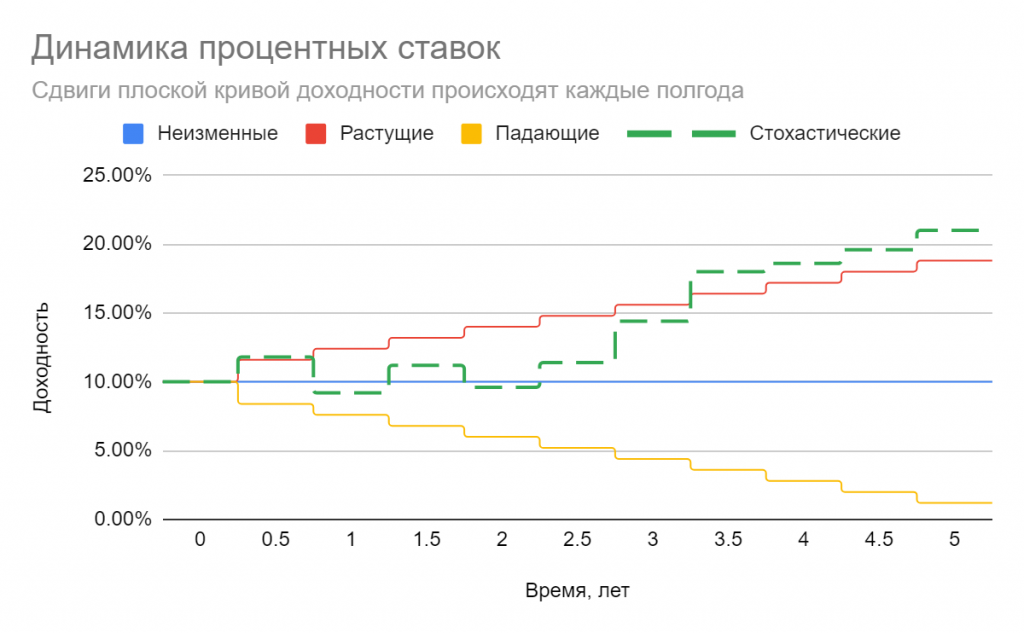
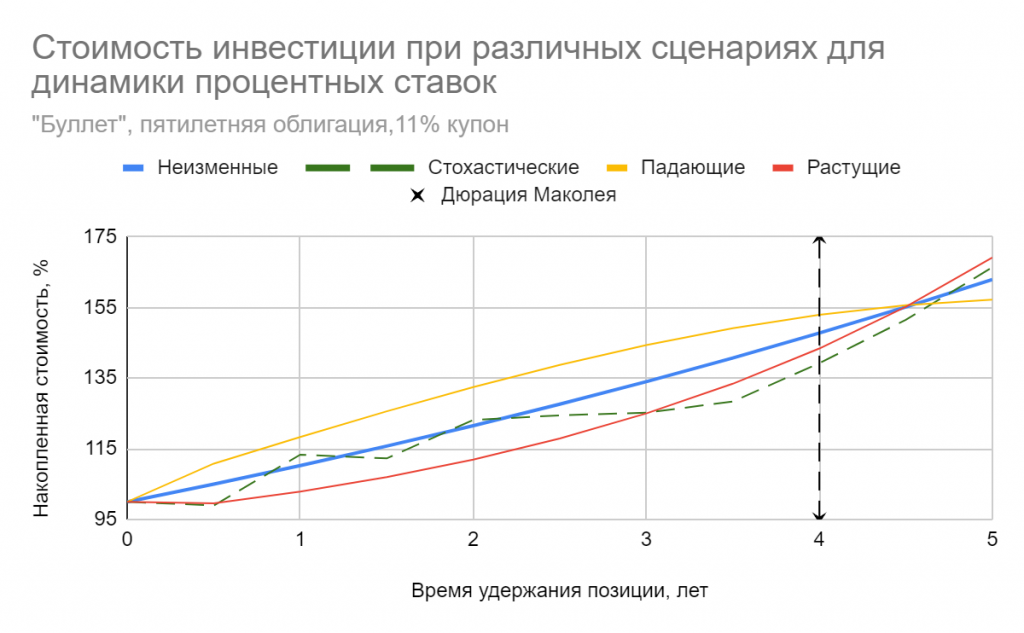
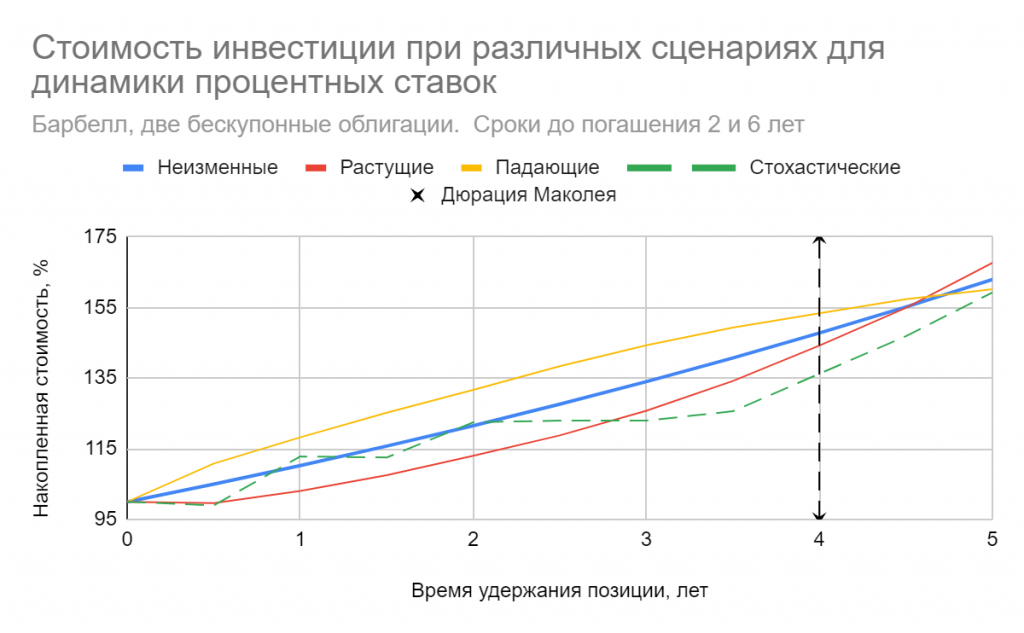
Можно заметить следующее:
1) Во всех случаях многократного изменения ставок накопленная стоимость на горизонте 4-х лет будет различна и не равна целевой сумме, т.е. ≈ 148 ден. единиц.
2) На этом же горизонте у “барбелла” разброс в значениях накопленной стоимости может быть сильнее, чем у “буллетного” портфеля.
3) Реализованная накопленная стоимость будет меньше целевой в случае растущих ставок, и наоборот — больше целевой, если ставки имеют тенденцию к снижению.
Первое наблюдение объясняется тем, что с течением времени дюрации иммунизированного портфеля A и обязательства L уменьшаются с разной скоростью. Это происходит даже в том случае, если ставки не меняются. Обязательство — это аналог бескупонной облигации, и его дюрация Маколея всегда равна оставшемуся сроку до погашения. Дюрация купонной облигации снижается медленнее, так как у такой бумаги срок погашения больше, чем у бескупонной той же дюрации. На рисунке ниже облигация A и обязательство L поначалу имеют одинаковую дюрацию Маколея, равную 8 годам. График дюрации облигации А имеет пилообразный вид, так как мы учли межкупонный период. С уменьшением срока до погашения расхождение дюраций растёт несмотря на отсутствие изменений в доходности.
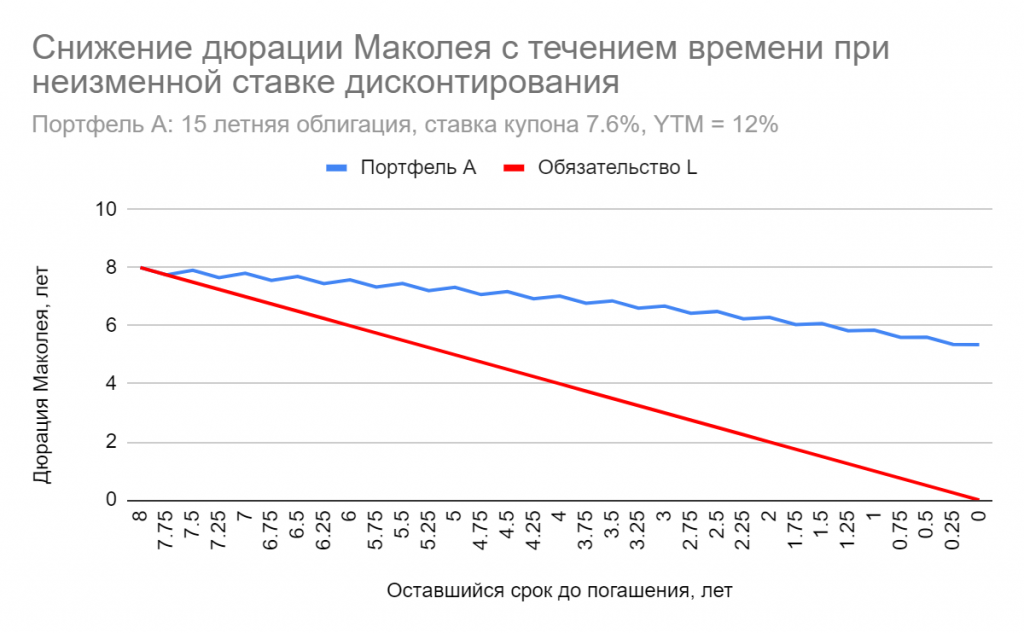
Второй факт связан с тем, что у “барбелла” выше риск реинвестирования. Короткая бумага при роллировании оказывает куда большее влияние на накопленную стоимость по сравнению с относительно небольшими суммами купонов в “буллетном” портфеле. Результат в 3) объясняется превалированием ценового эффекта при длящейся тенденции изменения ставок.
Иммунизация портфеля облигаций — не разовое действие, т.е. она не будет работать сама по себе в рамках парадигмы “купил и держи”. Это требующий корректировок процесс, и портфелю A необходима периодическая ребалансировка даже при неизменных ставках, чтобы обеспечивать равенство D(A) = D(L) Ведь мы не знаем, когда именно произойдет следующий сдвиг КБД и должны быть к нему готовы по мере сил.
На рис. ниже указан пример динамической иммунизации “буллетного” портфеля при стохастических изменениях ставок. Для поддержания равенства дюраций структура портфеля каждые полгода изменяется: часть бумаг продается для приобретения краткосрочных инструментов (например, полугодовых банковских депозитов)
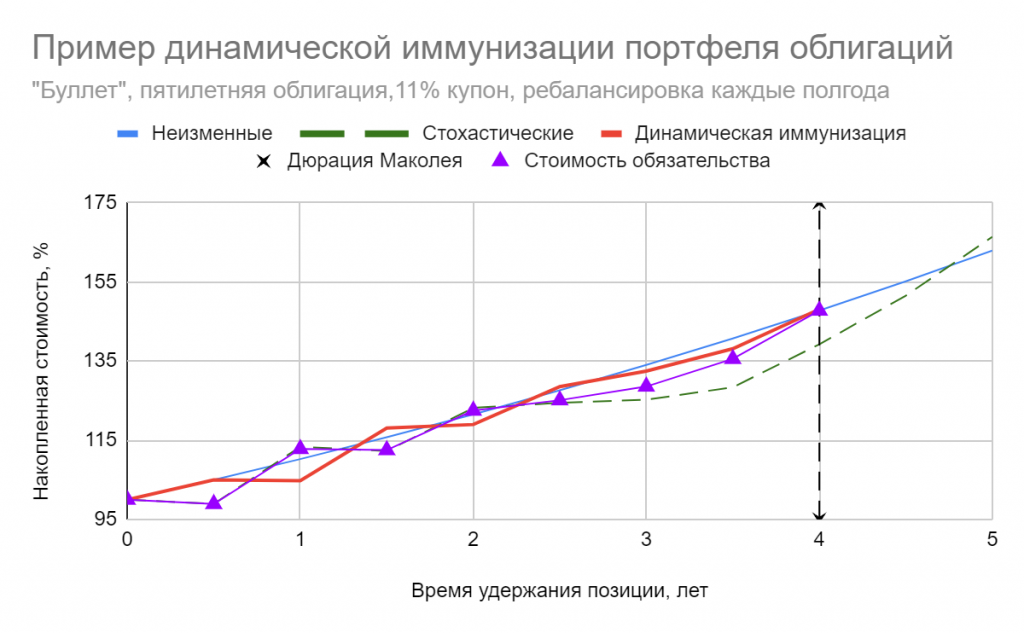
Постепенно все облигации будут “израсходованы” и через четыре года у инвестора на руках окажутся только наличные. Изменения стоимости обязательства L и динамически иммунизированного портфеля A поначалу идут в “противофазе”, но затем колебания сглаживаются. Реализованная накопленная стоимость (148.09) будет чуть выше, чем целевая (147.75), что является заслугой выпуклости, т.к. C(A) > C(L)
В нашем модельном расчете ребалансировка происходит сразу после выплаты купонов и непосредственно перед очередным скачком уровня ставок, поэтому результат выглядит столь впечатляюще. Причем, в этом сеттинге реализованная накопленная стоимость всегда будет больше целевой, независимо от конкретной траектории случайного процесса, описывающего динамику плоской КБД. Ниже представлен результат симуляции Монте-Карло в дискретном аналоге модели CIR с параметром волатильности 2% и возвратом к “средней” полугодовой ставке 5%. Сами расчеты приведены в файле Excel.
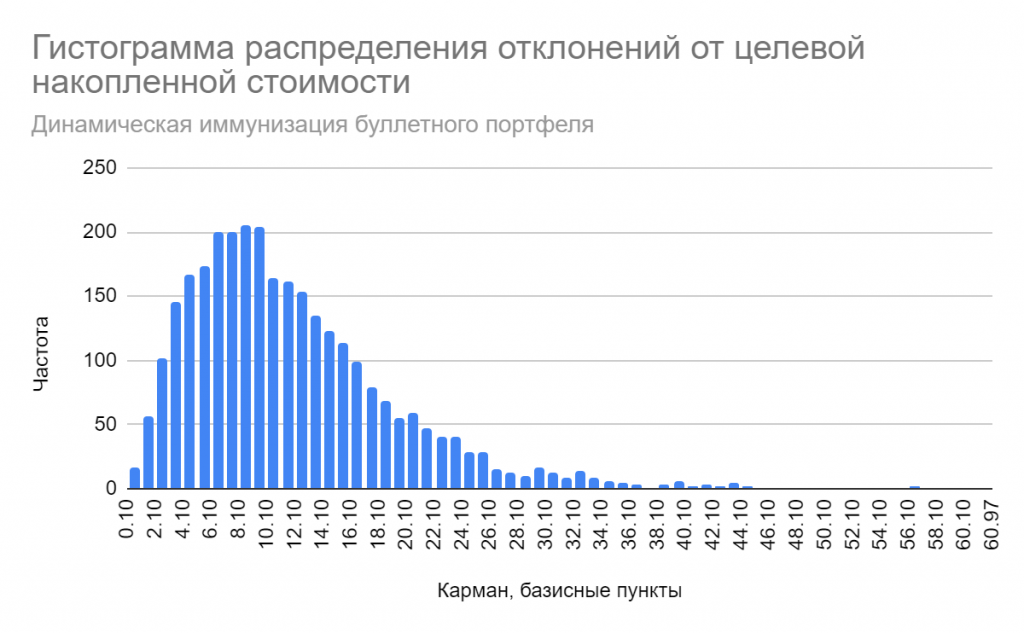
Видно, что распределение относительных смещений от целевой стоимости (RealizedValueₖ — 147.75)/147.75 имеет очень небольшой разброс, а все значения отклонений положительны. Можно сравнить эти данные с вариантом, когда динамическая иммунизация не проводится, т.е. однажды иммунизированный портфель в дальнейшем предоставлен самому себе:
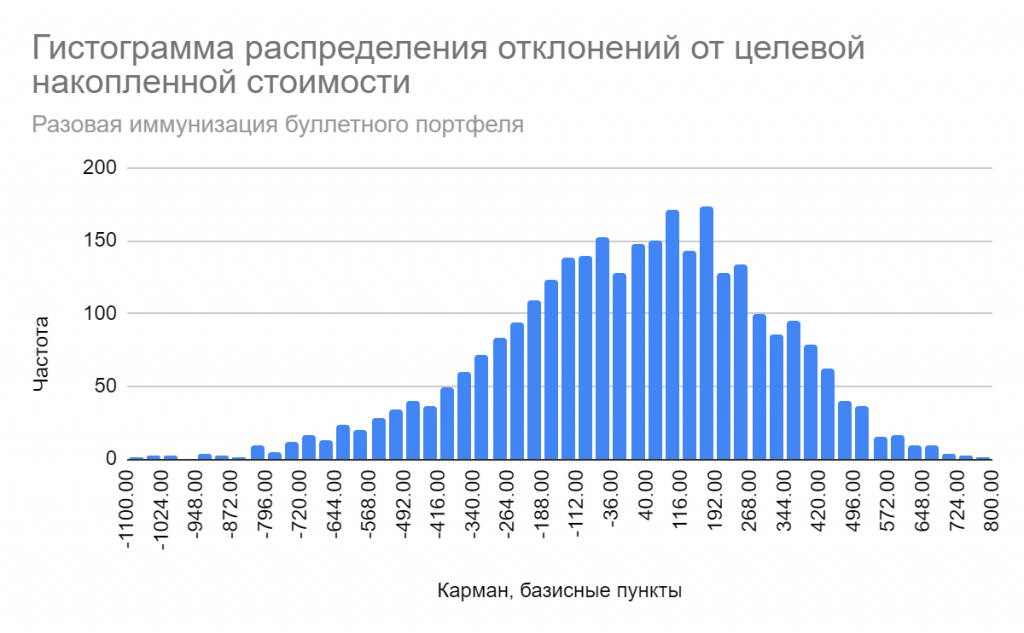
Примерно в половине случаев однократная иммунизация провалится, а для некоторых траекторий ставок “недобор” целевой стоимости на горизонте 4-х лет превысит 10%.
Но, конечно, более корректным будет сравнение результатов динамической иммунизации с колебаниями будущей стоимости облигации, у которой срок погашения равен горизонту инвестора, т.е. в нашем случае 4-м годам:
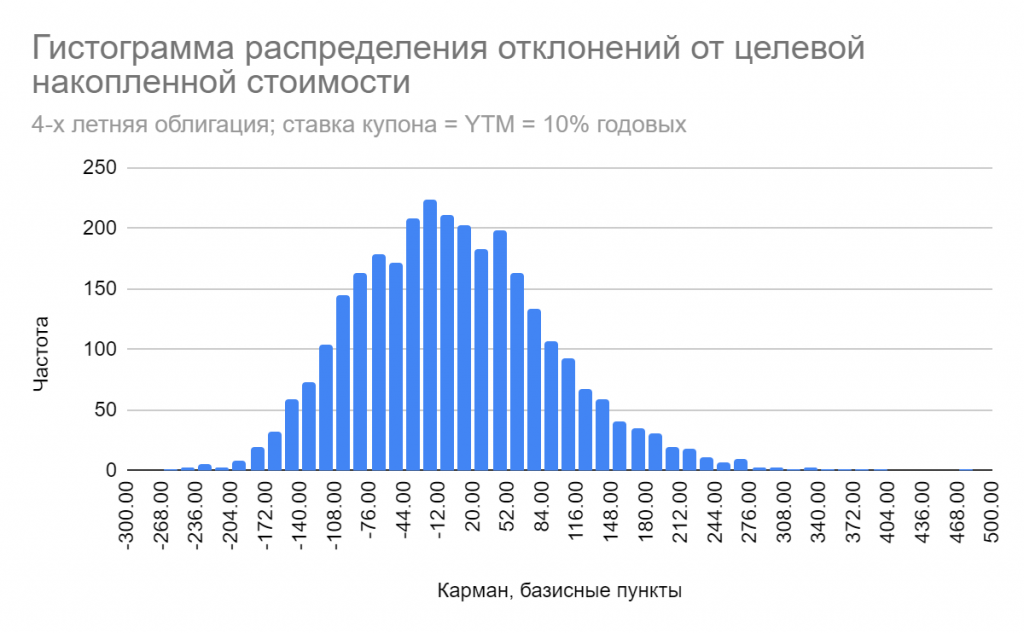
Диапазон отклонений в этом случае гораздо уже, в среднем ± 100 б.п., но все же с вероятностью около 50% инвестор не сможет исполнить обязательство.
Понятно, что в реальной жизни КБД не будет терпеливо ждать, пока инвестор подгонит свой портфель под новое соотношение дюраций. Чем чаще проводится ребалансировка, тем точнее портфель A будет следовать извилистым путям обязательства. С другой стороны, каждое изменение структуры портфеля повлечет за собой дополнительные расходы на уплату комиссионных брокеру и бирже. А значит, необходим какой-то компромисс при выборе частоты ребалансировки. На практике дюрация корректируется сразу после выплаты очередного купона, так как при неизменных или слабо меняющихся ставках портфель остается иммунизированным вплоть до даты следующего платежа (это следствие пилообразного характера дюрации, см. рисунок выше)
Активно управляемый портфель пытается воспроизвести бескупонную облигацию, т.е. стать “зеркальным отражением” обязательства. Знатоки деривативных инструментов, наверное, уже заметили, что динамическая иммунизация напоминает процесс дельта-хеджирования, когда банк хеджирует короткую опционную позицию с помощью базового актива и безрискового долгового инструмента, чтобы создать реплицирующий портфель для проданного опциона. Такая аналогия отчасти справедлива, ведь денежная дюрация (произведение модифицированной дюрации и цены) имеет смысл дельты облигации, а денежная выпуклость — ее гаммы.
Иммунизация единичного обязательства. Произвольная форма КБД
Когда форма кривой доходности отлична от плоской, каждый денежный поток Cₖ дисконтируется по спотовой ставке sₖ, отвечающей периоду его поступления. Портфель A можно иммунизировать, если допустимы только параллельные сдвиги спотовой кривой: ∆sₖ(Tₖ) = ∆s = const. Форвардные кривые в этом случае также изменятся на одну и ту же величину (Redington, Fisher, Weil, Bierwag) Предполагается, что после этого динамика КБД продолжает следовать теории чистых ожиданий, но “отталкиваясь” от новой, смещенной, позиции. По правде говоря, полная защита возможна и в случае, когда ∆sₖ(Tₖ) будет монотонно неубывающей функцией сроков до погашения (это называется выпуклым сдвигом) Но мы не будем усложнять рассмотрение и ограничимся параллельными сдвигами.
Рабочей лошадкой процесса иммунизации будет уже не дюрация Маколея, а просто дюрация, как мера процентного риска, т.е. чувствительность стоимости портфеля к малому параллельному сдвигу КБД, определенная нами в предыдущей главе.
Для m-периодного начисления процентов она называется квазимодифицированной дюрацией:
DQ = (1/P₀)∙Σ (Tₖ/m)∙PV(Cₖ)∙[1 + sₖ/m]⁻¹ (суммирование идет по k)
где приведенные стоимости денежных потоков Cₖ равны
PV(Cₖ) = Cₖ∙[1 + sₖ/m]⁻ᵏ,
P₀ = ΣPV(Cₖ) — стоимость портфеля, Tₖ — время поступления денежных потоков (включая номинал)
Для непрерывного начисления процентов используется дюрация Фишера-Вейля
DF = (1/P₀)∙Σ Tₖ∙PV(Cₖ),
где приведенные стоимости денежных потоков Cₖ рассчитываются при помощи логарифмических спотовых ставок yₖ = ln(1+sₖ),
PV(Cₖ) = Cₖ∙exp(—yₖ∙Tₖ)
Если сдвиг КБД происходит однократно, а в дальнейшем ее динамика определяется форвардными ставками, для обеспечения иммунизации достаточно приравнять приведенные стоимости и денежные дюрации портфеля A и обязательства L. Денежная дюрация облигации равна произведению ее цены и дюрации. Денежная дюрация портфеля равна сумме денежных дюраций составляющих его активов. Иногда вместо денежной дюрации используют аналогичную величину — цену базисного пункта (price value of a basis point, PVBP, DV01) Она меньше денежной дюрации в 10 000 раз.
Обратимся еще раз к примеру спотовой кривой нормальной формы из анимированного графика в начале статьи. Мы уже отмечали, что целевая доходность — это доходность на заданном горизонте любого по составу портфеля в сценарии неизменных форвардных ставок (согласно теории ожиданий все облигации получают одинаковый периодический доход) Ее легче всего рассчитать для бескупонной облигации: целевая доходность на горизонте пяти лет равна спотовой ставке s₅, по которой дисконтируется обязательство L, т.е. 15.62% годовых.
Допустим, мы хотим составить иммунизированный портфель A из двух бескупонных облигаций B₁ и B₂ номиналом по 100 ден. ед. каждая и сроками до погашения 1 год и 10 лет. Необходимые количества бумаг n₁ и n₂ можно найти из системы уравнений:
P₁∙n₁ +P₂∙n₂ = PV(L) (равенство PV(..))
P₁∙n₁∙DQ₁ +P₂∙n₂∙DQ₂ = PV(L)∙DQ(L), (равенство денежных дюраций)
где P₁ = 90.93, P₂ = 19.70, DQ₁ = 0.91, DQ₂ = 8.50 — цены и квазимодифицированные дюрации облигаций в портфеле на дату приобретения; PV(L) = 48.41, DQ(L) = 4.306
Получим: n₁ = 0.294, n₂ = 1.1
Предположим, что сразу после покупки происходит сдвиг спотовой кривой на 50 б.п., а в дальнейшем ее динамика соответствует теории ожиданий вплоть до срока исполнения обязательства. Общая стоимость портфеля FV(A) = 100.03 на горизонте инвестирования складывается из будущей стоимости длинной облигации
FV(B₂) = n₂∙100/(1+ s*₅)⁵ =1.1∙100/(1+20.2%)⁵ = 43.82
и накопленной суммы в результате роллирования короткой облигации
FV(B₁) = P₁∙n₁∙(1+s₁)∙(1+f₁,₂)∙(1+f₂,₃)∙(1+f₃,₄)∙(1+f₄,₅) =
90.93∙0.294∙(1+9.97%)∙(1+14.16%)∙(1+17.08%)∙(1+19.04%)∙(1+20.1%) = 56.2
Будущие однолетние ставки s₁* равны краткосрочным форвардным ставкам fₖ,ₖ₊₁, рассчитанным после сдвига КБД. Подробные вычисления приведены в файле Excel. Стоимость портфеля A через 5 лет покрывает обязательство L = 100 ден. ед. с небольшим запасом, т.к. выпуклость C(A) > C(L).
Понятно, что в реальности КБД не следует теории чистых ожиданий, поэтому состав однажды иммунизированного портфеля необходимо периодически корректировать подобно тому, как это обсуждалось для плоской кривой доходности. В этом случае поддерживается равенство квазимодифицированных дюраций (или дюраций Фишера-Вейля, если используются логарифмические ставки)
Если бы дело ограничивалось лишь параллельными сдвигами КБД, инвестору осталось бы приобрести портфель A с наибольшей выпуклостью, т.е. “барбелл”, выбрать частоту ребалансировки и далее следовать динамической стратегии. На практике возникает так называемый риск иммунизации, связанный с изменениями формы кривой — поворотами и растяжениями. Различные по составу портфели неодинаково реагируют на изменение наклона КБД. Мы помним, например, какую опасность для “барбелла” представляет bear steepening (короткие ставки падают, длинные растут) и такое событие в полной мере отразится на результатах его работы по достижению целевой стоимости. В то же время бескупонная облигация, если ее использовать для покрытия будущего обязательства, от риска изменения формы КБД полностью защищена. Инвестор не может повлиять на динамику кривой доходности, но ему под силу выбрать оптимальную структуру портфеля.
При непараллельных сдвигах кривой доходности мерой риска иммунизации служит статистика M² (Fong, Vasicek)
M² = (1/P₀)∙Σ PV(Cₖ)∙ (Tₖ — H)², где H — горизонт инвестора
Если горизонт инвестора совпадает, например, с дюрацией Фишера-Вейля DF, мера M² равна так называемой дисперсии портфеля S.
S = (1/P₀)∙Σ PV(Cₖ)∙ (Tₖ — DF)²
Дисперсия характеризует “разброс” дат поступлений денежных потоков относительно дюрации портфеля. Дисперсия — малоизвестная величина и ее нет в брокерских приложениях или на сайтах, посвященным облигациям. Она не очень удобна для практических целей, так как дисперсия портфеля не равна средневзвешенной дисперсий составляющих его активов. Дисперсия бескупонной облигации равна нулю, но портфель из бескупонных облигаций имеет, очевидно, ненулевую дисперсию. По счастью, между дисперсией S, дюрацией и выпуклостью C = (1/P₀)∙Σ PV(Cₖ)∙Tₖ² есть простое соотношение.
Для непрерывного начисления:
C = S + DF²; PV(Cₖ) = Cₖ∙exp(—yₖ∙Tₖ), yₖ = ln(1+sₖ), DF — дюрация Фишера-Вейля.
При использовании годового начисления процентов и единой доходности к погашению r:
C = [ S+ D∙(D+1)]/(1+r²); PV(Cₖ) = Cₖ∙[1 + r]⁻ᵏ, D — дюрация Маколея.
Для поиска оптимального иммунизированного портфеля необходимо минимизировать статистику M² при условии DF = H (для простоты взят непрерывный случай) При фиксированной дюрации Фишера-Вейля это означает, что минимальной должна быть выпуклость C, как это видно из соотношений выше. Такими свойствами будет обладать, например, “буллетный” портфель с возможно более низкой ставкой купона и датой погашения наиболее близкой к H, т.е. в идеале портфель по своим характеристикам должен стремиться к бескупонной облигации. Конечно, можно составить произвольный портфель, обеспечив точные равенства D(A) = D(L) и C(A) = C(L), но он будет включать короткие позиции по облигациям, что недоступно большинству инвесторов.
Существуют и более сложные меры риска, связанные с так называемыми моментами D(m) = (1/P₀)∙Σ PV(Cₖ)∙Tₖᵐ, а оптимальный иммунизированный портфель находится методами линейного программирования из системы уравнений D(m) = Hᵐ. Однако для m > 2 этот подход не дает сильного преимущества, опять же в этом случае без коротких позиций не обойтись.
Когда в популярной финансовой литературе обсуждают иммунизацию единичного обязательства, то зачастую пишут про дюрацию Маколея, а не Фишера-Вейля или квазимодифицированную, поэтому сделаем ряд замечаний:
В большинстве ранних работ по теории иммунизации применялось непрерывное начисление процентов, а дюрацией Маколея иногда называли дюрацию Фишера-Вейля, как мы ее определили выше, зависящую от множества спотовых ставок. Для периодического начисления процентов это название также употреблялось, иногда писали про вторую дюрацию Маколея, чтобы как-то различать от основной, которая является функцией единой ставки — YTM.
Использование обычной дюрации Маколея (зависящей от доходности к погашению) исказит правильное соотношение активов в иммунизированном портфеле, но вполне допустимо в качестве приближения. При таком подходе доходность к погашению портфеля нужно рассчитывать как его IRR (внутреннюю ставку доходности), т.е. нельзя брать средневзвешенное значение YTM активов. Это же касается и дюрации Маколея, она должна вычисляться напрямую, а не как средняя дюраций портфеля (хотя редко кто так делает, ведь среднюю гораздо легче считать, а дюрации отдельных облигаций указаны во всех брокерских приложениях)
Проверка на реальных данных показала, что дюрация Фишера-Вейля (или более сложные меры риска) проявляет себя не намного эффективнее дюрации Маколея в процессе динамической иммунизации, т.е. она лучше, но не критично. Возможных причин для этого несколько: во-первых, на длинном участке, имеющем наибольшее значение для результатов иммунизации, КБД имеет почти плоскую форму; во-вторых, с течением времени непараллельные движения частично уравновешивают друг друга, смягчая влияние поворотов на общий накопленный доход; и самое главное — при обсуждении метода главных компонент мы выяснили, что параллельные смещения составляют более 80% всех изменений КБД.
Подведем итог обсуждению иммунизации единичного обязательства. Для обеспечения выполнения обязательства L на горизонте H необходимо построить портфель A, соблюдая условия:
PV(A) = PV(L) (чтобы иметь небольшой запас капитала, можно взять PV(A)≥ PV(L))
D(A) = D(L) (лучше приравнивать денежные дюрации; но если используется дюрация Маколея и единая ставка YTM, то D(A) = H)
C(A)|[D(A)=D(L)] 🠒 min (т.е. при условии равенства дюраций D(A)=D(L) ищется “буллетный ”портфель с минимальной выпуклостью)
D(A) = D(L) (лучше приравнивать денежные дюрации; но если используется дюрация Маколея и единая ставка YTM, то D(A) = H)
C(A)|[D(A)=D(L)] 🠒 min (т.е. при условии равенства дюраций D(A)=D(L) ищется “буллетный ”портфель с минимальной выпуклостью)
Далее проводится периодическая ребалансировка портфеля A. Поскольку риск иммунизации можно минимизировать, но нельзя свести к нулю, достижение целевой доходности не гарантировано, хотя это и происходит в большинстве случаев.
Условная иммунизация
На проблему иммунизации можно взглянуть и с другой стороны. Предположим, что в апреле 2021 г у Елены Николаевны, клиентки Банка “ВТБ”, закончился двухлетний вклад под 7.5% годовых и она решает куда бы пристроить возвращенные на счет 1 000 000 рублей. У нее сберегательная модель поведения и она предпочитает вклады с капитализацией процентов. При этом Елена прекрасно знает про уловки и хитрости банка ВТБ, и понимает, что указанная на сайте доходность — не настоящая, т.е. эффективная, а простая и публикуется специально, чтобы клиенты выбирали капитализацию, а не перечисление на счёт. Эффективную доходность Елена считает сама с помощью функции Excel — EFFECT(x%;12).
Елена стала изучать сайт банка и обнаружила, что текущие ставки по вкладам теперь составляют не более 4-4.5%. Например, вклад, издевательски названный “История успеха”, предлагал всего 4.36% годовых при открытии онлайн. Капитализация могла дать эфф. ставку в 4.45%, что было слабым утешением. Накопленный доход за два года составил бы 1 000 000 ∙(1.0445)² = 1 090 942 руб.
В этом же банке у Елены уже давно был открыт ИИС, но она им пока не пользовалась. Она знает, что раз в год его можно пополнить на сумму 1 млн руб. Быстрый мониторинг ОФЗ в брокерском приложении показал, что доходности двухлеток находятся на уровне 5.8-6% Например, 12 апреля 2021 г. ОФЗ 26215 торговалась с доходностью к погашению около 6% (напомним, что все указанные в Quik доходности — эффективные) Это было больше предлагаемых банком процентов по вкладу, даже с учетом капитализации. Кроме того, оказалось, что длинные облигации дают еще более высокую доходность. Семилетние облигации с YTM в районе 7-7.1% теоретически могли принести доход в 145 000 р. за два года против банковских 91 000 р.
Но Елена Николаевна, конечно, финансово грамотный инвестор и помнит про опасность приобретения длинных облигаций. Она также понимает, что доходность к погашению, указанная в брокерском приложении, может быть полностью реализована лишь в случае удержания бумаг до погашения и реинвестирования всех полученных купонов под ставку YTM. С учетом незначительного риска реинвестирования в коротких облигациях она согласна на эфф. доходность не менее rₘᵢₙ ≈ 5.74% и соответствующую накопленную стоимость в 1 000 000∙(1.0574)² ≈1 118 000 р. на горизонте 2-х лет, но хотела бы попытаться выручить больше, вкладывая в семилетние бумаги, например ОФЗ 26232. Существует ли относительно безопасный план на такой случай?
Елена может попробовать стратегию условной иммунизации. Ее суть в том, что инвестор, рассчитывающий на дополнительный доход, приобретает облигации с дюрацией D > H и YTM > rₘᵢₙ. Далее он следит за стоимостью портфеля, и в случае ее падения ниже минимально допустимой величины, немедленно иммунизирует портфель. Эта минимальная величина будет зависеть от целевой стоимости и уровня ставок по бумагам с дюрацией, примерно равной горизонту инвестирования на момент проверки. Иными словами, в каждый момент времени стоимость позиции Елены должна быть достаточной, чтобы при ее ликвидации она могла приобрести иммунизированный портфель и получить сумму не меньше 1 118 000 р. к середине апреля 2023 г:
Начальные данные:
P(0) = 1 000 000 р., H = 15.04.2023; P(H)⩾ 1 118 000 р.
Условие:
При t > 0 необходимо выполнение неравенства P(t) ⩾ PV(1 118 000), где P(t) — стоимость портфеля в момент времени t, а приведенная стоимость PV(..) рассчитывается либо по спотовой ставке s(H — t), либо через YTM для бумаг с дюрацией примерно равной (H — t)
Нарушение условия в момент t₀:
Немедленная иммунизация, т.е. продажа портфеля и покупка коротких бумаг с дюрацией (H — t₀)
P(0) = 1 000 000 р., H = 15.04.2023; P(H)⩾ 1 118 000 р.
Условие:
При t > 0 необходимо выполнение неравенства P(t) ⩾ PV(1 118 000), где P(t) — стоимость портфеля в момент времени t, а приведенная стоимость PV(..) рассчитывается либо по спотовой ставке s(H — t), либо через YTM для бумаг с дюрацией примерно равной (H — t)
Нарушение условия в момент t₀:
Немедленная иммунизация, т.е. продажа портфеля и покупка коротких бумаг с дюрацией (H — t₀)
Итак, решено: Елена заводит 1 млн р. на ИИС и 14.04.2021 приобретает 1050 штук ОФЗ 26232 по цене 95.25%, сразу после выплаты купона. У нее есть две облигации в качестве кандидатов на “тихую гавань” — ОФЗ 26215 с погашением 16.08.2023 г и ОФЗ 25084 с погашением 04.10.2023. Статистика M² у ОФЗ 26215 равна 0.247 и она меньше, чем у ОФЗ 25084 — 0.294, поэтому Елена берет ее “на карандаш” как будущую основу для иммунизированного портфеля.
Для определения ставок дисконтирования при расчете минимальной PV(..) Елена может использовать либо значения КБД, ежедневно публикуемые на сайте Мосбиржи, либо доходность к погашению ОФЗ 26215, которую можно посмотреть в Quik, на сайте Мосбиржи, или любом брокерском приложении. Например, на дату 30.04.2021 спотовая ставка s = 5.81% для срока до погашения (H — t) = 1.96 года (этот срок считается как YEARFRAC(30.04.2021; 15.04.2023))

Минимально допустимая стоимость портфеля PV(1 118 000) = 1 118 000/(1+5.81%)¹.⁹⁶ = 1 000 851 р.
Какое-то время цена облигации держится на приемлемом уровне, несмотря на продолжающийся цикл повышения ключевой ставки. Поэтому, никаких действий предпринимать не нужно. Опасные моменты возникают в начале июня, в середине июля, и самом начале октября, но Елена каждый раз проверяет условие и не находит повода для беспокойства (см. расчёты в приложенном файле) По счастью, доходности растут не только по длинным, но и по коротким облигациям, что обесценивает минимально допустимый капитал. Кроме того, видно, что выбор ставки дисконтирования не столь важен: стоимости PV(..) мало отличаются друг от друга.
Но вот, 21 октября 2021 рынок закрывается очередной красной свечой и Елена решает больше не рисковать — она продает все свои ОФЗ утром 22 числа по цене 92.65% (включая НКД) и получает 1 005 393 р. Эта сумма больше минимального капитала, равного примерно 1 001 500 р. на дату продажи.
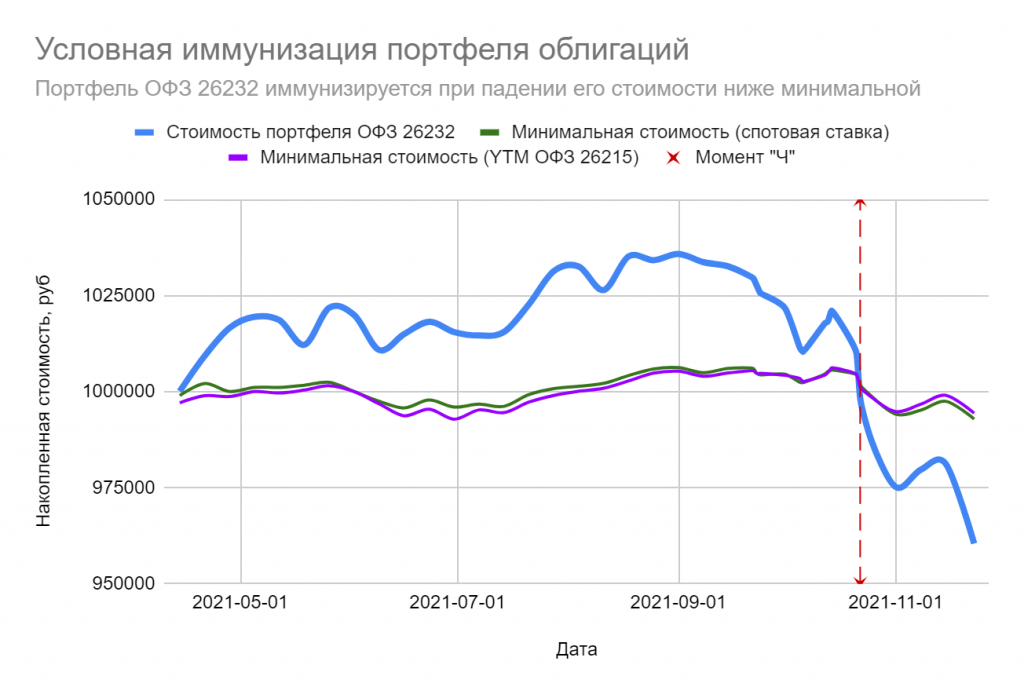
Теперь ей нужно составить иммунизированный портфель. На 22.10.2021 оставшийся до 15.04.2023 г срок равен 1.48 лет, дюрация Маколея ОФЗ 26215, D = 1.715 лет; модифицированная дюрация DM = 1.653 (эти данные доступны на сайте Мосбиржи) Квазимодифицированные и прочие зубодробительные дюрации Елена рассчитывать не стала, так как на коротком горизонте приближений с использованием YTM вполне достаточно.
На самом деле Елена может поступить двояко — или на всю вырученную сумму купить 1000 штук ОФЗ 26215 по цене 100.53% (включая НКД), или разделить деньги между ОФЗ 26215 и ОФЗ 24021, чтобы соблюсти равенство приведенных стоимостей и денежных дюраций. Облигации ОФЗ 24021 — аналог краткосрочного депозита и мы можем считать, что их DM = 0. Добавляя эти бумаги в портфель, инвестор пропорционально уменьшает его дюрацию.
Первый вариант не будет иммунизацией портфеля в строгом смысле, но срок погашения ОФЗ 26215 очень близок горизонту инвестирования Елены. При прогнозе, что цена облигации на 15.04.2023 будет близкой к номиналу, стоимость ее портфеля составит ≈ 1 122 600 р, см. расчет в том же файле Excel. Это больше целевой суммы в 1 118 000 р., но разница объясняется “выгодной” продажей ОФЗ 26232 в октябре 2021 г, когда было сэкономлено как раз около 4 000 р.
Очевидно, что результат динамической иммунизации, если Елена Николаевна возьмется ее проводить, будет ничем не хуже. Мы же не станем ей в этом помогать, ведь она справится и сама.
Не нужно думать, что стратегия условной иммунизации полностью защищает инвестора и одновременно дает ему опцион на дополнительную доходность. В ней много своих подводных камней. Условная иммунизация — аналог постановки заявки “стоп-лосс” в трейдинге и несет схожие риски.
Цены облигаций волатильны в течение дня и не всегда понятно — уже настал момент принять решение иммунизировать портфель, или стоит обождать, понадеяться, что рынок успокоится.
Можно не успеть среагировать, цена длинной облигации способна обрушиться на несколько процентов за считанные часы.
Не всегда есть нужные и достаточно ликвидные облигации для построения иммунизированного портфеля в критический момент. Впрочем, для ОФЗ эта проблема остро не стоит.
Из опыта Елены Николаевны мы можем извлечь важный урок: условной иммунизацией заниматься нет большого смысла, если в экономике наблюдается устойчивая тенденция повышения ставок. Овчинка выделки не стоит. Лучше купить облигации со сроком погашения близким к горизонту инвестора, либо инвестировать в флоатеры и ждать окончания цикла. Гадать, когда наступит “ценовое дно”, не нужно; читать прогнозы аналитиков и напряженно слушать пресс-конференции Председателя ЦБ не нужно; вообще ничего делать не нужно: первое снижение ключевой ставки и будет означать начало разворота, это единственно верный сигнал.
Многопериодная иммунизация портфеля облигаций
Динамическая иммунизация единичного обязательства имеет практический смысл только при большом горизонте инвестирования, т.е. свыше 4-х — 5-ти лет. Частные инвесторы планируют свои вложения, как правило, на срок не более 2-х — 3-х лет. Поэтому, им вряд ли стоит к прибегать к стратегии иммунизации, тем более что ребалансировка требует постоянных жертв в виде уплаты комиссий.
Однако в жизни бывают и другие ситуации. В предыдущем разделе мы отмечали, что не все инвесторы занимаются бесконечным накоплением и реинвестированием, чтобы наблюдать за магией сложного процента. При необходимости получения периодических сумм, когда, например, выходишь “на пенсию в 35” или платишь ипотеку, хорошо бы задуматься о подходящей структуре портфеля облигаций. Можно тратить только купоны, выбрав длинную ОФЗ ПД, но для этого понадобятся крупные сбережения. Во многих случаях без продажи части капитала не обойтись.
Допустим, инвестору нужно произвести серию выплат и ему известны все будущие денежные “оттоки”. Для решения этой задачи он собирается приобрести целевой (dedicated portfolio)портфель, который в конечном счете будет полностью израсходован.
В качестве одного из вариантов он может использовать стратегию полного соответствия денежных потоков. Она строится следующим образом:
Начинаем с последнего по сроку платежа и находим облигации с наиболее близким (меньшим либо равным) сроком до погашения. Они берутся в таком количестве, чтобы их погашаемая стоимость вместе с последней купонной выплатой была равна этому платежу.
Переходим к предпоследнему платежу и поступаем аналогичным образом, плюс учитываем возможные купонные выплаты по облигациям из п.1., попадающие в период между предпоследним и третьим от конца платежом.
Повторяем действия п. 2 …
Продолжаем рекурсию до первого по счету платежа, нанизывая бусины облигаций на временную нить.
Данный подход хорош тем, что позволяет вообще не думать о риске процентных ставок. Но у него есть и серьезные недостатки, самый главный из которых — возможный дефицит подходящих по срокам облигаций. Поскольку для успеха стратегии необходимо, чтобы средства для очередной выплаты в полном объеме поступили заранее, нам придется часть из них какое-то время держать без движения (либо вкладывать под ставки овернайт) Это повышает общие затраты. Если инвестор готов принять дополнительный кредитный риск, он может приобретать корпоративные облигации.
Рассмотрим в качестве примера случай, когда когда на дворе апрель 2023 г и нам нужно произвести следующие платежи в будущем:
01.10.2023 — 200 000 р.,
01.02.2024 — 300 000 р.
01.06.2024 — 500 000 р.
На рынке есть масса подходящих по срокам погашения и относительно надежных облигаций, их достаточно просто отсортировать. Для наших целей подойдут, например, эти:

Для выплаты последних 500 000 р. используем купоны и погашаемую сумму облигаций Сбербанка, их нужно приобрести 500 000/(1000+28.17) = 487 штук (округляем вверх до целой облигации) Для проведения второй выплаты 300 000 р у нас уже есть 487 бумаг Сбербанка, на которые будут получены купоны 28.17∙487 = 13 719 р., поэтому нам останется приобрести (300 000 — 13 719)/(1000 + 43.38) = 275 обл. РЖД. И наконец, для самого первого платежа мы купим (200 000 — 275∙43.38 — 487∙28.17)/(1000 + 37.3) = 169 облигаций ГПБ.

Для трех бумаг все подсчеты легко сделать руками, но в более сложных случаях множественных платежей задачу подбора облигаций лучше решать методами линейной оптимизации.
Менее затратной, достаточно гибкой, хотя и более рискованной альтернативой будет уже знакомая нам стратегия иммунизации. Приемы составления иммунизированного портфеля для исполнения единичного обязательства описаны выше. Так как для каждого отдельного платежа из потока обязательств можно построить свой иммунизированный портфель, то совокупность таких портфелей способна решить общую задачу. Можно показать, что данное условие будет не только достаточным, но и необходимым (Shiu) В предположении выпуклых сдвигов КБД портфель считается иммунизированным в том и только в том случае, если существует его разбиение на компоненты, каждая из которых иммунизирует отдельное обязательство. Одно из следствий этого критерия: дисперсия денежных потоков портфеля должна быть больше либо равна дисперсии платежей по обязательству. Примером такого портфеля будет барбелл, который “охватывает” поток платежей по долгу:
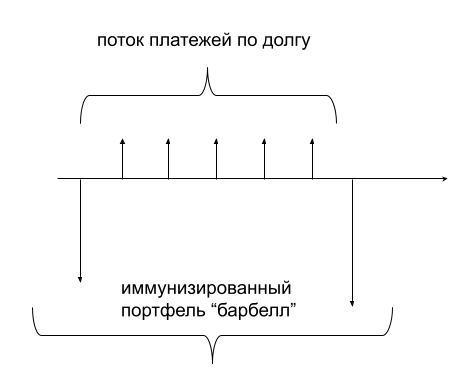
Для наглядности рассмотрим финансирование аннуитета. Покупателю недвижимости необходимо выплачивать ипотеку и для этого он хочет обеспечить поступление на свой счёт одной и той же суммы каждые полгода. Ипотечные платежи, как правило, совершаются ежемесячно, поэтому будем считать, что поступающие средства затем равномерно распределяются по месяцам. Одну часть будущих выплат составят зарплатные доходы, а другую инвестор хочет формировать за счёт созданного целевого портфеля.
Допустим, что инвестор выделил на целевой портфель сумму 10 млн руб., а в экономике действуют номинальные процентные ставки 8% годовых. Выплаты будут осуществляться в течение 15 лет, т. е. 30-ти периодов. Тогда легко рассчитать полугодовой платеж по формуле для аннуитета: ПЛТ(ставка; кпер; пс; [бс]; [тип]) = ПЛТ(4%; 30; —10000000; 0) =578 301 р. При каких предположениях получена эта цифра? Подразумевается, что ставка 8% останется неизменной в течение всех 15-ти лет. Если инвестор внесет 10 млн руб. на 15-летний приходно-расходный вклад с фиксированной ставкой 8% и полугодовой выплатой процентов, будет тратить с него по 578 301 р каждые полгода, то к концу срока вклада он полностью исчерпает средства.
Проблема в том, что банки не предлагают вклады на такой долгий срок, тем более приходно-расходные. Какие есть альтернативы? Можно приобрести 15-летние облигации. Или — открывать краткосрочные вклады. Но как мы уже убедились на примере единичного обязательства, риски изменения процентных ставок приведут к тому, что изначально вложенных средств может не хватить на все запланированные платежи. Особенно неприятной будет ситуация, когда поначалу ставки растут, а потом всё время падают.
Если допустимы только параллельные сдвиги плоской КБД, выход из ситуации прост: приобрести барбелл из 15-летней купонной облигации и краткосрочного инструмента — полугодового вклада.
Для того чтобы найти первоначальное соотношение активов в портфеле A, мы приравниваем дюрации Маколея D(A) = D(L), где D(L) — дюрация аннуитета, и полагаем дюрацию вклада равной нулю:
x∙DM(Bond) + (1-x)∙0 = DM(L)
Получим, что доля облигаций в портфеле на момент его построения должна составлять x = DM(L)/DM(Bond)
В дальнейшем придерживаемся процедуры динамической иммунизации, т.е. поддерживаем равенство дюраций на протяжении всех 15-ти лет, периодически ребалансируя портфель. Все расчеты приведены в файле Excel.
Полученные результаты можно наглядно представить в виде гистограммы распределения конечного баланса инвестора. Видно, что вне зависимости от траектории процентных ставок этот баланс будет всегда положителен при своевременной корректировке иммунизированного портфеля A.

Конечно же, в реальности форма КБД не только не является плоской, но и легко может изменяться в результате наклонов или искривлений, поэтому в случае множественных обязательств также возникает риск иммунизации. А значит, “барбелл” — не всегда удачная идея. Для минимизации риска иммунизации портфель A лучше строить так, чтобы его будущие денежные потоки тесно “охватывали” каждый платеж по обязательству:
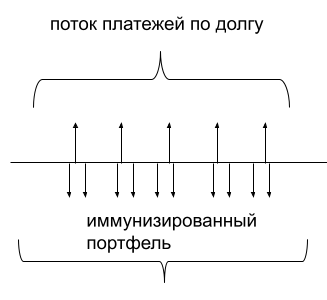
Подводя итог обсуждению многопериодной иммунизации, можно дать следующие рекомендации для составления портфеля A:
MV(A) ≥ PV(L) (MV(A) — рыночная стоимость портфеля, приведенная стоимость потока обязательств PV(L) рассчитывается по текущим спотовым ставкам)
Денежная дюрация портфеля A ≈ Денежная дюрация потока обязательств.
C(A) ≳ C(L) (т.е. выпуклость портфеля совсем немного больше выпуклости потока обязательств)
Денежная дюрация портфеля A ≈ Денежная дюрация потока обязательств.
C(A) ≳ C(L) (т.е. выпуклость портфеля совсем немного больше выпуклости потока обязательств)
У нас остались к рассмотрению небольшие темы, посвященные лестничной стратегии, амортизации, индексным портфелям, линкерам и т.д. Также планировались еще две части: про облигации с встроенными опционами, и заключительная, про корректное сравнение вкладов и облигаций, ради которой, собственно, и затевался весь цикл. Но я принял решение завершить публикации ввиду сложности и неформатности материала, что проявилось в низком интересе читателей. Эта глава будет последней.
Не является индивидуальной инвестиционной рекомендацией | При копировании ссылка обязательна | Нашли ошибку - выделить и нажать Ctrl+Enter | Жалоба

