6 июля 2015 utmedia
Продолжаем тему анализа рынков и портфельного менеджмента. На сей раз рассмотрим тему индексной модели известнейшего американского экономиста Уильяма Шарпа (за что тот, кстати, получил нобелевскую премию по экономике в 1990 году). На сегодняшний день крупнейшие инвестиционные дома и фонды мира, а также международные банки используют именно эту модель для расчета рисков вложений в те или иные активы. Сразу хочется отметить, что теоретическая часть этой модели довольно сложная для освоения, поэтому если будут вопросы, можете задать под статьей либо в рубрике «задай вопрос аналитику».
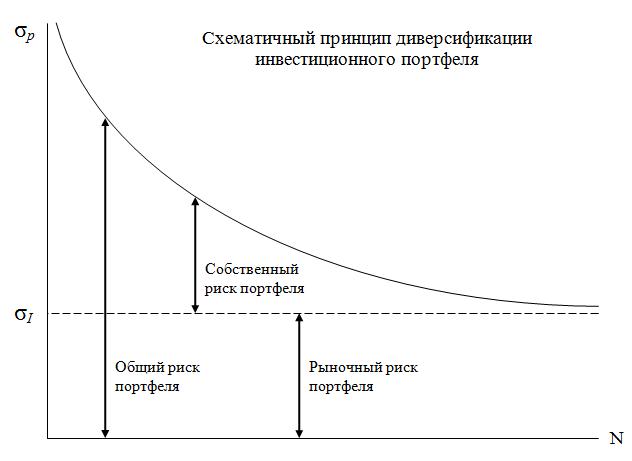
Суть ее заключается в том, чтобы уже имеющиеся методы построения портфелей максимально упростить для снижения трудоемкости процесса (порой для построения портфеля ценных бумаг линейными методами не хватало даже целого штата профессиональных управляющих и финансовых аналитиков). В частности, данная модель использует регрессионный анализ рынка – то есть анализ исторических данных котировок. Понятно, что при ручном регрессионном анализе каждого актива из общей выборки, которая может достигать до нескольких тысяч, потребуется очень значительное время даже при большом штате компетентных сотрудников, поэтому еще в 60-е годы Шарп предложил использовать индексный метод регрессионного анализа для облегчения этого процесса. Сама формула расчета коэффициента Шарпа довольно простая:
S=(Ra-Rf)/sa, где
Ra – доходность непосредственного актива;
Rf – доходность безрисковой инвестиции;
sa – стандартное отклонение актива.
В частности, введено понятие бета-коэффициента, о котором было уже немало рассказано во многих статьях. Формула расчета бета всем хорошо известна: b= Covam/s2m, где Covam – ковариация дохоности актива с рынком, а s2m – дисперсия доходности рынка. Данный показатель указывает на степень риска вложений в тот или иной актив. Долго расписывать тут про это понятие нет смысла, так как цель данной статьи состоит в другом, а более подробно о расчете бета-коэффициента вы можете прочитать в других статьях на моем блоге. Суть модели Шарпа состоит в том, чтобы использовать в качестве бенчмарка уже рассчитанный индекс, исходя из которого и проводился бы расчет риска. Общая же зависимость ценной бумаги от индекса записывается в виде формулы:
ria=aam+bam•rim+eam, где
aam – коэффициент смещения (альфа-коэффициент);
bam – коэффициент наклона (бета-коэффициент);
eam – случайная погрешность;
ria – доходность актива за i период;
rim – доходность рынка за аналогичный период.
Согласно теории Шарпа, бета-коэффициент указывает на зависимость актива от динамики рынка, а в свою очередь альфа-коэффициент – это доходность актива вне зависимости от конъюнктуры рыночного индекса. В случае с бета предполагается, что этот коэффициент статичен от периода к периоду, и поэтому для его расчета достаточно применения метода обычной линейной регрессии. Альфа-коэффициент, в свою очередь, указывает на переоцененность (в случае положительного альфа) или напротив – недооцененность того или иного актива относительно рынка (в случае отрицательного альфа).
Стоит отметить, что как коэффициент альфа, так и коэффициент бета не могут быть абсолютно точными, поскольку это не представляется возможным в силу того, что оба показателя являются динамичными и изменяются в зависимости от котировок цены актива и рынка. Можно лишь дать оценочное значение показателя на основе регрессионного анализа.
Теперь необходимо рассчитать все элементы, данные в формуле. Формула расчета бета-коэффициента приводилась в начале статьи. Альфа-коэффициент определяет доходность актива вне зависимости от динамики рынка. Рассчитывается как разность математического ожиданий доходности рынка в начале периода и доходности рынка в начале периода, помноженная на коэффиицент бета. Формула расчета следующая:
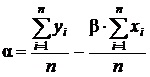 , где
, где
yi, xi – доходность рынка в i период времени.
Последний элемент формулы – случайная погрешность. Этот индикатор указывает на возможную неточность модели Шарпа и является случайной переменной, имеющей нулевое математическое ожидание доходности и стандартное отклонение. Вычисляется по следующей формуле:
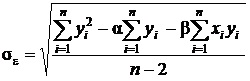
Еще немного стоит уточнить про коэффициент бета. Данный индикатор не может быть абсолютно точным, так как имеет стандартную ошибку – попытку оценить величину таких ошибок:
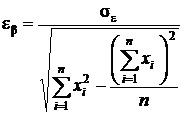
Иными словами, получается как бы замкнутый круг – бета-коэффициент по стандартной формуле пытается рассчитать величину стандартных ошибок, которая изменяется в зависимости от ценовой динамики актива и рынка. Аналогичная стандартная ошибка альфа-коэффициент дает оценку отклонения прогнозируемого значения цены от «истинного»:
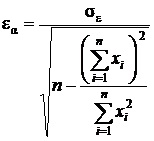
Еще один важный показатель, который часто применяют при расчете характеристик того или иного актива – коэффициент детерминации, или R2, однако об этом будет рассказано в одном из последующих материалов. В западных странах коэффициенты a, b и R2 рассчитываются для всех ценных бумаг регулярно и публикуются вместе с рыночными индексами. Фактически, данные показатели позволяют инвесторам самостоятельно разработать инвестиционный портфель.
Теперь же постараемся обобщить материал непосредственно по модели Уильяма Шарпа. Итак, цель данной модели – упростить линейные методы построения инвестиционных портфелей и регрессионного анализа за счет использования индексов (то есть доходности бенчмарка – фондового индекса либо индивидуально построенного рыночного индекса). Для этого проводится регрессионный анализ – то есть анализируются исторические данные котировок конкретного актива и рынка. При этом ставится задача выявить зависимость изменения цены актива от динамики бенчмарка и исходя из этого рассчитать в конечном итоге коэффициент риска, который станет индикатором актуальности инвестирования в актив. Вот собственно и все. В одном из последующих статей будет выложен конкретный пример расчета коэффициента Шарпа и его использования непосредственно при построении портфеля.

Суть ее заключается в том, чтобы уже имеющиеся методы построения портфелей максимально упростить для снижения трудоемкости процесса (порой для построения портфеля ценных бумаг линейными методами не хватало даже целого штата профессиональных управляющих и финансовых аналитиков). В частности, данная модель использует регрессионный анализ рынка – то есть анализ исторических данных котировок. Понятно, что при ручном регрессионном анализе каждого актива из общей выборки, которая может достигать до нескольких тысяч, потребуется очень значительное время даже при большом штате компетентных сотрудников, поэтому еще в 60-е годы Шарп предложил использовать индексный метод регрессионного анализа для облегчения этого процесса. Сама формула расчета коэффициента Шарпа довольно простая:
S=(Ra-Rf)/sa, где
Ra – доходность непосредственного актива;
Rf – доходность безрисковой инвестиции;
sa – стандартное отклонение актива.
В частности, введено понятие бета-коэффициента, о котором было уже немало рассказано во многих статьях. Формула расчета бета всем хорошо известна: b= Covam/s2m, где Covam – ковариация дохоности актива с рынком, а s2m – дисперсия доходности рынка. Данный показатель указывает на степень риска вложений в тот или иной актив. Долго расписывать тут про это понятие нет смысла, так как цель данной статьи состоит в другом, а более подробно о расчете бета-коэффициента вы можете прочитать в других статьях на моем блоге. Суть модели Шарпа состоит в том, чтобы использовать в качестве бенчмарка уже рассчитанный индекс, исходя из которого и проводился бы расчет риска. Общая же зависимость ценной бумаги от индекса записывается в виде формулы:
ria=aam+bam•rim+eam, где
aam – коэффициент смещения (альфа-коэффициент);
bam – коэффициент наклона (бета-коэффициент);
eam – случайная погрешность;
ria – доходность актива за i период;
rim – доходность рынка за аналогичный период.
Согласно теории Шарпа, бета-коэффициент указывает на зависимость актива от динамики рынка, а в свою очередь альфа-коэффициент – это доходность актива вне зависимости от конъюнктуры рыночного индекса. В случае с бета предполагается, что этот коэффициент статичен от периода к периоду, и поэтому для его расчета достаточно применения метода обычной линейной регрессии. Альфа-коэффициент, в свою очередь, указывает на переоцененность (в случае положительного альфа) или напротив – недооцененность того или иного актива относительно рынка (в случае отрицательного альфа).
Стоит отметить, что как коэффициент альфа, так и коэффициент бета не могут быть абсолютно точными, поскольку это не представляется возможным в силу того, что оба показателя являются динамичными и изменяются в зависимости от котировок цены актива и рынка. Можно лишь дать оценочное значение показателя на основе регрессионного анализа.
Теперь необходимо рассчитать все элементы, данные в формуле. Формула расчета бета-коэффициента приводилась в начале статьи. Альфа-коэффициент определяет доходность актива вне зависимости от динамики рынка. Рассчитывается как разность математического ожиданий доходности рынка в начале периода и доходности рынка в начале периода, помноженная на коэффиицент бета. Формула расчета следующая:
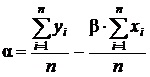 , где
, гдеyi, xi – доходность рынка в i период времени.
Последний элемент формулы – случайная погрешность. Этот индикатор указывает на возможную неточность модели Шарпа и является случайной переменной, имеющей нулевое математическое ожидание доходности и стандартное отклонение. Вычисляется по следующей формуле:
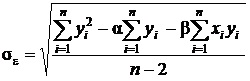
Еще немного стоит уточнить про коэффициент бета. Данный индикатор не может быть абсолютно точным, так как имеет стандартную ошибку – попытку оценить величину таких ошибок:
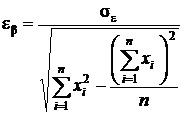
Иными словами, получается как бы замкнутый круг – бета-коэффициент по стандартной формуле пытается рассчитать величину стандартных ошибок, которая изменяется в зависимости от ценовой динамики актива и рынка. Аналогичная стандартная ошибка альфа-коэффициент дает оценку отклонения прогнозируемого значения цены от «истинного»:
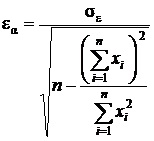
Еще один важный показатель, который часто применяют при расчете характеристик того или иного актива – коэффициент детерминации, или R2, однако об этом будет рассказано в одном из последующих материалов. В западных странах коэффициенты a, b и R2 рассчитываются для всех ценных бумаг регулярно и публикуются вместе с рыночными индексами. Фактически, данные показатели позволяют инвесторам самостоятельно разработать инвестиционный портфель.
Теперь же постараемся обобщить материал непосредственно по модели Уильяма Шарпа. Итак, цель данной модели – упростить линейные методы построения инвестиционных портфелей и регрессионного анализа за счет использования индексов (то есть доходности бенчмарка – фондового индекса либо индивидуально построенного рыночного индекса). Для этого проводится регрессионный анализ – то есть анализируются исторические данные котировок конкретного актива и рынка. При этом ставится задача выявить зависимость изменения цены актива от динамики бенчмарка и исходя из этого рассчитать в конечном итоге коэффициент риска, который станет индикатором актуальности инвестирования в актив. Вот собственно и все. В одном из последующих статей будет выложен конкретный пример расчета коэффициента Шарпа и его использования непосредственно при построении портфеля.
Не является индивидуальной инвестиционной рекомендацией | При копировании ссылка обязательна | Нашли ошибку - выделить и нажать Ctrl+Enter | Жалоба

