29 ноября 2018 smart-lab.ru
О "нормальном рынке" или "Что Вы хотите узнать про опционы, но боитесь спросить?"
Некоторое время назад столкнулся на С-Л со странным явлением "отрицания наблюдаемых фактов". Причем ладно бы дело касалось вопросов веры. Или вопросов политики — там эта картина ожидаема. Но в среде практикующих трейдеров это было неожиданно.
Чтобы быть конкретным, речь идет о природе рынка и о тех вероятностных законах, которые создают график цен.
Было высказано утверждение о том, что "фундаментальный процесс, создающий график цены, является лог-нормальным броуновским движением".
При попытке указать на очевидные наблюдаемые различия использовались 2 линии возражений:
«надо немножко подождать и рынок станет нормальным»
«рынок является нестационарным нормальным»
Возникло желание еще раз коснуться вопроса в рамках вебинара "TSLab Опционы", который состоится в этот четверг 25 октября 2018 года в 11:00 на платформе Красный Циркуль.
В прошлый раз посмотрели эмпирическое распределение индекса RTSI на недельном таймфрейме.
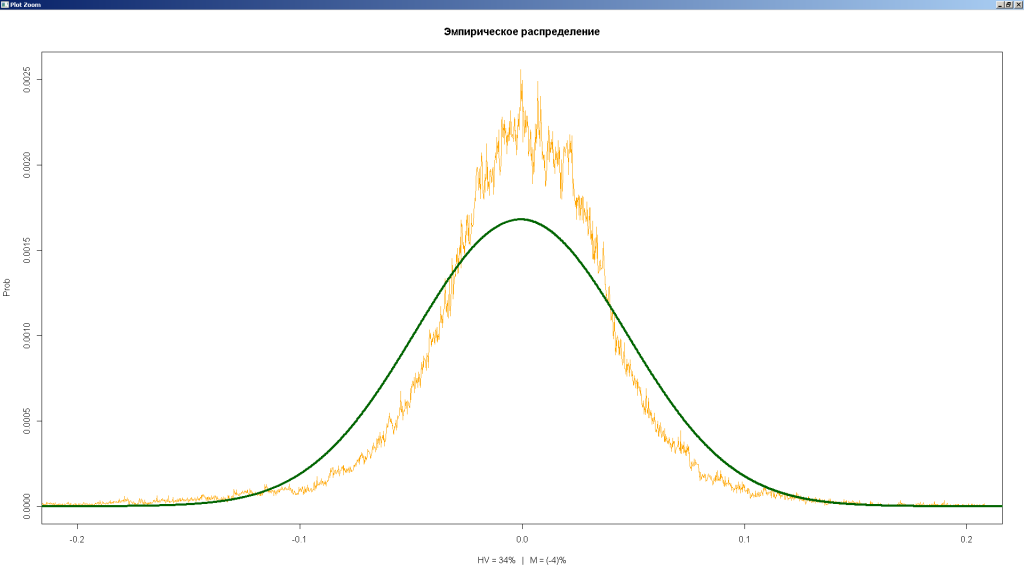
В четверг (как обещал) посмотрим распределение для USD/RUB.
Чтобы общение получилось более полезным, предлагаю желающим написать в комментарии к этому топику свои вопросы в духе "Что я хочу узнать про опционы, но никак не дойдут руки разобраться?"
https://smart-lab.ru/blog/501059.php
В поисках Истины или Почему мы вычисляем именно матожидание?
Некоторое время назад после подробного обсуждения с коллегами вопроса "Нормален ли рынок и если ненормален, то какой он на самом деле?" от других коллег прозвучало недоумение: "А зачем тебе копаться в этих дебрях? Какой в этом смысл?". Короткий ответ будет неполным, а полный ответ с примерами и философским вопросом может оказаться интересен (или даже полезен коллегам).
1. Итак. Быстрый ответ состоит в разнице инженерного (институтского) и научного (университетского) мышления.
Как работает инженерное мышление: в институе студентам дали формулу и надрессировали ее применять. И они будут лепить ее везде. С огромной эффективностью и высокой скоростью. Пока самолеты не начнут падать. И тогда может выясниться, что у формулы были примечания мелким шрифтом. Ограничения области применимости.
Как работает научное мышление: необходимо не просто запомнить формулу (зачастую даже собственно запоминание формулы даже не является целью изучения вопроса). Фокус будет находиться на методе получения этой формулы. Причем должны быть абсолютно прояснены все подробности: почему? откуда это следует? какие есть ограничения? и т.д.
Обладая таким багажом ученый не просто лепит Формулу направо и налево. Он садится, вникает в предмет. В условия функционирования системы. При необходимости понимает в чем отличие конкретной текущей ситуации от классических уже известных случаев. При необходимости ученый повторяет все этапы известного ему метода индукции с новыми вводными и получает новую формулу. Конкретно для данного случая.
В опционном мире это будет выглядеть так:
Инженер: а! Формула Блека-Шолза на Википедии. Там есть формулы для греков. Подставляем. Дельта моей позиции 50, гамма 0.000500. Блин, а почему я постоянно сливаю? Я же купил по теорцене биржи!?!?!?
Ученый: формула Б-Ш? Хм! Чето она мне не нравится. А, понятно: формула верна только при постоянной сигме. Сажусь считаю как положено в условиях наличия улыбки. Ну, страшноватые формулки в результате. Но ничего. Компьютеры теперь быстро считают. Подставляем. Дельта позиции Инженера 45, гамма 0.000350. Ну, понятно почему он сливает: потому что дельта у него неправильная аж на 5 единиц.
2. Пример пользы от копания в разделе «сноски» где много мелкого шрифта.
Нам всем прожужжали уши про то, что «рынок эффективен и непредсказуем и куда он пойдет никто не знает». Вверх или вниз — 50-на-50. Как в анекдоте про блондинку и динозавра. Что это будет означать на опционном языке в идеальном мире Блека-Шолза? Интуитивно возникает ощущение, что это будет означать симметричность распределения для логарифмов цен. Вверх на 5% так же вероятно, что вниз на 5%. Именно в этом будет выражаться равноправие направлений вверх и вниз. Логично? Все согласны?
Отлично.
Теперь вспоминаем, что нас в умных книжках научили, что цена опциона равна матожиданию выплат на дату экспирации:
CALL = E [ CallPay ]
Подставляем, интегрируем и получаем, что опционы будут в разы дороже, а путы в разы дешевле наблюдаемых на рынке цен. Почему? Потому что распределение цены получается как "экспонента от логарифмов". Выражаяь простым языком лог-нормальное.
Так в чем подвох? Подвох в том, что лог-нормальное распределение крайне несимметрично. У просто нормального распределения совпадают основные характеристики: среднее, мода и медиана. У логнормального распределения они существенно разные.
В частности, среднее равно exp(+0.5*sigma*sigma)
А при таком среднем путы никому не нужны. Покупай колы (или просто базу) — рынок в целом всегда растет — колы колосятся и наливаются прибылью.
И тут как раз идет сноска мелким шрифтом: чтобы восстановить справедливость (и испортить сон всем долгосрочным инвесторам) нужно в исходное распределение логарифмов добавить ОТРИЦАТЕЛЬНЫЙ ДРЕЙФ в размере ровно (-0.5*sigma*sigma). При типичной сигме 30% годовых это будет (-4.5%) годовых. Обычно, эту сноску прячут за умным словом "лемма Ито". Кто-то копался в этой лемме? Разбирался почему ее применяют направо и налево? Вряд ли. Получите и распишитесь. Привет всем долгосрочным инвесторам! Вы думаете, что "рынок всегда растет"? Вот незадача. А рынок думает, что он ВСЕГДА ПАДАЕТ. На (-4.5%) в год!
А почему же тогда рынки периодически штурумуют новые вершины? С чисто математической точки зрения в этом идеальном мире это вызвано как раз резкой асимметрией логнормального распределения. У него всегда есть вероятность получить очень большой плюс. Хоть и с маленькой вероятностью. Думаю, теперь понятно почему так трудно ловить аптренды в акциях и индексах? Они бывают. И рост бывает феноменальным. Но редко. Кто и где выстрелит в следующий раз — об этом в идеальном мире Блека-Шолза не знают даже сами эти акции.
А теперь главный вопрос записи.
3. Почему для получения «справедливой цены опциона» мы вычисляем именно математическое ожидание?
Прошу коллег опционщиков ( Каленкович Алексей (enki) , bstone, Дмитрий Новиков , Стас Бржозовский , Борис Боос , Московский Лоссбой , А. Г. , Юрий М. , Дон Маттео , Rustem, KLoYH, Кирилл Браулов, baron_samedi, wrmngr, НеГрустин ) а также любителей задачек ( Мальчик Buybuy , FZF , Sergey Pavlov , anatolyutkin , Борис Гудылин , ivanovr , toshackers , Zверобой ) высказать свои соображения на этот счет. Лично я вдруг понял, что не понимаю этого (неудовлетворительно понимаю даже после размышлений над этим). Может быть, это можно разобрать на каких-то простых примерах типа лотерей с некими правилами участия?
Если это является следствием каких-то соображений о «справедливости» или «равновесности» системы? Тогда в чем состоят эти соображения? Почему в качестве цены не берется медиана или мода? Или какая-то другая характеристика или более сложная функция от выплат? Наконец, почему опцион рассматривается в изоляции от других факторов (мы же понимаем, что как минимум всегда существует базовый актив и всегда существует опцион другого типа на том же страйке, а также существуют другие опционы на тот же базовый актив)?
https://smart-lab.ru/blog/505349.php
Ненормальные опционщики
Огромное человеческое спасибо всем, кто участвовал в обсуждении нормальности рынка и матожидания. Надеюсь, оно было полезно не только мне и количество людей осознавших, что "реальный рынок НЕ является лог-нормальным случайным блужданием" (даже с оговорками про нормировку на текущую волатильность по причине ненаблюдаемости последней) увеличилось.
Но опционщики — парни ловкие (а девушки еще и красивые).
Дело в том, что опционные позиции — это на самом деле преобразования функции плотности рыночного распределения. Давно грезил этой мыслью (собственно, идея достаточно очевидна и бесспорна). Но только недавно (в том числе благодаря обсуждениям природы рынка) удалось продвинуться в этом направлении.
Давайте достанем из старого шкафа старую поеденную молью модель Блека-Шолза . Принудительно перенесемся в этот сказочно прекрасный мир, в котором рынок является лог-нормальным броуновским блужданием и построим в этом прекрасном сверкающем мире парочку позиций. Начнем с простого, потом усложним и, надеюсь, сила искусства будет достаточна, чтобы даже у великих ( А. Г. ) не было сомнений и возражений, что опционщики живут в существенно негауссовом мире . Настолько негауссовом, что его нельзя назвать даже "нестационарно нормальным".
Стартовые условия
до экспирации ровно 1 год ( dT = 1 )
текущая цена фьючерса Fo = 100 000
волатильность 30% годовых ( sigma = 0.3 )
центральный страйк K = 100 000
безрисковая ставка 0 (как обычно для опционов на фьючерсы)
Формируем позицию, хеджируем (или не хеджируем) в первый момент времени, симулируем возможные траектории движения цены на разные моменты времени внутри этого года (возьмем шаг 1 календарные сутки) смотрим куда придет рынок, переоцениваем свой портфель, строим гистограмму. Чтобы числа не зависели от формы позиции, гистограмму строим не для цен позиции, а для прибыли портфеля. Таким образом, возникает выделенный 0 (будет отмечен вертикальной голубой линией). Дополнительно меня будет интересовать медиана всех траекторий. То есть результат, который мы будем наблюдать в 50% случаев. Отмечен вертикальной красной линией.
Размышляем и делаем выводы.
1. Купленный фьючерс
Это очередной привет всем долгосрочным инвесторам. Мало того, что в мире БШ Вы сидите под отрицательным дрейфом цены, так еще и позиция уходит в минус больше, чем в половине случаев. На (-4400) или хуже.
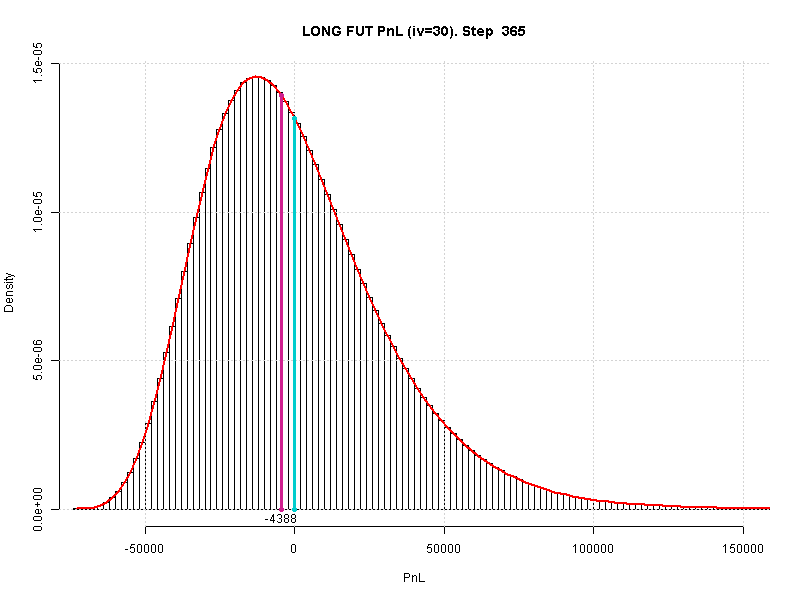
Хуже всего, что на самом деле финрез инвестора, грубо говоря, "какой угодно". И чем больше времени держать лонг, тем шире будет становиться этот колокол.
2. Проданный фьючерс
Распределение проданного фьючерса недвусмысленно объясняет, почему эти позиции называют короткими. Зашортил, чуть-чуть подержал, закрыл с прибылью. Потому что если держать шорт долго, то он может принести убыток бОльший, чем первоначальная цена продажи. Например, (-150 000).
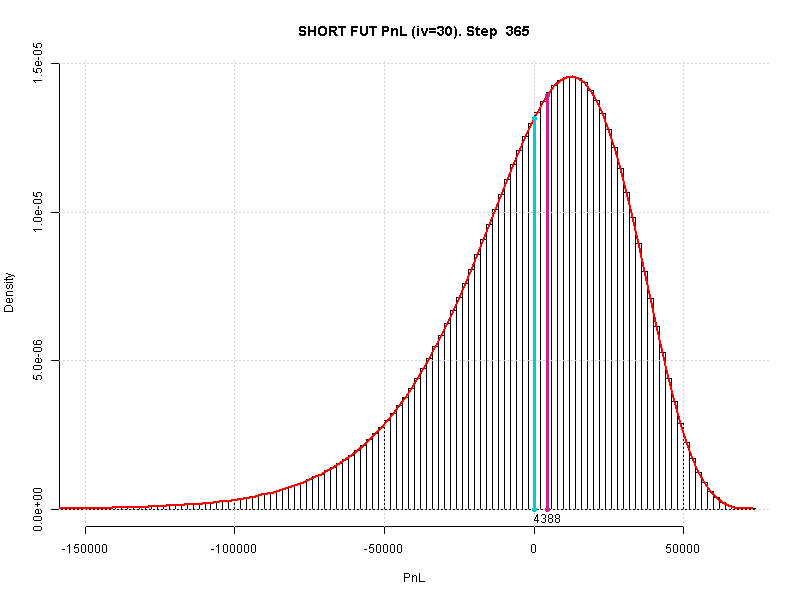
И еще из этого графика видно, почему многие гуру любят давать сигналы именно на шорт. Что бы ни случилось — всегда говорят, что "скоро упадет". Потому что сигнал на шорт, взятый без учета величины возможного убытка, автоматически сбывается где-то примерно в 55% случаев. То есть можно с чистой совестью утверждать, что "я чаще прав, чем ошибаюсь".
3. Купленный стреддл на-деньгах
Но возвращаемся к опционам.
Второе, что приходит в голову — купленный стреддл на-деньгах (захеджированный в первый момент времени).
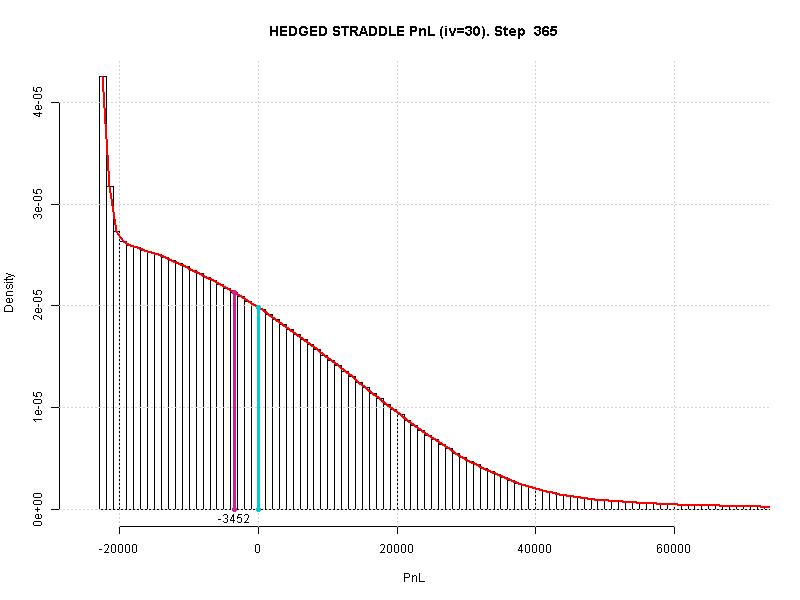
Медиана поднялась с (-4400) до (-3500). Жестко отграничен убыток размером первоначальной премии (примерно 24 000 для позиции +1 пут +1 колл). Достижимые прибыли не очень сильно упали. По-прежнему можно стать обладателем чистой прибыли в размере 1-2 первоначальные премии (удвоение ставки позиции за год!).
Это распределение не похоже на классический колокол. Оно явно не нормальное. Оно явно не лог-нормальное.
То есть покупатель стреддла связывает жизнь своего депозита с крайне ненормальным распределением.
Без подробностей скажу, что внимательное отслеживание судьбы этой позиции показывает, что она сначала проваливается в минус и довольно долго там находится. Медиана может опуститься до (-5000), но затем начинает расти до (-3500).
Из этого также следует, что при работе с купленным стреддлом надо сидеть в нем как можно меньше. Взял, подержал, получил хорошую прибыль — зафиксировал. Нет — борешься за нуль в лучшем случае.
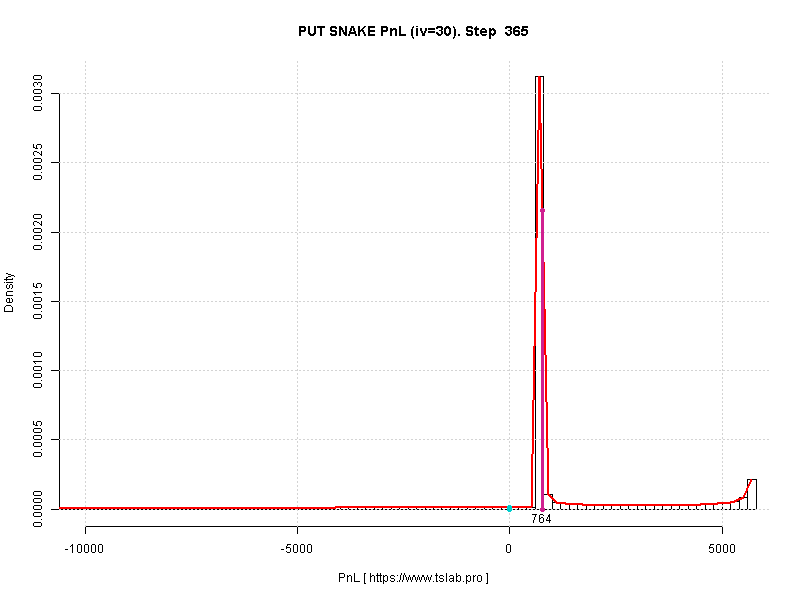
4. Опционная змея (на путах)
Крайняя степень искажения распределения. Исходный колокол превратился в двумодальное распределение с исчезающей вероятностью убытка на день экспирации (правда, размер этого убытка может в 10 и более раз превосходить самую вероятную прибыль).
Некоторое время назад столкнулся на С-Л со странным явлением "отрицания наблюдаемых фактов". Причем ладно бы дело касалось вопросов веры. Или вопросов политики — там эта картина ожидаема. Но в среде практикующих трейдеров это было неожиданно.
Чтобы быть конкретным, речь идет о природе рынка и о тех вероятностных законах, которые создают график цен.
Было высказано утверждение о том, что "фундаментальный процесс, создающий график цены, является лог-нормальным броуновским движением".
При попытке указать на очевидные наблюдаемые различия использовались 2 линии возражений:
«надо немножко подождать и рынок станет нормальным»
«рынок является нестационарным нормальным»
Возникло желание еще раз коснуться вопроса в рамках вебинара "TSLab Опционы", который состоится в этот четверг 25 октября 2018 года в 11:00 на платформе Красный Циркуль.
В прошлый раз посмотрели эмпирическое распределение индекса RTSI на недельном таймфрейме.

В четверг (как обещал) посмотрим распределение для USD/RUB.
Чтобы общение получилось более полезным, предлагаю желающим написать в комментарии к этому топику свои вопросы в духе "Что я хочу узнать про опционы, но никак не дойдут руки разобраться?"
https://smart-lab.ru/blog/501059.php
В поисках Истины или Почему мы вычисляем именно матожидание?
Некоторое время назад после подробного обсуждения с коллегами вопроса "Нормален ли рынок и если ненормален, то какой он на самом деле?" от других коллег прозвучало недоумение: "А зачем тебе копаться в этих дебрях? Какой в этом смысл?". Короткий ответ будет неполным, а полный ответ с примерами и философским вопросом может оказаться интересен (или даже полезен коллегам).
1. Итак. Быстрый ответ состоит в разнице инженерного (институтского) и научного (университетского) мышления.
Как работает инженерное мышление: в институе студентам дали формулу и надрессировали ее применять. И они будут лепить ее везде. С огромной эффективностью и высокой скоростью. Пока самолеты не начнут падать. И тогда может выясниться, что у формулы были примечания мелким шрифтом. Ограничения области применимости.
Как работает научное мышление: необходимо не просто запомнить формулу (зачастую даже собственно запоминание формулы даже не является целью изучения вопроса). Фокус будет находиться на методе получения этой формулы. Причем должны быть абсолютно прояснены все подробности: почему? откуда это следует? какие есть ограничения? и т.д.
Обладая таким багажом ученый не просто лепит Формулу направо и налево. Он садится, вникает в предмет. В условия функционирования системы. При необходимости понимает в чем отличие конкретной текущей ситуации от классических уже известных случаев. При необходимости ученый повторяет все этапы известного ему метода индукции с новыми вводными и получает новую формулу. Конкретно для данного случая.
В опционном мире это будет выглядеть так:
Инженер: а! Формула Блека-Шолза на Википедии. Там есть формулы для греков. Подставляем. Дельта моей позиции 50, гамма 0.000500. Блин, а почему я постоянно сливаю? Я же купил по теорцене биржи!?!?!?
Ученый: формула Б-Ш? Хм! Чето она мне не нравится. А, понятно: формула верна только при постоянной сигме. Сажусь считаю как положено в условиях наличия улыбки. Ну, страшноватые формулки в результате. Но ничего. Компьютеры теперь быстро считают. Подставляем. Дельта позиции Инженера 45, гамма 0.000350. Ну, понятно почему он сливает: потому что дельта у него неправильная аж на 5 единиц.
2. Пример пользы от копания в разделе «сноски» где много мелкого шрифта.
Нам всем прожужжали уши про то, что «рынок эффективен и непредсказуем и куда он пойдет никто не знает». Вверх или вниз — 50-на-50. Как в анекдоте про блондинку и динозавра. Что это будет означать на опционном языке в идеальном мире Блека-Шолза? Интуитивно возникает ощущение, что это будет означать симметричность распределения для логарифмов цен. Вверх на 5% так же вероятно, что вниз на 5%. Именно в этом будет выражаться равноправие направлений вверх и вниз. Логично? Все согласны?
Отлично.
Теперь вспоминаем, что нас в умных книжках научили, что цена опциона равна матожиданию выплат на дату экспирации:
CALL = E [ CallPay ]
Подставляем, интегрируем и получаем, что опционы будут в разы дороже, а путы в разы дешевле наблюдаемых на рынке цен. Почему? Потому что распределение цены получается как "экспонента от логарифмов". Выражаяь простым языком лог-нормальное.
Так в чем подвох? Подвох в том, что лог-нормальное распределение крайне несимметрично. У просто нормального распределения совпадают основные характеристики: среднее, мода и медиана. У логнормального распределения они существенно разные.
В частности, среднее равно exp(+0.5*sigma*sigma)
А при таком среднем путы никому не нужны. Покупай колы (или просто базу) — рынок в целом всегда растет — колы колосятся и наливаются прибылью.
И тут как раз идет сноска мелким шрифтом: чтобы восстановить справедливость (и испортить сон всем долгосрочным инвесторам) нужно в исходное распределение логарифмов добавить ОТРИЦАТЕЛЬНЫЙ ДРЕЙФ в размере ровно (-0.5*sigma*sigma). При типичной сигме 30% годовых это будет (-4.5%) годовых. Обычно, эту сноску прячут за умным словом "лемма Ито". Кто-то копался в этой лемме? Разбирался почему ее применяют направо и налево? Вряд ли. Получите и распишитесь. Привет всем долгосрочным инвесторам! Вы думаете, что "рынок всегда растет"? Вот незадача. А рынок думает, что он ВСЕГДА ПАДАЕТ. На (-4.5%) в год!
А почему же тогда рынки периодически штурумуют новые вершины? С чисто математической точки зрения в этом идеальном мире это вызвано как раз резкой асимметрией логнормального распределения. У него всегда есть вероятность получить очень большой плюс. Хоть и с маленькой вероятностью. Думаю, теперь понятно почему так трудно ловить аптренды в акциях и индексах? Они бывают. И рост бывает феноменальным. Но редко. Кто и где выстрелит в следующий раз — об этом в идеальном мире Блека-Шолза не знают даже сами эти акции.
А теперь главный вопрос записи.
3. Почему для получения «справедливой цены опциона» мы вычисляем именно математическое ожидание?
Прошу коллег опционщиков ( Каленкович Алексей (enki) , bstone, Дмитрий Новиков , Стас Бржозовский , Борис Боос , Московский Лоссбой , А. Г. , Юрий М. , Дон Маттео , Rustem, KLoYH, Кирилл Браулов, baron_samedi, wrmngr, НеГрустин ) а также любителей задачек ( Мальчик Buybuy , FZF , Sergey Pavlov , anatolyutkin , Борис Гудылин , ivanovr , toshackers , Zверобой ) высказать свои соображения на этот счет. Лично я вдруг понял, что не понимаю этого (неудовлетворительно понимаю даже после размышлений над этим). Может быть, это можно разобрать на каких-то простых примерах типа лотерей с некими правилами участия?
Если это является следствием каких-то соображений о «справедливости» или «равновесности» системы? Тогда в чем состоят эти соображения? Почему в качестве цены не берется медиана или мода? Или какая-то другая характеристика или более сложная функция от выплат? Наконец, почему опцион рассматривается в изоляции от других факторов (мы же понимаем, что как минимум всегда существует базовый актив и всегда существует опцион другого типа на том же страйке, а также существуют другие опционы на тот же базовый актив)?
https://smart-lab.ru/blog/505349.php
Ненормальные опционщики
Огромное человеческое спасибо всем, кто участвовал в обсуждении нормальности рынка и матожидания. Надеюсь, оно было полезно не только мне и количество людей осознавших, что "реальный рынок НЕ является лог-нормальным случайным блужданием" (даже с оговорками про нормировку на текущую волатильность по причине ненаблюдаемости последней) увеличилось.
Но опционщики — парни ловкие (а девушки еще и красивые).
Дело в том, что опционные позиции — это на самом деле преобразования функции плотности рыночного распределения. Давно грезил этой мыслью (собственно, идея достаточно очевидна и бесспорна). Но только недавно (в том числе благодаря обсуждениям природы рынка) удалось продвинуться в этом направлении.
Давайте достанем из старого шкафа старую поеденную молью модель Блека-Шолза . Принудительно перенесемся в этот сказочно прекрасный мир, в котором рынок является лог-нормальным броуновским блужданием и построим в этом прекрасном сверкающем мире парочку позиций. Начнем с простого, потом усложним и, надеюсь, сила искусства будет достаточна, чтобы даже у великих ( А. Г. ) не было сомнений и возражений, что опционщики живут в существенно негауссовом мире . Настолько негауссовом, что его нельзя назвать даже "нестационарно нормальным".
Стартовые условия
до экспирации ровно 1 год ( dT = 1 )
текущая цена фьючерса Fo = 100 000
волатильность 30% годовых ( sigma = 0.3 )
центральный страйк K = 100 000
безрисковая ставка 0 (как обычно для опционов на фьючерсы)
Формируем позицию, хеджируем (или не хеджируем) в первый момент времени, симулируем возможные траектории движения цены на разные моменты времени внутри этого года (возьмем шаг 1 календарные сутки) смотрим куда придет рынок, переоцениваем свой портфель, строим гистограмму. Чтобы числа не зависели от формы позиции, гистограмму строим не для цен позиции, а для прибыли портфеля. Таким образом, возникает выделенный 0 (будет отмечен вертикальной голубой линией). Дополнительно меня будет интересовать медиана всех траекторий. То есть результат, который мы будем наблюдать в 50% случаев. Отмечен вертикальной красной линией.
Размышляем и делаем выводы.
1. Купленный фьючерс
Это очередной привет всем долгосрочным инвесторам. Мало того, что в мире БШ Вы сидите под отрицательным дрейфом цены, так еще и позиция уходит в минус больше, чем в половине случаев. На (-4400) или хуже.

Хуже всего, что на самом деле финрез инвестора, грубо говоря, "какой угодно". И чем больше времени держать лонг, тем шире будет становиться этот колокол.
2. Проданный фьючерс
Распределение проданного фьючерса недвусмысленно объясняет, почему эти позиции называют короткими. Зашортил, чуть-чуть подержал, закрыл с прибылью. Потому что если держать шорт долго, то он может принести убыток бОльший, чем первоначальная цена продажи. Например, (-150 000).

И еще из этого графика видно, почему многие гуру любят давать сигналы именно на шорт. Что бы ни случилось — всегда говорят, что "скоро упадет". Потому что сигнал на шорт, взятый без учета величины возможного убытка, автоматически сбывается где-то примерно в 55% случаев. То есть можно с чистой совестью утверждать, что "я чаще прав, чем ошибаюсь".
3. Купленный стреддл на-деньгах
Но возвращаемся к опционам.
Второе, что приходит в голову — купленный стреддл на-деньгах (захеджированный в первый момент времени).

Медиана поднялась с (-4400) до (-3500). Жестко отграничен убыток размером первоначальной премии (примерно 24 000 для позиции +1 пут +1 колл). Достижимые прибыли не очень сильно упали. По-прежнему можно стать обладателем чистой прибыли в размере 1-2 первоначальные премии (удвоение ставки позиции за год!).
Это распределение не похоже на классический колокол. Оно явно не нормальное. Оно явно не лог-нормальное.
То есть покупатель стреддла связывает жизнь своего депозита с крайне ненормальным распределением.
Без подробностей скажу, что внимательное отслеживание судьбы этой позиции показывает, что она сначала проваливается в минус и довольно долго там находится. Медиана может опуститься до (-5000), но затем начинает расти до (-3500).
Из этого также следует, что при работе с купленным стреддлом надо сидеть в нем как можно меньше. Взял, подержал, получил хорошую прибыль — зафиксировал. Нет — борешься за нуль в лучшем случае.
4. Опционная змея (на путах)
Крайняя степень искажения распределения. Исходный колокол превратился в двумодальное распределение с исчезающей вероятностью убытка на день экспирации (правда, размер этого убытка может в 10 и более раз превосходить самую вероятную прибыль).

Не является индивидуальной инвестиционной рекомендацией | При копировании ссылка обязательна | Нашли ошибку - выделить и нажать Ctrl+Enter | Жалоба

