19 февраля 2020 smart-lab.ru
ечь пойдёт об одной из модификаций модели Блэка-Шоулза, известной как «Uncertain Volatility Model», «volatility band» или «Black-Scholes-Barenblatt model». Я кратко расскажу о модели, приведу простейшую реализацию на языке R, а также список наиболее полезных статей, касающихся этой модели.
Уравнение Блэка-Шоулза-Баренблатта
Используются все те же самые предположения, что и в модели Блэка-Шоулза, за одним исключением: про волатильность известно лишь то, в каком диапазоне она находится: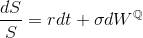
; 
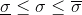. Очевидно, что при условии 
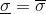эта модель должна быть эквивалентна модели Блэка-Шоулза.
Верхняя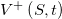
и нижняя 
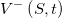границы цен опционов в рамках этой модели удовлетворяют следующему дифференциальному уравнению в частных производных:
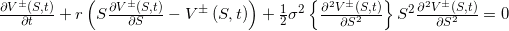
Наиболее существенным отличием от обычного уравнения Блэка-Шоулза является то, что волатильность зависит от гаммы опциона: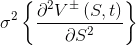
.
А именно, следующим образом:
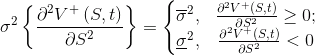
Реализация
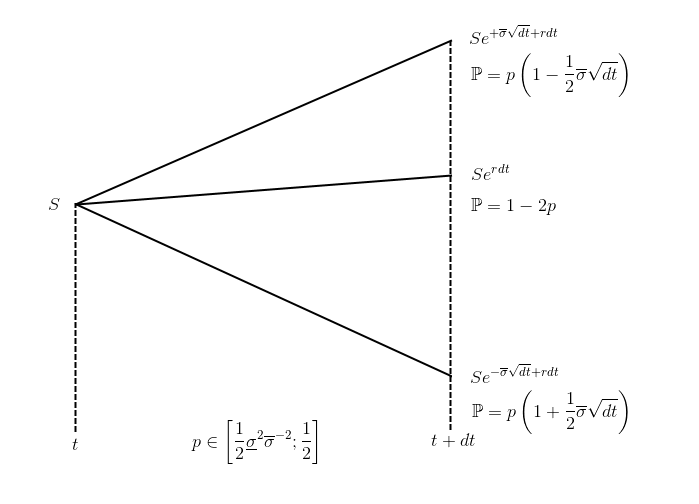
Расчёт цен опционов в рамках данной модели может быть выполнен при помощи триномиальных деревьев с рекомбинацией:
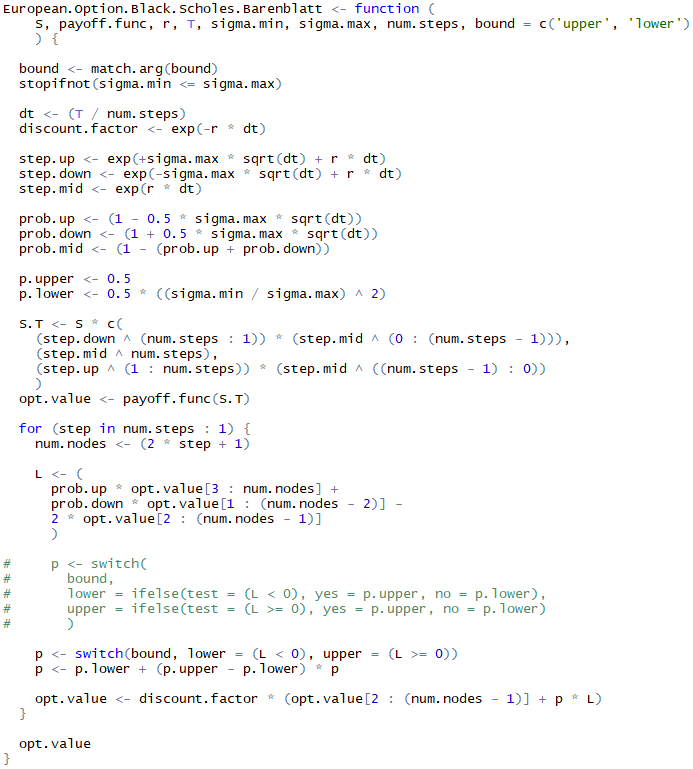
Для тех, кто не очень разбирается в подобных методах — вот простейшая реализация оценивания опционов в рамках модели Блэка-Шоулза с использованием биномиальных деревьев (известна также как модель Кокса-Росса-Рубинштейна):
Объяснение идеи «на пальцах»:
1. Строим дерево возможных траекторий цены, сдвигаясь из каждого узла на каждом шаге вверх на step.up с вероятностью prob.up, либо вниз на step.down с вероятностью prob.down;
2. Считаем выплаты по опциону для каждой цены на момент экспирации;
3. Двигаемся от экспирации в сторону текущего момента времени, определяя цену опциона в промежуточных узлах как дисконтированное матожидание возможных стоимостей в следующий момент времени.
А теперь вернёмся обратно к оцениванию опционов при неопределенной волатильности:
В целом — всё то же самое, с небольшими отличиями:
1. Используется более сложное дерево (схему одного шага см. в начале части);
2. При определении цен в промежуточных узлах учитывается знак гаммы опциона.
Примеры
Стоимость европейского опциона типа «колл» со страйком 110, временем до экспирации 0.25 (года), безрисковой ставкой 2%, диапазоном для волатильности 15..40%, в зависимости от цены базового актива. Для сравнения также сосчитаны цены с использованием модели Кокса-Росса-Рубинштейна, по верхней и нижней границам волатильности. Кол-во шагов в деревьях — 1000.
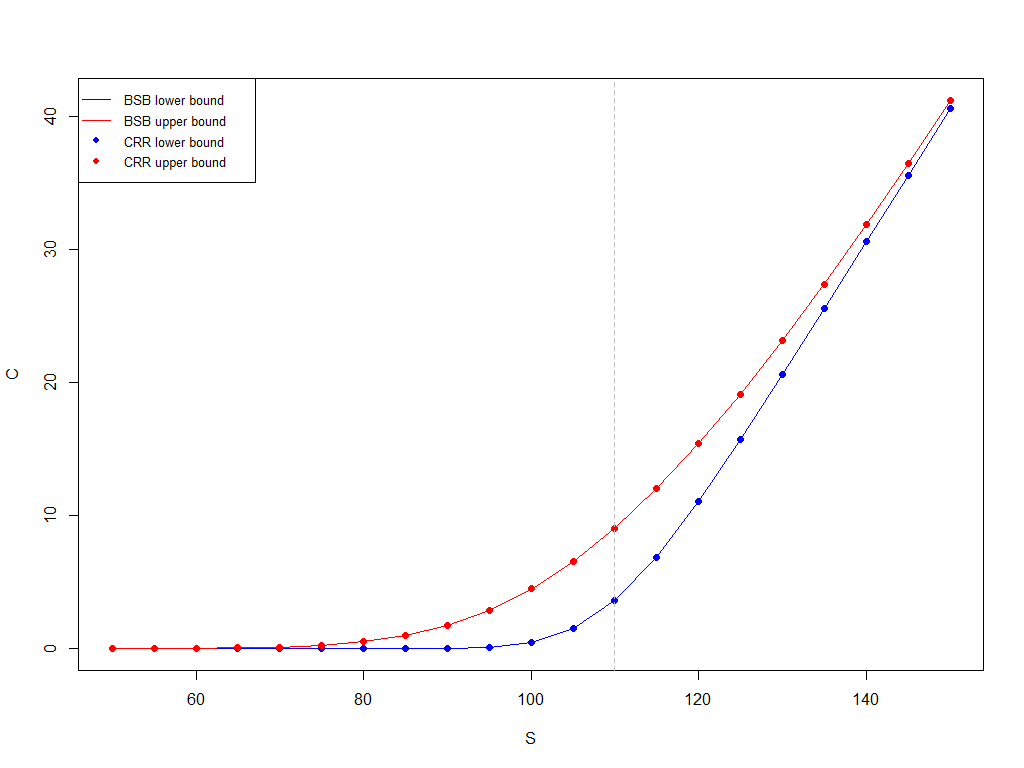
В этом случае цены, получаемые по модели Блэка-Шоулза-Баренблатта, совпадают с ценами, получаемыми по модели Кокса-Росса-Рубинштейна (а, значит, и с ценами, получаемыми по модели Блэка-Шоулза).
Рассмотрим бычий колл-спред 100-110. Для оценивания нижней границы цены колл-спреда в рамках модели Кокса-Росса-Рубинштейна будем использовать нижнюю границу волатильности для получения цены покупаемых опционов, и верхнюю границу волатильности для получения цены продаваемых опционов. Для верхней границы всё наоборот: верхняя граница волатильности для покупаемых опционов, нижняя граница волатильности для получения цены продаваемых опционов. А вот в модель Блэка-Шоулза-Баренблатта мы запихнём контрактную функцию колл-спреда целиком. Вуаля!
В случае с конструкциями, компоненты которых имеют гамму разных знаков, оценивание их целиком даёт гораздо более узкий интервал возможных цен. Sapienti sat.
Напоследок
Исходный код: https://pastebin.com/A9YwwATz
Верхняя и нижняя границы волатильности могут быть модифицированы для учёта транзакционных издержек при дельта-хеджировании. Подробности ищите в статье [1] из списка литературы.
Литература
1. Marco Avellaneda, Antonio Paras «Managing the Volatility Risk of Portfolios of Derivative Securities: The Lagrangian Uncertain Volatility Model»
2. Marco Avellaneda «An Introduction to Option Pricing and the Mathematical Theory of Risk»
3. Anna Kolesnichenko, Galina Shopina «Valuation of portfolios under uncertain volatility: Black-Scholes-Barenblatt equations and the static hedging»; technical report
4. Alena Sdobnova, Jakub Blaszkiewics «Analysis of An Uncertain Volatility Model in the framework of static hedging for different scenarios»; technical report
5. David Pooley «Numerical Methods for Nonlinear Equations in Option Pricing»; PhD thesis
6. Albrecht Budke «Finite Difference Methods for the Non-linear Black-Scholes-Barenblatt Equation»; PhD thesis
7. Claude Martini, Antoine Jacquier «The Uncertain Volatility Model»
8. Swati Mital «Uncertain Volatility Model»; June 6, 2016
9. Xinpeng Li, Yiqing Lin, Weicheng Xu «On properties of solutions to Black-Scholes-Barenblatt equations»; Advances in Difference equations 2019:193
10. Gunter H. Meyer «The Black Scholes Barenblatt Equations for Options with Uncertain Volatility and its Application to Static Hedging»; Working paper, October 2004
Уравнение Блэка-Шоулза-Баренблатта
Используются все те же самые предположения, что и в модели Блэка-Шоулза, за одним исключением: про волатильность известно лишь то, в каком диапазоне она находится:
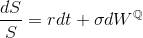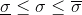; . Очевидно, что при условии 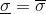эта модель должна быть эквивалентна модели Блэка-Шоулза.Верхняя
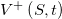и нижняя 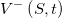границы цен опционов в рамках этой модели удовлетворяют следующему дифференциальному уравнению в частных производных: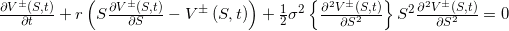Наиболее существенным отличием от обычного уравнения Блэка-Шоулза является то, что волатильность зависит от гаммы опциона:
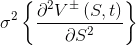.А именно, следующим образом:
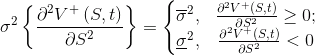
Реализация
Расчёт цен опционов в рамках данной модели может быть выполнен при помощи триномиальных деревьев с рекомбинацией:
Для тех, кто не очень разбирается в подобных методах — вот простейшая реализация оценивания опционов в рамках модели Блэка-Шоулза с использованием биномиальных деревьев (известна также как модель Кокса-Росса-Рубинштейна):
Объяснение идеи «на пальцах»:
1. Строим дерево возможных траекторий цены, сдвигаясь из каждого узла на каждом шаге вверх на step.up с вероятностью prob.up, либо вниз на step.down с вероятностью prob.down;
2. Считаем выплаты по опциону для каждой цены на момент экспирации;
3. Двигаемся от экспирации в сторону текущего момента времени, определяя цену опциона в промежуточных узлах как дисконтированное матожидание возможных стоимостей в следующий момент времени.
А теперь вернёмся обратно к оцениванию опционов при неопределенной волатильности:
В целом — всё то же самое, с небольшими отличиями:
1. Используется более сложное дерево (схему одного шага см. в начале части);
2. При определении цен в промежуточных узлах учитывается знак гаммы опциона.
Примеры
Стоимость европейского опциона типа «колл» со страйком 110, временем до экспирации 0.25 (года), безрисковой ставкой 2%, диапазоном для волатильности 15..40%, в зависимости от цены базового актива. Для сравнения также сосчитаны цены с использованием модели Кокса-Росса-Рубинштейна, по верхней и нижней границам волатильности. Кол-во шагов в деревьях — 1000.
В этом случае цены, получаемые по модели Блэка-Шоулза-Баренблатта, совпадают с ценами, получаемыми по модели Кокса-Росса-Рубинштейна (а, значит, и с ценами, получаемыми по модели Блэка-Шоулза).
Рассмотрим бычий колл-спред 100-110. Для оценивания нижней границы цены колл-спреда в рамках модели Кокса-Росса-Рубинштейна будем использовать нижнюю границу волатильности для получения цены покупаемых опционов, и верхнюю границу волатильности для получения цены продаваемых опционов. Для верхней границы всё наоборот: верхняя граница волатильности для покупаемых опционов, нижняя граница волатильности для получения цены продаваемых опционов. А вот в модель Блэка-Шоулза-Баренблатта мы запихнём контрактную функцию колл-спреда целиком. Вуаля!
В случае с конструкциями, компоненты которых имеют гамму разных знаков, оценивание их целиком даёт гораздо более узкий интервал возможных цен. Sapienti sat.
Напоследок
Исходный код: https://pastebin.com/A9YwwATz
Верхняя и нижняя границы волатильности могут быть модифицированы для учёта транзакционных издержек при дельта-хеджировании. Подробности ищите в статье [1] из списка литературы.
Литература
1. Marco Avellaneda, Antonio Paras «Managing the Volatility Risk of Portfolios of Derivative Securities: The Lagrangian Uncertain Volatility Model»
2. Marco Avellaneda «An Introduction to Option Pricing and the Mathematical Theory of Risk»
3. Anna Kolesnichenko, Galina Shopina «Valuation of portfolios under uncertain volatility: Black-Scholes-Barenblatt equations and the static hedging»; technical report
4. Alena Sdobnova, Jakub Blaszkiewics «Analysis of An Uncertain Volatility Model in the framework of static hedging for different scenarios»; technical report
5. David Pooley «Numerical Methods for Nonlinear Equations in Option Pricing»; PhD thesis
6. Albrecht Budke «Finite Difference Methods for the Non-linear Black-Scholes-Barenblatt Equation»; PhD thesis
7. Claude Martini, Antoine Jacquier «The Uncertain Volatility Model»
8. Swati Mital «Uncertain Volatility Model»; June 6, 2016
9. Xinpeng Li, Yiqing Lin, Weicheng Xu «On properties of solutions to Black-Scholes-Barenblatt equations»; Advances in Difference equations 2019:193
10. Gunter H. Meyer «The Black Scholes Barenblatt Equations for Options with Uncertain Volatility and its Application to Static Hedging»; Working paper, October 2004
Не является индивидуальной инвестиционной рекомендацией | При копировании ссылка обязательна | Нашли ошибку - выделить и нажать Ctrl+Enter | Жалоба