Один из типов экономических задач — это задачи на платежи с равномерно убывающим долгом. Каждый месяц (период) основной долг уменьшается на одинаковую сумму. Ежемесячный платеж будет состоять из суммы основного долга и суммы начисленных процентов на остаток долга.
В этом случае мы имеем дело с дифференцированными платежами.
Внимание: в задачах этого типа применяется формула суммы n-первых членов арифметической прогрессии.
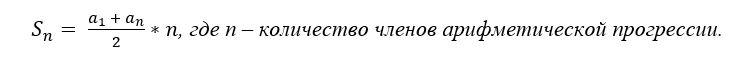
Задачи для разбора берутся из вариантов ЕГЭ прошлых лет, размещённых на популярном среди школьников и учителей сайте РЕШУ ЕГЭ.
Задача 1. Рассчитать сумму кредита
15 января планируется взять кредит в банке на 49 месяцев. Условия его возврата таковы:
1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
с 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Какую сумму следует взять в кредит, чтобы общая сумма выплат по кредиту после полного его погашения составила 2 млн руб. (никакие округления при вычислении платежей не производятся)?
Решение:
S тыс. руб. — сумма кредита,
р = 0,01,
2 млн руб. = 2000 тыс. руб.,
X тыс. руб. — ежемесячная выплата основного долга.
Суммы ежемесячного долга: S; (S — X); (S — 2 * X ... S — 47 * X); (S — 48 * X); 0
Начисленные проценты: S * p; (S — X) * p; (S — 2 * X) * p ... (S — 47 * X) * p; (S — 48 * X) * p; 0
Сумма выплат = Сумма кредита + Проценты
S + S * p + (S — X) * p + (S — 2 * X) * p + ...+ (S — 47 * X) * p + (S — 48 * X) * p = 2000
S * (1 + 49 * p — 24 * p) = 2000
S * (1 + 25 * 0,01) = 2000
1,25 * S = 2000
S = 2000 / 1,25
S = 1600 тыс. руб., или 1,6 млн руб.
Ответ: 1,6 млн руб.
Задача 2. Рассчитать сумму кредита
15 декабря планируется взять кредит в банке на 21 месяц. Условия возврата таковы:
1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
cо 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
15-го числа каждого месяца с 1-го по 20-й долг должен быть на 30 тыс. руб. меньше долга на 15-е число предыдущего месяца;
к 15-му числу 21-го месяца кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1,604 млн руб. (1604 тыс. руб.)?
Решение:
Задача отличается от предыдущей — выплаты по основному долгу (30 тыс. руб.) осуществляются только первые 20 месяцев, а значит, в последний месяц выплата будет иной.
S тыс. руб. — сумма кредита
р = 0,03
Суммы ежемесячного долга: S; (S — 30); (S — 60... S — 570); (S — 600); 0
Начисленные проценты: S * р; (S — 30) * р; (S — 60) * р... (S — 570) * р; (S — 600) * р; 0
Сумма выплат = Сумма кредита + Проценты
S * (1 + 21 * 0,03) — 0,03 * 6300 = 1604
1,63 * S — 189 = 1604
1,63 * S = 1604 + 189
1,63 * S = 1793
S = 1793 / 1,63
S = 1100 тыс. руб., или 1,1 млн руб.
Ответ: 1,1 млн руб.
Задача 3. Рассчитать, на сколько месяцев планируется взять кредит
15 января планируется взять кредит в банке на некоторый срок (целое число месяцев). Условия его выплаты таковы:
1-го числа n-ого месяца долг возрастёт на 3% по сравнению с концом предыдущего месяца;
с 2-го по 14-е число n-ого месяца необходимо выплатить часть долга;
15-го числа k-того месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
На сколько месяцев планируется взять кредит, если известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит?
Решение:
Превышение выплат на 30% от суммы кредита — за счёт выплаченных процентов.
Следовательно,
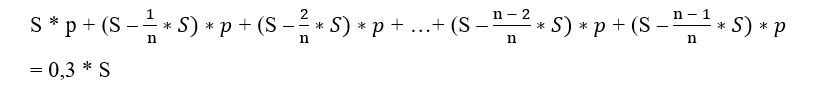
Раскрываем скобки и группируем слагаемые.
Ответ: 19 месяцев.
https://journal.open-broker.ru/ (C)
Не является индивидуальной инвестиционной рекомендацией
При копировании ссылка обязательна Нашли ошибку: выделить и нажать Ctrl+Enter
В этом случае мы имеем дело с дифференцированными платежами.
Внимание: в задачах этого типа применяется формула суммы n-первых членов арифметической прогрессии.
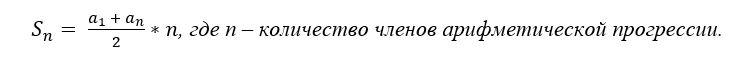
Задачи для разбора берутся из вариантов ЕГЭ прошлых лет, размещённых на популярном среди школьников и учителей сайте РЕШУ ЕГЭ.
Задача 1. Рассчитать сумму кредита
15 января планируется взять кредит в банке на 49 месяцев. Условия его возврата таковы:
1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
с 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Какую сумму следует взять в кредит, чтобы общая сумма выплат по кредиту после полного его погашения составила 2 млн руб. (никакие округления при вычислении платежей не производятся)?
Решение:
S тыс. руб. — сумма кредита,
р = 0,01,
2 млн руб. = 2000 тыс. руб.,
X тыс. руб. — ежемесячная выплата основного долга.
Суммы ежемесячного долга: S; (S — X); (S — 2 * X ... S — 47 * X); (S — 48 * X); 0
Начисленные проценты: S * p; (S — X) * p; (S — 2 * X) * p ... (S — 47 * X) * p; (S — 48 * X) * p; 0
Сумма выплат = Сумма кредита + Проценты
S + S * p + (S — X) * p + (S — 2 * X) * p + ...+ (S — 47 * X) * p + (S — 48 * X) * p = 2000
S * (1 + 49 * p — 24 * p) = 2000
S * (1 + 25 * 0,01) = 2000
1,25 * S = 2000
S = 2000 / 1,25
S = 1600 тыс. руб., или 1,6 млн руб.
Ответ: 1,6 млн руб.
Задача 2. Рассчитать сумму кредита
15 декабря планируется взять кредит в банке на 21 месяц. Условия возврата таковы:
1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
cо 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
15-го числа каждого месяца с 1-го по 20-й долг должен быть на 30 тыс. руб. меньше долга на 15-е число предыдущего месяца;
к 15-му числу 21-го месяца кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1,604 млн руб. (1604 тыс. руб.)?
Решение:
Задача отличается от предыдущей — выплаты по основному долгу (30 тыс. руб.) осуществляются только первые 20 месяцев, а значит, в последний месяц выплата будет иной.
S тыс. руб. — сумма кредита
р = 0,03
Суммы ежемесячного долга: S; (S — 30); (S — 60... S — 570); (S — 600); 0
Начисленные проценты: S * р; (S — 30) * р; (S — 60) * р... (S — 570) * р; (S — 600) * р; 0
Сумма выплат = Сумма кредита + Проценты
S * (1 + 21 * 0,03) — 0,03 * 6300 = 1604
1,63 * S — 189 = 1604
1,63 * S = 1604 + 189
1,63 * S = 1793
S = 1793 / 1,63
S = 1100 тыс. руб., или 1,1 млн руб.
Ответ: 1,1 млн руб.
Задача 3. Рассчитать, на сколько месяцев планируется взять кредит
15 января планируется взять кредит в банке на некоторый срок (целое число месяцев). Условия его выплаты таковы:
1-го числа n-ого месяца долг возрастёт на 3% по сравнению с концом предыдущего месяца;
с 2-го по 14-е число n-ого месяца необходимо выплатить часть долга;
15-го числа k-того месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
На сколько месяцев планируется взять кредит, если известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит?
Решение:
Превышение выплат на 30% от суммы кредита — за счёт выплаченных процентов.
Следовательно,
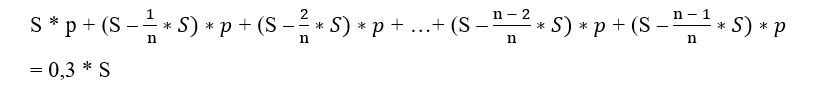
Раскрываем скобки и группируем слагаемые.
Ответ: 19 месяцев.
https://journal.open-broker.ru/ (C)
Не является индивидуальной инвестиционной рекомендацией
При копировании ссылка обязательна Нашли ошибку: выделить и нажать Ctrl+Enter