12 сентября 2011 Mind Money (ИК Церих) Подлевских Николай
Десять лет назад 11 сентября 2001 года было совершено нападение на башни Всемирного торгового центра. Событие сильно повлиявшее на ход мировой истории было большой неожиданностью для подавляющего числа жителей планеты. Течение событий никогда не было плавным. Однако сейчас роль турбулентностей и неожиданностей возросла как никогда. В этой связи полезно взглянуть на развивающиеся вокруг нас закономерности через призму редких событий, которые автор популярной книги «Черный лебедь. Под знаком непредсказуемости» Насим Талеб называет «черными лебедями»
Мы не знаем будущего. Точность прогнозов очень низка. Особенно остра эта проблема в экономике, где не удается прогнозировать начало экономических спадов, крахи на биржах, взлет новых компаний. Но острая нужда в прогнозах заставляет ими заниматься. Большинство экономистов и аналитиков с неохотой дают прогнозы, а те, кто решается на это редко оказываются правы. В оправдание низкой выполняемости прогнозов аналитиков можно сказать, что у них, как и у всех людей может быть свое «математическое ожидание» на любую изменяемую величину. Например, на курс доллара. Вот только потребителям важно помнить, что точность таких прогнозов, как правило, очень низкая.
Тем более, когда прогнозы делаются простыми методами экстраполяции. Но к большому сожалению, риски банков зачастую оцениваются как раз по простым схемам экстраполяции. Глядя на изменение цены актива риск менеджеры банка оценивают величину снижения их стоимости по величине среднеквадратичного отклонения, показанную в прошлом. Методы оценки рисков, оценки вероятности возможных потерь VaR являются основой риск менеджмента в современных финансовых учреждениях. Методики оценок VaR рекомендованы Базельским банковским комитетом состоят из нескольких простых этапов.
Общий портфель активов разбивается по видам активов и для каждого из них определяется величина возможных потерь VaR. И так по каждому активу входящему в портфель финансовой структуры. Для вычисления VaR необходимо определить ряд базовых элементов, влияющих на его величину. В первую очередь это оценки различных рисков. Наиболее важные из них – рыночные оцениваются по прошлой истории поведения данного актива. Так, если предположить, что логарифмы изменений цен активов подчиняются нормальному гауссову закону распределения с нулевым средним, то достаточно оценить только волатильность (т. е. стандартное отклонение). После задания распределения рыночных факторов необходимо выбрать доверительный уровень (confidence level), то есть вероятность, с которой потери не должны превышать VaR. В результате по выбранному активу можно формулировать предложения типа: С вероятностью Р потери за день не превысят величины VaR. Достаточно вычислить только однодневное VaR. (Обычно расчет VaR производится для доверительных уровней 90%, 95%, 97,5% и 99%). Показатель VaR для единицы стоимости финансового инструмента рассчитывается по формуле: VaR=К*sigm, где K - коэффициент, соответствующий каждому из доверительных уровней (90% - 1,28, 95% - 1,65, 97,5% -1,96 и 99% -2,33). Затем надо определить период поддержания позиций (holding period), на котором оцениваются потери. При упрощающих предположениях VaR пропорционален квадратному корню из периода поддержания позиций. Тогда, например, четырехдневное VaR будет в два раза больше однодневного. VaR на несколько дней определяется умножением однодневного VaR на квадратный корень их числа дней.
Но здесь вылезает самая главная погрешность. Среднеквадратичное отклонение sigm определяется из предположения, что отклонение цен является гауссовым. (На реальном рынке предположение о нормальности распределения, как правило, не выполняется). Затем ПРЕДПОЛАГАЕТСЯ, что в будущем распределение тоже будет нормальным и исходя из этого предположения определяется вероятность снижения стоимости актива на VaR. Основная ошибка таких оценок состоит в том, что реальная кривая распределения случайных величин может описываться самыми разными функциями. Выведенное для действия множества независимых факторов нормальное распределение дает существенные отклонения при описании поведения фондового рынка. Так, распределение дневного изменения цен на фондовом рынке имеет существенно более «тяжелые хвосты», чем это следует из гауссовой кривой нормального распределения. Так в реальности наблюдаются такие изменения цен, которых для нормального распределения приращений цен нужно было бы ждать миллионы лет. Такие сильные изменения индексов можно было наблюдать например в 2008 году, а так же в августе 2011 года. Еще более впечатляющие отклонения обвалы можно наблюдать не на такой длительной, но уже вполне интересной истории индекса РТС.
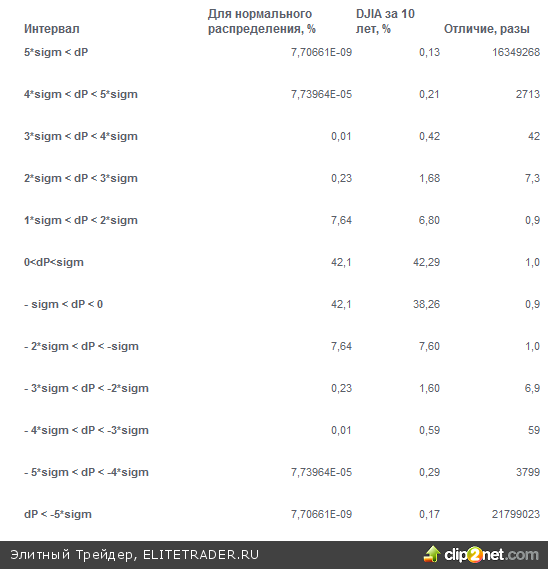
В приведенной ниже таблице представлены вероятности распределения случайной величины, распределенной по нормальному закону распределения в интервалы отклонений от среднего. Видим, что вероятность отклонения на величину более, чем 2*sigm составляет менее 1%, а вероятность отклонений больших 3* sigm быстро стремится к нулю. Так, для нормального распределения вероятность отклонения более, чем на 5sigm составляет 1,5/10000000000. Чтобы дождаться таких дневных отклонений требуется 10 млрд. дней или 27 млн. лет. А индекс Доу Джонса за десять лет показал 3 дня роста и 4 дня падений на величины большие 5 sigm. Из чего можно заключить, что сильные изменения рынка не могут описываться нормальным распределением, а вероятность больших дневных изменений цен может быть существенно больше, чем для гауссовой кривой.
В третьем столбце представлены частоты дневных отклонений индекса Доу Джонса за последние 10 лет. Видим, что, если для изменений в пределах 2*sigm отличия частоты от расчетной вероятности для нормального закона распределения не столь существенны, то по мере удаления от математического ожидания за пределы нескольких стандартных отклонений различия становятся слишком разительными. (Небольшая несимметрия реальной функции распределения логарифма отношений цен отражает неэквивалентность роста и падения рынка на долгосрочном периоде).
Аналогично наблюдаются довольно существенные отклонения вероятности больших изменений за несколько дней (растут не пропорционально квадратному корню из числа дней). Например, для вероятности большого снижения в периоды затяжного многодневного падения мы можем получить сильные отклонения от законов нормального распределения.
Как правило, сильные изменения, выбивающиеся из законов нормального распределения связаны с редкими, но принципиальными событиями. Вот так оценивает финансовые угрозы Насим Талеб: «Глобализация создала взаимосвязанную хрупкость, уменьшив волатильность и создав видимость стабильности. Иными словами, она создаёт Чёрных Лебедей. Мы никогда раньше не жили под угрозой глобального коллапса. Финансовые учреждения сливаются во всё меньшее число очень больших банков. Все банки взаимосвязаны. Финансовая биосфера поедается гигантскими, кровосмесительными, бюрократическими банками, и когда один из них упадёт, упадут все. Увеличивающаяся концентрация капитала в банковской среде кажется делающей финансовые кризисы менее вероятными, но когда они всё же случаются, они становятся более глобальными и наносят по нам более сильный удар. Мы перешли от диверсифицированной «биосферы» малых банков с разнообразной политикой предоставления кредитов, к более однородной среде фирм, где одна напоминает другую. Действительно, мы сейчас имеем меньше случаев банкротств, но когда они случатся… я боюсь даже подумать об этом».
Участникам рынков остается отслеживать развитие событий, ожидать новых волн количественного смягчения от ценробанков и выбирать оптимальную линию поведения из имеющейся у них информации о складывающихся трендах. Полагаю, что в условиях сильной турбулентности полезно чаще отрывать взгляд от своих повседневных занятий и пытаться более широко взглянуть на происходящее вокруг
Мы не знаем будущего. Точность прогнозов очень низка. Особенно остра эта проблема в экономике, где не удается прогнозировать начало экономических спадов, крахи на биржах, взлет новых компаний. Но острая нужда в прогнозах заставляет ими заниматься. Большинство экономистов и аналитиков с неохотой дают прогнозы, а те, кто решается на это редко оказываются правы. В оправдание низкой выполняемости прогнозов аналитиков можно сказать, что у них, как и у всех людей может быть свое «математическое ожидание» на любую изменяемую величину. Например, на курс доллара. Вот только потребителям важно помнить, что точность таких прогнозов, как правило, очень низкая.
Тем более, когда прогнозы делаются простыми методами экстраполяции. Но к большому сожалению, риски банков зачастую оцениваются как раз по простым схемам экстраполяции. Глядя на изменение цены актива риск менеджеры банка оценивают величину снижения их стоимости по величине среднеквадратичного отклонения, показанную в прошлом. Методы оценки рисков, оценки вероятности возможных потерь VaR являются основой риск менеджмента в современных финансовых учреждениях. Методики оценок VaR рекомендованы Базельским банковским комитетом состоят из нескольких простых этапов.
Общий портфель активов разбивается по видам активов и для каждого из них определяется величина возможных потерь VaR. И так по каждому активу входящему в портфель финансовой структуры. Для вычисления VaR необходимо определить ряд базовых элементов, влияющих на его величину. В первую очередь это оценки различных рисков. Наиболее важные из них – рыночные оцениваются по прошлой истории поведения данного актива. Так, если предположить, что логарифмы изменений цен активов подчиняются нормальному гауссову закону распределения с нулевым средним, то достаточно оценить только волатильность (т. е. стандартное отклонение). После задания распределения рыночных факторов необходимо выбрать доверительный уровень (confidence level), то есть вероятность, с которой потери не должны превышать VaR. В результате по выбранному активу можно формулировать предложения типа: С вероятностью Р потери за день не превысят величины VaR. Достаточно вычислить только однодневное VaR. (Обычно расчет VaR производится для доверительных уровней 90%, 95%, 97,5% и 99%). Показатель VaR для единицы стоимости финансового инструмента рассчитывается по формуле: VaR=К*sigm, где K - коэффициент, соответствующий каждому из доверительных уровней (90% - 1,28, 95% - 1,65, 97,5% -1,96 и 99% -2,33). Затем надо определить период поддержания позиций (holding period), на котором оцениваются потери. При упрощающих предположениях VaR пропорционален квадратному корню из периода поддержания позиций. Тогда, например, четырехдневное VaR будет в два раза больше однодневного. VaR на несколько дней определяется умножением однодневного VaR на квадратный корень их числа дней.
Но здесь вылезает самая главная погрешность. Среднеквадратичное отклонение sigm определяется из предположения, что отклонение цен является гауссовым. (На реальном рынке предположение о нормальности распределения, как правило, не выполняется). Затем ПРЕДПОЛАГАЕТСЯ, что в будущем распределение тоже будет нормальным и исходя из этого предположения определяется вероятность снижения стоимости актива на VaR. Основная ошибка таких оценок состоит в том, что реальная кривая распределения случайных величин может описываться самыми разными функциями. Выведенное для действия множества независимых факторов нормальное распределение дает существенные отклонения при описании поведения фондового рынка. Так, распределение дневного изменения цен на фондовом рынке имеет существенно более «тяжелые хвосты», чем это следует из гауссовой кривой нормального распределения. Так в реальности наблюдаются такие изменения цен, которых для нормального распределения приращений цен нужно было бы ждать миллионы лет. Такие сильные изменения индексов можно было наблюдать например в 2008 году, а так же в августе 2011 года. Еще более впечатляющие отклонения обвалы можно наблюдать не на такой длительной, но уже вполне интересной истории индекса РТС.
В приведенной ниже таблице представлены вероятности распределения случайной величины, распределенной по нормальному закону распределения в интервалы отклонений от среднего. Видим, что вероятность отклонения на величину более, чем 2*sigm составляет менее 1%, а вероятность отклонений больших 3* sigm быстро стремится к нулю. Так, для нормального распределения вероятность отклонения более, чем на 5sigm составляет 1,5/10000000000. Чтобы дождаться таких дневных отклонений требуется 10 млрд. дней или 27 млн. лет. А индекс Доу Джонса за десять лет показал 3 дня роста и 4 дня падений на величины большие 5 sigm. Из чего можно заключить, что сильные изменения рынка не могут описываться нормальным распределением, а вероятность больших дневных изменений цен может быть существенно больше, чем для гауссовой кривой.
В третьем столбце представлены частоты дневных отклонений индекса Доу Джонса за последние 10 лет. Видим, что, если для изменений в пределах 2*sigm отличия частоты от расчетной вероятности для нормального закона распределения не столь существенны, то по мере удаления от математического ожидания за пределы нескольких стандартных отклонений различия становятся слишком разительными. (Небольшая несимметрия реальной функции распределения логарифма отношений цен отражает неэквивалентность роста и падения рынка на долгосрочном периоде).
Аналогично наблюдаются довольно существенные отклонения вероятности больших изменений за несколько дней (растут не пропорционально квадратному корню из числа дней). Например, для вероятности большого снижения в периоды затяжного многодневного падения мы можем получить сильные отклонения от законов нормального распределения.
Как правило, сильные изменения, выбивающиеся из законов нормального распределения связаны с редкими, но принципиальными событиями. Вот так оценивает финансовые угрозы Насим Талеб: «Глобализация создала взаимосвязанную хрупкость, уменьшив волатильность и создав видимость стабильности. Иными словами, она создаёт Чёрных Лебедей. Мы никогда раньше не жили под угрозой глобального коллапса. Финансовые учреждения сливаются во всё меньшее число очень больших банков. Все банки взаимосвязаны. Финансовая биосфера поедается гигантскими, кровосмесительными, бюрократическими банками, и когда один из них упадёт, упадут все. Увеличивающаяся концентрация капитала в банковской среде кажется делающей финансовые кризисы менее вероятными, но когда они всё же случаются, они становятся более глобальными и наносят по нам более сильный удар. Мы перешли от диверсифицированной «биосферы» малых банков с разнообразной политикой предоставления кредитов, к более однородной среде фирм, где одна напоминает другую. Действительно, мы сейчас имеем меньше случаев банкротств, но когда они случатся… я боюсь даже подумать об этом».
Участникам рынков остается отслеживать развитие событий, ожидать новых волн количественного смягчения от ценробанков и выбирать оптимальную линию поведения из имеющейся у них информации о складывающихся трендах. Полагаю, что в условиях сильной турбулентности полезно чаще отрывать взгляд от своих повседневных занятий и пытаться более широко взглянуть на происходящее вокруг
/Элитный Трейдер, ELITETRADER.RU/
https://mind-money.eu Источник
Не является индивидуальной инвестиционной рекомендацией | При копировании ссылка обязательна | Нашли ошибку - выделить и нажать Ctrl+Enter | Жалоба