8 января 2014 Подлевских Николай
1. Коэффициент корреляции это лишь одна характеристика из множества параметров и не нужно переоценивать его значения
Приходящие с биржевых терминалов потоки ценовой информации указывают на наличие как хаотичного случайного компонента в поведении цен, так и неко- торой их согласованности с ценами других активов. Математическая статистика позволяет выявить эле- менты связности поведения временных рядов. Для этого можно проводить анализ Фурье или оценивать другие параметры. Наиболее удобным и простым является коэффициент регрессии (корреляции) К. Он часто используется для анализа степени связанности двух временных рядов. Этот коэффициент может быть определен для любых двух совокупностей (в том числе случайных) величин Xi и Yi, где i пробега- ет значения от 1 до n. По выборке длиной n можно определить эмпирической коэффициент корреляции, который определяется по следующей формуле:
K= , где Mx и Му – оценки математического ожидания случайных ве- личин {X} и {Y}, а – величины их среднеквадратичных отклонений. К изменяется в пределах (-1, 1).
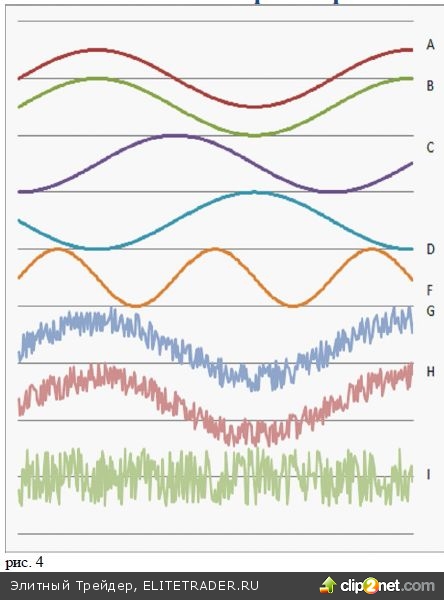
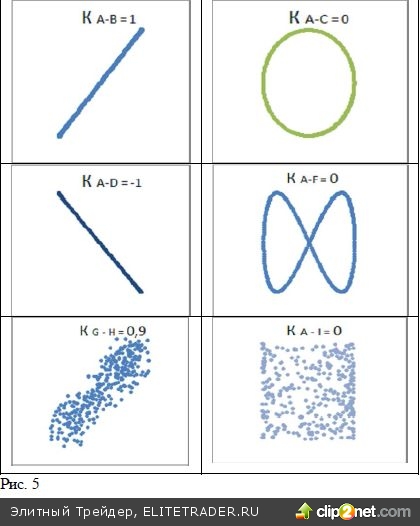
Коэффициент корреляции оказывается равным едини- це для наборов двух величин X(ti) и Y(ti), значения которых синфазно изменяются со временем, таких как обозначенные буквами А и В синусоиды на рисунке 4. На серии рисунков 5 эти наборы зависимостей X(ti) и Y(ti) представлены в координатах (Х и У). Для проти- вофазных колебаний (кривые А и D) коэффициент корреляции равен -1. При смещении фазы одного из процессов коэффициент корреляции уменьшается, чтобы стать близким к нулю для ортогональных коле- баний sin(t) и cos(t) (кривые А и C). Аналогично, нулевую корреляцию обнаружим у колебаний с отли- чающимися в два раза периодами колебаний sin(t) sin(2t) (Кривые А и F). Коэффициент корреляции уменьшается и за счет «зашумления» колебаний двух разных процессов. Так, для синхронно колеблющихся кривых G и H, в которых имеется случайный шум, рассчитанный коэффициент корреляции оказывается уже меньшим единицы. Чаще именно подобное зашумленное поведение наблюдается для цен различных активов. Корреляция набора чисто случайных чисел Yi с любой зависимостью X(ti) будет стремиться к нулю по мере роста выборки, а «график» пар чисел X(ti) и Yi не будет давать даже намеков на зависимость, как это изображено на последнем графике для «зависимости» пар чисел Xi и Yi, где Xi бралось с верхней синусоидальной кривой А, а Yi считывалось с кривой I, представляющей собой набор равномерно распределенных случайных чисел.
2. Следует помнить о возможной точности определения корреляции
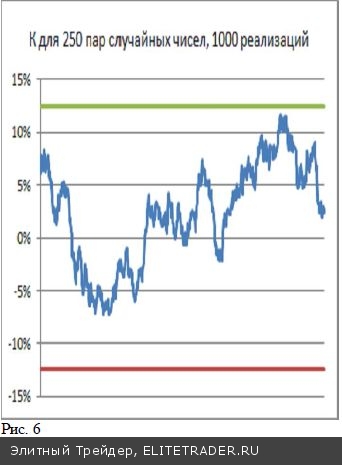
В рыночных зависимостях кроме детерминированных компо- нент, которые приводят к часто наблюдаемой связанности их поведения, присутствуют также другие слагаемые, которые можно трактовать как «число случайные». Случайные слагае- мые тоже дают вклад в определяемый коэффициент корреляции К. Так, при расчете К для конечной выборки раз- мером N между двумя наборами Xi и Yi случайных величин, равномерно распределенных на интервале (0-1), тоже будут получаться отличные от нуля значения. Значение Кj(250) (для выборки размером 250 пар) будет зависеть от номера j самой выборки. Коэффициент корреляции К будет случайной вели- чиной, реализации которого Kj согласно закону больших чисел оказываются распределенными по нормальному закону. На представленном рисунке видим, как изменялись коэффициен- ты корреляций Кj(250) между выборками по 250 пар случайных величин для тысячи реализаций (j=1,2,3…1000). Среднеквадратичное отклонение ?? случайной величины К (250) близко к 0,062, а значит, что в 77% случаев эмпирическое значение коэффициента корреляции Кj(250) для 250 пар случайных величин будет находиться в пределах ±2??. (Ли- нии ±0,124 приведены на рисунке). А за пределы 3*?? (±0,186) случайная величина Кj(250) будет выходить только в 1,35% случаев. Таким образом, значе- ние К(250) для набора 250 пар чисел, большее по модулю 0,2, скорее всего, не может быть связанным со случайными обстоятельствами, и для временных рядов с К>0,2 приходится отбрасывать идею об их случайном изменении и можно ис- кать возможные причины их коррелированного поведения. Для нормально распределения Kj(N) величина ?? обратно пропорциональна квадратному корню из размера выборки N. Поэтому для выборки размером в 1000 пар случайных чисел ?? уменьшится в два раза по сравнению с выборкой из 250 пар случайных чисел, а выборки меньшей в четыре раза, размером в 62 пары точек ??, напротив, вырастет в два раза. Если считать, что в цене акций имеется заданный детерминированный компонент и случайное слагаемое, то увеличивая объем выборки можно уменьшить добавку в коэффициент корреляции, которая возникает за счет случайного слагаемого. В случае временного ряда, для сниже- ния вклада случайных компонентов нужно увеличивать период, с которого берутся используемые точки. Однако слишком увеличивать период исследования тоже нельзя, поскольку на большом интервале вполне может изменяться характер согласованности кривых. Понятно, что с помощью коэффициента корреляции оценивается только среднее значение корреляции за период. Поэтому в качестве окна изучения чаще всего используют годовой интервал, дающий с учетом выходных и праздничных нера- бочих дней около 250 дневных цен закрытия. Выбирая годовой интервал, следует помнить, что в полученном коэффициенте корреляции К(250) могут давать вклад случайные компоненты цены, величина которого на выборке в 250 точек легко может составлять ±0,1, а в отдельных (пусть и редких) случаях дос- тигать даже ±0,2. Поэтому реально при вычислении коэффициента корреляции на годовом интервале есть смысл удерживать только одну значащую цифру по- сле запятой, а все остальное может быть связано со статистическими погрешностями. Если же коэффициент корреляции К(250) оказывается меньшим 10%, то о взаимосвязи исходных величин лучше не думать. (Нет смысла искать неслучайных вещей там, где доминирует случайность).
3. Корреляции индексов
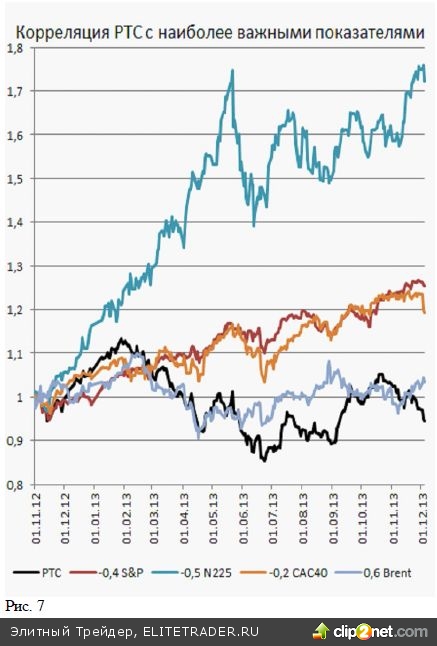
С учетом приведенной выше оценки точности можно рассчитать коэффициенты корреляции потенциально наиболее значимых для индекса РТС величин. На приведенном рисунке изображены относительные изменения индекса РТС, американского индекса S&P 500, японского Nikkei225 и французского CAC40. Оказывается, что в последний год коэффициент кор- реляции индекса РТС с указанными индексами составлял отрицательную величину. (Значения К для РТС с указанными выше индексами приведены в подписях к кривым на рисунке). Отрицательной величина корреляции становится за счет длительных периодов разнонаправленных движений индексов. Так, индекс РТС в первой половине года снижался, в то время как индексы указанных стран показывали рост. Особенно сильно подрос индекс N225, что и дало высокий отрицательный коэффициент К. По- ложительным коэффициент корреляции (из приведенных кривых) оказался только для цен нефти марки Brent. Хотя коэффициент К с нефтью +0,6 оказывается не столь высоким, как это можно было бы предположить, с учетом зависимости нашей эко- номики от цен на это сырье.
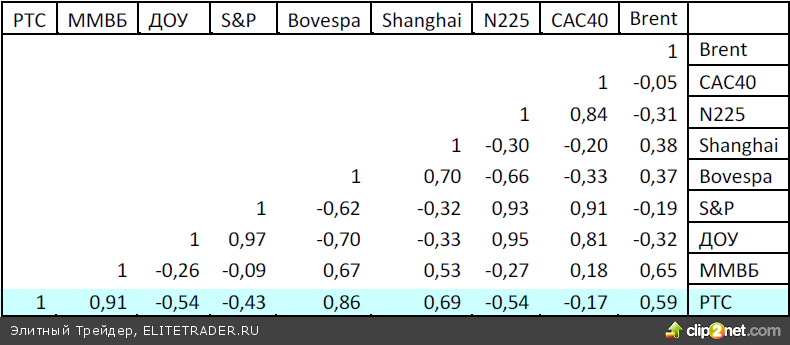
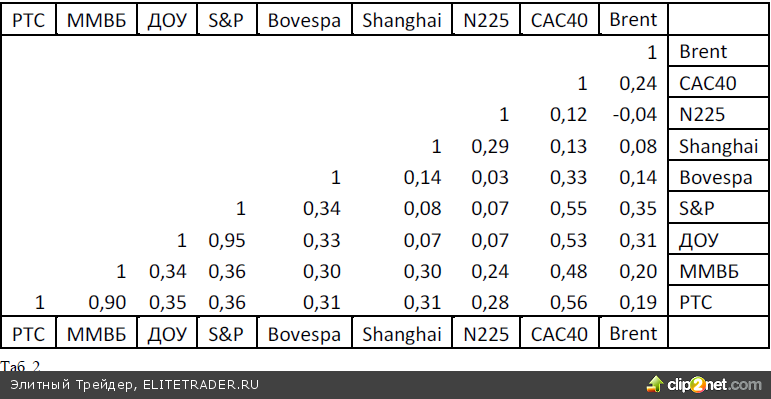
Из приведенной Таблицы 1 попарных корреляций видим, что указанные активы распределяются на две группы. В одной располагаются индексы развитых стран, которые имеют между собой достаточно высокие положительные значения по- парной корреляции. Так, коэффициент корреляции индекса S&P 500 и индекса САС 40 очень высок и составляет +0,9. В то время как коэффициенты корреля- ции с индексами стран BRICS для них оказываются отрицательными.
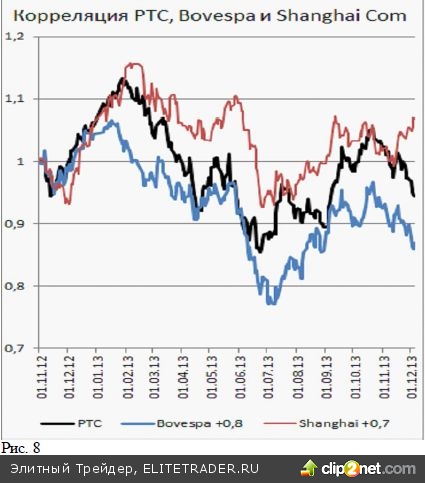
В другую группу выделяются индексы стран BRICS. На совместном графике относительных изменений индексов хорошо видно их согласованное поведение. Коэффициент корреляции РТС с индексами Китая и Бразилии оказывается даже чуть большим, чем зави- симость индекса РТС от цен нефти. Это указывает на достаточно высокую связанность поведения индексов стран BRICS. Из приведенных на двух рисунках кривых и коэффи- циентов корреляции этих кривых с индексом РТС можно сделать предположение, что на годовом гори- зонте решение об инвестировании в фондовый рынок России, Бразилии и Китая набором основных инве- сторов, определявших динамику индексов, принимались по схожим соображениям. Аналогично, как и решения об инвестировании в рынки США, Японии и Франции.
4. Корреляции приращений цен
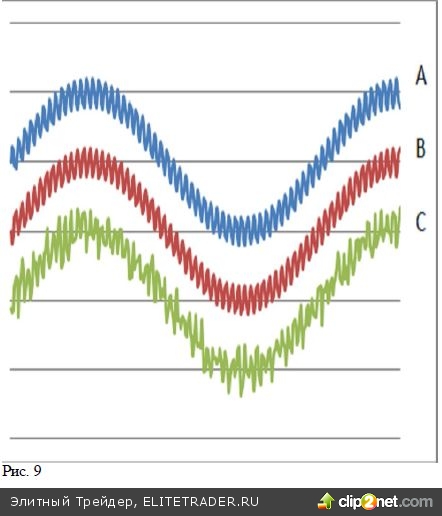
Важно обратить внимание еще на одну важную осо- бенность. Для спекулянта гораздо большее значение имеет не корреляция цен акций, но корреляция днев- ных изменений цен. А это совсем не одно и то же. На рисунке 9. представлены три модельных графика. Каждый из них представляет сумму длиннопериод- ной синусоиды (годовые изменения) с соответствующей добавкой. А вот добавка для трех графиков разная. Для графика А - это «недельная» синусоида с периодом в 5 дней. Для графика В и С – недельная синусоида имеет отрицательный знак, так что на графиках А она находится в противофазе с добавкой на графиках В и С. На графике С, кроме того, имеется случайная добавка. Амплитуды всех добавок выбраны равной пятой части амплитуды основного колебания. Попарные коэффициенты кор- реляции кривых, несмотря на добавки, близки к единице и равны КА-В=+0,92; КА-С=+0,9; КB-С= + 0,9.
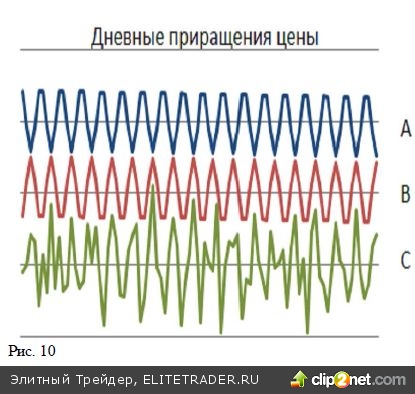
А вот для «дневных приращений цены», приведенных на втором графике картина, совсем иная. Точки на кривых А, В, С на рис. 10 получены в результате вычисления разностей последовательных по времени значений на кривых рис.9: Арис.10=Арис.9(t)-A рис.9(t-?t). Как видим, дневные приращения цен гораздо меньше зависят от годовых трендов, но в большей мере опре- деляются короткими колебаниями, имеющими период в несколько дней. Для указанных разностных кривых (рис.10) коэффициенты корреляции имеют совсем другие значения КА-В= -1,0; КА-С= -0,7; КB-С= + 0,7. Коэффициенты корреляции вычислены по вы- боркам в 250 пар. (С учетом предыдущего пункта ограничиваемся одним знаком после запятой для кривых содержащих случайную компоненту).
Аналогично можно поступить с использовавшимися выше индексами и обра- зовать из них наборы дневных приращений. Для полученных рядов относительных приращений были рассчитаны значения коэффициентов кор- реляции. Как видим из приведенной ниже таблицы 2, значения коэффициентов корреляции принципиально отличаются от соответствующих величин, приведенных в таблице 1.
Главное отличие состоит в большей устойчивости таких коэффициентов. Кроме того, корреляции приращений в основном оказываются положитель- ными. Исключением оказалось отрицательная величина корреляции приращений цены нефти и приращений японского индекса Nikkei 225. Однако абсолютные значения коэффициентов корреляции для приращений оказыва- ются, как правило, заметно меньшими, чем для самих величин и, в большинстве случаев, лишь немногим превышают возможные значения для наборов чисто случайных величин.
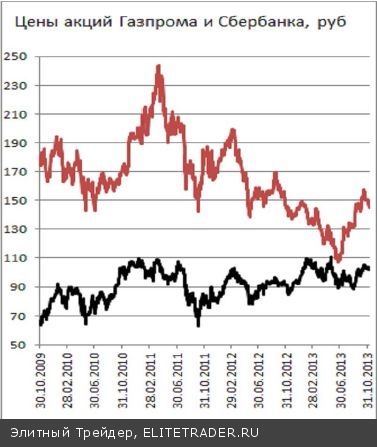
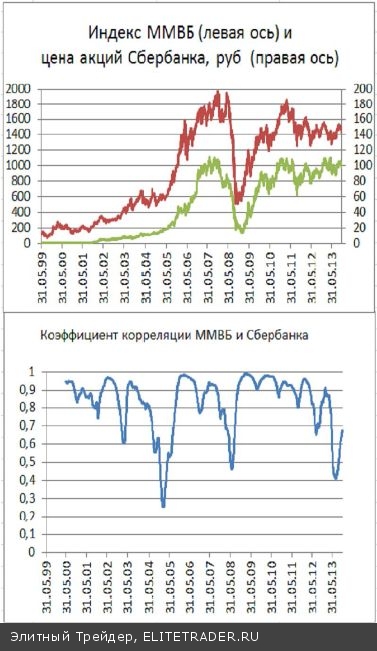
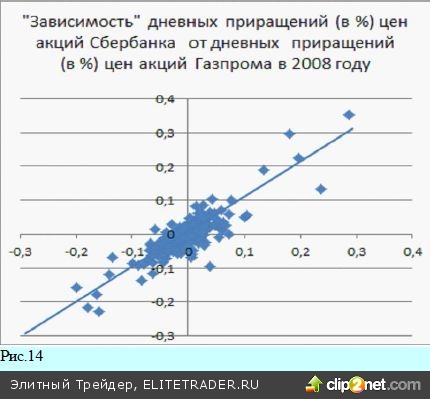
Степень устойчивости коэффициента корреляции можно продемонстрировать на их временных зави- симостях. Как уже упоминалось, коэффициент корреляции зависит от времени. Так, для двух наибо- лее ликвидных бумаг российского рынка, цен акций Сбербанка и Газпрома коэффициент корреляции (вычисленный по предыдущим 250 дням - пример- ный годовой интервал) сильно изменяется со временем. Например, в конце 2008 года коэффициент корреляции приближался к +1. Значит, в 2008 году в динамике цен акций преобладала согласованная ком- понента. Однако были периоды, когда коэффициент корреля- ции опускался в отрицательную область. Значит, в течение года, предшествовавшего таким провалам, значений корреляции, цены акций Газпрома и Сбер- банка изменялись в большей мере разнонаправленно. Такого рода разнонаправленность является довольно частым явлением на нашем рынке. Так часто проти- вофазное рынку движение показывали акции Сургутнефтегаза, Норильского Никеля или некото- рые другие акции. Это происходило либо по специфическим корпоративным причинам, либо, когда инвесторы на рынке выбирали какие-либо ак- ции в качестве защитного актива. А вот краткосрочные изменения цен акций, пусть даже в среднем, не являются столь высоко согласо- ванными, но зато демонстрируют большую устойчивость коэффициента корреляции в разные периоды времени. Такое отличие можно увидеть, сопоставляя поведение корреляции как самих цен акций Сбербанка и Газпрома (рис. 12), так и их изме- нений (рис.13). Рис.14 Стоит отметить, что даже для периодов высокой корреляции «зависимость» приращений цен одних акций от приращения цен других акций выглядит совсем не как динамическая кривая. Тем не менее, при больших К с достаточно большой вероятностью будет работать линейная регрессионная зависимость. В результате, можно, например, по приращению цен акций Газпрома оценить приращение акций Сбербан- ка (и наоборот). Однако беда такой зависимости состоит в том, что приращения цен указанных акций происходят за один временной интервал. И оценка вероятности приращения цены акций Сбербанка в определенный день возможна только при завершении этого же дня для акций Газпрома.
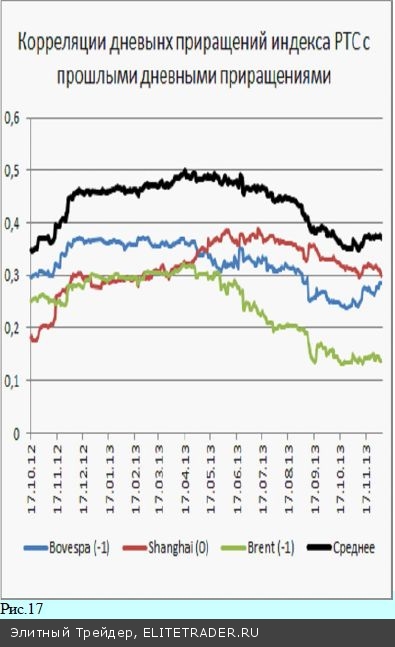
Определение коэффициентов корреляции между различными рядами данных позволяет быстро выявить наиболее простые зависимости и найти активы, ко- торые коррелируют с изучаемым. Так, по изменениям индексов зарубежных рынков или цен на товарные группы можно делать оценки вероятности теку- щих изменений индексов на нашем рынке. Но вот с самым главным – возможностью делать вероятностные прогнозы по уже произошедшим событиям все немного хуже. А ведь именно такого рода прогнозы имеют наибольшую ценность. Для этого нужно изучать корреляции сегодняшних приращений индекса с прошлыми приращениями индексов дру- гих рынков или приращениями цен товарных групп. Но по факту оказывается, что информация о прошлом довольно быстро девальвирует со временем. Из- вестная «максима» технического анализа «история цен содержат всю информацию о рынке», работает с большой натяжкой и при условии учета про- исходящих on-line событий. Реально прошлые цены определяют будущую динамику лишь в ограниченной мере. Для определения того, какое прошлое наиболее существенным образом влияет на настоящее, для начального анализа можно пытаться выстраивать корреля- цию текущих приращений с изменениями значений индексов, цен акций в предыдущие моменты времени. По факту оказывается, что уровни корреляции приращений из разных временных интервалов, как правило, имеют довольно низкие значения.
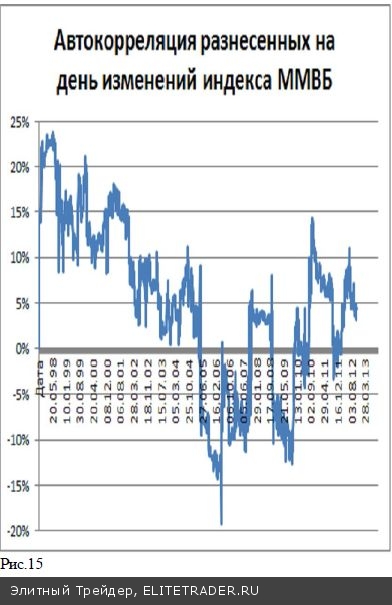
Это можно проиллюстрировать на примере автокорреля- ционной функции приращений индекса ММВБ. Корреляция берется для двух последовательных рядов дневных изменений индекса ММВБ. И если в качестве значений Xi берется дневное приращение индекса ММВБ за текущий день, то в качестве Yi выступают приращения индекса за предыдущий день. Из приведенного на рисунке 15 графика видим, что, во- первых, величина автокорреляции не сильно превышает значения коэффициента корреляции для пар чисто слу- чайных чисел. Во-вторых, К может изменять знак. И все же в длительные периоды знаковой определенно- сти коэффициента корреляции, с его использованием можно заработать на рынке деньги. Для этого, при поло- жительных К, достаточно покупать индекс под занавес торгов в дни, когда он закрывается с положительным приращением, и продавать в дни, когда индекс имеет отрицательное приращение. В результате, на периоде положительной определенности К можно получить ста- тистически значимое положительное приращение счета. В периоды отрицательного К, работоспособной будет контр трендовая к изменениям прошедшего дня методика.
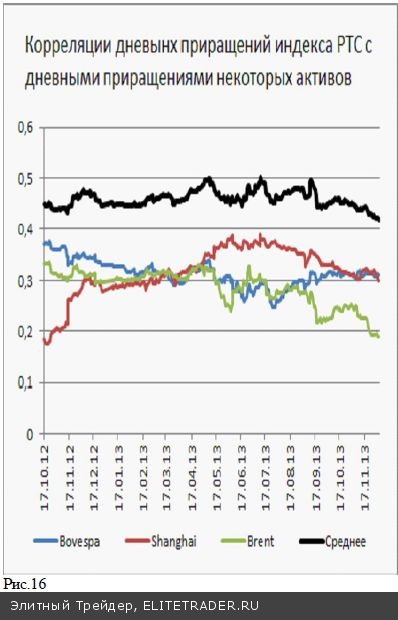
В заключение отметим, что из рядов данных, имеющих наибольшую корреляцию с изучаемым активом, можно отобрать наборы, имеющие наибольшие по модулю ко- эффициенты корреляции. Тогда, (взвешивая, например, пропорционально величине К) можно строить синтетиче- ские активы, которые будут потенциально иметь более глубокую связь с интересующим нас активом, и иметь большее значение коэффициента корреляции. На рис. 16 приведены рассчитанные за предыдущий прошедший год коэффициенты корреляции приращений индекса РТС к приращениям индекса Bovespa, Shanghai Com., цен нефти марки Brent. Видим, что все три указанных коэффициен- та в течение последнего года изменялись в окрестности значений 0,3. Образовав гипотетический актив, изменения которого равны среднему значению изменений трех указанных величин, так же можно рассчитать коэффициент корре- ляции для дневных приращений полученного актива. Рассчитанные по тем же правилам значения коэффици- ента корреляции приращений индекса РТС и указанного синтетического актива приведены на рис. 16 жирной линией. Видим, что уровни корреляции вновь образован- ного актива оказались систематически большими, чем для входящих в него слагаемых. На таком пути можно образовывать другие активы добиваясь получения более высоких значений коэффициентов корреляции. Наиболее очевидное практическое значение имеет ком- бинирование таких синтетических активов из уже ушедших в историю рядов данных. Так, в пару к Xi - изменениям индекса РТС можно, например, составить актив Yi из трех величин: изменений цен нефти и индек- са Bovespa в предыдущий день и значения индекса Shanghai Сomp., но уже в текущий торговый день, кото- рый в Китае заканчивается намного раньше, чем закрываются торги в Москве. Как и в предыдущем слу- чае, коэффициент корреляции приращений индекса РТС с такой синтетической переменной оказывается выше попарных корреляций с каждой из этих величин по от- дельности. Тем самым коэффициент корреляции помогает найти более тесно связанную с изменениями индекса РТС переменную, значения которой появляются раньше по времени, чем время закрытия индекса РТС. Поступая аналогичным образом можно отбирать наборы таких переменных, выбирая из них наиболее связанную пару с интересующим активом.
(Нужно быть готовым к кропотливой работе по предварительной очистке данных, учету праздничных дней, торговле в выходные дни, как это проис- ходит по нефти марки Brent и т.д.). И еще: правильнее брать не среднее значение входящих величин, а их взвешенные значения по средней величине коэффициента корреляции. Лучше ввести изменяемые параметры, подбирая которые можно добиться лучших результатов. Однако оптимизацию лучше проводить уже не по величине коэффициента корреляции, а по потенциаль- ной прибыли, которую можно получить, используя ту или иную торговую методику. Можно уже на этапе подбора исходных данных использовать нейросети, когда оптимизирующая система на этапе обучения сама подбира- ет наиболее подходящие коэффициенты. Но все это уже скорей относится к созданию торговой системы. В данном же тексте продемонстрировано то, как можно использовать коэффициенты корреляции.
РЕЗЮМЕ
Определение коэффициентов корреляции позволяет установить степень связанности изу- чаемых временных рядов. Большие значения коэффициентов корреляции свидетельствуют о высокой коррелированности поведения двух активов. Коэффициент корреляции К изме- няется со временем, но, к сожалению, определение К на малых интервалах может давать большие случайные отклонения. Поэтому реально приходится рассчитывать средние значе- ния К по временному интервалу. Для наборов дневных данных наиболее оптимальным для определений К является годовой интервал. Коэффициент корреляции позволяет проводить регрессионные прямые, которые в некото- рых случаях позволяют прогнозировать вероятность изменения интересующего актива по изменениям других активов. Особенно интересным это становится в случаях, когда можно получить значимые коэффициенты корреляции с рядами данных, которые для текущего момента уже стали историей. Для этого бывает полезным образование «синтетических акти- вов». Таким образом, коэффициент корреляции может быть полезным элементом предваритель- ного анализа исходных рядов цен, которые будут служить исходными данными для будущей торговой системы.
Не является индивидуальной инвестиционной рекомендацией | При копировании ссылка обязательна | Нашли ошибку - выделить и нажать Ctrl+Enter | Жалоба