10 августа 2015 QuantAlgos
Итак, по результатам голосования в лидерах оказалась публикация Alvaro Cartea и Sebastian Jaimungal "Algorithmic Trading of Co-integrated Assets". Я тоже считаю эту работу очень интересной, так как она фактически расширяет понятие парного трейдинга до торговли произвольным количеством активов, с учетом их коинтеграционного взаимоотношения. Это сильно повышает устойчивость результирующего портфеля, в отличие от парного трейдинга, в связи с его диверсификацией.
Представляю здесь перевод этой статьи, которую я несколько сократил, убрав длинные математические выкладки и оставив только наиболее важные и окончательные формулировки. Думаю, это значительно облегчит понимание, без утраты основного смысла публикации.
Вступление
Успех многих торговых алгоритмов зависит от качества предсказаний движения цены актива. Предсказания цены отдельной акции в общем случае менее точно, чем предсказание значения портфеля активов. Классической стратегией, которая использует совместное поведение двух активов, является парный трейдинг, где портфель состоит из линейной комбинации этих активов. Для примера, это могут быть две акции, чей спред, представляющий собой разницу их цен, демонстрирует особый паттерн, отклонения от которого носят временный характер. Алгоритм парного трейдинга получает прибыль от ставки на тот факт, что отклонения спреда возвратятся к их историческому или предсказуемому уровню.
В данной работе мы создадим оптимальную стратегию, в которой агент открывает позиции в n коинтегрированных активах. Цель стратегии - получение прибыли от структурной зависимости в динамике их цен . Мы предполагаем, что активы коинтегрированы и создадим алгоритмическую торговую стратегию, где инвестор максимизирует ожидаемую функцию владения ( то есть вложенные и наличные средства). Мы выведем отдельную закрытую формулу для оптимальной (динамической) инвестиционной стратегии и покажем, что она учитывает коинтеграционный фактор. Далее, мы используем данные торгов с биржи Nasdaq для калибровки модели и проведем симуляцию, чтобы продемонстрировать, насколько стратегия производительна, в случае, когда инвестор открывает позиции в трех активах : Google, Facebook и Amazon.
Мы предполагаем, что дрифт в приращениях цен активов состоит из компонента, присущего только данному активу, и общего компонента для всех используемых активов. Общий компонент, который мы называем краткосрочной альфа, представляет собой процесс возврата к среднему с нулевым средним, являющийся естественным источником прибыли в торговой стратегии - он определяет прибыль от краткосрочных инвестиционных возможностей для коллекции активов.
Коинтегрированные логарифмы цен с краткосрочной альфа
Предположим, что дрифт в приращениях цен активов состоит из особого и общего компонентов. Особый компонент есть результат факторов, влияющих только на каждый отдельный актив, и общий компонент - результат индустриального или секторального набора факторов, которые влияют на всю коллекцию используемых активов. Таким образом, у нас есть коллекция активов, чей вектор цен обозначим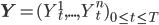 , который удовлетворяет системе дифференциальных уравнений:
, который удовлетворяет системе дифференциальных уравнений:
\begin{equation}\frac{dY_t^k}{Y_t^k}=(\nu_k+\delta_k\alpha_t)dt+\sum_{i=1}^n\sigma_{ki}dW_t^i\end{equation}
где особый компонент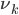 является константой, и общий компонент :
является константой, и общий компонент :
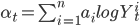
где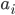 - константы, и
- константы, и 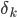 - специальная константа , которая показывает, как общий компонент влияет на каждый актив.
- специальная константа , которая показывает, как общий компонент влияет на каждый актив.
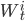 - стандартные Броуновские движения, независящие друг от друга, собранные в вектор
- стандартные Броуновские движения, независящие друг от друга, собранные в вектор 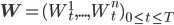 , и
, и 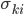 - неотрицательные константы. Мгновенную ковариацию между активами i и j можно определить как:
- неотрицательные константы. Мгновенную ковариацию между активами i и j можно определить как:
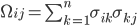 .
.
Далее, обозначим матрицу, чьими элементами являются
матрицу, чьими элементами являются 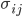 , представляющую собой разложение Холецкого мгновенной дисперсионно-ковариационной матрицы
, представляющую собой разложение Холецкого мгновенной дисперсионно-ковариационной матрицы 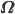 , таким образом
, таким образом 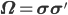 , где ' обозначает оператор транспонирования. Предположим, что нет дополнительных степеней свободы, так что
, где ' обозначает оператор транспонирования. Предположим, что нет дополнительных степеней свободы, так что  является обратимой.
является обратимой.
Покажем, что ведет себя как фактор коинтеграции. Когда
ведет себя как фактор коинтеграции. Когда 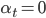 все активы являются геометрическими броуновскими движениями с дрифтом
все активы являются геометрическими броуновскими движениями с дрифтом 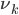 . В общем случае, на рынках акций,
. В общем случае, на рынках акций,  будет ненулевой и отклонения от ее долгосрочного или предсказуемого уровня быстро нивелируются. Такое поведение этого компонента мы назовем краткосрочной альфа, и она представляет собой отклонения от ожидаемого приращения активов.
будет ненулевой и отклонения от ее долгосрочного или предсказуемого уровня быстро нивелируются. Такое поведение этого компонента мы назовем краткосрочной альфа, и она представляет собой отклонения от ожидаемого приращения активов.
Докажем, что является коинтеграционным фактором, продемонстрировав, что это, несомненно, процесс возврата к среднему. Во-первых отметим, что логарифмы цен удовлетворяют дифференциальному уравнению:
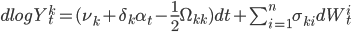 ,
,
которое мы используем для вычисления дифференциала :
\begin{equation}d\alpha_t=\sum_{k=1}^n a_k(\nu_k+\delta_k\alpha_t-\frac{1}{2}\Omega_{kk})dt+\sum_{k=1}^n a_k\sum_{i=1}^n\sigma_{ki}dW_t^i\end{equation}
Таким образом, мы можем записать компонент краткосрочной альфы как процесс возврата к среднему:

Здесь, оператор Tr() обозначает след матрицы, и А=diag(a) - диагональная матрица, чья диагональ состоит из а. Для уверенности, что модель действительно описывает процесс возврата к среднему, мы предположим, что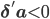 - и это мы увидим в результатах калибровки модели на реальных данных с биржи Nasdaq.
- и это мы увидим в результатах калибровки модели на реальных данных с биржи Nasdaq.
Рассматривая динамику (2), мы можем видеть, что возвращается к среднему с частотой, которая зависит от различной степени воздействия, какую оказывает на каждый актив (через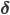 ), а также от силы вклада логарифма цены актива в саму
), а также от силы вклада логарифма цены актива в саму  (через а). Уровень возврата к среднему
(через а). Уровень возврата к среднему 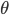 зависит от отношения волатильности к воздействию каждого компонента на общий дрифт активов и на дрифт каждого актива.
зависит от отношения волатильности к воздействию каждого компонента на общий дрифт активов и на дрифт каждого актива.
Альтернативное представление модели можно вывести, поместив выражение для непосредственно в дифференциальное уравнение для
непосредственно в дифференциальное уравнение для 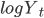 . В этом случае, мы получаем:
. В этом случае, мы получаем:
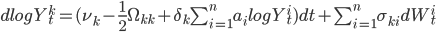 ,
,
и если мы обозначим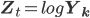 , где логарифм применен к каждому компоненту, то
, где логарифм применен к каждому компоненту, то
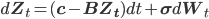 ,
,
где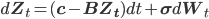 .
.
В этом представлении мы видим, что логарифм цены представляет собой векторно-авторегрессивную модель 1 порядка (VAR(1)). Отметим здесь, что B - вырожденная матрица. которая имеет одно положительное собственное значение, соответственно единственному фактору коинтеграции, который мы заложили в модель.
В следующей части мы найдем оптимальное динамическое уравнение распределения активов для нашего портфеля в закрытой форме, а затем продемонстрируем, как использовать выведенные формулы на практике, на примере портфеля из трех акций.
Задача оптимизации инвестиций
Целью трейдера при открытии позиций в активах является максимизация ожидания имеющихся ресурсов при постоянной ревизии этих позиций в течение времени, для того, чтобы обеспечить динамическую оптимальность стратегии. Обозначим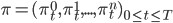 величину в денежном исчислении, инвестированную в безрисковый
величину в денежном исчислении, инвестированную в безрисковый 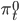 и рисковые активы
и рисковые активы 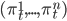 . Тогда количество открытых трейдером контрактов будет равно
. Тогда количество открытых трейдером контрактов будет равно 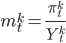 . Опустим сложный вывод конечной формулы и представим окончательное решение в закрытой форме для доли инвестиций в активы:
. Опустим сложный вывод конечной формулы и представим окончательное решение в закрытой форме для доли инвестиций в активы:
где - вектор оптимальных долей в используемых активах,
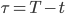 ,
,
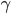 - мера риска (подбирается при тестировании).
- мера риска (подбирается при тестировании).
Первое слагаемое в приведенной формуле является классической мертоновской задачей, при том, что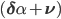 - дрифт цен активов. Второе слагаемое, пропорциональное а, представляет собой корректировку, связанную с коинтеграцией. Как показывает это выражение, преобразования в мертоновском портфеле уменьшаются при приближении конечного времени Т. В итоге, оптимальная стратегия зависит от , в общем случае оптимального инвестирования в несколько коинтегрированных активов.
- дрифт цен активов. Второе слагаемое, пропорциональное а, представляет собой корректировку, связанную с коинтеграцией. Как показывает это выражение, преобразования в мертоновском портфеле уменьшаются при приближении конечного времени Т. В итоге, оптимальная стратегия зависит от , в общем случае оптимального инвестирования в несколько коинтегрированных активов.
Эмпирическая производительность стратегии
В этом разделе мы продемонстрируем поведение стратегии в случае использования трех активов. Агент торгует портфелем из трех акций - GOOGL, FB, AMAZON, и мы используем реальные данные с биржи Nasdaq для определения параметров модели. Конкретно, мы используем средние цены книги заявок с периодичностью в одну минуту от 3 ноября 2014 года, для определения параметров VAR(1) модели логарифма цен в соответствии с регрессией:
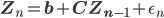 ,
,
где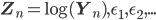 - независимые случайные переменные со стандартным нормальным распределением (с ковариационной матрицей
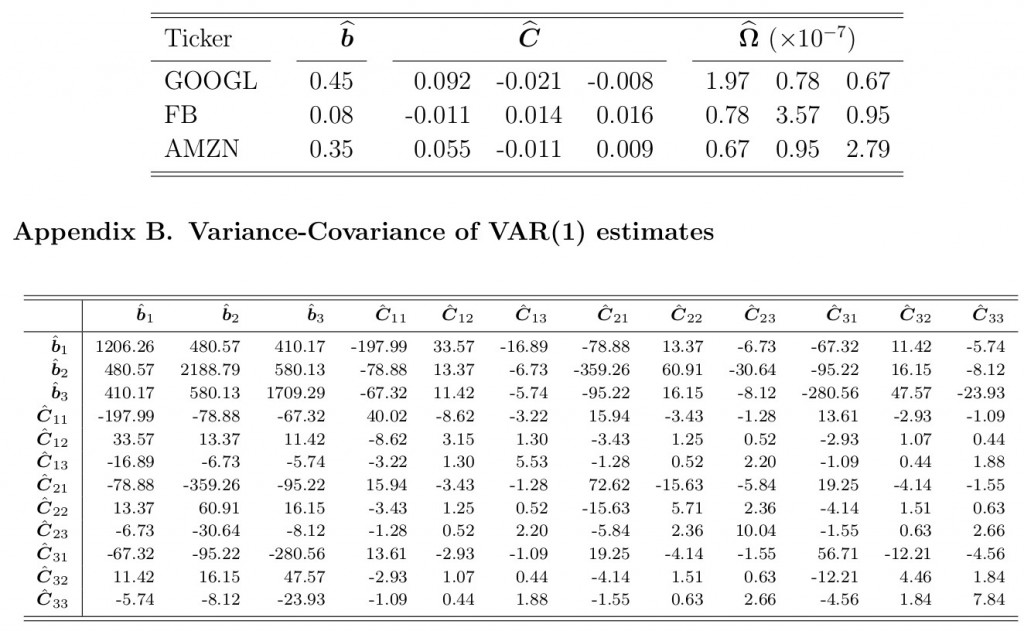
- независимые случайные переменные со стандартным нормальным распределением (с ковариационной матрицей 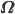 ) и 3х1 вектор b, и 3х3 матрица С , установленные из множественной регрессии. Из ошибок регрессии затем составляется дисперсионно-ковариационная матрица для . В таблицах ниже представлены результаты вычислений коэффициентов и дисперсионно-ковариационной матрицы.
) и 3х1 вектор b, и 3х3 матрица С , установленные из множественной регрессии. Из ошибок регрессии затем составляется дисперсионно-ковариационная матрица для . В таблицах ниже представлены результаты вычислений коэффициентов и дисперсионно-ковариационной матрицы.
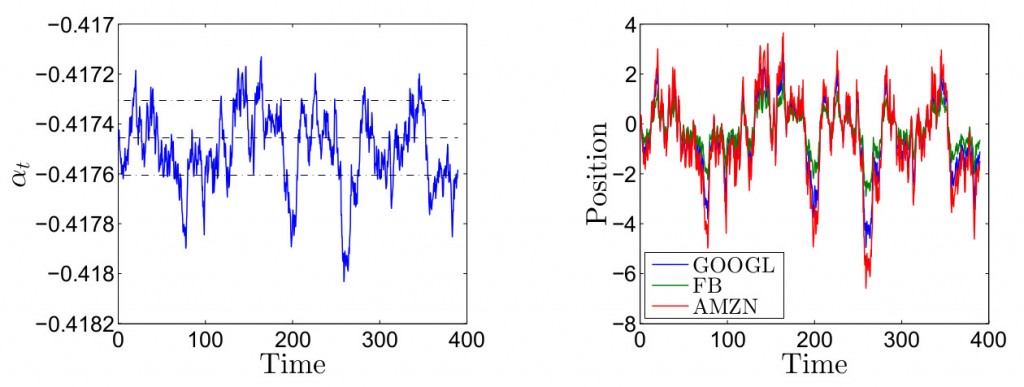
На рисунке ниже показано значение коинтеграционного фактора из тренировочной выборки, представляющего собой, как и ожидалось, процесс возврата к среднему. Прерывистая линия на рисунке показывает уровень возврата к среднему, плюс/минус два стандартных отклонения от коинтеграционного фактора вокруг уровня возврата к среднему (линии с точкой). Понятно, что краткосрочные отклонения от этого уровня являются основной причиной прибыльности стратегии, которую мы обсудим ниже.
из тренировочной выборки, представляющего собой, как и ожидалось, процесс возврата к среднему. Прерывистая линия на рисунке показывает уровень возврата к среднему, плюс/минус два стандартных отклонения от коинтеграционного фактора вокруг уровня возврата к среднему (линии с точкой). Понятно, что краткосрочные отклонения от этого уровня являются основной причиной прибыльности стратегии, которую мы обсудим ниже.
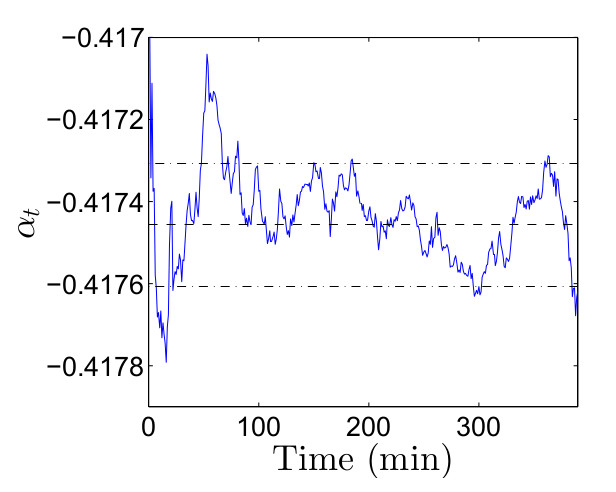
Далее, уменьшим размерность задачи до случая одного коинтеграционного фактора путем следующей последовательности трансформаций:
1. Определим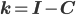 - матрица возврата к среднему, где
- матрица возврата к среднему, где 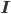 - единичная матрица.
- единичная матрица.
2. Определим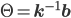 - уровень возврата к среднему
- уровень возврата к среднему
3. Диагонализируем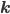 путем разложения
путем разложения 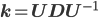 , где
, где 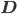 - матрица собственных значений, сортированных от наибольшего к наименьшему,
- матрица собственных значений, сортированных от наибольшего к наименьшему, 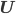 - матрица собственных значений, составленных постолбцово.
- матрица собственных значений, составленных постолбцово.
4. Определим матрицу с уменьшенной размерностью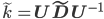 , где
, где 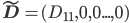 .
.
5. Затем установим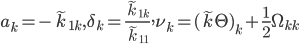 .
.
Результаты преобразований показаны в таблице ниже.
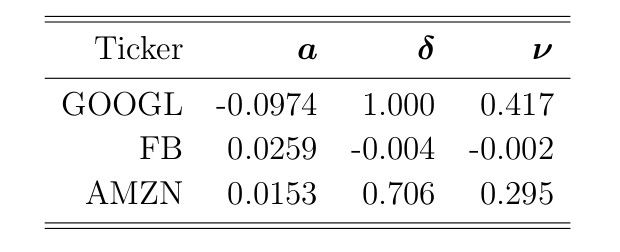
Отметим, что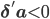 , значит процесс , несомненно, процесс возврата к среднему.
, значит процесс , несомненно, процесс возврата к среднему.
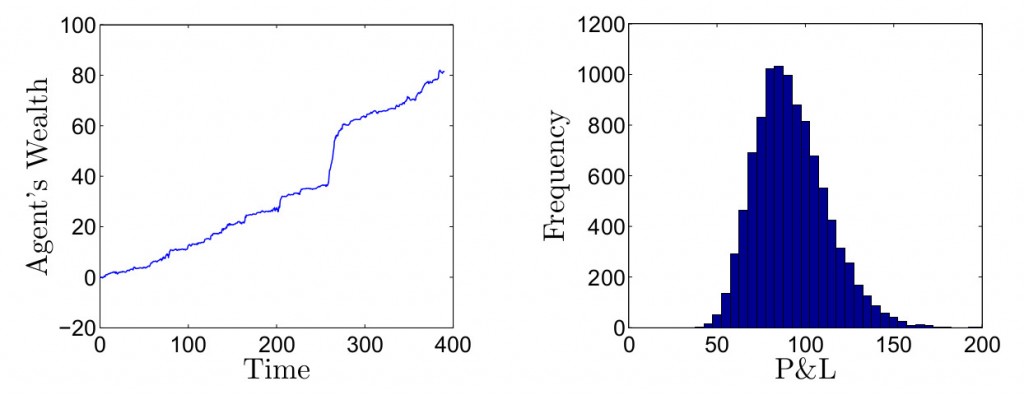
Для иллюстрации производительности стратегии мы произвели 10 000 симуляций и записали профиль P&L в каждом случае. Мы использовали установленные выше параметры для симуляции компонента краткосрочной альфы и графика коинтеграционной цены (для каждой минуты внутри торгового горизонта) для Google, Facebook и Amazon. Для каждого прохода мы предполагали, что агент начинает с нулевыми открытыми позициями в активах и все позиции ликвидируются в конце дня,все транзакции происходят по средней цене книги заявок и нет транзакционных издержек. На графиках в заглавии поста показан один из симуляционных путей и соответствующие ему оптимальные позиции в активах. На графиках ниже изображен процесс изменения ресурсов агента для данного пути и гистограмма прибыли/убытков для 10 000 проходов. Среднее значение прибыли составляет 91,99 и стандартное отклонение прибыли 20,27.
и соответствующие ему оптимальные позиции в активах. На графиках ниже изображен процесс изменения ресурсов агента для данного пути и гистограмма прибыли/убытков для 10 000 проходов. Среднее значение прибыли составляет 91,99 и стандартное отклонение прибыли 20,27.
Для данного конкретного прохода мы видим, что открытые позиции агента всегда находятся между 4 длинными и 6 короткими контрактами и прибыль в конце торгового периода составила приблизительно 80$. Открытые позиции активов демонстрируют паттерн, похожий на краткосрочную альфа прохода, оба показаны в заглавии поста. Помните, что включает дрифт каждого актива, так что во время, когда альфа выше уровня возврата к среднему соответствует моменту, где есть ожидание быстрого роста средних цен , то есть оптимальная стратегия - покупка актива.Соответственно, когда ниже уровня возрата к среднему - ожидание медленного роста цен (или даже их падения), где оптимально входить в короткие позиции по активам для получения краткосрочной прибыли от их снижения.
Заключение
Мы показали процесс оптимальной торговли набором коинтегрированных активов. Мы смоделировали структурную зависимость через общий компонент и дрифт приращений цен активов. Этот общий компонент является коинтеграционным фактором, который мы назвали краткосрочной альфа, и он является основным источником прибыльности в оптимальной инвестиционной стратегии.
Представляю здесь перевод этой статьи, которую я несколько сократил, убрав длинные математические выкладки и оставив только наиболее важные и окончательные формулировки. Думаю, это значительно облегчит понимание, без утраты основного смысла публикации.
Вступление
Успех многих торговых алгоритмов зависит от качества предсказаний движения цены актива. Предсказания цены отдельной акции в общем случае менее точно, чем предсказание значения портфеля активов. Классической стратегией, которая использует совместное поведение двух активов, является парный трейдинг, где портфель состоит из линейной комбинации этих активов. Для примера, это могут быть две акции, чей спред, представляющий собой разницу их цен, демонстрирует особый паттерн, отклонения от которого носят временный характер. Алгоритм парного трейдинга получает прибыль от ставки на тот факт, что отклонения спреда возвратятся к их историческому или предсказуемому уровню.
В данной работе мы создадим оптимальную стратегию, в которой агент открывает позиции в n коинтегрированных активах. Цель стратегии - получение прибыли от структурной зависимости в динамике их цен . Мы предполагаем, что активы коинтегрированы и создадим алгоритмическую торговую стратегию, где инвестор максимизирует ожидаемую функцию владения ( то есть вложенные и наличные средства). Мы выведем отдельную закрытую формулу для оптимальной (динамической) инвестиционной стратегии и покажем, что она учитывает коинтеграционный фактор. Далее, мы используем данные торгов с биржи Nasdaq для калибровки модели и проведем симуляцию, чтобы продемонстрировать, насколько стратегия производительна, в случае, когда инвестор открывает позиции в трех активах : Google, Facebook и Amazon.
Мы предполагаем, что дрифт в приращениях цен активов состоит из компонента, присущего только данному активу, и общего компонента для всех используемых активов. Общий компонент, который мы называем краткосрочной альфа, представляет собой процесс возврата к среднему с нулевым средним, являющийся естественным источником прибыли в торговой стратегии - он определяет прибыль от краткосрочных инвестиционных возможностей для коллекции активов.
Коинтегрированные логарифмы цен с краткосрочной альфа
Предположим, что дрифт в приращениях цен активов состоит из особого и общего компонентов. Особый компонент есть результат факторов, влияющих только на каждый отдельный актив, и общий компонент - результат индустриального или секторального набора факторов, которые влияют на всю коллекцию используемых активов. Таким образом, у нас есть коллекция активов, чей вектор цен обозначим
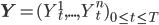 , который удовлетворяет системе дифференциальных уравнений:
, который удовлетворяет системе дифференциальных уравнений: \begin{equation}\frac{dY_t^k}{Y_t^k}=(\nu_k+\delta_k\alpha_t)dt+\sum_{i=1}^n\sigma_{ki}dW_t^i\end{equation}
где особый компонент
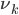 является константой, и общий компонент :
является константой, и общий компонент :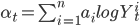
где
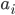 - константы, и
- константы, и 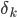 - специальная константа , которая показывает, как общий компонент влияет на каждый актив.
- специальная константа , которая показывает, как общий компонент влияет на каждый актив. 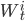 - стандартные Броуновские движения, независящие друг от друга, собранные в вектор
- стандартные Броуновские движения, независящие друг от друга, собранные в вектор 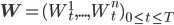 , и
, и 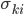 - неотрицательные константы. Мгновенную ковариацию между активами i и j можно определить как:
- неотрицательные константы. Мгновенную ковариацию между активами i и j можно определить как: 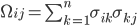 .
. Далее, обозначим
 матрицу, чьими элементами являются
матрицу, чьими элементами являются 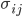 , представляющую собой разложение Холецкого мгновенной дисперсионно-ковариационной матрицы
, представляющую собой разложение Холецкого мгновенной дисперсионно-ковариационной матрицы 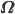 , таким образом
, таким образом 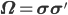 , где ' обозначает оператор транспонирования. Предположим, что нет дополнительных степеней свободы, так что
, где ' обозначает оператор транспонирования. Предположим, что нет дополнительных степеней свободы, так что  является обратимой.
является обратимой. Покажем, что
 ведет себя как фактор коинтеграции. Когда
ведет себя как фактор коинтеграции. Когда 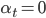 все активы являются геометрическими броуновскими движениями с дрифтом
все активы являются геометрическими броуновскими движениями с дрифтом 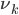 . В общем случае, на рынках акций,
. В общем случае, на рынках акций,  будет ненулевой и отклонения от ее долгосрочного или предсказуемого уровня быстро нивелируются. Такое поведение этого компонента мы назовем краткосрочной альфа, и она представляет собой отклонения от ожидаемого приращения активов.
будет ненулевой и отклонения от ее долгосрочного или предсказуемого уровня быстро нивелируются. Такое поведение этого компонента мы назовем краткосрочной альфа, и она представляет собой отклонения от ожидаемого приращения активов. Докажем, что является коинтеграционным фактором, продемонстрировав, что это, несомненно, процесс возврата к среднему. Во-первых отметим, что логарифмы цен удовлетворяют дифференциальному уравнению:
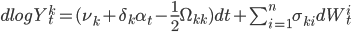 ,
, которое мы используем для вычисления дифференциала :
\begin{equation}d\alpha_t=\sum_{k=1}^n a_k(\nu_k+\delta_k\alpha_t-\frac{1}{2}\Omega_{kk})dt+\sum_{k=1}^n a_k\sum_{i=1}^n\sigma_{ki}dW_t^i\end{equation}
Таким образом, мы можем записать компонент краткосрочной альфы как процесс возврата к среднему:

Здесь, оператор Tr() обозначает след матрицы, и А=diag(a) - диагональная матрица, чья диагональ состоит из а. Для уверенности, что модель действительно описывает процесс возврата к среднему, мы предположим, что
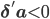 - и это мы увидим в результатах калибровки модели на реальных данных с биржи Nasdaq.
- и это мы увидим в результатах калибровки модели на реальных данных с биржи Nasdaq. Рассматривая динамику (2), мы можем видеть, что возвращается к среднему с частотой, которая зависит от различной степени воздействия, какую оказывает на каждый актив (через
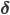 ), а также от силы вклада логарифма цены актива в саму
), а также от силы вклада логарифма цены актива в саму  (через а). Уровень возврата к среднему
(через а). Уровень возврата к среднему 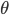 зависит от отношения волатильности к воздействию каждого компонента на общий дрифт активов и на дрифт каждого актива.
зависит от отношения волатильности к воздействию каждого компонента на общий дрифт активов и на дрифт каждого актива. Альтернативное представление модели можно вывести, поместив выражение для
 непосредственно в дифференциальное уравнение для
непосредственно в дифференциальное уравнение для 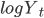 . В этом случае, мы получаем:
. В этом случае, мы получаем: 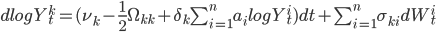 ,
, и если мы обозначим
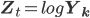 , где логарифм применен к каждому компоненту, то
, где логарифм применен к каждому компоненту, то 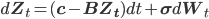 ,
, где
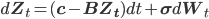 .
. В этом представлении мы видим, что логарифм цены представляет собой векторно-авторегрессивную модель 1 порядка (VAR(1)). Отметим здесь, что B - вырожденная матрица. которая имеет одно положительное собственное значение, соответственно единственному фактору коинтеграции, который мы заложили в модель.
В следующей части мы найдем оптимальное динамическое уравнение распределения активов для нашего портфеля в закрытой форме, а затем продемонстрируем, как использовать выведенные формулы на практике, на примере портфеля из трех акций.
Задача оптимизации инвестиций
Целью трейдера при открытии позиций в активах является максимизация ожидания имеющихся ресурсов при постоянной ревизии этих позиций в течение времени, для того, чтобы обеспечить динамическую оптимальность стратегии. Обозначим
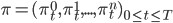 величину в денежном исчислении, инвестированную в безрисковый
величину в денежном исчислении, инвестированную в безрисковый 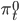 и рисковые активы
и рисковые активы 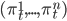 . Тогда количество открытых трейдером контрактов будет равно
. Тогда количество открытых трейдером контрактов будет равно 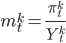 . Опустим сложный вывод конечной формулы и представим окончательное решение в закрытой форме для доли инвестиций в активы:
. Опустим сложный вывод конечной формулы и представим окончательное решение в закрытой форме для доли инвестиций в активы:где - вектор оптимальных долей в используемых активах,
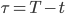 ,
, 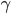 - мера риска (подбирается при тестировании).
- мера риска (подбирается при тестировании). Первое слагаемое в приведенной формуле является классической мертоновской задачей, при том, что
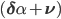 - дрифт цен активов. Второе слагаемое, пропорциональное а, представляет собой корректировку, связанную с коинтеграцией. Как показывает это выражение, преобразования в мертоновском портфеле уменьшаются при приближении конечного времени Т. В итоге, оптимальная стратегия зависит от , в общем случае оптимального инвестирования в несколько коинтегрированных активов.
- дрифт цен активов. Второе слагаемое, пропорциональное а, представляет собой корректировку, связанную с коинтеграцией. Как показывает это выражение, преобразования в мертоновском портфеле уменьшаются при приближении конечного времени Т. В итоге, оптимальная стратегия зависит от , в общем случае оптимального инвестирования в несколько коинтегрированных активов. Эмпирическая производительность стратегии
В этом разделе мы продемонстрируем поведение стратегии в случае использования трех активов. Агент торгует портфелем из трех акций - GOOGL, FB, AMAZON, и мы используем реальные данные с биржи Nasdaq для определения параметров модели. Конкретно, мы используем средние цены книги заявок с периодичностью в одну минуту от 3 ноября 2014 года, для определения параметров VAR(1) модели логарифма цен в соответствии с регрессией:
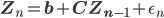 ,
, где
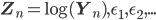 - независимые случайные переменные со стандартным нормальным распределением (с ковариационной матрицей
- независимые случайные переменные со стандартным нормальным распределением (с ковариационной матрицей 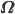 ) и 3х1 вектор b, и 3х3 матрица С , установленные из множественной регрессии. Из ошибок регрессии затем составляется дисперсионно-ковариационная матрица для . В таблицах ниже представлены результаты вычислений коэффициентов и дисперсионно-ковариационной матрицы.
) и 3х1 вектор b, и 3х3 матрица С , установленные из множественной регрессии. Из ошибок регрессии затем составляется дисперсионно-ковариационная матрица для . В таблицах ниже представлены результаты вычислений коэффициентов и дисперсионно-ковариационной матрицы. На рисунке ниже показано значение коинтеграционного фактора
 из тренировочной выборки, представляющего собой, как и ожидалось, процесс возврата к среднему. Прерывистая линия на рисунке показывает уровень возврата к среднему, плюс/минус два стандартных отклонения от коинтеграционного фактора вокруг уровня возврата к среднему (линии с точкой). Понятно, что краткосрочные отклонения от этого уровня являются основной причиной прибыльности стратегии, которую мы обсудим ниже.
из тренировочной выборки, представляющего собой, как и ожидалось, процесс возврата к среднему. Прерывистая линия на рисунке показывает уровень возврата к среднему, плюс/минус два стандартных отклонения от коинтеграционного фактора вокруг уровня возврата к среднему (линии с точкой). Понятно, что краткосрочные отклонения от этого уровня являются основной причиной прибыльности стратегии, которую мы обсудим ниже. 
Далее, уменьшим размерность задачи до случая одного коинтеграционного фактора путем следующей последовательности трансформаций:
1. Определим
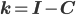 - матрица возврата к среднему, где
- матрица возврата к среднему, где 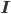 - единичная матрица.
- единичная матрица. 2. Определим
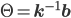 - уровень возврата к среднему
- уровень возврата к среднему 3. Диагонализируем
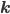 путем разложения
путем разложения 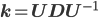 , где
, где 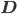 - матрица собственных значений, сортированных от наибольшего к наименьшему,
- матрица собственных значений, сортированных от наибольшего к наименьшему, 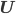 - матрица собственных значений, составленных постолбцово.
- матрица собственных значений, составленных постолбцово. 4. Определим матрицу с уменьшенной размерностью
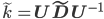 , где
, где 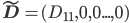 .
. 5. Затем установим
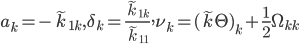 .
. Результаты преобразований показаны в таблице ниже.

Отметим, что
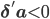 , значит процесс , несомненно, процесс возврата к среднему.
, значит процесс , несомненно, процесс возврата к среднему. Для иллюстрации производительности стратегии мы произвели 10 000 симуляций и записали профиль P&L в каждом случае. Мы использовали установленные выше параметры для симуляции компонента краткосрочной альфы и графика коинтеграционной цены (для каждой минуты внутри торгового горизонта) для Google, Facebook и Amazon. Для каждого прохода мы предполагали, что агент начинает с нулевыми открытыми позициями в активах и все позиции ликвидируются в конце дня,все транзакции происходят по средней цене книги заявок и нет транзакционных издержек. На графиках в заглавии поста показан один из симуляционных путей
 и соответствующие ему оптимальные позиции в активах. На графиках ниже изображен процесс изменения ресурсов агента для данного пути и гистограмма прибыли/убытков для 10 000 проходов. Среднее значение прибыли составляет 91,99 и стандартное отклонение прибыли 20,27.
и соответствующие ему оптимальные позиции в активах. На графиках ниже изображен процесс изменения ресурсов агента для данного пути и гистограмма прибыли/убытков для 10 000 проходов. Среднее значение прибыли составляет 91,99 и стандартное отклонение прибыли 20,27. Для данного конкретного прохода мы видим, что открытые позиции агента всегда находятся между 4 длинными и 6 короткими контрактами и прибыль в конце торгового периода составила приблизительно 80$. Открытые позиции активов демонстрируют паттерн, похожий на краткосрочную альфа прохода, оба показаны в заглавии поста. Помните, что включает дрифт каждого актива, так что во время, когда альфа выше уровня возврата к среднему соответствует моменту, где есть ожидание быстрого роста средних цен , то есть оптимальная стратегия - покупка актива.Соответственно, когда ниже уровня возрата к среднему - ожидание медленного роста цен (или даже их падения), где оптимально входить в короткие позиции по активам для получения краткосрочной прибыли от их снижения.
Заключение
Мы показали процесс оптимальной торговли набором коинтегрированных активов. Мы смоделировали структурную зависимость через общий компонент и дрифт приращений цен активов. Этот общий компонент является коинтеграционным фактором, который мы назвали краткосрочной альфа, и он является основным источником прибыльности в оптимальной инвестиционной стратегии.
Не является индивидуальной инвестиционной рекомендацией | При копировании ссылка обязательна | Нашли ошибку - выделить и нажать Ctrl+Enter | Жалоба