19 января 2016 QuantAlgos
Введение
Мы приводим явные формулы, также являющиеся и компьютерным кодом, по 101 сигналу для реальной торговли - так называемых альфа-сигналов. Среднее время удержания позиции по ним варьируется от 0.6 до 6.4 дней. Средняя величина парных корреляций этих сигналов довольно низкая, 15.9%. Прибыльность сильно коррелирует с волатильностью, но не имеет значительной зависимости от оборота, что напрямую подтверждает раннее полученный нами результат на основе косвенного эмпирического анализа. Также мы эмпирически установили, что оборачиваемость мало влияет на корреляцию альфа-сигналов.
Существуют две дополняющие друг друга – и в некотором смысле даже конкурирующие друг с другом - тенденции в современной алгоритмической торговле. С одной стороны, все больше и больше участников рынка (алготрейдеры, в частности) применяют сложные количественные методы для поиска альфа-сигналов, что приводит к появлению большого количества слабых и эфемерных сигналов. С другой стороны, технологические достижения позволяют существенно автоматизировать (большую часть) поискового процесса. Это дает все большее количество альф, чье число может составлять сотни тысяч и даже миллионы, и с экспоненциально возрастающим прогрессом в этой области, вероятно, достигнет и миллиарда... Такое распространение торговых сигналов – хотя, в большинстве своем, слабых и эфемерных – позволяет объединять их сложными математическими методами в единый “мега-альфа" сигнал. И тогда применяется именно этот “мега-альфа”, вместо торговли отдельными сигналами, что в качестве бонуса дает возможность автоматически сводить свои кросс-сделки внутри системы ( что имеет решающее значение для экономии на торговых издержках и т.п.), а также достичь диверсификации портфеля (добавляет возможности хеджирования), и так далее. Одной из проблем в совмещении альфа-сигналов обычно является ситуация “слишком много переменных, мало наблюдений”. Таким образом, ковариационная матрица альфа сигнала стремится к вырожденной.
Кроме того, алготрейдинг является довольно скрытной областью деятельности и по нему мало доступной информации. Это создает атмосферу загадочности вокруг современной алготорговли и порождает множество вопросов. Например, с таким большим количеством альфа-сигналов, имеется ли сильная корреляция между ними? Что из себя представляют эти сигналы? Основаны ли они на ценовых данных и данных по объему, на возврате к среднему, импульсах, и т. д.? Как прибыльность альфа-сигналов зависит от волатильности и оборотов ?
В предыдущей работе нами сделан шаг в демистификации области современной алготорговли при изучении некоторых эмпирических свойств 4,000 применяющихся в реальной торговле альфа-сигналов. В данной работе мы делаем еще один шаг и представляем явные формулы, также являющимися компьютерным кодом, для 101 альфа-сигнала. Эти шаблонные альфы – хотя большинство из них не так уж и просты – служат целью предоставить читателю краткий обзор того, что из себя представляют подобные сигналы. Это также позволит читателю повторить и проверить эти альфы на исторических данных и сделать новые исследования и эмпирический анализ. Надеюсь, в дальнейшем это вдохновит (молодых) исследователей на новые идеи и создание своих собственных альфа-сигналов.
Мы обсудим некоторые общие особенности наших шаблонных альф во 2 части статьи. Эти сигналы основаны на значениях “цена-объем” (дневная прибыль/убыток от закрытия предыдущего дня к закрытию текущего, открытие, закрытие, максимум, минимум, объем и средневзвешенная цена (vwap)), но в некоторых сигналах используется и “фундаментальный” вход, в том числе один сигнал использованием рыночной капитализации, а также ряд альф, применяющие некоторые типы бинарной промышленной классификации, такие как ОКВЭД, БИКС, НАИКС и др., которые используются для нейтрализации секторальных влияний.
Мы рассмотрим эмпирические свойства наших альф в части 3 на основе коэффициентов Шарпа для каждого сигнала, оборота и прибыльности в расчете на одну акцию, а также на ковариационной матрице выборки. Среднее время удержания позиции по сигналам колеблется примерно от 0,6 до 6,4 дней. Среднее (медиана) парной корреляции этих альф низкое, 15.9% (14.3%). Прибыль R сильно коррелирует с волатильностью V, и мы найдем эмпирическую зависимость:
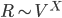
с X ≈ 0.76 для нашего 101 сигнала. Кроме того, мы покажем, что прибыль не имеет существенной зависимости от оборота Т.
Далее мы найдем эмпирически, что оборот как таковой плохо объясняет корреляцию альфа-сигналов. Точнее можно сказать, что попарная корреляция
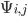сигналов (i, j = 1, ... , N, i ≠ j), не имеет сильной корреляции с произведением 
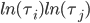, где 
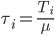и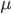 
- произвольная константа нормализации. Краткие выводы сделаем в части 4. Приложение А содержит наши формулы альфа-сигналов с определениями функций, операторов и используемых данных.
Формулы 101 альфа сигнала
В этом разделе мы опишем некоторые общие особенности наших 101 сигналов. Эти сигналы являются собственностью WorldQuant LLC и используются с его разрешения. Мы даем столько информации, насколько возможно в рамках ограничений, накладываемых правом собственности. Формулы выражений, которые также представляют собой компьютерный код – приведены в приложении А (в следующей части).
Очень приближенно можно сказать, что альфа-сигналы основаны либо на возврате к среднему, либо импульсе. Сигналы возврата к среднему имеют знак, противоположный приращению цены за период, лежащий в основе расчета. Пример простого сигнала возврата к среднему:
−ln(today`s open / yesterday`s close) (2)
Здесь в значении вчерашнего закрытия учтены любые сплиты и дивиденды, до момента текущей даты. Идея состоит в том, что значение цены актива вернется к среднему значению, чтобы вернуть часть прибыли (если сегодняшнее открытие выше вчерашнего закрытия) или возместить часть убытков (если сегодняшнее открытие ниже вчерашнего закрытия). Это так называемый сигнал с "задержкой-0". “Задержка-0” означает, что время определенных данных (например, цены), используемых в сигнале, совпадает со временем, в течение которого сигнал применяется для торговли. То есть, по сигналу (2) в идеале должны выставляться ордера в момент, или, более реалистично, максимально приближено к, сегодняшней цене открытия. В более широком смысле, это может быть какое-то другое время, например, закрытия дня.
Пример испульсного сигнала:
ln(yesterday′s close / yesterdayrs open) (3)
Здесь нет разницы, скорректированы цены (по дивидентам и сплитам) или нет. Идея заключается в том, что если цена актива возросла (снизилась) за вчерашний день, этот тренд продолжится сегодня и прибыль (убыток) будет и далее накапливаться. Это так называемый сигнал с “задержкой-1”, так как торговля будет происходить в текущий день (например, начиная с открытия). В общем, “задержка-1” означает, что сигнал торгуется на следующий день (период) после последних полученных данных. Сигналы с “задержкой-q” определяются по аналогии, где q - количество дней (периодов) после используемой для вычисления выборки.
В сложных сигналах элементы возврата к среднему и импульс могут быть смешаны, делая их менее разделимыми в этом отношении. Впрочем, можно разбить такие сигналы на малые составляющие, каждая из которых будет относиться к реверсии или импульсу. Например, альфа №101 в приложении А является импульсным сигналом с задержкой-1 : если актив внутри дня вырастает (то есть, close > open и high > low), на следующий день мы занимаем длинную позицию в этом активе. С другой стороны, альфа №42 в приложении А, по сути, реверсивный сигнал с "задержкой-0": величина rank(средневзвешенная цена(vwap) – close) снижается, если актив растет во второй половине дня (close > средневзвешенной цены (vwap)), наоборот - в случае снижения цены (close< средневзвешенной цены (vwap). Знаменатель нужен для снижения веса более дорогих активов. Вход в противоположную позицию осуществляется как можно более близко к закрытию дня.
Маркет дата и эмпирические свойства сигналов
Вычислим для наших сигналов, в годовом исчислении, дневной коэффициент Шарпа S, дневной оборот Т, и прибыльность на каждую акцию С. Обозначим наши альфы индексом i (i = 1, ... , n), где N = 101- количество сигналов. Для каждого сигнала определим
: 
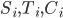где
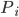-средняя дневная прибыль/убыток (в денежных единицах); 
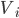- дневная волатильность портфеля; 
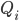- среднесуточный объем проданных+купленных акций для i-го сигнала; 
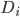- среднедневной объем торгов в деньгах; 
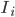- суммарные вложения в данный сигнал (фактически длинная плюс короткая позиция, без плечей). Принципиально, вложения
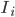являются постоянными; однако, 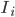колеблется из-за ежедневных прибылей/убытков. Таким образом, 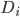и 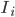изменяются совместно в уравнении (4). Период времени, в течение которого собирались данные - Дек 4, 2010 по Дек 31, 2013. Для этого же периода мы вычисляем ковариационную матрицу Yij полученных дневных прибылей для наших сигналов. Число наблюдений временного ряда составляет 1 006, и Yij является невырожденной. Из Yij мы вычисляем дневную волатильность
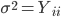и корреляционную матрицу 
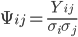(где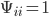 
). Заметим, что 
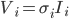, и средняя дневная прибыль равна 
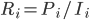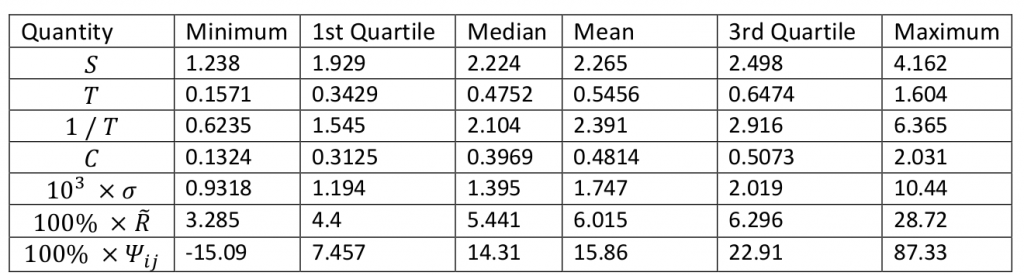
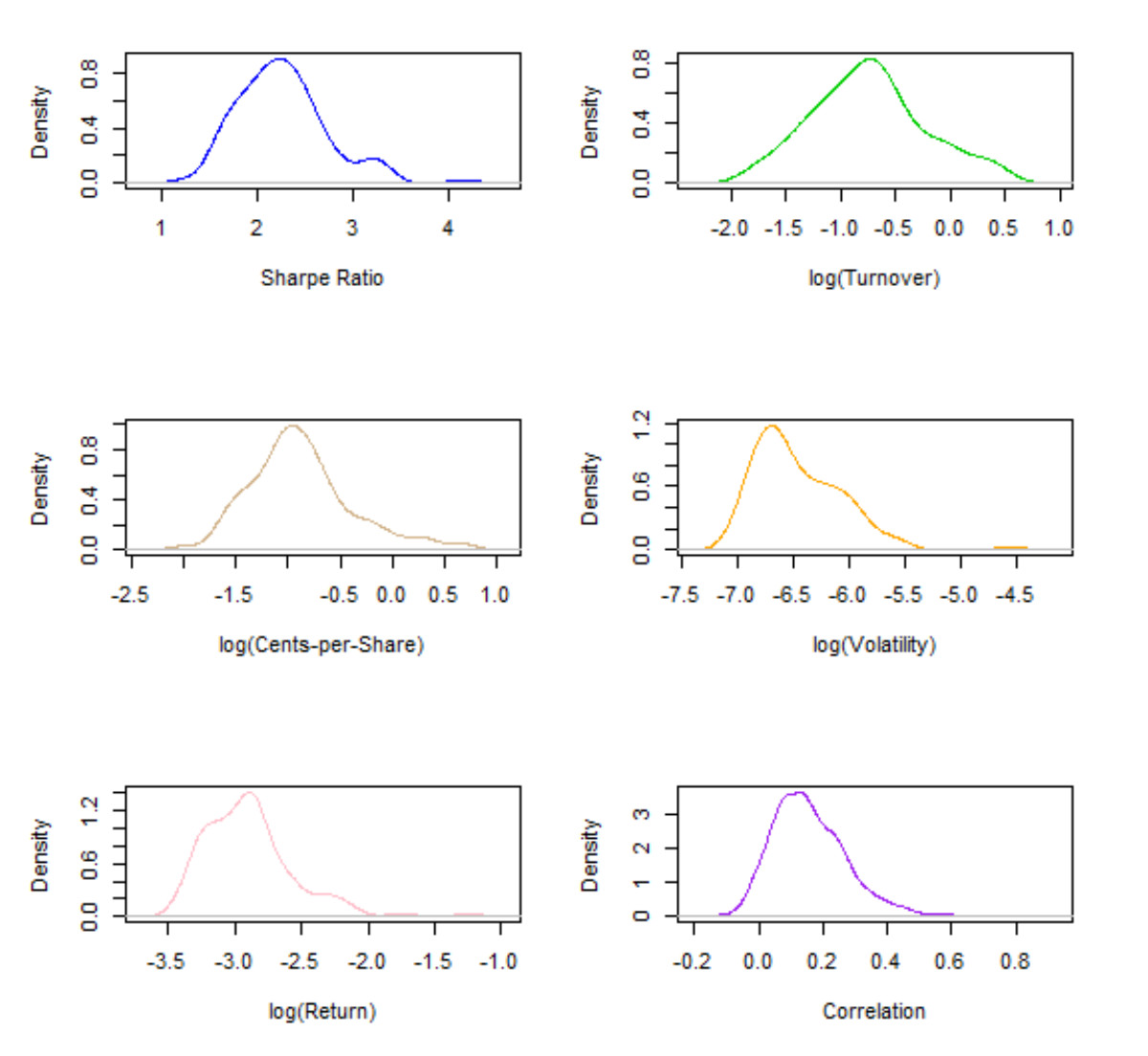
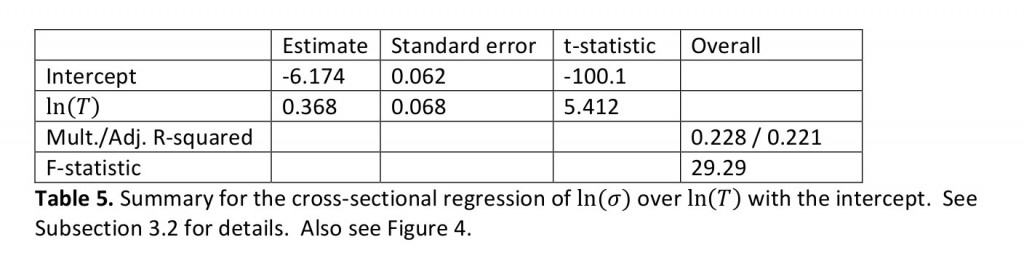
. Таблица в заглавии и рисунок ниже представляют данные для годового коэффициент Шарпа
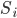, дневного оборота 
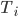, среднего периода владения 
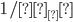, прибыльности на акцию 
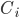, дневной волатильности прибыли 
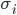, дневной прибыльности в годовом исчислени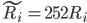и 
и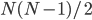 
попарных корреляций 
. 
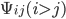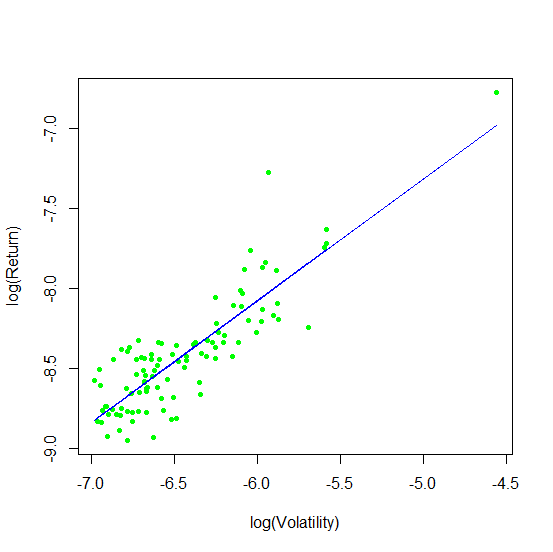
Зависимость прибыли от оборота и волатильности
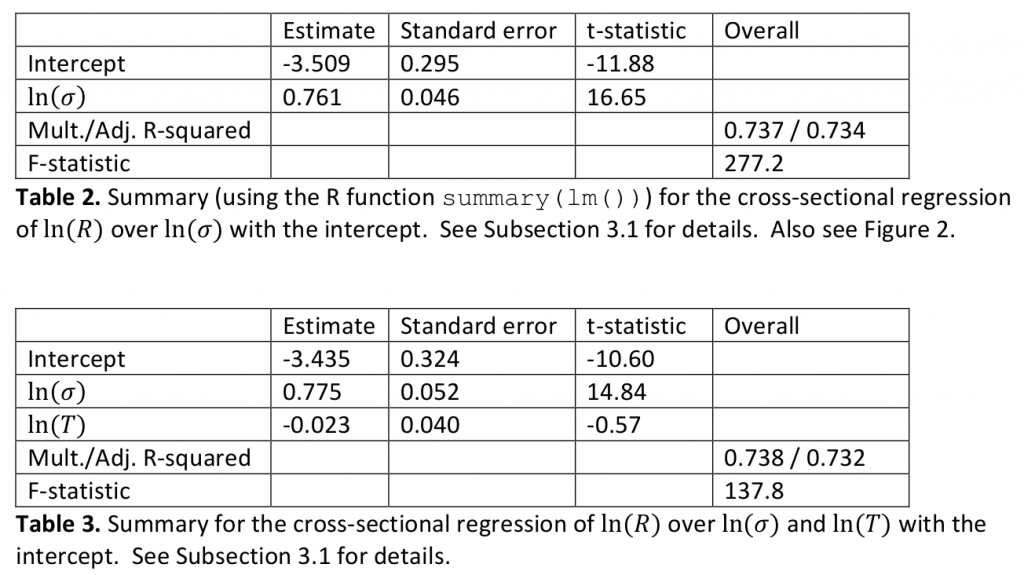
Мы построили две кросс-секционные зависимости
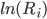от 1)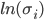 
в качестве единственной независимой переменной и 2) от 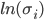и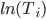 
. Результаты показаны в таблицах ниже. Согласно этим данным, у нас нет статистически значимой зависимости от оборотов 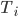, а средняя дневная прибыльность 
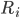сильно коррелирует с дневной волатильностью 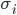с коэффициентом масштабирования (см. (1)) X ≈ 0.76.
Зависит ли корреляция сигналов от оборачиваемости?
Если мы проведем параллель между сигналами и акциями, то оборачиваемость по каждому альфа-сигналу является аналогом ликвидности акций, которая обычно измеряется через средний дневной объем торгов (ADDV). Логарифм ADDV обычно используется как фактор риска в многофакторных моделях для аппроксимации ковариации матричной структуры портфеля ценных бумаг, чье назначение заключается в моделировании вне-диагональных элементов ковариационной матрицы, то есть структуры парных корреляций. Следуя этой аналогии, мы можем задать вопрос, может ли оборачиваемость – или точнее ее логарифм – объяснить корреляции альфа-сигналов? Очевидно, что примененение оборачиваемости напрямую (в отличие от логарифма) ничего не даст из-за чрезвычайно искаженного (грубо логарифмически нормального) распределения оборота (см. рисунок в заглавии).
Чтобы ответить вопрос в заголовке, вспомним, что в факторной модели ковариационная матрица моделируется как:
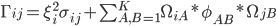
Здесь
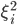- отдельная мера риска, 
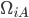- это матрица факторов размерностью NxK, соответствующая K<<N факторам, и 
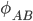- ковариационная матрица факторов. В нашем случае, мы заинтересованы в моделировании корреляционной матрицы 
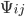, и в доказательствах, что оборачиваемость может объяснять попарную корреляцию. Отдельной темой также является корреляция между оборачиваемостью и волатильностью. Наш подход состоит в представлении одного из столбцов матрицы факторов, как
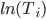. Точнее, заранее нет никакой причины, почему мы должны выбрать 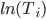в противоположность к 
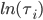, где 
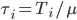, и 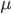- некоторый коэффициент нормализации. Чтобы разобраться с этим, нормализуем 
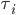так, что функция 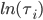будет иметь нулевую кросс-секционную среднюю , и пусть 
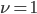будет единичным вектором. Затем мы можем построить три симметричных тензорных комбинации 
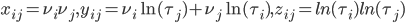. Cейчас определим сводный индекс 
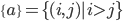, который принимает M = (N − 1)/2 значений, то есть мы преобразуем элементы нижнего треугольника основной симметричной матрицы 
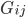в вектор 
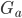. Таким образом мы можем создать четыре М-вектора 
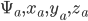. Тогда можно запустить линейную регрессию 
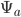по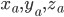 
. Отметим, что 
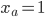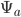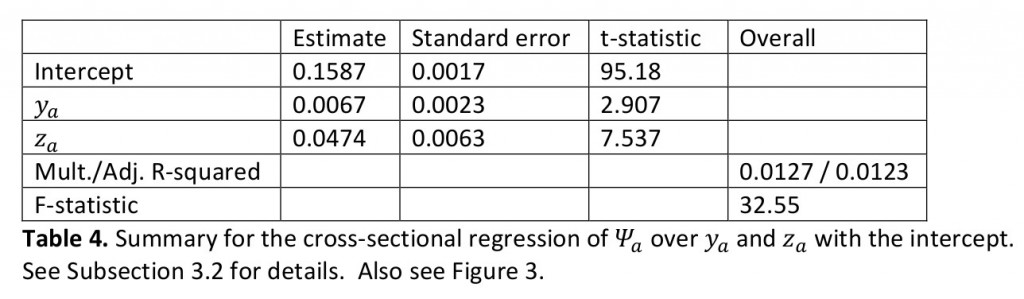
- просто единичный вектор, таким образом получается регрессия по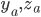 
со свободным членом. Результаты представлены в таблице ниже. Очевидно, что линейная и билинейная ( в 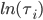) переменные 
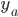и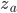 
имеют низкую объясняющую силу для попарных корреляций 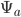, в то время как 
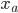просто моделирует среднюю корреляции 
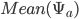. Помните, что конструкция 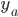и 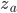ортогональна 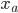, и все три переменных независимы друг от друга. 
Подчеркнем что наше заключение не обязательно означает, что оборачиваемость не добавляет значимости в контекст факторной модели, это означает только то, что оборот как таковой не участвует в моделировании парных корреляций альфа-сигналов. Приведенный выше анализ не учитывает, добавляет ли оборачиваемость объяснительную силу для моделирования дисперсии конкретного риска. Можно обнаружить,что линейная регрессия по (со свободным членом) показывает ненулевое значение корреляции между этими переменными (см. таблицу ниже), хотя и не очень большое. Чтобы увидеть, добавляет ли оборот что-то к значению, например, конкретного риска, требуется использование определенных методов, что выходит за рамки данной статьи.
Заключение.
Отметим, что 101 сигнал, который здесь мы приводим, не “игрушечные” альфы, а те, которые реально используются в торговле. На самом деле, 80 из этих сигналов участвуют в торговле на момент написания статьи. Насколько нам известно, это первый раз, когда такое большое количество реальных формул для торговых сигналов появляется в литературе. И это неудивительно, естественно, алгоритмическая торговля является весьма секретной и скрытной. Наша цель -предоставить возможность заглянуть в сложный мир современной и постоянно развивающейся алгоритмической торговли и демистифицировать его, в какой-то степени .
Технический прогресс сегодня позволяет автоматизировать поиск альфа-сигналов. Алгоритмические альфа-сигналы, безусловно, являются самыми многочисленными доступными торговыми сигналами, которые могут быть превращены в торговые стратегии. Существует множество перестановок в отдельных ( рыночно - нейтральных) портфелях, например, из 2 000 наиболее ликвидных американских акций, которые могут обеспечить положительную доходность на высоко - и среднечастотных временных горизонтах. Кроме того, многие из этих сигналов эфемерны и их обоснования слабы. Нужно делать сложные, технологически обоснованные и постоянно адаптируемые операции для поиска сотен тысяч и миллионов торговых сигналов, чтобы потом объединить их в единый “мега-альфа” сигнал, который будет торговаться с дополнительным бонусом по доходности за счет автоматического сведения внутренних кросс- сделок.
Приложение А: Формулы альфа-сигналов.
Alpha#1: (rank(Ts_ArgMax(SignedPower(((returns < 0) ? stddev(returns, 20) : close), 2.), 5)) -0.5)
Alpha#2: (-1 * correlation(rank(delta(log(volume), 2)), rank(((close - open) / open)), 6))
Alpha#3: (-1 * correlation(rank(open), rank(volume), 10))
Alpha#4: (-1 * Ts_Rank(rank(low), 9))
Alpha#5: (rank((open - (sum(vwap, 10) / 10))) * (-1 * abs(rank((close - vwap))))) Alpha#6: (-1 * correlation(open, volume, 10))
Alpha#7: ((adv20 < volume) ? ((-1 * ts_rank(abs(delta(close, 7)), 60)) * sign(delta(close, 7))) : (-1* 1))
Alpha#8: (-1 * rank(((sum(open, 5) * sum(returns, 5)) - delay((sum(open, 5) * sum(returns, 5)),10))))
Alpha#9: ((0 < ts_min(delta(close, 1), 5)) ? delta(close, 1) : ((ts_max(delta(close, 1), 5) < 0) ?
delta(close, 1) : (-1 * delta(close, 1))))
Alpha#10: rank(((0 < ts_min(delta(close, 1), 4)) ? delta(close, 1) : ((ts_max(delta(close, 1), 4) < 0) ? delta(close, 1) : (-1 * delta(close, 1)))))
Alpha#11: ((rank(ts_max((vwap - close), 3)) + rank(ts_min((vwap - close), 3))) * rank(delta(volume, 3)))
Alpha#12: (sign(delta(volume, 1)) * (-1 * delta(close, 1)))
Alpha#13: (-1 * rank(covariance(rank(close), rank(volume), 5)))
Alpha#14: ((-1 * rank(delta(returns, 3))) * correlation(open, volume, 10))
Alpha#15: (-1 * sum(rank(correlation(rank(high), rank(volume), 3)), 3))
Alpha#16: (-1 * rank(covariance(rank(high), rank(volume), 5)))
Alpha#17: (((-1 * rank(ts_rank(close, 10))) * rank(delta(delta(close, 1), 1))) * rank(ts_rank((volume / adv20), 5)))
Alpha#18: (-1 * rank(((stddev(abs((close - open)), 5) + (close - open)) + correlation(close, open, 10))))
Alpha#19: ((-1 * sign(((close - delay(close, 7)) + delta(close, 7)))) * (1 + rank((1 + sum(returns, 250)))))
Alpha#20: (((-1 * rank((open - delay(high, 1)))) * rank((open - delay(close, 1)))) * rank((open - delay(low, 1))))
Alpha#21: ((((sum(close, 8) / 8) + stddev(close, 8)) < (sum(close, 2) / 2)) ? (-1 * 1) : (((sum(close,2) / 2) < ((sum(close, 8) / 8) - stddev(close, 8))) ? 1 : (((1 < (volume / adv20)) || ((volume /adv20) == 1)) ? 1 : (-1 * 1))))
Alpha#22: (-1 * (delta(correlation(high, volume, 5), 5) * rank(stddev(close, 20))))
Alpha#23: (((sum(high, 20) / 20) < high) ? (-1 * delta(high, 2)) : 0)
Alpha#24: ((((delta((sum(close, 100) / 100), 100) / delay(close, 100)) < 0.05) || ((delta((sum(close, 100) / 100), 100) / delay(close, 100)) == 0.05)) ? (-1 * (close - ts_min(close,100))) : (-1 * delta(close, 3)))
Alpha#25: rank(((((-1 * returns) * adv20) * vwap) * (high - close)))
Alpha#26: (-1 * ts_max(correlation(ts_rank(volume, 5), ts_rank(high, 5), 5), 3))
Alpha#27: ((0.5 < rank((sum(correlation(rank(volume), rank(vwap), 6), 2) / 2.0))) ? (-1 * 1) : 1) Alpha#28: scale(((correlation(adv20, low, 5) + ((high + low) /2)) - close))
Alpha#29: (min(product(rank(rank(scale(log(sum(ts_min(rank(rank((-1 * rank(delta((close - 1), 5))))), 2), 1))))), 1), 5) + ts_rank(delay((-1 * returns), 6), 5))
Alpha#30: (((1.0 - rank(((sign((close - delay(close, 1))) + sign((delay(close, 1) - delay(close, 2)))) +sign((delay(close, 2) - delay(close, 3)))))) * sum(volume, 5)) / sum(volume, 20))
Alpha#31: ((rank(rank(rank(decay_linear((-1 * rank(rank(delta(close, 10)))), 10)))) + rank((-1 * delta(close, 3)))) + sign(scale(correlation(adv20, low, 12))))
Alpha#32: (scale(((sum(close, 7) / 7) - close)) + (20 * scale(correlation(vwap, delay(close, 5),230))))
Alpha#33: rank((-1 * ((1 - (open / close))^1)))
Alpha#34: rank(((1 - rank((stddev(returns, 2) / stddev(returns, 5)))) + (1 - rank(delta(close, 1)))))
Alpha#35: ((Ts_Rank(volume, 32) * (1 - Ts_Rank(((close + high) - low), 16))) * (1 - Ts_Rank(returns, 32)))
Alpha#36: (((((2.21 * rank(correlation((close - open), delay(volume, 1), 15))) + (0.7 * rank((open- close)))) + (0.73 * rank(Ts_Rank(delay((-1 * returns), 6), 5)))) + rank(abs(correlation(vwap, adv20, 6)))) + (0.6 * rank((((sum(close, 200) / 200) - open) * (close - open)))))
Alpha#37: (rank(correlation(delay((open - close), 1), close, 200)) + rank((open - close))) Alpha#38: ((-1 * rank(Ts_Rank(close, 10))) * rank((close / open)))
Alpha#39: ((-1 * rank((delta(close, 7) * (1 - rank(decay_linear((volume / adv20), 9)))))) * (1 +rank(sum(returns, 250))))
Alpha#40: ((-1 * rank(stddev(high, 10))) * correlation(high, volume, 10)) Alpha#41: (((high * low)^0.5) - vwap)
Alpha#42: (rank((vwap - close)) / rank((vwap + close)))
Alpha#43: (ts_rank((volume / adv20), 20) * ts_rank((-1 * delta(close, 7)), 8))
Alpha#44: (-1 * correlation(high, rank(volume), 5))
Alpha#45: (-1 * ((rank((sum(delay(close, 5), 20) / 20)) * correlation(close, volume, 2)) *rank(correlation(sum(close, 5), sum(close, 20), 2))))
Alpha#46: ((0.25 < (((delay(close, 20) - delay(close, 10)) / 10) - ((delay(close, 10) - close) / 10))) ?(-1 * 1) : (((((delay(close, 20) - delay(close, 10)) / 10) - ((delay(close, 10) - close) / 10)) < 0) ? 1 :((-1 * 1) * (close - delay(close, 1)))))
Alpha#47: ((((rank((1 / close)) * volume) / adv20) * ((high * rank((high - close))) / (sum(high, 5) / 5))) - rank((vwap - delay(vwap, 5))))
Alpha#48: (indneutralize(((correlation(delta(close, 1), delta(delay(close, 1), 1), 250) * delta(close, 1)) / close), IndClass.subindustry) / sum(((delta(close, 1) / delay(close, 1))^2), 250))
Alpha#49: (((((delay(close, 20) - delay(close, 10)) / 10) - ((delay(close, 10) - close) / 10)) < (-1 *0.1)) ? 1 : ((-1 * 1) * (close - delay(close, 1))))
Alpha#50: (-1 * ts_max(rank(correlation(rank(volume), rank(vwap), 5)), 5))
Alpha#51: (((((delay(close, 20) - delay(close, 10)) / 10) - ((delay(close, 10) - close) / 10)) < (-1 *0.05)) ? 1 : ((-1 * 1) * (close - delay(close, 1))))
Alpha#52: ((((-1 * ts_min(low, 5)) + delay(ts_min(low, 5), 5)) * rank(((sum(returns, 240) -sum(returns, 20)) / 220))) * ts_rank(volume, 5))
Alpha#53: (-1 * delta((((close - low) - (high - close)) / (close - low)), 9))
Alpha#54: ((-1 * ((low - close) * (open^5))) / ((low - high) * (close^5)))
Alpha#55: (-1 * correlation(rank(((close - ts_min(low, 12)) / (ts_max(high, 12) - ts_min(low, 12)))), rank(volume), 6))
Alpha#56: (0 - (1 * (rank((sum(returns, 10) / sum(sum(returns, 2), 3))) * rank((returns * cap)))))
Alpha#57: (0 - (1 * ((close - vwap) / decay_linear(rank(ts_argmax(close, 30)), 2))))
Alpha#58: (-1 * Ts_Rank(decay_linear(correlation(IndNeutralize(vwap, IndClass.sector), volume, 3.92795), 7.89291), 5.50322))
Alpha#59: (-1 * Ts_Rank(decay_linear(correlation(IndNeutralize(((vwap * 0.728317) + (vwap * (1 - 0.728317))), IndClass.industry), volume, 4.25197),
16.2289), 8.19648))
Alpha#60: (0 - (1 * ((2 * scale(rank(((((close - low) - (high - close)) / (high - low)) * volume)))) - scale(rank(ts_argmax(close, 10))))))
Alpha#61: (rank((vwap - ts_min(vwap, 16.1219))) < rank(correlation(vwap, adv180, 17.9282)))
Alpha#62: ((rank(correlation(vwap, sum(adv20, 22.4101), 9.91009)) < rank(((rank(open) + rank(open)) < (rank(((high + low) / 2)) + rank(high))))) * -1)
Alpha#63: ((rank(decay_linear(delta(IndNeutralize(close, IndClass.industry), 2.25164), 8.22237))- rank(decay_linear(correlation(((vwap * 0.318108) + (open * (1 - 0.318108))), sum(adv180, 37.2467), 13.557), 12.2883))) * -1)
Alpha#64: ((rank(correlation(sum(((open * 0.178404) + (low * (1 - 0.178404))), 12.7054),sum(adv120, 12.7054), 16.6208)) < rank(delta(((((high + low) / 2) * 0.178404) + (vwap * (1 -0.178404))), 3.69741))) * -1)
Alpha#65: ((rank(correlation(((open * 0.00817205) + (vwap * (1 - 0.00817205))), sum(adv60, 8.6911), 6.40374)) < rank((open - ts_min(open, 13.635)))) * -1)
Alpha#66: ((rank(decay_linear(delta(vwap, 3.51013), 7.23052)) + Ts_Rank(decay_linear(((((low* 0.96633) + (low * (1 - 0.96633))) - vwap) / (open - ((high + low) / 2))), 11.4157), 6.72611)) * -1)
Alpha#67: ((rank((high - ts_min(high, 2.14593)))^rank(correlation(IndNeutralize(vwap, IndClass.sector), IndNeutralize(adv20, IndClass.subindustry), 6.02936))) * -1)
Alpha#68: ((Ts_Rank(correlation(rank(high), rank(adv15), 8.91644), 13.9333) <rank(delta(((close * 0.518371) + (low * (1 - 0.518371))), 1.06157))) * -1)
Alpha#69: ((rank(ts_max(delta(IndNeutralize(vwap, IndClass.industry), 2.72412), 4.79344))^Ts_Rank(correlation(((close * 0.490655) + (vwap * (1 - 0.490655))), adv20, 4.92416),9.0615)) * -1)
Alpha#70: ((rank(delta(vwap, 1.29456))^Ts_Rank(correlation(IndNeutralize(close, IndClass.industry), adv50, 17.8256), 17.9171)) * -1)
Alpha#71: max(Ts_Rank(decay_linear(correlation(Ts_Rank(close, 3.43976), Ts_Rank(adv180, 12.0647), 18.0175), 4.20501), 15.6948), Ts_Rank(decay_linear((rank(((low + open) - (vwap +vwap)))^2), 16.4662), 4.4388))
Alpha#72: (rank(decay_linear(correlation(((high + low) / 2), adv40, 8.93345), 10.1519)) / rank(decay_linear(correlation(Ts_Rank(vwap, 3.72469), Ts_Rank(volume, 18.5188), 6.86671),2.95011)))
Alpha#73: (max(rank(decay_linear(delta(vwap, 4.72775), 2.91864)),Ts_Rank(decay_linear(((delta(((open * 0.147155) + (low * (1 - 0.147155))), 2.03608) / ((open *0.147155) + (low * (1 - 0.147155)))) * -1), 3.33829), 16.7411)) * -1)
Alpha#74: ((rank(correlation(close, sum(adv30, 37.4843), 15.1365)) <rank(correlation(rank(((high * 0.0261661) + (vwap * (1 - 0.0261661)))), rank(volume), 11.4791)))* -1)
Alpha#75: (rank(correlation(vwap, volume, 4.24304)) < rank(correlation(rank(low), rank(adv50), 12.4413)))
Alpha#76: (max(rank(decay_linear(delta(vwap, 1.24383), 11.8259)), Ts_Rank(decay_linear(Ts_Rank(correlation(IndNeutralize(low, IndClass.sector), adv81, 8.14941), 19.569), 17.1543), 19.383)) * -1)
Alpha#77: min(rank(decay_linear(((((high + low) / 2) + high) - (vwap + high)), 20.0451)), rank(decay_linear(correlation(((high + low) / 2), adv40, 3.1614), 5.64125)))
Alpha#78: (rank(correlation(sum(((low * 0.352233) + (vwap * (1 - 0.352233))), 19.7428),sum(adv40, 19.7428), 6.83313))^rank(correlation(rank(vwap), rank(volume), 5.77492)))
Alpha#79: (rank(delta(IndNeutralize(((close * 0.60733) + (open * (1 - 0.60733))), IndClass.sector), 1.23438)) < rank(correlation(Ts_Rank(vwap, 3.60973), Ts_Rank(adv150,9.18637), 14.6644)))
Alpha#80: ((rank(Sign(delta(IndNeutralize(((open * 0.868128) + (high * (1 - 0.868128))), IndClass.industry), 4.04545)))^Ts_Rank(correlation(high, adv10, 5.11456), 5.53756)) * -1)
Alpha#81: ((rank(Log(product(rank((rank(correlation(vwap, sum(adv10, 49.6054), 8.47743))^4)), 14.9655))) < rank(correlation(rank(vwap), rank(volume), 5.07914))) * -1)
Alpha#82: (min(rank(decay_linear(delta(open, 1.46063), 14.8717)), Ts_Rank(decay_linear(correlation(IndNeutralize(volume, IndClass.sector), ((open * 0.634196) + (open * (1 - 0.634196))), 17.4842), 6.92131), 13.4283)) * -1)
Alpha#83: ((rank(delay(((high - low) / (sum(close, 5) / 5)), 2)) * rank(rank(volume))) / (((high - low) / (sum(close, 5) / 5)) / (vwap - close)))
Alpha#84: SignedPower(Ts_Rank((vwap - ts_max(vwap, 15.3217)), 20.7127), delta(close, 4.96796))
Alpha#85: (rank(correlation(((high * 0.876703) + (close * (1 - 0.876703))), adv30, 9.61331))^rank(correlation(Ts_Rank(((high + low) / 2), 3.70596), Ts_Rank(volume, 10.1595),7.11408)))
Alpha#86: ((Ts_Rank(correlation(close, sum(adv20, 14.7444), 6.00049), 20.4195) < rank(((open+ close) - (vwap + open)))) * -1)
Alpha#87: (max(rank(decay_linear(delta(((close * 0.369701) + (vwap * (1 - 0.369701))), 1.91233), 2.65461)), Ts_Rank(decay_linear(abs(correlation(IndNeutralize(adv81,IndClass.industry), close, 13.4132)), 4.89768), 14.4535)) * -1)
Alpha#88: min(rank(decay_linear(((rank(open) + rank(low)) - (rank(high) + rank(close))), 8.06882)), Ts_Rank(decay_linear(correlation(Ts_Rank(close, 8.44728), Ts_Rank(adv60,20.6966), 8.01266), 6.65053), 2.61957))
Alpha#89: (Ts_Rank(decay_linear(correlation(((low * 0.967285) + (low * (1 - 0.967285))), adv10, 6.94279), 5.51607), 3.79744) - Ts_Rank(decay_linear(delta(IndNeutralize(vwap,IndClass.industry), 3.48158), 10.1466), 15.3012))
Alpha#90: ((rank((close - ts_max(close, 4.66719)))^Ts_Rank(correlation(IndNeutralize(adv40, IndClass.subindustry), low, 5.38375), 3.21856)) * -1)
Alpha#91: ((Ts_Rank(decay_linear(decay_linear(correlation(IndNeutralize(close, IndClass.industry), volume, 9.74928), 16.398), 3.83219), 4.8667) -
rank(decay_linear(correlation(vwap, adv30, 4.01303), 2.6809))) * -1)
Alpha#92: min(Ts_Rank(decay_linear(((((high + low) / 2) + close) < (low + open)), 14.7221), 18.8683), Ts_Rank(decay_linear(correlation(rank(low), rank(adv30), 7.58555), 6.94024),6.80584))
Alpha#93: (Ts_Rank(decay_linear(correlation(IndNeutralize(vwap, IndClass.industry), adv81, 17.4193), 19.848), 7.54455) / rank(decay_linear(delta(((close * 0.524434) + (vwap * (1 -0.524434))), 2.77377), 16.2664)))
Alpha#94: ((rank((vwap - ts_min(vwap, 11.5783)))^Ts_Rank(correlation(Ts_Rank(vwap, 19.6462), Ts_Rank(adv60, 4.02992), 18.0926), 2.70756)) * -1)
Alpha#95: (rank((open - ts_min(open, 12.4105))) < Ts_Rank((rank(correlation(sum(((high + low)/ 2), 19.1351), sum(adv40, 19.1351), 12.8742))^5), 11.7584))
Alpha#96: (max(Ts_Rank(decay_linear(correlation(rank(vwap), rank(volume), 3.83878), 4.16783), 8.38151), Ts_Rank(decay_linear(Ts_ArgMax(correlation(Ts_Rank(close, 7.45404),Ts_Rank(adv60, 4.13242), 3.65459), 12.6556), 14.0365), 13.4143)) * -1)
Alpha#97: ((rank(decay_linear(delta(IndNeutralize(((low * 0.721001) + (vwap * (1 - 0.721001))), IndClass.industry), 3.3705), 20.4523)) - Ts_Rank(decay_linear(Ts_Rank(correlation(Ts_Rank(low,7.87871), Ts_Rank(adv60, 17.255), 4.97547), 18.5925), 15.7152), 6.71659)) * -1)
Alpha#98: (rank(decay_linear(correlation(vwap, sum(adv5, 26.4719), 4.58418), 7.18088)) -rank(decay_linear(Ts_Rank(Ts_ArgMin(correlation(rank(open), rank(adv15), 20.8187), 8.62571),6.95668), 8.07206)))
Alpha#99: ((rank(correlation(sum(((high + low) / 2), 19.8975), sum(adv60, 19.8975), 8.8136)) ”, “<”, “==”, “||”, “x ? y : z”
rank(x) = кросс-секционный ранг
delay(x, d) = значение x d дней назад
correlation(x, y, d) = корреляция временных серий x и y за последние d дней
covariance(x, y, d) =ковариация временных серий x и y за последние d дней
scale(x, a) = масштабирование x таким образом,что sum(abs(x)) = a ( начальное значение a = 1)
delta(x, d) = сегодняшнее значение x минус значение x d дней назад
signedpower(x, a) = x^a
decay_linear(x, d) = взвешенная скользящая средняя за последние d дней с линейно снижающимися весами d, d – 1, …, 1 (сумма весов должна быть равна 1)
indneutralize(x, g) = x кросс-секционально нейтрализовано к группе g (субиндустрия, индустрия, секторы, и т.д.), то есть, x кросс-секционно не влиеяет на группу g
ts_{O}(x, d) = оператор O применен к временной серии за последние d дней; нецелое число дней d преобразуется к floor(d)
ts_min(x, d) = минимум временной серии за последние d дней
ts_max(x, d) =макисмум временной серии за последние d дней
ts_argmax(x, d) = в какой день происходит ts_max(x, d)
ts_argmin(x, d) =в какой день происходит ts_min(x, d)
ts_rank(x, d) = ранг временной серии за последние d дней
min(x, d) = ts_min(x, d)
max(x, d) = ts_max(x, d)
sum(x, d) = сумма временной серии за последние d дней
product(x, d) = произведение временной серии за последние d дней
stddev(x, d) = скользящее среднеквадратичное отклонение временной серии за последние d дней
А2. Входные данные
returns = дневное приращение цены от закрытия к закрытию
open, close, high, low, volume = стандартные определения для дневных цен и объемов
vwap = дневная взвешенная по объему цена
cap = рыночная капитализация
adv{d} = средний денежный объем за последние d дней
IndClass = основное определение для бинарной индустриальной классификации (ОКВЭД и т.п.) в indneutralize(x, IndClass.level), где level = сектор, индустрия, субиндустрия и т.д.
Множественные IndClass в одном и том же сигнале не относятся к одинаковой классификации по индустриям.
Alpha#1: (rank(Ts_ArgMax(SignedPower(((returns < 0) ? stddev(returns, 20) : close), 2.), 5)) -0.5)
Alpha#2: (-1 * correlation(rank(delta(log(volume), 2)), rank(((close - open) / open)), 6))
Alpha#3: (-1 * correlation(rank(open), rank(volume), 10))
Alpha#4: (-1 * Ts_Rank(rank(low), 9))
Alpha#5: (rank((open - (sum(vwap, 10) / 10))) * (-1 * abs(rank((close - vwap))))) Alpha#6: (-1 * correlation(open, volume, 10))
Alpha#7: ((adv20 < volume) ? ((-1 * ts_rank(abs(delta(close, 7)), 60)) * sign(delta(close, 7))) : (-1* 1))
Alpha#8: (-1 * rank(((sum(open, 5) * sum(returns, 5)) - delay((sum(open, 5) * sum(returns, 5)),10))))
Alpha#9: ((0 < ts_min(delta(close, 1), 5)) ? delta(close, 1) : ((ts_max(delta(close, 1), 5) < 0) ?
delta(close, 1) : (-1 * delta(close, 1))))
Alpha#10: rank(((0 < ts_min(delta(close, 1), 4)) ? delta(close, 1) : ((ts_max(delta(close, 1), 4) < 0) ? delta(close, 1) : (-1 * delta(close, 1)))))
Alpha#11: ((rank(ts_max((vwap - close), 3)) + rank(ts_min((vwap - close), 3))) * rank(delta(volume, 3)))
Alpha#12: (sign(delta(volume, 1)) * (-1 * delta(close, 1)))
Alpha#13: (-1 * rank(covariance(rank(close), rank(volume), 5)))
Alpha#14: ((-1 * rank(delta(returns, 3))) * correlation(open, volume, 10))
Alpha#15: (-1 * sum(rank(correlation(rank(high), rank(volume), 3)), 3))
Alpha#16: (-1 * rank(covariance(rank(high), rank(volume), 5)))
Alpha#17: (((-1 * rank(ts_rank(close, 10))) * rank(delta(delta(close, 1), 1))) * rank(ts_rank((volume / adv20), 5)))
Alpha#18: (-1 * rank(((stddev(abs((close - open)), 5) + (close - open)) + correlation(close, open, 10))))
Alpha#19: ((-1 * sign(((close - delay(close, 7)) + delta(close, 7)))) * (1 + rank((1 + sum(returns, 250)))))
Alpha#20: (((-1 * rank((open - delay(high, 1)))) * rank((open - delay(close, 1)))) * rank((open - delay(low, 1))))
Alpha#21: ((((sum(close, 8) / 8) + stddev(close, 8)) < (sum(close, 2) / 2)) ? (-1 * 1) : (((sum(close,2) / 2) < ((sum(close, 8) / 8) - stddev(close, 8))) ? 1 : (((1 < (volume / adv20)) || ((volume /adv20) == 1)) ? 1 : (-1 * 1))))
Alpha#22: (-1 * (delta(correlation(high, volume, 5), 5) * rank(stddev(close, 20))))
Alpha#23: (((sum(high, 20) / 20) < high) ? (-1 * delta(high, 2)) : 0)
Alpha#24: ((((delta((sum(close, 100) / 100), 100) / delay(close, 100)) < 0.05) || ((delta((sum(close, 100) / 100), 100) / delay(close, 100)) == 0.05)) ? (-1 * (close - ts_min(close,100))) : (-1 * delta(close, 3)))
Alpha#25: rank(((((-1 * returns) * adv20) * vwap) * (high - close)))
Alpha#26: (-1 * ts_max(correlation(ts_rank(volume, 5), ts_rank(high, 5), 5), 3))
Alpha#27: ((0.5 < rank((sum(correlation(rank(volume), rank(vwap), 6), 2) / 2.0))) ? (-1 * 1) : 1) Alpha#28: scale(((correlation(adv20, low, 5) + ((high + low) /2)) - close))
Alpha#29: (min(product(rank(rank(scale(log(sum(ts_min(rank(rank((-1 * rank(delta((close - 1), 5))))), 2), 1))))), 1), 5) + ts_rank(delay((-1 * returns), 6), 5))
Alpha#30: (((1.0 - rank(((sign((close - delay(close, 1))) + sign((delay(close, 1) - delay(close, 2)))) +sign((delay(close, 2) - delay(close, 3)))))) * sum(volume, 5)) / sum(volume, 20))
Alpha#31: ((rank(rank(rank(decay_linear((-1 * rank(rank(delta(close, 10)))), 10)))) + rank((-1 * delta(close, 3)))) + sign(scale(correlation(adv20, low, 12))))
Alpha#32: (scale(((sum(close, 7) / 7) - close)) + (20 * scale(correlation(vwap, delay(close, 5),230))))
Alpha#33: rank((-1 * ((1 - (open / close))^1)))
Alpha#34: rank(((1 - rank((stddev(returns, 2) / stddev(returns, 5)))) + (1 - rank(delta(close, 1)))))
Alpha#35: ((Ts_Rank(volume, 32) * (1 - Ts_Rank(((close + high) - low), 16))) * (1 - Ts_Rank(returns, 32)))
Alpha#36: (((((2.21 * rank(correlation((close - open), delay(volume, 1), 15))) + (0.7 * rank((open- close)))) + (0.73 * rank(Ts_Rank(delay((-1 * returns), 6), 5)))) + rank(abs(correlation(vwap, adv20, 6)))) + (0.6 * rank((((sum(close, 200) / 200) - open) * (close - open)))))
Alpha#37: (rank(correlation(delay((open - close), 1), close, 200)) + rank((open - close))) Alpha#38: ((-1 * rank(Ts_Rank(close, 10))) * rank((close / open)))
Alpha#39: ((-1 * rank((delta(close, 7) * (1 - rank(decay_linear((volume / adv20), 9)))))) * (1 +rank(sum(returns, 250))))
Alpha#40: ((-1 * rank(stddev(high, 10))) * correlation(high, volume, 10)) Alpha#41: (((high * low)^0.5) - vwap)
Alpha#42: (rank((vwap - close)) / rank((vwap + close)))
Alpha#43: (ts_rank((volume / adv20), 20) * ts_rank((-1 * delta(close, 7)), 8))
Alpha#44: (-1 * correlation(high, rank(volume), 5))
Alpha#45: (-1 * ((rank((sum(delay(close, 5), 20) / 20)) * correlation(close, volume, 2)) *rank(correlation(sum(close, 5), sum(close, 20), 2))))
Alpha#46: ((0.25 < (((delay(close, 20) - delay(close, 10)) / 10) - ((delay(close, 10) - close) / 10))) ?(-1 * 1) : (((((delay(close, 20) - delay(close, 10)) / 10) - ((delay(close, 10) - close) / 10)) < 0) ? 1 :((-1 * 1) * (close - delay(close, 1)))))
Alpha#47: ((((rank((1 / close)) * volume) / adv20) * ((high * rank((high - close))) / (sum(high, 5) / 5))) - rank((vwap - delay(vwap, 5))))
Alpha#48: (indneutralize(((correlation(delta(close, 1), delta(delay(close, 1), 1), 250) * delta(close, 1)) / close), IndClass.subindustry) / sum(((delta(close, 1) / delay(close, 1))^2), 250))
Alpha#49: (((((delay(close, 20) - delay(close, 10)) / 10) - ((delay(close, 10) - close) / 10)) < (-1 *0.1)) ? 1 : ((-1 * 1) * (close - delay(close, 1))))
Alpha#50: (-1 * ts_max(rank(correlation(rank(volume), rank(vwap), 5)), 5))
Alpha#51: (((((delay(close, 20) - delay(close, 10)) / 10) - ((delay(close, 10) - close) / 10)) < (-1 *0.05)) ? 1 : ((-1 * 1) * (close - delay(close, 1))))
Alpha#52: ((((-1 * ts_min(low, 5)) + delay(ts_min(low, 5), 5)) * rank(((sum(returns, 240) -sum(returns, 20)) / 220))) * ts_rank(volume, 5))
Alpha#53: (-1 * delta((((close - low) - (high - close)) / (close - low)), 9))
Alpha#54: ((-1 * ((low - close) * (open^5))) / ((low - high) * (close^5)))
Alpha#55: (-1 * correlation(rank(((close - ts_min(low, 12)) / (ts_max(high, 12) - ts_min(low, 12)))), rank(volume), 6))
Alpha#56: (0 - (1 * (rank((sum(returns, 10) / sum(sum(returns, 2), 3))) * rank((returns * cap)))))
Alpha#57: (0 - (1 * ((close - vwap) / decay_linear(rank(ts_argmax(close, 30)), 2))))
Alpha#58: (-1 * Ts_Rank(decay_linear(correlation(IndNeutralize(vwap, IndClass.sector), volume, 3.92795), 7.89291), 5.50322))
Alpha#59: (-1 * Ts_Rank(decay_linear(correlation(IndNeutralize(((vwap * 0.728317) + (vwap * (1 - 0.728317))), IndClass.industry), volume, 4.25197),
16.2289), 8.19648))
Alpha#60: (0 - (1 * ((2 * scale(rank(((((close - low) - (high - close)) / (high - low)) * volume)))) - scale(rank(ts_argmax(close, 10))))))
Alpha#61: (rank((vwap - ts_min(vwap, 16.1219))) < rank(correlation(vwap, adv180, 17.9282)))
Alpha#62: ((rank(correlation(vwap, sum(adv20, 22.4101), 9.91009)) < rank(((rank(open) + rank(open)) < (rank(((high + low) / 2)) + rank(high))))) * -1)
Alpha#63: ((rank(decay_linear(delta(IndNeutralize(close, IndClass.industry), 2.25164), 8.22237))- rank(decay_linear(correlation(((vwap * 0.318108) + (open * (1 - 0.318108))), sum(adv180, 37.2467), 13.557), 12.2883))) * -1)
Alpha#64: ((rank(correlation(sum(((open * 0.178404) + (low * (1 - 0.178404))), 12.7054),sum(adv120, 12.7054), 16.6208)) < rank(delta(((((high + low) / 2) * 0.178404) + (vwap * (1 -0.178404))), 3.69741))) * -1)
Alpha#65: ((rank(correlation(((open * 0.00817205) + (vwap * (1 - 0.00817205))), sum(adv60, 8.6911), 6.40374)) < rank((open - ts_min(open, 13.635)))) * -1)
Alpha#66: ((rank(decay_linear(delta(vwap, 3.51013), 7.23052)) + Ts_Rank(decay_linear(((((low* 0.96633) + (low * (1 - 0.96633))) - vwap) / (open - ((high + low) / 2))), 11.4157), 6.72611)) * -1)
Alpha#67: ((rank((high - ts_min(high, 2.14593)))^rank(correlation(IndNeutralize(vwap, IndClass.sector), IndNeutralize(adv20, IndClass.subindustry), 6.02936))) * -1)
Alpha#68: ((Ts_Rank(correlation(rank(high), rank(adv15), 8.91644), 13.9333) <rank(delta(((close * 0.518371) + (low * (1 - 0.518371))), 1.06157))) * -1)
Alpha#69: ((rank(ts_max(delta(IndNeutralize(vwap, IndClass.industry), 2.72412), 4.79344))^Ts_Rank(correlation(((close * 0.490655) + (vwap * (1 - 0.490655))), adv20, 4.92416),9.0615)) * -1)
Alpha#70: ((rank(delta(vwap, 1.29456))^Ts_Rank(correlation(IndNeutralize(close, IndClass.industry), adv50, 17.8256), 17.9171)) * -1)
Alpha#71: max(Ts_Rank(decay_linear(correlation(Ts_Rank(close, 3.43976), Ts_Rank(adv180, 12.0647), 18.0175), 4.20501), 15.6948), Ts_Rank(decay_linear((rank(((low + open) - (vwap +vwap)))^2), 16.4662), 4.4388))
Alpha#72: (rank(decay_linear(correlation(((high + low) / 2), adv40, 8.93345), 10.1519)) / rank(decay_linear(correlation(Ts_Rank(vwap, 3.72469), Ts_Rank(volume, 18.5188), 6.86671),2.95011)))
Alpha#73: (max(rank(decay_linear(delta(vwap, 4.72775), 2.91864)),Ts_Rank(decay_linear(((delta(((open * 0.147155) + (low * (1 - 0.147155))), 2.03608) / ((open *0.147155) + (low * (1 - 0.147155)))) * -1), 3.33829), 16.7411)) * -1)
Alpha#74: ((rank(correlation(close, sum(adv30, 37.4843), 15.1365)) <rank(correlation(rank(((high * 0.0261661) + (vwap * (1 - 0.0261661)))), rank(volume), 11.4791)))* -1)
Alpha#75: (rank(correlation(vwap, volume, 4.24304)) < rank(correlation(rank(low), rank(adv50), 12.4413)))
Alpha#76: (max(rank(decay_linear(delta(vwap, 1.24383), 11.8259)), Ts_Rank(decay_linear(Ts_Rank(correlation(IndNeutralize(low, IndClass.sector), adv81, 8.14941), 19.569), 17.1543), 19.383)) * -1)
Alpha#77: min(rank(decay_linear(((((high + low) / 2) + high) - (vwap + high)), 20.0451)), rank(decay_linear(correlation(((high + low) / 2), adv40, 3.1614), 5.64125)))
Alpha#78: (rank(correlation(sum(((low * 0.352233) + (vwap * (1 - 0.352233))), 19.7428),sum(adv40, 19.7428), 6.83313))^rank(correlation(rank(vwap), rank(volume), 5.77492)))
Alpha#79: (rank(delta(IndNeutralize(((close * 0.60733) + (open * (1 - 0.60733))), IndClass.sector), 1.23438)) < rank(correlation(Ts_Rank(vwap, 3.60973), Ts_Rank(adv150,9.18637), 14.6644)))
Alpha#80: ((rank(Sign(delta(IndNeutralize(((open * 0.868128) + (high * (1 - 0.868128))), IndClass.industry), 4.04545)))^Ts_Rank(correlation(high, adv10, 5.11456), 5.53756)) * -1)
Alpha#81: ((rank(Log(product(rank((rank(correlation(vwap, sum(adv10, 49.6054), 8.47743))^4)), 14.9655))) < rank(correlation(rank(vwap), rank(volume), 5.07914))) * -1)
Alpha#82: (min(rank(decay_linear(delta(open, 1.46063), 14.8717)), Ts_Rank(decay_linear(correlation(IndNeutralize(volume, IndClass.sector), ((open * 0.634196) + (open * (1 - 0.634196))), 17.4842), 6.92131), 13.4283)) * -1)
Alpha#83: ((rank(delay(((high - low) / (sum(close, 5) / 5)), 2)) * rank(rank(volume))) / (((high - low) / (sum(close, 5) / 5)) / (vwap - close)))
Alpha#84: SignedPower(Ts_Rank((vwap - ts_max(vwap, 15.3217)), 20.7127), delta(close, 4.96796))
Alpha#85: (rank(correlation(((high * 0.876703) + (close * (1 - 0.876703))), adv30, 9.61331))^rank(correlation(Ts_Rank(((high + low) / 2), 3.70596), Ts_Rank(volume, 10.1595),7.11408)))
Alpha#86: ((Ts_Rank(correlation(close, sum(adv20, 14.7444), 6.00049), 20.4195) < rank(((open+ close) - (vwap + open)))) * -1)
Alpha#87: (max(rank(decay_linear(delta(((close * 0.369701) + (vwap * (1 - 0.369701))), 1.91233), 2.65461)), Ts_Rank(decay_linear(abs(correlation(IndNeutralize(adv81,IndClass.industry), close, 13.4132)), 4.89768), 14.4535)) * -1)
Alpha#88: min(rank(decay_linear(((rank(open) + rank(low)) - (rank(high) + rank(close))), 8.06882)), Ts_Rank(decay_linear(correlation(Ts_Rank(close, 8.44728), Ts_Rank(adv60,20.6966), 8.01266), 6.65053), 2.61957))
Alpha#89: (Ts_Rank(decay_linear(correlation(((low * 0.967285) + (low * (1 - 0.967285))), adv10, 6.94279), 5.51607), 3.79744) - Ts_Rank(decay_linear(delta(IndNeutralize(vwap,IndClass.industry), 3.48158), 10.1466), 15.3012))
Alpha#90: ((rank((close - ts_max(close, 4.66719)))^Ts_Rank(correlation(IndNeutralize(adv40, IndClass.subindustry), low, 5.38375), 3.21856)) * -1)
Alpha#91: ((Ts_Rank(decay_linear(decay_linear(correlation(IndNeutralize(close, IndClass.industry), volume, 9.74928), 16.398), 3.83219), 4.8667) -
rank(decay_linear(correlation(vwap, adv30, 4.01303), 2.6809))) * -1)
Alpha#92: min(Ts_Rank(decay_linear(((((high + low) / 2) + close) < (low + open)), 14.7221), 18.8683), Ts_Rank(decay_linear(correlation(rank(low), rank(adv30), 7.58555), 6.94024),6.80584))
Alpha#93: (Ts_Rank(decay_linear(correlation(IndNeutralize(vwap, IndClass.industry), adv81, 17.4193), 19.848), 7.54455) / rank(decay_linear(delta(((close * 0.524434) + (vwap * (1 -0.524434))), 2.77377), 16.2664)))
Alpha#94: ((rank((vwap - ts_min(vwap, 11.5783)))^Ts_Rank(correlation(Ts_Rank(vwap, 19.6462), Ts_Rank(adv60, 4.02992), 18.0926), 2.70756)) * -1)
Alpha#95: (rank((open - ts_min(open, 12.4105))) < Ts_Rank((rank(correlation(sum(((high + low)/ 2), 19.1351), sum(adv40, 19.1351), 12.8742))^5), 11.7584))
Alpha#96: (max(Ts_Rank(decay_linear(correlation(rank(vwap), rank(volume), 3.83878), 4.16783), 8.38151), Ts_Rank(decay_linear(Ts_ArgMax(correlation(Ts_Rank(close, 7.45404),Ts_Rank(adv60, 4.13242), 3.65459), 12.6556), 14.0365), 13.4143)) * -1)
Alpha#97: ((rank(decay_linear(delta(IndNeutralize(((low * 0.721001) + (vwap * (1 - 0.721001))), IndClass.industry), 3.3705), 20.4523)) - Ts_Rank(decay_linear(Ts_Rank(correlation(Ts_Rank(low,7.87871), Ts_Rank(adv60, 17.255), 4.97547), 18.5925), 15.7152), 6.71659)) * -1)
Alpha#98: (rank(decay_linear(correlation(vwap, sum(adv5, 26.4719), 4.58418), 7.18088)) -rank(decay_linear(Ts_Rank(Ts_ArgMin(correlation(rank(open), rank(adv15), 20.8187), 8.62571),6.95668), 8.07206)))
Alpha#99: ((rank(correlation(sum(((high + low) / 2), 19.8975), sum(adv60, 19.8975), 8.8136)) ”, “<”, “==”, “||”, “x ? y : z”
rank(x) = кросс-секционный ранг
delay(x, d) = значение x d дней назад
correlation(x, y, d) = корреляция временных серий x и y за последние d дней
covariance(x, y, d) =ковариация временных серий x и y за последние d дней
scale(x, a) = масштабирование x таким образом,что sum(abs(x)) = a ( начальное значение a = 1)
delta(x, d) = сегодняшнее значение x минус значение x d дней назад
signedpower(x, a) = x^a
decay_linear(x, d) = взвешенная скользящая средняя за последние d дней с линейно снижающимися весами d, d – 1, …, 1 (сумма весов должна быть равна 1)
indneutralize(x, g) = x кросс-секционально нейтрализовано к группе g (субиндустрия, индустрия, секторы, и т.д.), то есть, x кросс-секционно не влиеяет на группу g
ts_{O}(x, d) = оператор O применен к временной серии за последние d дней; нецелое число дней d преобразуется к floor(d)
ts_min(x, d) = минимум временной серии за последние d дней
ts_max(x, d) =макисмум временной серии за последние d дней
ts_argmax(x, d) = в какой день происходит ts_max(x, d)
ts_argmin(x, d) =в какой день происходит ts_min(x, d)
ts_rank(x, d) = ранг временной серии за последние d дней
min(x, d) = ts_min(x, d)
max(x, d) = ts_max(x, d)
sum(x, d) = сумма временной серии за последние d дней
product(x, d) = произведение временной серии за последние d дней
stddev(x, d) = скользящее среднеквадратичное отклонение временной серии за последние d дней
А2. Входные данные
returns = дневное приращение цены от закрытия к закрытию
open, close, high, low, volume = стандартные определения для дневных цен и объемов
vwap = дневная взвешенная по объему цена
cap = рыночная капитализация
adv{d} = средний денежный объем за последние d дней
IndClass = основное определение для бинарной индустриальной классификации (ОКВЭД и т.п.) в indneutralize(x, IndClass.level), где level = сектор, индустрия, субиндустрия и т.д.
Множественные IndClass в одном и том же сигнале не относятся к одинаковой классификации по индустриям.
Не является индивидуальной инвестиционной рекомендацией | При копировании ссылка обязательна | Нашли ошибку - выделить и нажать Ctrl+Enter | Жалоба