1. В Основных направлениях денежно-кредитной политики на 2015-17гг. Банк России дал элегантный ответ на притязания правительства устанавливать цель по инфляции (и - сделать ее повыше, дабы профинансировать бюджетный стимул; забывая, правда, при этом что контрциклическая бюджетная политика всегда и везде, начиная от немецких нацистов, направивших на восстановление занятости в 1933-34гг. бюджетные средства, втрое превышавшие инвестиции в промышленность, и почти вдвое – военные расходы в тот же период [1, table 4.3], и кончая тоже уже ставшим историей «планом Обамы», срабатывала лишь как дополнение к смене правительств, внося свою лепту в рост делового настроя, связанный, главным образом, с политическими переменами). В сценариях ЦБ более высокая цель по инфляции, и, соответственно, смягчение денежной политики, приводит не к росту, а, наоборот, к замедлению динамики денежной массы. И, как следствие – к сокращению возможностей финансировать бюджетный дефицит за счет сеньоража, т.е. размещению части госдолга на балансе Банка России в виде залогов по операциям рефинансирования банков.
В порядке интеллектуальной разминки в начале рабочей недели (дело, правда, немного затянулось – среда, как известно, это уже «маленькая суббота») захотелось составить просветитьку на тему: насколько реальна такая парадоксальная инверсия («чем больше печатаем денег, тем меньшую долю реальных расходов правительства можем покрыть этой печатью»), и каков её механизм. Вероятно, всем известно «уравнение обмена» (оно же «количественная теория денег»), представляющее собой «четыреххвостку» вида
М – P = Y – V,
где M - денежная масса; P - уровень (индекс) цен; Y – реальный (т.е. в фиксированных ценах) ВВП; V – скорость обращения денег; для упрощения последующих выкладок все показатели записаны в логарифмах.
Данное уравнение выполняется всегда и везде, поскольку просто представляет собой тождество, определяющее скорость обращения денег (или обратную ей величину «монетизации ВВП» М – (Y + P)); в популярных рассуждениях часто исходят из представления, что скорость обращения денег представляет собой некую константу, выводя отсюда пропорциональную связь роста количества денег в обращении и цен. В действительности это предположение если и встречает эмпирическую поддержку, то только на долгосрочных интервалах и при достаточно высокой инфляции. Краткосрочно же связь инфляции с денежной эмиссией отсутствует, и динамика денежной массы никак не может служить опережающим индикатором в прогнозе инфляции, либо свидетельствовать о мягкости или жесткости политики по регулированию уровня цен.
2. Исторически первым исследованием, где рассматривалась возможность обратного влияния инфляции на количество обращающихся дензнаков, стала статья Фила Кейгана [2], где записанное выше уравнение «спроса на реальные денежные остатки» (М – P) было модифицировано примерно следующим образом
Mt – Pt = αt – ß (EtP t+1 – Pt),
где αt – все прочие факторы, влияющие на спрос на реальные денежные остатки, кроме ожидаемой инфляции (включая и физобъём транзакций/ВВП - Yt); ß> 0 - эластичность спроса на реальные деньги относительно ожидаемой инфляции; Et – оператор прогнозирования, так что (EtP t+1 – Pt) – инфляционное ожидание на ближайший период времени [t, t+1]. Легко видеть отсюда, что уровень цен Pt будет представлять собой средневзвешенное количества напечатанных (и не «поглощенных» прочими факторами, вроде расширения физобъёма операций) денег (Mt - αt) и ожидаемого уровня цен (EtP t+1) с весами (1 + ß) -1 и (1 + ß) -1 ß соответственно; ясно, что чем больше ß, тем меньше влияние на цены изменений денежной эмиссии, и тем больше влияние психологических факторов (ожиданий).
Сам Кейган предполагал инфляционные ожидания адаптивными, т.е. корректирующимися в зависимости от фактически наблюдаемой инфляции, примерно так
EtP t+1 – Pt = (1- γ) (Et-1P t - Pt-1) + γ (Pt - Pt-1),
где γ (от 0 до 1) – параметр, характеризующий уровень ригидности ожиданий. Отсюда, после подстановок сюда выражений для Pt и Pt-1 из предыдущий формулы, получаем (если я ничего не напутал, приводя подобные члены)
EtP t+1 = [(1- γ (1- γ ß) -1]Et-1P t + (1- γ ß) -1[(1+ γ) (Mt - αt) - (Mt-1 - αt-1)],
т.е. решение для ожидания уровня цен, выражающее их через начальные ожидания E0P1 с коэффициентом [(1- γ (1- γ ß) -1]t и денежную эмиссию в интервале [0, t]. (В презентациях модели Кейгана обычно используются гораздо более компактные дифференциальные уравнения, но я решил заменить их более громоздкими рекурсивными формулами, дабы не отпугивать и так малочисленного потенциального читателя).
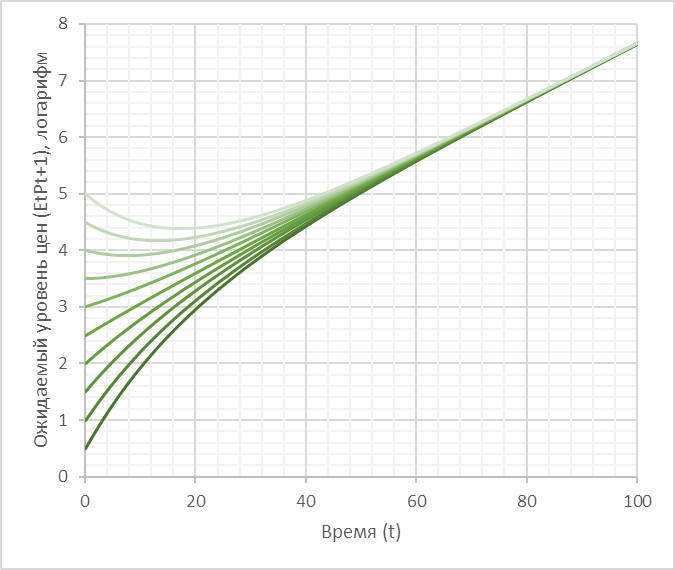
В случае, когда коэффициент [(1- γ (1- γß) -1] <1, т. е. γß < 1, ценовые ожидания представляют собой стационарный процесс, и влияние начальных ожиданий постепенно ослабевает. В этом случае ожидаемые и фактические уровни цен с течением времени будут все больше определяться денежной эмиссией, что проиллюстрировано на 2-х диаграммах выше. В противном случае (если реакция населения в виде «бегства от денег» на ожидания инфляции слишком острая, а сами ожидания достаточно гибко адаптируются к фактической инфляции) возможен «гиперинфляционный взрыв» без поддерживающей денежной эмиссии.
Пример показан на (3-ем) графике справа, который рассчитан при тех же темпах денежной эмиссии, что и первые два, но при более острой зависимости спроса на деньги от ожиданий их обесценения. Правда, сам Кейган, исследовав семь эпизодов гиперинфляции, ни в одном из них не нашел условий для возникновения самогенерирующийся или периодически колеблющейся инфляции - все они стали результатом безудержной денежной эмиссии в попытке профинансировать ей слишком большой бюджетный дефицит.
3. Из уравнения выше, определяющее спрос на реальные денежные остатки, ясно, что чем выше темп эмиссии, тем меньше будет этот спрос, выше скорость обращения денег, и, соответственно - ниже уровень «монетизации ВВП» (и стало быть, требования к ЦБ «догнать и перегнать Америку» по этому показателю, смягчив денежную политику и снизив ставки рефинансирования, абсурдно). Упрощенно (сильно упрощенно) предполагая, что кредит частному сектору отсутствует, а вся денежная масса обеспечена кредитом банковского сектора (ЦБ и коммерческих банков) правительству, получаем, что уровень монетизации ВВП в точности равен объему монетизированного (т.е. удерживаемого банковским сектором) госдолга (в отношении ВВП). Стало быть, возможности монетизации удельного (к ВВП) госдолга при более низкой эмиссии и инфляции, будут больше, на что и намекнул ЦБ в своих сценариях (см. иллюстрацию на графике справа).
Для объективности картины надо подчеркнуть, что показатели предельной монетизации бюджетного дефицита и монетизации госдолга все же имеют разную связь с динамикой эмиссии, поскольку госдолг быстрее обесценивается при более высокой эмиссии. В рамках рассмотренной выше адаптивной модели инфляционных ожиданий, вопрос о предельных размерах монетизации бюджетного дефицита (сеньоража) рассматривается в модели Бруно-Фишера. Согласно этой модели, в случае, когда превышение размером бюджетного дефицита темпа прироста ВВП достаточно мало, и позволяет профинансировать его с помощью эмиссии, устойчивым является равновесие с более низкими темпами инфляции.
4. Вариантом рассмотренной выше модели, когда скорость обращения денег зависит от их ожидаемого обесценения (инфляции), является предположение, что инфляционные ожидания зависят не от прошлых наблюдений (адаптивные ожидания), как в п.2, а от прогнозов в отношении эмиссионных планов правительства (денежных властей) в будущем (рациональные ожидания). В этом случае, подобно тому, как это происходит с уравнениями для цен акций [3], в решениях «уравнения обмена» появляются такие любопытные моменты, как «фундаментальные уровни цен» и «инфляционные пузыри».
Так, в предположении, что прогнозируемая эмиссия {Et (Mt+i - αt+i)}, i=1, ∞ растет не быстрее, чем с темпом 1+ ß -1, «уравнение обмена» с инфляционными ожиданиями имеет (вперед смотрящее) решение для уровня цен, являющееся аналогом фундаментальной составляющей для цен акций (опять-таки, если я не ошибся в подсчёте к-тов, ну – не важно)
Pt = (1+ ß) -1[(Mt - αt) + ∑i=1 ∞ (1+ ß -1)-i Et (Mt+i - αt+i)],
Фундаментальный уровень цен зависит в данной модели не только от текущего, но и от взвешенной суммы, ожидаемой будущего денежной эмиссии (за вычетом всех прочих факторов, определяющих спрос на реальные деньги кроме ожидаемой инфляции). Как в случае цен активов, инфляционный «пузырь» Bt, представляет собой решение гомогенного аналога «уравнения обмена» с инфляционными ожиданиями (т.е. при отсутствующей денежной эмиссии)
Bt = ß (EtBt+1 – Bt),
которое может быть записано как
Bt = (1+ ß -1)t + ∑i=1 ∞ (1+ ß -1)t-i zi,
где zt – инновация, т.е. новая информация, недоступная рынку ранее момента t (что формально означает Et-j zt = 0 для любого j≥1). Наличие положительного инфляционного пузыря в данной модели означает, что денежные активы недооценены и реальный спрос на них существенно ниже, чем это вытекает из текущих и ожидаемых объемов эмиссии.
Присутствие в качестве решений «мыльных инфляционных пузырей», основанных исключительно на самоподдерживающихся ожиданиях, позволяет иначе поставить вопрос о связи инфляции с денежной эмиссией, чем в исходной модели Кейгана. Была ли, например, Веймарская гиперинфляция 1923г. таким «мыльным пузырем»? Тесты, проведенные в [4], не смогли отвергнуть гипотезу, что инфляция в Германии не была пузырем, обусловленным паническим «бегством от рейхсмарки».
Однако проведенный в [5] анализ показал, что модель инфляции с рациональными ожиданиями обладает определенными противоречащими интуиции свойствами. При некоторых естественных ограничениях на ожидаемый рост денежного предложения (исключающих возникновение рациональных дефляционных пузырей), если рациональный инфляционный пузырь в этой модели и существует, то он, по-видимому, должен возникнуть сразу в момент начальной эмиссии денег. Более того, еще до этого агенты должны были предвидеть возникновение рационального инфляционного пузыря. После того, как такой пузырь лопнет, он не может перезапуститься. Тем не менее, модель не исключает существование рационального инфляционного пузыря, который уменьшается периодически, но никогда не взрывается.
Ссылки:
1. Werner Abelshauser (1998). «Germany: guns, butter, and economic miracles». In The economics of World War II: Six great powers in international comparison (ed. by Mark Harrison), Cambridge, UK, pp. 122-176.
2. Cagan, Phillip (1956). «The Monetary Dynamics of Hyperinflation». In Friedman, Milton (ed.). Studies in the Quantity Theory of Money. Chicago: University of Chicago Press.
3. Refet S. Gürkaynak (2005). Econometric Tests of Asset Price Bubbles: Taking Stock. Federal Reserve System, Washington.
4. Robert P. Flood and Peter M. Garber (1980). «Market Fundamentals versus Price-Level Bubbles: The First Tests». Journal of Political Economy. Vol. 88, No. 4 (Aug., 1980), pp. 745-770.
5. Diba, Behzad and Herschel Grossman (1987). «On the Inception of Rational Bubbles». Quarterly Journal of Economics. 87(August) pp.697-700.
1. Werner Abelshauser (1998). «Germany: guns, butter, and economic miracles». In The economics of World War II: Six great powers in international comparison (ed. by Mark Harrison), Cambridge, UK, pp. 122-176.
2. Cagan, Phillip (1956). «The Monetary Dynamics of Hyperinflation». In Friedman, Milton (ed.). Studies in the Quantity Theory of Money. Chicago: University of Chicago Press.
3. Refet S. Gürkaynak (2005). Econometric Tests of Asset Price Bubbles: Taking Stock. Federal Reserve System, Washington.
4. Robert P. Flood and Peter M. Garber (1980). «Market Fundamentals versus Price-Level Bubbles: The First Tests». Journal of Political Economy. Vol. 88, No. 4 (Aug., 1980), pp. 745-770.
5. Diba, Behzad and Herschel Grossman (1987). «On the Inception of Rational Bubbles». Quarterly Journal of Economics. 87(August) pp.697-700.
Доп. материалы и литература по гиперинфляции 1923г. в Германии: 1, 2.
Не является индивидуальной инвестиционной рекомендацией | При копировании ссылка обязательна | Нашли ошибку - выделить и нажать Ctrl+Enter | Жалоба




